基于马尔科夫链对BP神经网络法残差修正模型的短期风电功率预测

陈 娟，曹沁愉

(国网上海市电力公司青浦供电公司，上海 201799)

基于马尔科夫链对BP神经网络法残差修正模型的短期风电功率预测

陈 娟，曹沁愉

(国网上海市电力公司青浦供电公司，上海 201799)

风电功率预测对大规模风电并网运行有重要意义。建立基于马尔科夫链对BP神经网络法残差修正模型的短期风电功率预测，通过对训练样本的学习，利用BP神经网络法进行风电功率初步预测，同时得到了实测值与预测值的相对误差; 在此基础上利用马尔科夫链通过滚动预测对相对误差进行修正，有效地提高了预测结果的精度。并将该模型应用于某风电场的风电功率预测中，结果表明了此模型的可行性，并为风电功率预测提供了新的途径。

风电功率； BP神经网络；马尔科夫链； 短期预测

清洁替代和电能替代是能源发展的重要方向。清洁替代是指在能源开发上，以太阳能、风能、水能等清洁能源替代化石能源，从根本上解决人类能源供应面临的资源约束和环境约束的问题，实现能源可持续发展。风电，以其资源丰富、清洁无污染、实际占地少、可再生性等优势受到广泛关注。截至2016年，我国风电累计并网容量达1.49亿kW，占全部发电装机容量的9%，风电发电量为2410亿kWh，占全部发电量的4%。但是，风能作为一种不稳定的能源，具有随机性、间歇性和不可控性。随着风电的发展，风电场的穿透功率的不断加大，并网风电增加了电力系统调度计划制定的难度，因此对风电功率的精确预测具有重要的学术意义和现实价值。

被用于短期风电功率预测的方法主要有随机时间序列法、人工神经网络法、卡尔曼滤波法、支持向量机法等，以及各方法的不同组合。这些方法各有优缺点，随机时间序列法所需历史数据少但是预测周期短且所用数据单一无法形成合理的误差估计，对突变信息无法识别；卡尔曼滤波法能较好地捕捉到风电功率的变化规律且能不断更新状态信息，获得比较准确的预测结果但是不适用于波动性及其剧烈的情况；支持向量机法需要的数据少、有较强的非线性学习能力、训练时间短、泛化能力强、有效克服维数灾难和局部极小问题但是精度受所选核函数结构影响较大，对于核函数的准确性和完善性要求较高；而组合预测能够充分利用各单一方法数据信息，减少较大误差点，预测精度高。

文献[1]介绍的BP人工神经网络法能准确描述输入值和输出目标之间的映射关系，能够以任意精度逼近任何非线性映射；可以学习和自适应未知信息；具有分布式信息存储与处理结构；具有一定的容错性，因此构造出来的系统具有较好的鲁棒性，已被广泛应用于风电功率预测中。马尔科夫链(Markov Chain,MC)是研究系统状态转移规律的理论，自 20 世纪初俄国数学家马尔科夫(Markov)提出以来，在交通、生态、水文、地质等众多领域得到应用，取得了丰富的成果。但是在风电功率预测领域，涉及马尔科夫链的研究应用基本为空白。马尔科夫链是时间和状态都离散的Markov过程[2]。由于MC不受过去状态的影响，对于受多种因素影响的时间序列预测具有一定的优越性。本文提出基于BP神经网络法和马尔科夫链组合预测的方法，将历史风速及历史功率作为影响因素，建立风电功率预测模型。其技术路线为先将历史风速和历史功率数据输入至BP神经网络进行训练，训练完毕后将其输出功率和实际功率所得的相对误差通过马尔科夫链进行修正，然后将神经网络所得的输出功率与误差修正值进行结合，得到最终的预测结果。本文对我国某风电场的实际数据进行了预测，并与神经网络预测模型进行了比较，验证了本文方法的有效性。

1 BP神经网络模型

传统的BP神经网络模型预测步骤如下：

(1)神经网络初始化。根据实际需求确定网络输入层、隐含层、输出层的节点数分别为n，l，m，给出输入层和隐含层间的初始权值wij和初始阈值bj以及隐含层和输出层间的初始权值wjk和初始阈值bm，并设置初始学习速率η、终止误差e及最大迭代次数λ。

(2)信号的正向传递。 隐含层第j个 神经元的输出：

(1)

式中f——隐含层的激励函数，隐层神经元映射函数常采用 Sigmoid函数；xi——第i个输入节点的输入值。

输出层第k个神经元的输出：

(2)

式中f——输出层的激励函数，一般为Purelin函数。

学习误差函数：

(3)

式中yk——样本的实际输出。

(3)误差反向传播与权值阈值训练及更新。从隐含层第j个神经元到输出层第k个神经元的连接权值有如下更新增量计算公式：

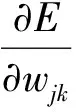
(4)

同理可得阈值更新增量：

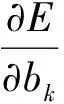
(5)

对输入层第i个神经元至隐含层第j个神经元之间的连接权值及阈值的更新增量的计算公式：

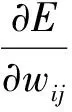
(6)

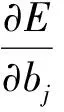
(7)

根据求得的各层神经元连接权值及阈值的变化增量来迭代更新用于下一轮的网络学习与训练的神经元连接权值及阈值，即：

wij(t+1)=wij(t)+Δwij(t)

(8)

wjk(t+1)=wjk(t)+Δwjk(t)

(9)

bj(t+1)=bj(t)+Δbj(t)

(10)

bk(t+1)=bk(t)+Δbk(t)

(11)

(4)判断学习是否结束。若误差小于等于e或迭代次数达到指定值λ，则学习结束并输出学习样本的预测值及预测值和实际值之间的相对误差APE。

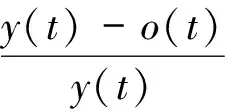
(12)

反之返回至步骤3继续训练。

2 MC对BP神经网络法的残差修正模型

MC是一种特殊的随机过程(马尔科夫过程),其可以根据系统当前时刻的状态推求下一时刻的状态概率分布,进而得到下一时刻的状态。其基本原理是:按照某个系统的发展,时间可离散为N=1,2,…，对每个系统的状态可用随机变量表示,并且对应一定的概率,称为状态概率，当马尔科夫过程由某一时刻状态转移到另一时刻状态时,在这个转移过程中存在着概率的转移,称为转移概率[3]。

预测数据与实际数据的差值称为残差，本文利用相对误差序列进行研究。记BP神经网络法训练所得的残差序列

ε={ε(1)，ε(2)，ε(3)，…，ε(n)}

(13)

分别求其均值与均方差值S：

(14)

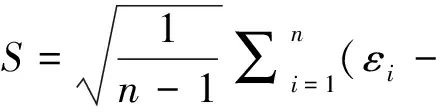
(15)

具体模型建立步骤如下：

(1)划分样本空间状态。经过马氏性检验后，求得样本序列最大值max{ε}以及最小值min{ε}，以及序列长度d=max-min，先将其状态空间根据最值均方差法划分为n(n=EVEN(d/S))个预定相对误差状态，即S=[S1，S2，…，Sn]。

(2)建立状态转移概率矩阵。基本状态转移概率矩阵为：

(16)

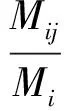
(17)

式中Pij——相对误差从第一预定相对误差状态Si经1个步长转移到第二预定相对误差状态Sj的概率；Mij——第一预定相对误差状态Si经过1个步长转移到第二预定相对误差状态Sj的次数；Mi——相对误差处于第一相对误差状态Si的个数。

那么，经k时步的转移概率矩阵P(k)为基本转移概率矩阵的次方，即：

P(k)=Pk

(18)

(3)残差修正。首先选取计算相对误差状态的实测相对误差状态组；其中，实测相对误差状态组是由计算相对误差状态的前m个(m阶)计算相对误差状态按照时间先后顺序组成。

m阶各自所占的权重ωk：

(19)

(20)

将这m阶的转移矩阵中的每个统一状态的概率按式(21)作加权和，得出的加权和最大的概率所处的预定相对误差状态记为待预测时步的计算相对误差状态，也称为预测状态。得到的此计算相对误差状态又可作为下一步的计算相对误差状态的实测相对误差状态组的元素之一，以此类推，进行滚动预测。

(21)

马尔科夫链预测是一个区间预测，得到了计算相对误差状态，即确定了残差的变化范围，但是在有些实际模型应用中需要精确预测，那么就需要马尔科夫链的点值预测，本模型取值为状态区间的中间值，则残差的修正值为

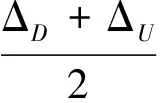
(22)

式中 ΔD，ΔU——计算相对误差状态对应的残差区间的下限值和上限值；f(x)——BP神经网络的输出功率的初始预测值。

具体计算流程图见图1所示。

图1 BP_MC预测模型流程图

3 实例验证

本论文研究对象为我国黑龙江某风电场某月份共31天现场数据， 额定容量为90.3 MW，每10 min采样一次，共计4 464组数据，其中4 320组数据作为训练样本， 144组数据作为测试样本。根据实际情况确定BP神经网络输入层的节点数为4、隐含层节点数为12、输出层节点为1；隐含层采用传递函数logsig函数，输出层采用传递函数purelin函数，学习速率采用0.05，最大训练次数为1 000，训练目标为0.001。

日风电功率序列点预测结果见图2～图4。

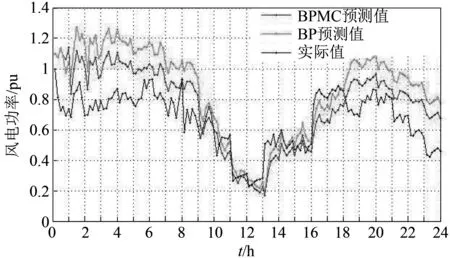
图2 BPMC模型24小时预测效果图

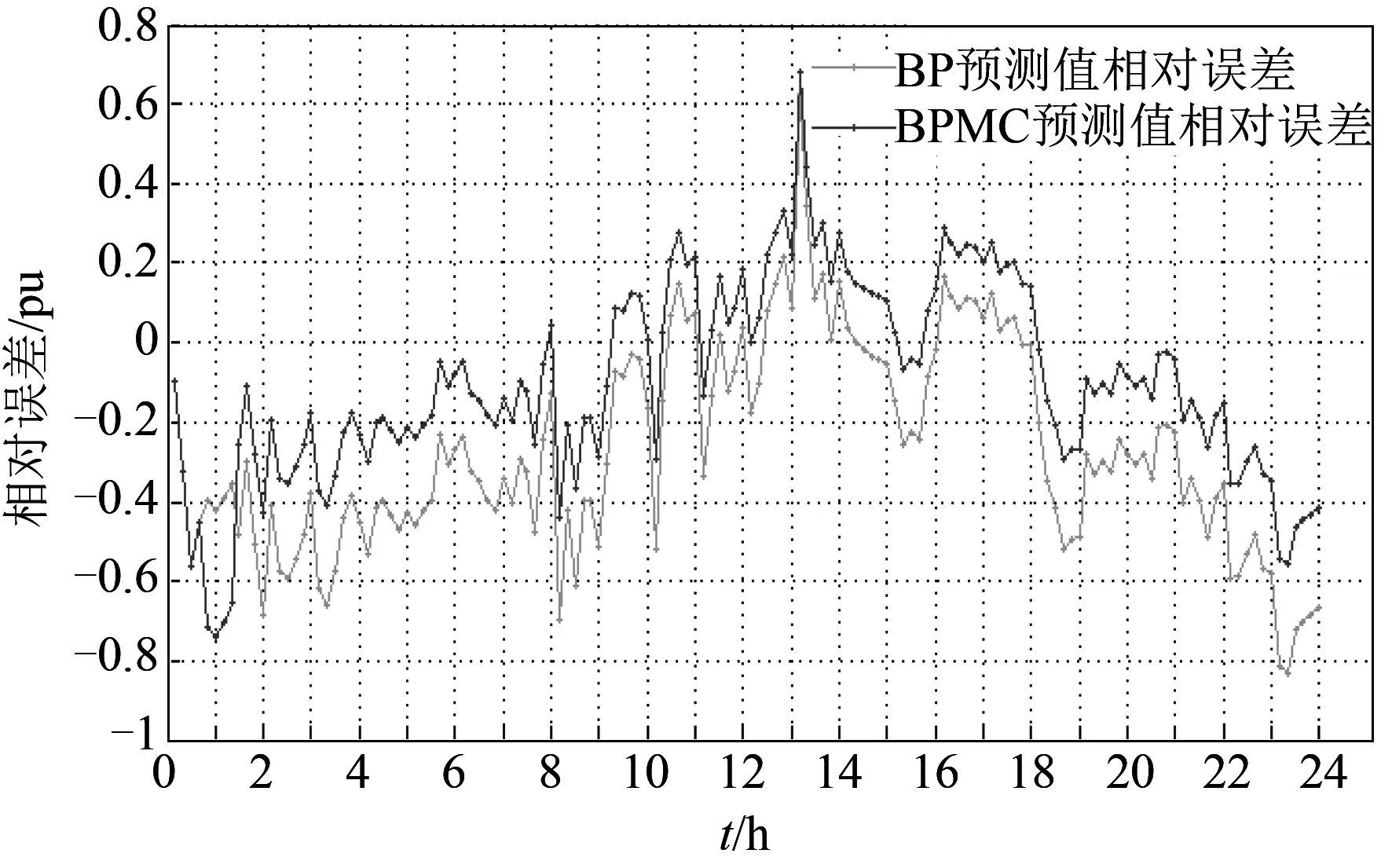
图3 BP与BPMC预测模型的相对误差比较

图4 BP与BPMC预测模型的绝对误差比较

图2显示了传统的BP神经网络法以及改进后的经马尔科夫链残差修正过的BP神经网络模型24 h的预测结果，结果显示，与传统的BP神经网络模型相比，改进后的BPMC模型具有一定的优越性。通过两者的相对误差以及绝对误差的比较，由图3、图4可以看出，BPMC模型较传统的BP模型精确性更高，其中，传统的BP神经网络模型的平均相对误差为27%、平均绝对百分比误差为31.6%，而BPMC模型的平均相对误差为12.53%、平均绝对百分比误差为22.84%，改进后的BPMC模型在一定程度上正向修正了传统的BP神经网络模型的预测值，使其更加逼近真实值。马尔科夫链残差修正模型其本质上是不改变基本预测方法，而增加误差预测模型的一种基于风电功率预测方法使用策略方向的改进方法。该改进方法通过马尔科夫链模型状态转移矩阵对相对误差进行有效预测来弥补BP神经网络模型在风电功率预测结果泛化能力有限的缺陷。

4 结语

本文利用MC适用于波动较大的动态随机过程的特点，首次将MC对BP神经网络法进行残差修正这一模型引入风电功率预测领域。首先采用BP 神经网络法预测风电功率的发展规律，再用MC进行残差修正，该模型综合了BP神经网络法和MC的优点，并将此模型运用至实际风电场中进行模型验证，相比单一的传统BP神经网络预测法，其结果更接近实测值，这证明了BPMC模型的可行性。但是，由于输入数据单一，导致BP神经网络预测的精度较差，从而对整体模型的精度有所影响，这有待进一步的改善。

[1] 范高峰,王伟胜,刘纯,等．基于人工神经网络的风电功率预测[J]．中国电机工程学报,2008,28(34)：118-123.

FAN Gaofeng, WANG Weisheng, LIU Chun, et al. Wind power prediction based on artificial neural artwork [J]. Proceedings of the CSEE，2008，28( 34)：118-123．

[2]崔锦龙,邓姝杰. 基于马尔可夫模型的降水预测及其利用[J]. 资源开发与市场, 2008, 24(2): 115-117.

CUI Jinlong, DENG Shujie. Based on Markov to prediction of precipitation and utilization[J]．Resource Development & Market．2008，24(2)：115-117．

[3]景亚平，张鑫，罗艳.基于灰色神经网络与马尔科夫链的城市需水量组合预测[J].西北农林科技大学学报(自然科学版)，2011,39(7)：229-234.

JING Yaping, ZHANG Xin, LUO Yan. Forecasting of urban water demand based on combining Grey and BP neural network with Markov chain model[J]. Journal of Northwest Sci-Tech Univ of Agr and,2011,39(7):229-234.

Short-TermWindPowerForecastBasedonBPNeuralNetworkResidualErrorModificationModelandMarkovChain

CHEN Juan, CAO Qinyu

(Qingpu Power Supply Company, SMEPC, Shanghai 201799, China)

Wind power forecast is important for large-scale grid-connected wind power operation. This paper makes short-term wind power forecast based on BP neural network residual error modification model and Markov Chain. Through the study of the training samples, use BP neural network for wind power preliminary prediction, obtain the relative error between measured value and predicted value; then modify the relative error by using Markov Chain, which effectively improves the accuracy of the forecast results. The application results show the feasibility of this model and provide a new way for wind power forecasting.

wind power; BP neural network; Markov Chain; short-term forecasting

10.11973/dlyny201705017

陈 娟(1991—)，女，硕士，助理工程师，从事电力营销工作。

TM615.2

A

2095-1256(2017)05-0567-04

2017-07-10

(本文编辑：杨林青)