改进猴群算法优化水声通信盲均衡算法

2017-12-13郭业才

宿州学院学报 2017年11期

高敏,郭业才

1.中国矿业大学物联网(感知矿山)研究中心，徐州,221008；2.淮南职业技术学院信息与电气工程系，淮南,232001;3.南京信息工程大学江苏省气象探测与信息处理重点实验室，南京,2100442

改进猴群算法优化水声通信盲均衡算法

高敏1，2,郭业才3*

针对加权多模盲均衡算法(WMMA)在均衡高阶非常模信号时会出现收敛速度慢、收敛后稳态误差大等问题，提出了一种改进猴群算法优化加权多模盲均衡算法(IMA-WMMA)。新算法中把局部搜索能力较强的单纯形法嵌入基本猴群算法，选用佳点集构造更具遍历性的初始猴群，并给出了自适应爬步长的公式，形成了具有快速全局寻优能力的改进猴群算法(IMA)，将IMA用于初始化盲均衡器的权向量，能有效提高收敛速度，降低稳态误差。水声通信仿真结果表明，与现有的加权多模盲均衡算法(WMMA)和基于遗传算法优化的加权多模盲均衡算法(GA-WMMA)相比，本文算法收敛速度最快，稳态误差最小，星座图最清晰。

盲均衡；猴群算法；佳点集；单纯形法；最优权向量

*通信作者：郭业才(1962-)，安徽安庆人,博士，教授，博导，研究方向：自适应均衡技术与通信信号处理。

1 相关研究与问题提出

水声通信是目前水下远距离无线通信的主要方式。水声信道是一个存在时变、空变、频变且高噪声、强多途、带宽严重受限的极为复杂的无线通信信道[1]，码间干扰十分严重，在接收端引入盲均衡技术是一个很好的解决方法[2]。最为经典的常模算法(Constant Modulus Algorithm,CMA)计算简单，稳健性好，但收敛速度慢，稳态误差大，在均衡高阶QAM(quadrature amplitude modulation)信号时，还存在相位旋转问题[3]。为改善均衡效果，很多学者对CMA进行了一些改进，比如文献[4]将QR分解用于CMA，文献[5]构造了一种可以自适应切换的盲均衡结构，文献[6]在问题优化时采用了共轭梯度法，文献[7]提供了一种基于复指数函数映射的盲均衡算法，文献[8]提出了加权多模盲均衡算法(Weighted Multi-modulus Blind Equalization Algorithm，WMMA)，将信号分为实部和虚部分别进行均衡，同时利用信号幅度和相位信息，有效克服了相位旋转问题，引入的加权项还能使算法的误差模型与QAM方形星座图匹配更精确。但以上种种改进只能在一定程度上优化均衡器的性能，仍存在收敛速度慢、稳态误差大的问题。究其原因，主要是以上算法都归属Bussgang类盲均衡算法，而这类基于随机梯度思想的盲均衡，由于代价函数是高维非凸性的，对均衡器初始权向量非常敏感[9]。当代价函数取得最小值时，盲均衡系统呈现理想状态，若将此时的均衡器权向量系数作为初始值，则能加快收敛速度，减小稳态误差。而原算法中采用随机梯度下降思想的最小化代价函数容易陷入局部最优，若将代价函数取得局部最小值时对应的权向量系数作为均衡器的初始权向量，自然是不理想的，会造成收敛速度慢、稳态误差大等问题。这样看来，Bussgang类盲均衡可以等效为代价函数最小化问题[10]。

为弥补传统方法的不足，智能优化算法被逐渐引入盲均衡算法的优化问题中，例如遗传算法[11]和鱼群算法[12]等，取得了较好的效果，但这些启发式算法都有一个共同的缺点，容易陷入“维灾难”，而盲均衡的代价函数通常是高维的。2008年提出的猴群算法[13](Monkey Algorithm，MA)，算法简单，参数少，并能有效避免“维灾难”，可有效解决30和1 000甚至10 000维度的全局优化问题，性能卓越，自提出以来，已被成功用于求解各类优化问题[14-15]，但同时也暴露出基本猴群算法存在的计算精度不高、局部搜索能力不强等问题。

针对这一问题，本文提出一种改进猴群算法优化加权多模盲均衡算法(Weighted Multi-modulus Blind Equalization Algorithm Based on Improved Monkey Algorithm,IMA-WMMA)，新算法首先对MA作了一些改进，借助佳点集理论构造初始猴群以提高种群的遍历性，给出了自适应爬步长的公式以在保证全局寻优能力的同时提高搜索效率，并在望-跳过程结束后嵌入单纯形法加强局部搜索以提高解的精度，将改进后的猴群算法用于最小化WMMA的代价函数，获取均衡器初始权向量，可逃离局部最优，加快收敛速度，降低剩余误差，改善均衡效果，提高通信质量。在MATLAB中对新算法进行了仿真实验，并将其与文献[8]和[11]中算法进行了对比，实验结果表明，新算法效果更好。

2 改进猴群算法(IMA)

2.1 基本猴群算法(MA)

MA是对自然界中猴群登山爬高过程的模拟，将爬山过程中的爬、望、跳等动作设计成相应的三个搜索过程——爬过程、望-跳过程以及翻过程，通过不断的迭代，最终发现搜索区域内的最高山头，即获取目标函数最大值。MA主要步骤如下：

2.1.1 初始化

MA采用随机的方式在n维搜索空间中生成m只猴子。

xij=xmin,j+(xmax,j-xmin,j)rand

(1)

式(1)中，i=1,2,…,m；j=1,2,…,n；xij为第i只猴子在第j维的实际位置；xmin,j和xmax,j分别表示搜索空间第j维的下界和上界；rand产生一个在区间[0,1]上的实数。

2.1.1 确定适应度函数

若是求取最大值的优化问题，则适应度函数即为待优化的目标函数；若是求取最小值的优化问题，只需作简单的数学处理即可。例如本文是求取WMMA代价函数Q(X)的最小值，故可将Q(X)的倒数作为适应度函数f(X)。

2.1.3 爬过程

在第i只人工猴的当前位置进行随机扰动，在搜索空间生成向量ΔXi=(Δxi1,Δxi2,…,Δxin)，分量Δxij以相同的概率0.5取爬步长λ或-λ(λgt;0)。计算适应度函数在xi处的伪梯度f＇i(xi)=(f＇i1(xi),f＇i2(xi),…,f＇in(xi))，其中

(2)

设向量Y=(y1,y2,…,yn)，向量中各分量为

yj=xij+λ·sign(f＇ij(xi))

(3)

若Y在搜索空间内，则更新位置，Xi←Y；否则，保持位置不变。重复爬过程直至达到预设的爬次数，转入望-跳过程。

2.1.4 望-跳过程

经过不断地攀爬，每只人工猴都到达了各自的山头，此时停下来以视距γ向四周多次眺望，搜索视野范围(xij-γ,xij+γ)内是否有更高的山头，如果有,则立即跳过去。每次眺望的结果用Y=(y1,y2,…,yn)表示，若Y在搜索域内并有f(Y)gt;f(Xi)，则Xi←Y；否则，再次眺望，直到找到满足条件的Y并更新位置，这里的Y必须满足f(Y)≥f(Xi)。转入爬过程，直至达到预设条件转入翻过程。

2.1.5 翻过程

为避免陷入局部最优，有必要给猴群开辟新的搜索领域，翻过程就是为这一目的设计的。在翻过程中，所有猴子向猴群重心方向进行翻跳。在翻区间[c,d]内随机产生一个实数θ，设Y=(y1,y2,…yn)，令

yj=xij+θ(pj-xij)

(4)

2.1.6 解的输出

在整个寻优过程中，猴群遍历的位置对应的适应度函数值最大的即为目标函数的最大值，该位置即为全局最优位置。输出最优解，算法结束。

爬过程作为猴群算法的主要过程，其设计借助了同步扰动随机逼近算法(Simultaneous Perturbation Stochastic Approximation,SPSA)思想，利用了伪梯度信息，与适应度函数的维度无关，故可有效避免“维灾难”，这是基本猴群算法最为显著的一个优点，但运行过程中还存在一些不足,需要加以改进。爬过程中固定步长的设置很难准确把握，步长小，则搜索速度慢；步长大，有可能错过最优解，并且猴群在现实的爬山过程中，也不是固定步长。针对这种情况，本文给出了自适应步长公式。启发式算法对初始种群的优劣比较敏感，猴群算法也不例外，应用佳点集方法构造的初始种群比随机生成的种群分布更加均匀，偏差更小，能更好地保证算法的遍历性，大幅提升算法性能[16]，故本文采用佳点集来构造初始猴群。为加强局部搜索还在望-跳过程结束后引入单纯形法搜索，利用单纯形法的反射、扩张、压缩操作在猴群当前位置加深局部搜索，这样不仅能提高解的精度，还能加快搜索速度。

2.2 佳点集

2.3 自适应步长

本文给出自适应爬步长公式，取代固定爬步长公式，更加符合实际情况。搜索初期，步长较大，保证算法的全局搜索能力；而到搜索后期，更需要强调的是局部搜索精度，这时步长随迭代次数的增加而逐步变小。爬步长的更新公式为

(5)

式(5)中，λmin、λmax分别为爬步长的最小值和最大值，xmin和xmax为搜索空间的上界和下界，t=1,2,…，tmax，tmax为爬过程的最大迭代次数，则公式(3)变为

yj=xij+λ(t)·sign(f＇ij(xi))

(6)

2.4 单纯形法搜索算法

单纯形法具有极强的局部搜索能力[17]，具体步骤如下。

(1)在猴群进入翻过程前，将每只人工猴的位置看成一个搜索点，将所有搜索点带入适应度函数f(X)进行计算并排序，适应度值越大视为越优，适应度值最大的为最优点Xg,适应度值次之的为次优点Xb。计算中心位置Xc：

(7)

(2)随机找出一个较差的点Xs，按公式(8)对其进行反射操作，得到反射点Xr：

Xr=Xc+δ(Xc-Xs)

(8)

式中，δ为反射系数(一般取1)。若f(Xr)gt;f(Xg)，则反射方向正确，按公式(9)执行扩张操作得到扩张点Xe；反之，说明反射方向更差，按公式(10)进行压缩操作得到压缩点Xt。

(3)扩张操作。

Xe=Xc+φ(Xr-Xc)

(9)

式中，φ为扩张系数(一般取2)。若f(Xe)gt;f(Xg)，则用Xe更新Xs；否则，用Xr更新Xs。

(4)压缩操作。

Xt=Xc+ψ(Xs-Xc)

(10)

式中，ψ为压缩系数(一般取0.5)，也是收缩系数。若f(Xt)gt;f(Xs)，则用Xt更新Xs；若f(Xs)lt;f(Xr)lt;f(Xg)，按式(11)进行收缩操作，得到收缩点Xw。

(5)收缩操作。

Xw=Xc-ψ(Xs-Xc)

(11)

如果f(Xw)gt;f(Xs)，则用Xw更新Xs；否则，用Xr更新Xs。

2.5 改进猴群算法

针对基本猴群算法遍历性不足，搜索效率不高，局部搜索能力不强，解的精度较低等种种问题，本文提出了以上改进措施，改进后的猴群算法流程如图1所示。

图1 IMA流程图

步骤1设置算法相关参数，在搜索空间中用佳点集方式构造初始猴群。

步骤2确定适应度函数。

步骤3爬过程中，猴群采用自适应步长进行攀爬，重复设定的爬次数后转入步骤4。

步骤4在望-跳过程中，猴群通过眺望搜寻适宜的位置，完成位置更新后，转入步骤3，直至达到预设望次数后转入步骤5。

步骤5猴群中适应度值较差的M个猴子在单纯形法指导下对当前位置进行局部深度搜索，完成后转入步骤6。

步骤6翻过程为猴群开辟了新的搜索区域，猴群转入步骤3，直至达到预设翻次数后转入步骤7。

步骤7在猴群遍历的所有位置中，对应的适应度值最大的为全局最优值，该位置即为全局最优位置。

3 改进猴群算法优化加权多模盲均衡算法(IMA-WMMA)

IMA-WMMA原理框图如图2所示。

图2 IMA-WMMA原理框图

图2中，a(k)是发射的信源复信号；h(k)是信号传输信道的脉冲响应向量；n(k)是加性高斯白噪声；y(k)是均衡器输入信号；f(k)为均衡器的权系数向量；z(k)为均衡器的输出复信号；s(k)为判决输出的复信号；g(·)为无记忆非线性函数，需满足s(k)=g[z(k)]=z(k)；下标Re和Im分别代表参数的实部和虚部。

3.1 加权多模盲均衡算法

WMMA的代价函数可表示为：

(12)

(13a)

(13b)

WMMA均衡器权向量迭代公式为:

(14a)

(14b)

均衡器输出为:

(15)

WMMA均衡器误差为:

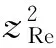
(16a)

(16b)

式(12)～式(16b)构成了WMMA。

3.2 改进猴群算法优化水声信道盲均衡

IMA-WMMA的主要思想是利用IMA较强的全局寻优能力，最小化加权多模盲均衡算法的代价函数，获取均衡器初始权向量，优化均衡效果。主要实施步骤如下：

(1)初始化算法中所有参数。

(2)确定目标函数与IMA适应度函数的关系。本文中IMA适应度函数为 WMMA代价函数的倒数。

(3)均衡器长度即为搜索空间维数，每只人工猴的位置向量对应着一组均衡器权向量。均衡器的输入信号y(k)同时作为IMA的输入信号。通过IMA的迭代寻优捕获WMMA代价函数的最小值，该值对应的人工猴位置向量即为均衡器的理想初始权向量系数。

(4)利用WMMA对信号进行盲均衡并输出。

4 仿真实验

为验证IMA-WMMA的有效性，将WMMA、基于遗传算法的加权多模盲均衡算法(GA-WMMA)、基于猴群算法的加权多模盲均衡算法(MA-WMMA)与IMA-WMMA在水声信道的仿真试验中进行对比。仿真中，发射信号采用16QAM信号和16APSK信号，高斯白噪声的信噪比30 dB，信道为典型的水声信道h=[0.313 2,-0.104 0,0.890 8,0.313 4]，信号采样点均为10 000点，盲均衡器的权长均为16，加权因子λ=1.25，猴群规模为100，爬过程、望跳过程、翻过程的迭代次数分别设置为100、20、5，爬步长最大值和最小值分别为0.001和0.000 1，视野范围取0.005，眺望次数取20。步长参数如表1所示。

16QAM信号500次蒙特卡诺仿真结果如图3所示，16APSK信号500次蒙特卡诺仿真结果如图4所示。

表1 参数设置

图3 16QAM仿真结果

从图3不难看出，在对16QAM信号的均衡中，IMA-WMMA比WMMA收敛快了1 000步，跟MA-WMMA、GA-WMMA收敛速度几乎一致；稳态误差上，IMA-WMMA比WMMA低了近8 dB，比GA-WMMA低了近6 dB，比MA-WMMA低了近2 dB；IMA-WMMA星座图最为清晰紧凑。

图4表明，在对16-APSK信号的均衡中，IMA-WMMA比WMMA收敛快了1 000步，跟MA-WMMA、GA-WMMA收敛速度几乎一致；稳态误差上，IMA-WMMA比WMMA低了近10 dB，比GA-WMMA低了近8 dB，比MA-WMMA低了近6 dB； IMA-WMMA星座图最为清晰紧凑。

均方误差、收敛速度以及星座图的清晰程度是衡量盲均衡算法的重要指标。从以上两个实验明显可以看出，在水声信道中用IMA算法取得的权向量作为WMMA算法的初始权向量，无论对16QAM信号还是16APSK信号，都能有效提高收敛速度，减小均方误差，输出的星座图也更加清晰，均衡质量得以提高。

5 结论

本文提出了改进猴群算法优化加权多模盲均衡算法,借助佳点集理论构造分布均匀的初始猴群，更好地保证了算法的遍历性，给出了自适应步长公式，采用自适应步长提升了算法的搜索效率，在翻过程前引入单纯形法进行局部深度搜索，提高了算法的局部搜索能力，保证了解的精度，将具有快速全局寻优能力的改进猴群算法用于最小化WMMA的代价函数，能获取理想的盲均衡器初始权向量，克服了WMMA算法采用随机梯度思想最小化代价函数易陷入局部最优的问题。水声信道仿真实验证明，本文提出的算法能得到更快的收敛速度，更小的稳态误差，对提升水声通信质量具有一定的意义，但如何将算法移植到硬件系统中还需要作进一步的研究。

图4 16APSK仿真结果

[1]贾宁,黄建纯.水声通信技术综述[J].物理,2014,43(10):650-657

[2]童峰,许肖梅,方世良,等.改进支持向量机和常数模算法水声信道盲均衡[J].声学学报,2012,37(2):143-15

[3]马思扬,彭华,王彬.适用于稀疏多径信道的稀疏自适应常模盲均衡算法[J].通信学报,2017,38(1):150-157

[4]Ragheb A M,Shoaib M,Alshebeilis S,et al.Enhanced blind equalization for optical DP-QAM in finite precision hardware[J].IEEE Photonics Technology Letters,2015,27(2):181-184

[5]曾乐雅,许华,王天睿.自适应切换双盲盲均衡算法[J].电子与信息学报,2016,38(11):2780-2786

[6]李进,冯大政,刘文娟.快速QAM信号多模盲均衡算法[J].电子与信息学报,2013,35(2):273-278

[7]饶伟,高惠娟,段美怡,等.一种新的基于复指数函数映射的盲均衡算法[J].电子学报,2016,44(5):1009-1016

[8]许小东,戴旭初，徐佩霞.适合高阶QAM信号的加权多模盲均衡算法[J].电子与信息学报,2007,29(6):1352-1355

[9]王大磊.基于优化理论的盲均衡技术研究[D].郑州:解放军信息工程大学信息系统工程学院,2014：8-10

[10]王尔馥,郑远硕,陈新武.部分精英策略并行遗传优化的神经网络盲均衡[J].通信学报,2016,37(7):193-198

[11]Zhu Ting-ting,Zhao Li,Zhang Feng.Dual-mode genetic blind equalization algorithm based on error signals[J].Technical Acoustics,2016,35(8): 385-388

[12]郭业才,王慧，吴华鹏.新变异DNA遗传人工鱼群优化DNA序列的多模算法[J].科学技术与工程,2016,16(3):66-71

[13]Zhao Ruiqing,Tang Wansheng.Monkey algorithm for global numerical optimization[J].Journal of Uncertain Systems,2008,20(3):164-175

[14]张佳佳,张亚平,孙济州.基于猴群算法的入侵检测技术[J].计算机工程,2011,37(14):131-133

[15]贾赛赛，刘志勤，杨雷，等.基于混合猴群算法的凸多面体碰撞检测[J].计算机工程与设计,2016,37(10): 2789-2793

[16]钟明辉,龙文.一种随机调整控制参数的鲸鱼优化算法[J].科学技术与工程,2017,17(12):68-73