基于滑模观测器的磁通切换型记忆电机永磁磁链辨识研究

(无锡职业技术学院，江苏无锡， 214121)

基于滑模观测器的磁通切换型记忆电机永磁磁链辨识研究

壮而行

(无锡职业技术学院，江苏无锡， 214121)

近年来一类采用高剩磁、低矫顽力永磁材料的记忆电机得到了广泛的研究。这类电机可以通过施加电流脉冲直接调节永磁体的磁化水平，从而大大拓宽电机的弱磁调速范围。记忆电机在运行过程中的永磁磁链是可变的，仅依靠离线实验所得的反电动势/电流表格无法精确得出电机的磁链，因此需要在线观测永磁磁链幅值。为此设计了基于q轴电压方程的永磁磁链滑模观测器，分析了观测器稳定性和参数选择依据，仿真计算证明了提出的永磁磁链观测器的有效性。

磁通切换；记忆电机；永磁磁链辨识；滑模观测器；仿真研究

0 引言

现代高性能永磁同步电机(Permanent Magnet Synchronous Machine, PMSM)一般采用钕铁硼(NdFeB)永磁，具有高效率、高功率密度、结构简单、控制方便等优点[1，2]。但是这种永磁电机的调速范围受到电机磁链、电感等固有特性的限制；而且在发电运行时，故障灭磁困难，限制了其应用范围。为了增强永磁电机的气隙磁场调节能力，近几年来，一类能够通过直接改变永磁体磁化水平调节气隙磁场的电机-记忆电机(Memory Machine， MM)，受到了国内外部分研究者的重视并取得了突破性进展。这类永磁电机采用高剩磁、低矫顽力的永磁材料，如铝镍钴(AlNiCo)，可通过施加瞬时脉冲改变永磁体的磁化水平，实现气隙磁场的调节，几无电励磁损耗，可以简单高效地实现在线调磁。

记忆电机的永磁磁链根据运行需要是可变的，仅通过调磁电流-磁链关系表格无法保证调磁的正确性，因此需要加入永磁磁链辨识算法，与空载试验中所得数据互相验证。

最传统的测量电机磁链的方法是在电机中埋入探测线圈，通过测量感应电动势的方法测量电机磁链，但是这种方法需要改变电机的结构，可能影响电机的性能。近年来，国内外学者利用控制电机所必需测量的电流、转速、电压信号，采用现代控制理论和信号处理技术，观测电机的永磁磁链等参数。文献[3]利用模型参考自适应(Model Reference Adaptive System，MRSA)的方法，在使用id=0控制的情况下利用q轴电压方程对电机参数进行了辨识。文献采用两步法，首先将电压方程中的电阻值设定为设计值，再辨识转子磁链。文献[4]在采用模型参考自适应算法的基础上，利用Popov超稳定理论设计自适应律，采用分步辨识的方法对表贴式永磁同步电机进行多参数辨识，仿真和实验证明了该方法的有效性。文献[5]利用扩展卡尔曼滤波(Extended Kalman Filter，EKF)的方法对电机的永磁磁链进行了观测，在观测时考虑了编码器位置反馈误差的影响，实验表明该方法可以不受位置误差的影响快速观测永磁磁链。文献[6]提出了一种自适应线性元件神经网络法识别电机参数。该方法电机在静止状态时，通过注入d轴电流测得定子电阻，在电机起动过程中，将电阻设为静止情况下的估计值，然后辨识出电机转子磁链。该方法计算量小，每步迭代只需少量的加减运算，适于编程实验。实验验证了该方法的可行性。文献[7]采用量子遗传算法对永磁电机的参数进行辨识，在辨识过程中对逆变器非线性导致的电压畸变进行了补偿，提高了辨识算法的精度。

某课题组提出将磁通切换原理与记忆电机的概念相结合，在文献[8～9]中提出了多种不同结构的磁通切换型永磁记忆电机(Flux Switching Memory Machine, FSMM)，该类电机的铝镍钴永磁体、电枢绕组和调磁绕组均位于定子上便于散热，直流调磁绕组和电枢绕组在电气上隔离，便于进行解耦控制。本文将以这类电机为对象，研究其调磁控制策略。

1 记忆电机的结构和数学模型

1.1 电机的结构

图1所示为一种12/14极的磁通切换型内嵌式永磁记忆电机。其中，三相集中电枢绕组均匝绕在定子齿上，铝镍钴永磁体内嵌于定子，并匝绕以直流脉冲调磁绕组。电机的磁通切换原理所示。当转子从位置A运行到位置B时，电枢绕组匝链的磁链极性发生了交变，在运行原理上继承了磁通切换原理，因此永磁磁链和相反电动势波形也有较好的正弦性，十分适合无刷交流运行。同时，从电机运行结构可以得出，当在调磁绕组中施加瞬时正或负直流脉冲电流时，各块永磁体将在一个电周期内被充磁或去磁到相同的磁化水平，电机有较高的调磁效率。

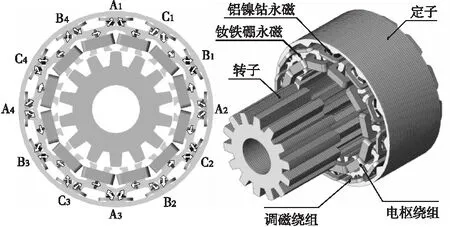
图1磁通切换型内置式记忆电机的结构

图2内嵌式结构磁通切换原理(充磁)

1.2 磁通切换型记忆电机的数学模型

为了对记忆电机进行控制，首先需建立记忆电机的数学模型。其建模方法可以比照普通磁通切换型电机[10]和混合励磁电机[11]进行。

在两相旋转dq坐标系下，其磁链方程为

(1)

式中，id、iq—d、q轴电流；Ld、Lq、Lf—d、q轴和调磁绕组电感；Msf—调磁绕组和d轴的互感；ψpm—直轴电枢绕组所匝链的永磁磁链幅值；ψfpm—穿过调磁绕组的永磁磁链。在不施加调磁电流的情况下，ψpm、ψfpm—恒定不变的直流量；在调磁动态中，这两个磁链值均为调磁电流的函数。

电机的电压方程为

(2)

式中，ud、uq—dq轴下的等效电枢电压；id、iq—dq轴下的等效电枢电流；uf—调磁绕组电压；if—调磁绕组电流；Rs、Rf—定子和调磁绕组的电阻；ωe—电机的电角频率。

由于调磁过程的存在，电机的动态转矩方程比较复杂。如果调磁电流近似为梯形波，且电机dq轴电流响应较快，能很快稳定，永磁磁链也进入稳态，那么在调磁电流平直时，电机的电磁转矩为电机的转矩方程为

Te=1.5piq[ψpm+(Ld-Lq)id+Msfif]

(3)

式中，p—电机的极对数，对于FSMM即为转子极数。

2 滑模永磁磁链观测器

文中提出的永磁磁链辨识算法各具优势，但也存在各自的不足之处，如扩展卡尔曼滤波法涉及矩阵运算，运算量较大；非线性自适应元件法需要选择适当的收敛因子，否则可能会出现观测器不收敛的情况。本章借鉴无位置控制中常用的滑模观测器法[12]，建立基于q轴电压方程的永磁磁链滑模观测器，对不同磁化状态下的永磁磁链进行辨识。

2.1 滑模观测器原理

滑模变结构控制由前苏联学者Emelyanov在上世纪50年代首先提出，是一种控制表现为不连续性的非线性控制。该控制策略根据系统在动态过程中的当前状态切换不同的系统结构，控制系统按照预定的滑动模态状态轨迹运动。经过国内外学者的不断研究与完善，该理论已经成为自动控制领域中的经典控制方法。

2.2 滑模变结构控制的数学描述[13]

假设有下列非线性系统

(4)

式中，x∈Rn，u∈Rn—系统的状态向量和控制向量，控制量u=u(t,x)按以下逻辑在切换面S(t,x)=0上切换

(5)

式中，ui(t,x)、Si(t,x)—u(t,x)、S(t,x)的第i个分量；ui+(t,x)、ui-(t,x)、Si(t,x)—适当的光滑连续函数。

为使滑模变结构控制能成立，必须满足以下滑动模态存在的充分条件。

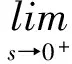
(6)

(7)

或

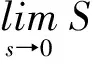
(8)

式(6)～式(8)既是保证滑动模态存在的充分条件，也是保证切换面外的相轨迹在有限时间内到达切换面的条件。

同等意义下的滑动条件如图 3所示，其表达式为

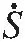
(9)

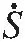
(10)

图3滑动模态到达条件

2.3dq坐标系下磁链观测器的设计

滑模观测器常用于永磁同步电机无传感器控制中，观测器建立于两相静止αβ坐标系下，通过观测永磁磁链获得转子位置。由于本文控制的电机有转子位置信号反馈，因此将观测器建立在dq坐标系下，这样永磁磁链仅存在于q轴方程中，且为直流量，便于滤波器的设计，可以减少抖振和观测误差。

忽略永磁电机的饱和与损耗时，电机在dq轴系坐标下的状态方程为

(11)

由于永磁磁链只在q轴方程出现，因此将q轴方程写为以下形式

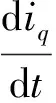
(12)

式中，A=-R/Lq,B=1/Lq,u=uq-Ldωeid，Ke=-1/Lq，eq—永磁磁链在q轴的旋转电动势。

基于式(12)，构造如下的滑模观测器方程

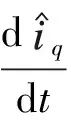
(13)

式中，符号“^”代表估计值，K—观测器开关增益。

(14)

用式(13)减去式(12)，如果式中电机参数一致，则有

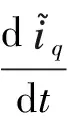
(15)

(16)

将式(15)代入式(16)得

(17)

Kgt;eq

(18)

满足这一条件，就能产生滑模运动，误差动态式(15)就是渐进稳定的，也保证了观测方程的收敛。

由式(18)可知，观测方程的收敛需要开关增益足够大，但是过大的开关增益会造成不必要的抖振噪声，造成估计误差。为了充分抑制抖振，可以采用如下自适应律

(19)

式中，λ—适当选择的大于1的常数。

当状态点达到超平面以后，有

(20)

将式(20)代入式(15)，可以得到等效的连续输入信号为

(21)

2.4 观测器离散化

为了能让观测器能在数字系统中实现，需要对观测器的数学模型进行离散化。设状态空间方式形式如下

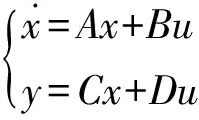
(22)

若系统的采样周期为T，则离散时间状态空间表达式为

(23)

式中

(24)

当采样周期T较小时，离散化的状态方程可以近似表示为

x(k+1)=TAx(k)+TBu(k)

(25)

将式(13)写成如下形式

(26)

对照式(23)～式(24)，其离散时间状态空间表达式为

(27)

其中

(28)

3 仿真分析

根据上节提出的记忆电机磁链辨识策略，表1为电机参数。根据上文提出的永磁磁链滑模观测器的原理，在Matlab/Simulink中搭建仿真模型如图 4所示，其中FSMM模块为记忆电机本体模块，电机参数如所示通过Flux模块的变化仿真电机在调磁状态下永磁磁链的变化。

表1 电机参数

永磁磁链观测器仿真模型如图4所示。模型的输入量为dq轴电流，d轴电压以及电机电角速度，输出量为永磁磁链在q轴的旋转电动势。输出量经一阶低通滤波器滤波后，除以电机电角速度，即可得观测到的永磁磁链幅值。永磁磁链滑模观测器模型见图5。

图4仿真模型

图5永磁磁链滑模观测器模型

对上述模型进行仿真，仿真场景如下：电机空载启动，给定转速700r/min，在0.3s时突加3 N·m转矩；在0.5～0.6s施加调-5.5A的去磁脉冲电流，电机永磁磁链从0.08Wb降至0.04Wb；在0.7～0.8s施加15A的增磁脉冲电流，电机永磁磁链从0.04Wb增至0.08Wb，仿真所得电机磁链波形和观测到的磁链波形见图6，图中点线为q轴旋转电动势对应的磁链实际值，实线为磁链观测值。

从图5中可以看出，在电机启动阶段磁链观测值可以很快稳定到实际值；在0.3s突加负载时，观测值受到扰动后很快恢复稳定；在0.5～0.6s和0.7～0.8s时，电机处于调磁阶段，所观测磁链为永磁磁链和调磁绕组产生磁链的叠加，在调磁动态中，观测值也能很快跟踪实际值。永磁磁链仿真波形见图6。图6(b)为观测值的放大波形，波形显示经滤波后，观测值的抖振很小，具有较高的观测精度。

图6永磁磁链仿真波形

4 结语

本文为了保证记忆电机调磁的准确性，本章提出了一种磁链滑模观测器以观测永磁磁链的大小；介绍了滑模观测器的原理，基于电机q轴电压方程建立了观测器方程，分析了观测器稳定性及相应的开关增益选择原则；为方便数字实现，对观测器进行了离散化。利用Matlab/Simulink仿真软件搭建了观测器的仿真模型，进行了永磁磁链观测的仿真研究；仿真结果证明了所提出观测器的可行性。

[1] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2001, 24-32.

[2] 王秀和. 永磁电机[M]. 北京: 中国电力出版社, 2011, 21-28.

[3] Rashed M, MacConnell P F, Stronach A F,et al. Sensorless indirect-rotor-field-orientation speed control of a permanent-magnet synchronous motor with stator-resistance estimation. Industrial Electronics, IEEE Transactions on, 2007, 54(3):1664-1675.

[4] 杨宗军, 王莉娜. 表贴式永磁同步电机的多参数在线辨识[J]. 电工技术学报,2014,(03): 111-118.

[5] 肖曦, 张猛, 李永东. 永磁同步电机永磁体状况在线监测[J]. 中国电机工程学报,2007,(24): 43-47.

[6] 刘侃, 章兢. 基于自适应线性元件神经网络的表面式永磁同步电机参数在线辨识[J]. 中国电机工程学报,2010,(30): 68-73.

[7] Liu K, Zhu Z Q. Quantum Genetic Algorithm Based Parameter Estimation of PMSM under Variable Speed Control Accounting for System Identifiability and VSI Nonlinearity. IEEE Transactions on Industrial Electronics, 2014:1.

[8] Yang H, Lin H, Dong J,et al. Analysis of a Novel Switched-Flux Memory Motor Employing a Time-Divisional Magnetization Strategy. IEEE Transactions on Magnetics, 2014, 50(2):849-852.

[9] Hui Y, Heyun L, Zhu Z Q,et al. Novel switched-flux hybrid permanent magnet memory machines for EV/HEV applications[C]. Electrical Machines and Systems (ICEMS), 2014 17th International Conference on, 2014:1191-1195.

[10] 贾红云, 程明, 花为, 等. 磁通切换永磁电机等效模型与控制策略分析[J]. 电机与控制学报,2009,(05): 631-637.

[11] 杨成峰. 新型混合励磁同步电机的分析、设计及控制策略研究[D]. 东南大学, 2007.

[12] 王成元, 夏加宽, 孙宜标. 现代电机控制技术[M]. 北京：机械工业出版社, 2009.

[13] 王丰尧. 滑模变结构控制[M]. 北京：机械工业出版社, 1998.

IdentificationResearchonPermanentMagnetFlux-LinkageofFlux-SwitchingMemoryMachineBasedonSlidingModeObserver

ZhuangErxing

(Wuxi Institute of Technology, Wuxi 214121, China)

A kind of memory machines (MMs) equipped with PM material of low coercivity and high remanence were extensively investigated recently. This kind of machines can directly adjust magnetization level of permanent magnet by applying a current pulse, thereby widely expand speed adjustment range of weak magnetic field. Since the PM flux-linkage of memory machine is variable during operation, it is hard to obtain the accurate value by back EMF/current table based on off-line experiment. Therefore, it is quite necessary to online observe the magnitude of PM flux-linkage. Therefore, a sliding mode PM flux-linkage observer based on q-axis voltage equation was designed. The operating stability and parameter selection criterion of the observer were analyzed. The simulation result proves effectiveness of the proposed PM flux-linkage observer.

Flux switching；memory machine；PM flux-linkage identification；sliding mode observer；simulation research

10.3969/J.ISSN.1008-7281.2017.06.05

TM303.3

A

1008-7281(2017)06-0014-006

壮而行男1989年生；毕业于东南大学电气工程学院，研究方向为电机控制.

2017-06-01