基于介质光栅导模共振的多频率点的单向通光

田徐腾越，高华*,许玲玲

（1北京市第八中学，北京100032；2中国地质大学数理学院，北京 100083；3首都师范大学物理系，北京 100048；4北京市铁路第二中学,北京100045）

基于介质光栅导模共振的多频率点的单向通光

田徐腾越1，高华2，3*,许玲玲4

（1北京市第八中学，北京100032；2中国地质大学数理学院，北京 100083；3首都师范大学物理系，北京 100048；4北京市铁路第二中学,北京100045）

单向通光是指只允许光波从一个入射方向上通过，反方向入射时光波全部被截止。单向通光元件即光二极管是实现光计算、光互联等功能中非常重要的一个基本光学元件。本文设计并提出了一种可实现多频率点单向通光的光栅光学单通元件,其原理在于通过波矢匹配条件单方向地激发光栅基底层的波导模式共振，抑制光栅高衍射级的透射，从而获得光学非对称透射，并通过优化光栅结构参数进而获得单向通光的透射效果。时域有限差分方法模拟结果表明：在共振波长处，其正、反向透过率可以分别达到0%到90%，单透效果远远优于非对称金属光栅系统的单透效果。此外，该单透元件还具有结构简单，无吸收，对光波偏振态没有依赖等诸多优点，尤其适用于现代硅基纳米光子线路的集成结构。

单向通光；波导模式共振；通道效应；波矢匹配；介质光栅

单向通光元件也就是我们常说的光二极管，因其在现代光学通信以及未来的光计算方面的潜在应用，得到科研工作者越来越多的关注[1-2]。传统获得单向通光的方法是利用法拉第效应或者非线性效应，用磁光材料或非线性材料打破时间反演对称性从而得到非对称透射[3-4]。但是，这些方法不仅需要强磁场或强光场，而且设备庞大复杂，在现代集成光路中难以适用，尤其是当硅基纳米光子学出现以后，要在芯片上以前所未有的微小尺度建立光学集成系统，研制与之适应的微纳尺度的光二极管单通元件就变得越来越迫切，于是科研工作者把研究热情投向了线性材料、非磁性材料微纳尺度的非对称透射上。

近年来，基于金属微纳结构表面等离子体激元的新型光学二极管结构不断被提出[5-7]。与之前提到的传统非线性或磁性单向通光元件相比，这种结构具有几个突出的优点：一是它尺寸更小，结构更简单，利于集成；二是它不需要非线性材料、磁光材料等特殊材料,常规的金属材料就能够实现；三是它在斜入射和垂直入射条件下都适用。然而，表面等离激元只有在金属和介质的分界面才能够激发。换句话说，由于金属材料的存在，吸收是必然的，这将不可避免地抑制正向透射以及两个相反方向的透过率之差。在已有文献报道的单向通光元件中，基于表面等离激元的最大正反向透射率之差约为60%，许多甚至不高于40%[8-9]，这对于实际应用标准还远远不够。此外，表面等离激元只能由横磁场（TM波）在一定共振频率处激发。也就是说，这种光学二极管只能对TM波在某一单一频率处有效，对别的频率点处则不能实现单向通光，大大限制了它的使用。针对这一情况，本文中设计并提出了一个结构非常简单的基于导模共振的介质光栅单通结构，用更为简单的器件实现了一种更高质量的单向通光效果。这种结构不仅没有吸收，正反向透射率差可以达到90%，而且因为光栅导模共振对TM和TE波（横电场）都可以激发，这种非对称透射也可以用于TE偏振波。除此之外，多个模式的导模共振可以同时被激发，所以这种单向通光元件还可以在多个频率条件下同时工作。本文介绍我们提出的单透元件的结构、效果、机制及与之相关的讨论与分析。

1 单向透射元件的光栅结构与透射光谱

本文提出的单向通光元件的结构如图1所示，它是一层氮化硅（SiNx）介质薄膜，在其上侧刻有周期性的刻槽。光栅槽和光栅脊的宽度分别用a和b表示。槽的深度和基底的厚度由h1和h2表示。图中建立了笛卡尔直角坐标系，TM偏振的线偏振光沿着y方向垂直入射，其电场沿着x方向磁场沿着z方向。为简单起见，沿+y方向和-y方向入射的光分别称为正向入射和反向入射。采用加拿大Lumerical公司的商业计算软件FDTD Solutions模拟光波与该介质光栅的相互作用。在模拟过程中，为了提高计算效率，只取一个光栅周期进行计算，计算区域在y方向和x方向分别用理想匹配层和周期性边界条件来截断。计算时光栅的结构参数取a=b=0.5 μm，h1=0.65 μm，h2=1.4 μm，氮化硅的折射率选为1.75。

图2给出了计算所得透射光谱的结果，其中蓝色实线和红色虚线分别表示反向入射和正向入射时的透射光谱。

图1 SiNx介质光栅和光波入射方向示意图

图2 光栅分别在正向、反向垂直入射时其透射谱图

由图2可以看出：

（1）2条透射曲线显示了完全不同的透射特点。对于反向透射，在共振波长处λ=677.9 nm，729.9 nm，782.8 nm和829.4 nm，呈现了几个非常尖锐的共振谷值，透射率几乎达到0，而其余频率处的透过率则高得多，在90%附近波动。与此相反，正向入射时，透射光谱近似为一个正弦函数，在透过率为80%-100%之间波动。

（2）在反向透射曲线发生共振的频率位置，正向透射谱也表现出微小的共振，但是它对透过率的影响微乎其微，其透过率值依然很高。因此，在这些共振频率点的位置，2个相反方向的光栅透过率截然不同，最大的差别可以达到90%（λ=782.8 nm），获得了非常好的非对称透射效果，比金属光栅结构中基于表面等离激元共振获得的透过率之差要高很多。

（3）用这样一个非常简单的介质光栅结构，可以在多个工作波长处同时获得高质量的单向通光效果，这种介质光栅可以作为一个非常理想（结构简单，无吸收，单透效果好）的单透元件来使用。

2 单向透射的物理机理分析

为了探究该光栅透射谱中出现的多重共振的原因，同时揭示上述单向通光现象的物理机制，我们提取了光波与光栅相互作用时，一个光栅周期内的磁场强度分布，如图3所示。它给出的是在λ=829.4 nm处的磁场，其中图3a和图3b分别对应了反向入射和正向入射情形。本文没有给出其他共振波长处的磁场强度分布，但是它们与图3基本相似，唯一不同的是发生共振的模式数不同。图3中的白线表示氮化硅光栅的边界。

图3显示：反向入射时，在光栅基底的介质层中电磁模式共振被激发，它在x方向（水平方向）上的模式数为m=4。与此相反，正向入射时，磁场分布较为均匀，没有任何电磁场的局域现象，即没有激发任何形式的电磁模式共振。

以往的研究结果表明，在一个光栅结构中可能存在多种类型的电磁共振，它包括金属结构中的表面等离激元共振，光栅狭缝处的腔模共振，光栅基底波导层的导模共振以及复合光栅的相位共振等。通过研究比较各类共振的激发条件、共振特性以及各自发生共振的位置，初步判定这种基底介质层中的共振为波导模式共振。

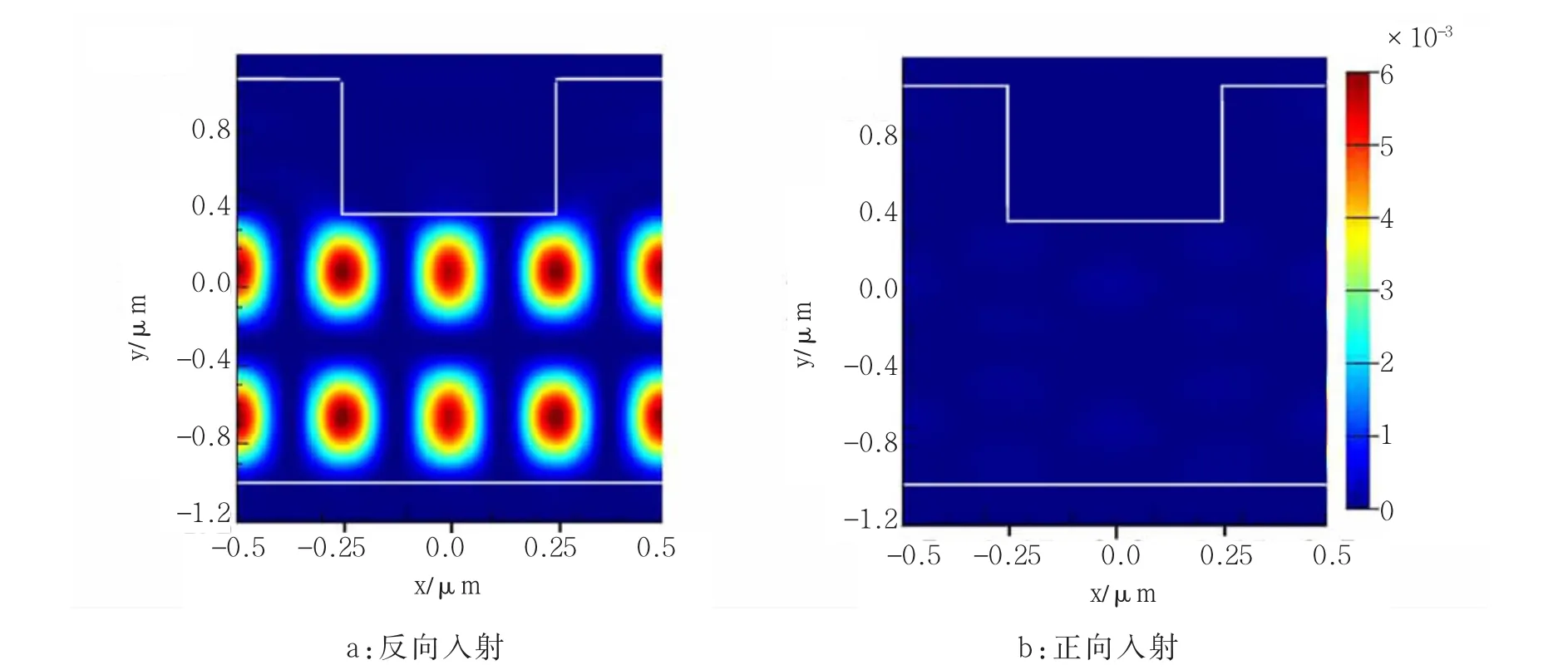
图3 光栅一个周期内的磁场强度分布

为了进一步证实这种共振为波导模式共振，采用对称的三层“空气/氮化硅/空气”平板波导模型结构进行理论解析与验证。众所周知，光栅中导模共振发生时，光波全部被反射，形成尖锐的反射共振峰，这与透射谱中透过率急剧减小相吻合[10]。但是导模共振的发生需要满足波矢匹配条件。在这个结构中，水平方向上的波矢由光栅高级衍射所携带的波矢水平分量来提供。这就要求被激发的导模的传播常数β等于光栅矢量KP=2π/P的整数倍，其中P为光栅的周期。而对于这种三层对称平板导波，已知它的色散关系如下[11]：

式中：m是共振模式数，K0是自由空间中的波数，n1是三层对称结构中外层材料的折射率，此处为空气，所以折射率取为1。此外，波导中心层的厚度和折射率分别为td和nd，这里应取光栅基底的参数：td=1.4 μm，nd=1.75。TM导模由ρ=1表示（TE导模由ρ=0表示）。

图4给出了用式(1)计算的TM波的不同模式数所对应的色散关系曲线。周期为P=a+b=1 μm的介质光栅对应的光栅矢量为KP=0.00628 nm-1。红色水平线示出β=2KP的关系。在所计算的波长范围内，色散关系曲线与水平线 β=2KP在 λ=669.5 nm，723.6 nm，778.8 nm和827.5 nm有交点，如图4中的黑点所示，在这些位置处，波矢匹配条件满足，导模共振可以激发。但是这些点的波长比图2中的谐振波长略小。这是因为该空气/氮化硅/空气平面波导模型与本文提出的光栅结构略有差别，是本文提出的光栅结构在b=0时的理想近似模型。当逐渐减少参数b重复计算时，图2中共振骤降的位置将越来越接近图4中黑点位置，且最终重叠在一起。由此可以得出：在光栅基底中发生的电磁模式共振是波导模式共振。

图4 介质平板波导中TM波不同模式数所对应的色散关系曲线

将整个光栅视为一个两层结构，即一个无支撑的光栅层和一个平板波导层（基底）。如果平面波从光栅一侧入射，则由于光栅的作用首先发生光波衍射。高衍射级将携带一个水平方向的传播波矢，当这个传播常数与基底层导模共振所需的波矢匹配常数相等时，波矢匹配条件得以满足，导模共振被激发，衍射光被反射。反之，如果平面波从光栅基底一侧入射时，它将直接透过光栅基底层（基底为透明介质层）到达光栅层，再经光栅衍射几乎全部透射过去。没有光可以被光栅层反射进入光栅基底层，波矢匹配条件难以实现，所以正向入射时导模共振无法激发。

3 讨论

本文提出的这种单通结构与其他单通结构相比，具有以下明显的优点：

（1）结构非常简单，只需对一层氮化硅介质材料进行简单的周期性刻蚀即可得到，尺寸可以小到微纳米量级，比传统的非线性和磁性材料单通装置要小巧轻便得多，有利于集成。

（2）相对于近年来提出的基于表面等离激元的金属单通元件，这种元件没有吸收，正负透过率之差可高达90%，单通效果得到了明显的提高。

（3）以上的计算与分析针对的均是TM偏振波，而对于TE波，类似的单向通光的效果也可以得到。TM波和TE波之间唯一的不同就是光栅基底层导模共振的激发条件。方程(1)中ρ将取值0而不是1。这导致TE波具有不同的共振频率。然而，根据TM模和TE模的色散关系，通过优化光栅参数，对TM波和TE波可以得到相同的共振频率，即TM波和TE波的单向通光的效果可以同时获得。这也比金属光栅中只对TM波获得的单向通光更具有使用价值。

4 结论

（1）本文提出的光学单通元件实现了多个频率点同时作用的单向光学传输，多频率点的单向通光相对于以往单频率点的单向通光是一大进步，尤其是在波分复用通讯网络更具有优势。

（2）这种单向通光的机理来源于光栅基底层的波导模式共振，共振的发生是由于光栅层的高级衍射光给波导共振提供了波矢匹配条件。

（3）导模共振对于TM波和TE波均能激发，这种单向的通光对于这两个偏振态的光波都可以获得，且可以通过调整光栅结构参数使得TE波、TM波共振同时激发，单透同时获得。

（4）该单通元件结构简单，体积小，单通质量高而且性能稳定，可以作为硅基集成光路中的全光二极管使用，解决了传统单通元件无法集成的困难，尤其是对于近些年硅基微纳集成光学的发展提供了有益的帮助。

[1]Wang C，Zhong X，Li Z Y，et al.Linear and passive silicon optical isolator[J].Sci Rep，2012，2(9):674.

[2]Cicek A，Yucel M B，Kaya O A.Refractionbased photonic crystal diode[J].Opt Lett，2012，37(14):2937-2939.

[3]Haldane F，Raghu S.Possible realization of directional optical waveguides in photonic crystals with broken timereversal symmetry[J].Phys Rev Lett，2008，100(1):145-150.

[4]Lepri S，Casati G.Asymmetric wave propagation in nonlinear systems[J].Phys Rev Lett，2011，106(106):164101-164101.

[5]Xu J，Cheng C，Kang M，et al.Unidirectional optical transmission in dualmetal gratings in the absence of anisotropic and nonlinear materials[J].Opt Lett，2011，36(10):1905-7.

[6]Stolarek M，Yavorskiy D，Kotyński R，et al.Asymmetric transmission of terahertz radiation through a double grating[J].Opt Lett，2013，38(6):839-841.

[7]Gao H，Zheng Z Y，Hao H Y，et al.Mechanism of optical unidirectionaltransmission in subwavelength dual-metal gratings[J].Appl Phys B，2014，114(3):401-406.

[8]Battal E，Yogurt T A，Okyay A K.Ultrahigh contrast oneway optical transmission through a subwavelength slit[J].Plasmonics，2013，8(2):509-513.

[9]Hu X Y，Zhang Y B，Xu X N，et al.Nanoscale surface plasmon all-optical diode based on plasmonic slot waveguides[J].Plasmonics，2011，6:619-624.

[10]麻健勇，刘世杰，魏朝阳，等.反射型导模共振滤波器的设计[J].物理学报，2008，57(2):827-832.Ma J Y，Liu S J，Wei C Y，et al.Design of reflection resonant grating filters[J].Acta Physica Sinica，2008，57(2):827-832.

[11]Park C H，Yoon Y T，Lee S S.Polarization-independent visible wavelength filter incorporating a symmetric metaldielectric resonant structure[J].Opt Express，2012，20(21):23769-23777.

Multi-frequency unidirectional optical transmission based on guided mode resonance in a dielectric grating

Tian Xutengyue1,Gao Hua2，3*,Xu Lingling4
(1 Beijing No.8 High School,Beijing 100032,China;2 China University of Geosciences Beijing,School of Science,Beijing 100083,China;3 Capital Normal University,Department of Physics,Beijing 100048,China;4 Beijing Railway No.2 Middle School,Beijing 100045,China)

Unidirectional optical transmission,also named optical diode,it permits optical wave to transmit from one incident direction while prohibit it completely when the light wave incidents form the reversed direction.It is one of the most important optical elements of the optical calculation and optical connections.In this paper,a grating element which can obtain unidirectional optical transmission at multiple frequencies was proposed.The mechanism is that guided mode resonances in the substrate of dielectric grating can be stimulated in an one-way manner by wave vector matching condition,the high diffraction orders are accordingly depressed and then asymmetric transmission is realized.Through further optimizing the structural parameters ofthe dielectric grating,unidirectionaltransmission was also obtained.The simulated results by using Finite-Difference Time-Domain technique demonstrate that the transmittances in forward and backward directions can reach 90%and 0%,respectively,which is far better than the unidirectional transmission effect obtained in the asymmetric metallic grating system.Furthermore,this kind of unidirectional transmission element is structural simple,non-absorptive,independent of the polarization states of the incident light.Therefore it is specially suitable for the modern on-chip integrated nanometer optical systems based on silicon.

unidirectional optical transmission;guided mode resonance;channel effect；wave vector matching;dielectric grating

O439

A

10.13880/j.cnki.65-1174/n.2017.05.023

1007-7383(2017)05-0657-04

2017-04-18

国家自然科学基金项目（11504336），中央高校基本科研业务费（265201430）

田徐腾越（2000-），男，高中生，擅长物理与数学。

*通信作者：高华（1978-），女，副教授，从事微纳光学研究，e-mail:gaohua@cugb.edu.cn。