简单有效的PID温控算法
2017-12-12胡传志沈建华彭晓晶
胡传志,沈建华, 彭晓晶
(1.南通大学 计算机科学与技术学院,江苏 南通 226019;2.华东师范大学 计算机科学与软件工程学院,上海 200062; 3.恩智浦半导体上海有限公司,上海 201203)
·实验技术·
简单有效的PID温控算法
胡传志1,沈建华2, 彭晓晶3
(1.南通大学 计算机科学与技术学院,江苏 南通 226019;2.华东师范大学 计算机科学与软件工程学院,上海 200062; 3.恩智浦半导体上海有限公司,上海 201203)
因为温度控制具有大时滞、大惯性的特点,以至于常规PID不能对其有效控制,所以一般需要采用具有参数自整定功能的自适应PID。不过,自适应PID的算法相对复杂,提高了使用与维护的难度,也增加了控制器成本。为此,设计并实现了一个简单有效的PID温控算法,该算法在常规PID算法的基础上做了两点改变,一是采用随温度变化趋势而变化的制动因子削弱大时滞的影响;二是采用随温度停滞时间而变化的积分速度因子调节积分速度,避免超调。该算法在一种旋转滴界面张力仪的温控系统中取得了不错的效果,为温控问题提供了简单有效的解决思路。
温度控制; 自适应PID; 制动因子; 积分速度因子; 旋转滴界面张力仪
0 引 言
温度控制是自动控制领域中一个重要话题,PID控制器因为结构简单、技术成熟、鲁棒性强等优点,而被广泛应用于控制系统中,据统计,PID控制器在实际控制系统中所占的比例超过90%[1]。但是常规PID难以应付温度控制过程中大时滞、大惯性的特点,业界一般采用模糊理论或神经网络对PID参数进行在线修正,形成自适应PID控制器来控制温度[2-10]。另外,西门子PLC中的PID温控程序采用了Astrom和Hagglund提出的继电型PID自整定方法[11]。当然,除了在线修正PID参数外,还可以使用模糊理论直接修正加热控制量[12]。
自适应PID或者涉及深奥的智能理论,或者涉及复杂的自整定方法,不仅提高了使用与维护上的难度,也增加了控制器的成本,这在硬件资源相对紧张的嵌入式系统领域,显得尤为不便。本文设计了一个简单有效的PID温控算法,该算法在一种旋转滴界面张力仪的温度控制系统中取得了不错的效果。
1 PID温控的加热过程
当以一定加热速度进行加热的同时也伴随着热流失,如果加热速度大于热流失速度,那么温度将升高,不过随着温度升高,热流失速度将加大[13],当热流失速度等于加热速度时,温度将保持不变。
图1所示的加热过程的开环阶跃响应貌似是一个稳态的过程,但是要经过很长时间之后才呈现稳态,超过了控制时效,在可接受的控制时效范围内看,该过程是发散的,是一个积分过程[14]。既然是一个积分过程,为了减小调节时间,应该在距离设定温度较远时采用快速加热,靠近设定温度时减小加热速度,直至到达设定温度时采用和该温度下的热流失速度相等的加热速度来维持设定温度。

图1 加热过程的开环阶跃响应
如果采用PID进行加热控制,加热速度由下式输出决定:
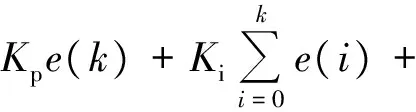
Kd(e(k)-e(k-1))
(1)
PID的输出是比例、积分和微分3个分量的线性组合,在加热过程中不管各分量如何变化并起作用,最终到达稳态时,因为偏差保持为0,所以只有积分分量在起作用,其他两个分量都是零输出。如此看来,完美的控制效果就是,开始时比例为主,积分为次,微分适时制动,随着距离设定温度越来越近,比例分量逐渐减弱,积分分量逐渐累加,当到达设定温度时,比例分量为0,积分分量正好等于所需控制量,这个控制量所产生的加热速度正好等于设定温度下的热流失速度,从而温度保持不变,有平衡关系式:
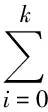
(2)
式中:I(k)为积分值;q(T)为热流失,是温度的函数。
但是,因为温度控制具大时滞、大惯性的特点,常规PID控制器没有根据现场情况随时调整增益参数的能力,导致无法对其实现有效控制,经常会出现以下情况:
(1) 积分不足。在到达设定温度时,积分分量远没有累加到平衡关系公式所要求的量。较大的比例分量的滞后作用使温度到达设定值,并非通过积分的微调作用。
(2) 积分过量。过快的积分速度使得到达设定温度时,积分分量大大超过平衡关系公式所要求的量。
自适应PID控制器通过对PID的参数进行在线修正,以避免上述情况。本文避开复杂的参数自整定方法,旨在设计一种简单的PID算法,针对上述两种情况对常规PID做以下两点调整:① 用制动因子替代微分分量,根据现场情况提供适时适当的制动,抑制比例分量的输出,尽量使得在积分分量接管加热任务时比例分量的作用已经不再是主要力量,避免因为比例分量的时滞作用引起的积分不足现象;② 用两个积分速度因子根据现场情况随时调节积分速度,避免积分过量现象。
2 简单的PID温控算法
2.1标识现场情况的元素
将现场情况归结为偏差、升温态、降温态和停滞态这4种元素:① 偏差:e(k);② 升温态:e(k)lt;e(k-1);③ 降温态:e(k)gt;e(k-1);④ 停滞态:e(k)=e(k-1)。
设计一个计数器n,如果当前PID控制周期处于停滞态,就将计数器n加1,以记录该温度的停滞时间。如果当前PID控制周期处于升温态或降温态,将计数器n初始化为1。
2.2制动因子
微分分量仅是根据泰勒级数的前两项来评估变化趋势,由此做出的制动,过于粗糙。于是采用制动因子代替微分分量,将PI控制器的计算结果乘以制动因子,用以对不同现场情况做出适当制动。将制动因子设为b,根据不同阶段、不同状态进行取值:
(1) 当e(k)lt;0时,此时已经超调,如果升温或降温时,取b=0,使控制量为0,采用最大制动;如果处于停滞态,取b=1,不制动。
(2) 当0≤e(k)≤L时,其中L是一个很小的常数,说明此时已经很靠近设定值,积分分量已经取代了比例分量的主导地位。为了控制的稳定性,需要取消制动,取b=1。
(3) 当Llt;e(k)时,此时尚未靠近设定值,如果处于停滞态,取b=1,不制动;如果处于降温态,取b为一个大于1的值,放大控制量,抑制降温;如果处于升温态,取b为上一轮温度停滞时间n的函数,停滞时间越小,制动越大,即b取较小的值,反之停滞时间越长,制动越小,即b取较大的值。可设为:
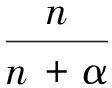
(3)
改变α可以调节制动强度,α越大,制动因子越小,说明制动越强,反而反之。
综合以上3种情况,不同阶段、不同状态下制动因子的取值情况参见表1。

表1 制动因子取值表
2.3积分速度因子
该算法结合使用传统的根据偏差值的变速积分方法和根据温度停滞时间的变速积分方法,将偏差乘以两个速度因子后再积分。
2.3.1根据偏差值的变速积分方法
偏差越大,积分速度越慢,反之则越快。积分速度因子与偏差的关系可设为[15]:
v1(e(k))=
(4)
Agt;0,Bgt;0
2.3.2根据温度停滞时间的变速积分方法
因为温度的变化很慢,通常在某个温度点,都要维持几个甚至几十个控制周期,这时若只考虑偏差大小而不考虑停滞时间,就不够精确了。为此,又设计了另一个积分速度因子,根据温度停滞时间决定速度快慢,开始时速度很慢,如果长时间仍然停留在该温度,就需要适当加快积分速度。和制动因子类似,可以设为:
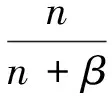
(5)
v2值在区间(0,1)内变化。v2随着n增大而逐渐增大。该方法看似合理,但是当n远大于β后,一直以接近1的速度进行积分,速度太快。如果把β取得太大,又迟迟不能消除静差。于是考虑将速度因子设为n的周期函数,周期为2β,可以设为:
(6)
v2值在区间[0,C]内周期变化,周期为2β。v2的平均值为:
(7)
由上式可见,v2的平均值由C值决定,C值越大,积分速度越快,反之越慢。β值决定了速度变化的平滑度,β越大,越平滑。
2.4根据设定值修改PID参数
根据平衡关系式,当设定温度较大时,需要较大的稳态下的控制量输出抵消较大的热流失,此时使用较大的积分系数可以降低对积分值的需求量,等于降低了调节时间。另外当设定温度较大时,使用较大的比例系数可以加大比例分量的作用,从而加快响应速度,减少调节时间。可将这个两个系数取为设定温度SP的一次函数:
Kp(SP)=k1·SP+b1
(8)
Ki(SP)=k2·SP+b2
(9)
2.5PID算法描述
根据以上所述,调整后的PID计算公式为:
u(k)=b(n)(Kp(SP)e(k)+Ki(SP)
(10)
算法流程如图2所示。当偏差较大时,不采用PID,如果小于设定值就全速加热,如果高于设定值就不加热;以此加快响应速度。

图2 算法流程图
2.6基于平衡关系式的参数整定方法
该算法抓住平衡关系式所表达的稳态时PID控制器的积分分量所产生的加热速度正好等于热流失这个要点,调试时通过比较第一次到达设定值时的积分值和稳态时的积分值的大小关系,容易知道制动因子和积分速度因子的参数设置是否合理,从而调节相应参数,使第一次到达设定值时的积分值尽量靠近稳态时的积分值。如果是积分不足,说明制动比较弱,是比例分量的滞后作用将温度加热到了设定值,而非积分分量的微调作用,通过加大制动因子中的参数α来增强制动作用;如果是积分过量,说明积分速度过快了,通过减小速度因子中的参数C来调低积分速度。
3 实 验
3.1实验平台
这种旋转滴界面张力仪的温控系统结构框图如图3所示,PID控制器输出的PWM信号的脉宽决定了一个周期内固态继电器SSR的导通时间,从而控制电热丝的加热功率。实验中将PWM信号的周期取为1 s,脉宽取值范围是0到1 000,如果忽略固态继电器的导通与截至时间,这样的设计便可以产生0、1、2、……、1 000等1 001种不同的加热功率。反馈部分采用热敏电阻感知温度,电阻两端的电压值随温度而变化,经过低通滤波、模数转换以及温度转换函数得到当前温度值,形成闭环控制。该系统的性能指标为:温控范围在[室温,90.0℃],调节时间≤40 min,稳态误差≤0.2 ℃,超调量≤1.0 ℃。
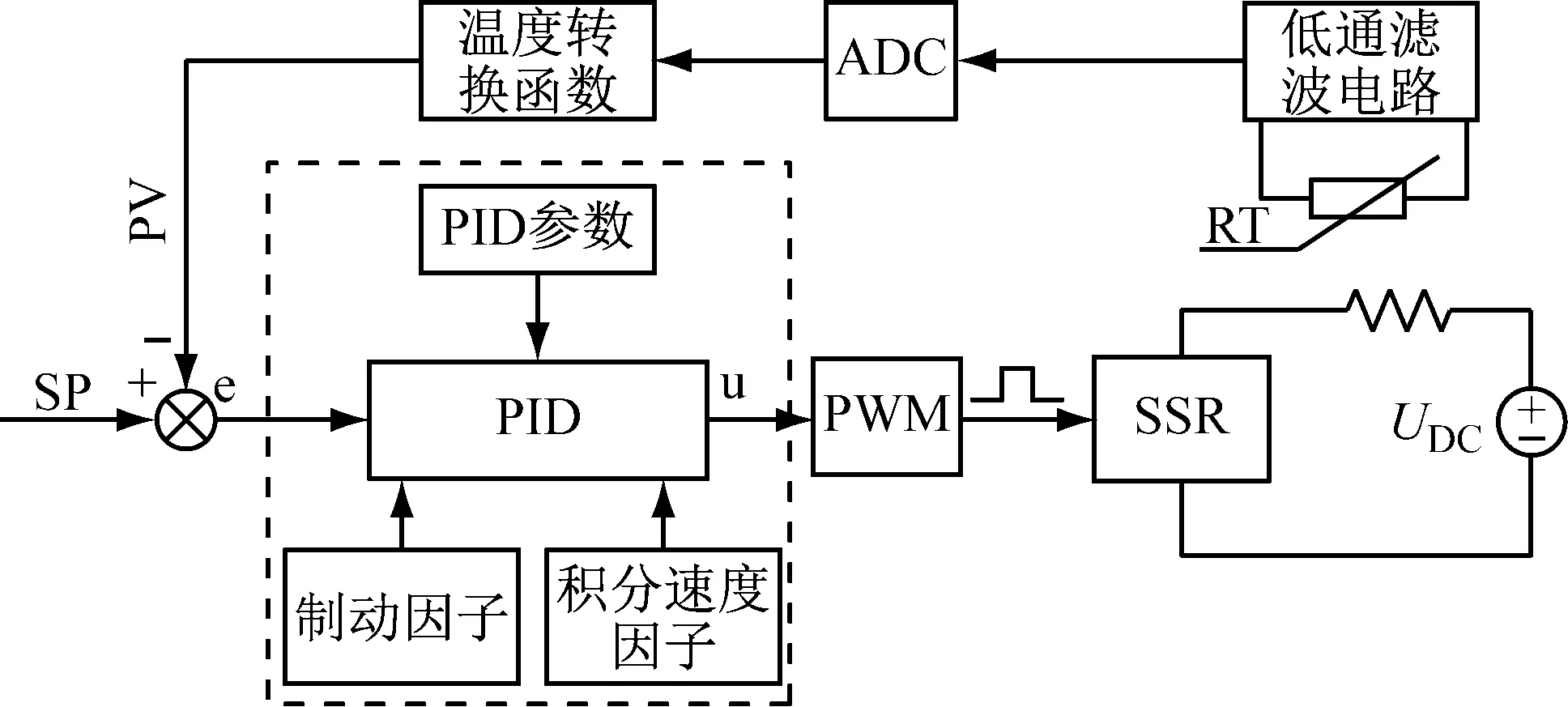
图3 温控系统结构图
3.2实验及分析
工程应用中,为了便于存储和计算,将浮点型温度值乘10后取整。实验中的各参数设置如下:
(1) PID参数,k1=10-2,b1=6,k2=10-4,b2=0.02。
(2) 制动因子参数,α=6.0。
(3) 积分速度因子参数,A=65,B=5,C=0.8,β=20。
将温度从16.0 ℃依次加热到37.5 ℃、50.6 ℃和68.8 ℃,以及从16 ℃加热到81.8 ℃,4个加热过程的指标数据见表2,完全满足系统的性能指标要求。
因为到达设定值时候的积分值和稳态时候的积分值很相近,所以有较好的性能指标,这说明制动因子和积分速度因子的参数设置是合理的。如果将制动因子的参数α改为1.0,减小制动效果的话,将会出现积分不足的情况;如果将积分速度因子的参数C改为1.0,加快积分速度的话,将出现积分过量的情况。使用这两种改动后的参数,将温度从16.0 ℃加热到37.5 ℃,前者可以到达稳态,只是调节时间太长;后者不仅超调,而且会震荡,两个加热过程的指标数据见表3。
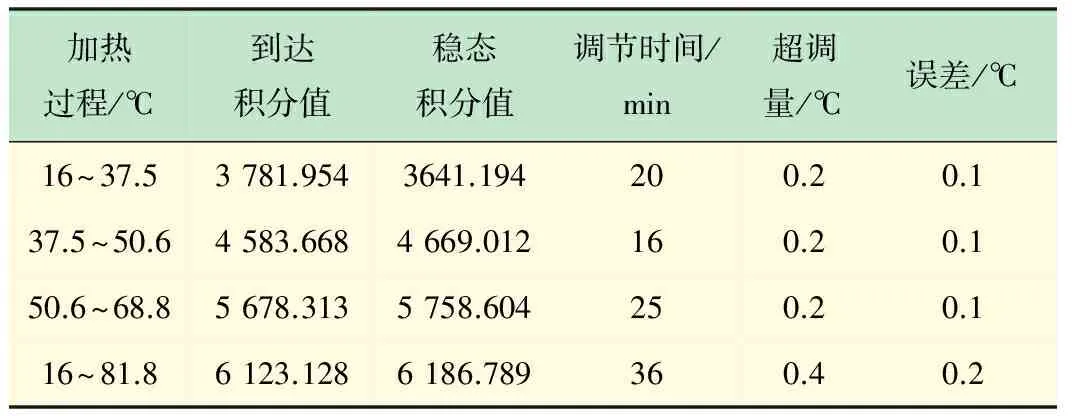
表2 正常加热过程的指标数据表

表3 积分不足和积分过量的加热过程指标数据表
以上实验说明,基于平衡关系公式所阐述的原理,通过比较到达时的积分值和稳态时的积分值的大小,很容易判断制动因子和积分速度因子的参数设置是否恰当,这为参数整定提供了简单的方法。当然,过大的比例系数和积分系数也会导致积分不足的情况,这里不再赘述。
为了进一步说明本方法的有效性,图4给出了使用该简单PID算法和使用西门子自适应PID温控程序将温度从16.0 ℃加热到37.5 ℃的阶跃响应曲线的比较。相比之下,虽然该方法的调节时间稍慢了些,但是相比于拥有1 400行的西门子温控程序,该算法仅有73行代码,仅用到了正弦函数,从而极大减少了控制器的存储和计算成本。

图4 两种算法的阶跃响应比较
4 结 语
本文成功设计并实现了一个简单有效的PID温控算法,并给出了简单的基于平衡关系公式的参数整定方法。该算法应用于一种旋转滴界面张力仪的温控系统中,取得了和西门子自适应PID温控程序相近的效果,相对于这些基于模型、规则或智能理论等进行参数自整定的PID算法,该算法不仅降低了使用和维护的难度,还节约了控制器资源,这一点对于资源相对紧张的嵌入式控制系统来说具有一定的实用意义,也符合智能控制设计中的基本策略——“简单性”[16]。
[1] KNOSPE C.PID control[J].IEEE Control System Magazine,2006,26(1):30-31.
[2] 李敏远,都延丽,姜海鹏.智能自整定PID在药剂温度控制系统中的应用[J].控制理论与应用,2003,20(5):805-810.
[3] 谭宝成,成法坤.自适应模糊PID在中频弯管机温度控制中的应用[J].西安工业大学学报,2010,30(2):191-195.
[4] 任朝晖,王永富,闻邦椿.闪蒸干燥机温度的自适应模糊PID控制[J].控制工程,2006,13(1):22-24.
[5] 程 越,程文明,郑 严.基于自适应模糊PID的中药提取温度控制[J].控制工程,2009,16(5):527-530.
[6] 黄邵川.基于模糊PID大型电力机组温度过热控制[J].控制工程,2014,21(6):1006-1010.
[7] 余 尧,王先全,朱桂林,等.基于BP 神经网络自整定的PID 温度控制系统的设计[J].电子器件,2015,38(6):1360-1363.
[8] 姜文佳,姜永健,姜广田,等.模糊PID控制算法改进及在温控系统中的应用[J].控制工程,2006,13(4):338-340.
[9] 赵红艳.基于参数自整定模糊PID的飞机液压能源油温控制[J].计算机测量与控制,2014,22(5):1404-406.
[10] 徐晓冬,徐晓辉,任安业.基于参数自整定模糊PID控制的大型液压源温控系统设计[J].上海航天,2010(5):60-64.
[11] 曾喜娟,庄其仁,吴志华.基于S7-200 PLC的PID参数自整定方法[J].组合机床与自动化加工技术,2010(1):47-50.
[12] 王 伟,吴 敏,曹卫华,等.基于组合灰色预测模型的焦炉火道温度模糊专家控制[J].控制与决策,2010,25(2):185-190.
[13] Franklin G F, Powell J D, Abbas Emami-Naeini.自动控制原理与设计[M].6版,北京:电子工业出版社,2014.
[14] Astrom K J, Hagglund T.PID controllers:Theory,desing and turnig[M].2 ed.North Carolina: Instrument Society of America,1995.
[15] 刘金琨,先进PID控制Matlab仿真[M].3版.北京:电子工业出版社,2011.
[16] 胡包钢,应 浩.模糊PID控制技术研究发展回顾及其面临的若干重要问题[J].自动化学报,2001,27(4):567-584.
ASimpleandEffectivePIDControllerforTemperatureAdjustment
HUChuanzhi1,SHENJianhua2,PENGXiaojing3
(1.School of Computer Science and Technology, Nantong University, Nantong 226019, Jiangsu, China;2.School of Computer Science and Software Engineering, East China Normal University, Shanghai 200062, China;3.NXP Semiconductors Shanghai Co., Ltd., Shanghai 201203, China)
Usually, adaptive PID is used to supersede conventional PID in temperature control system because of large time-delay and large inertia.However, adaptive PID with complex self-turning function brings the difficulty for user and increases the cost of microcontroller.For this reason, this paper presents a simple and effective PID controller.The controller utilizes the braking factor that complies with the temperature trend to weaken the impact of the time-delay, utilizes the integrated velocity factor that complies with the delay time to avoid overshooting.It was proved that the PID controller achieved good effect in the temperature control system of a spinning drop tensiometer.The PID controller provides a simple and effective solution to control temperature.
temperature control; adaptive PID; braking factor; integrated velocity factor; spinning drop tensiometer

TP 273.5
A
1006-7167(2017)10-0004-04
2016-12-29
国家自然科学基金项目(41301514)
胡传志(1977-),男,江苏徐州人,硕士,高级实验师,研究方向为嵌入式系统和自动控制。Tel.:13515209092; E-mail:hubanxian@ntu.edu.cn
