基于MATLAB的多目标规划问题的理想点法求解
2017-12-12杨伍梅刘陶文
杨伍梅,刘陶文
基于MATLAB的多目标规划问题的理想点法求解
杨伍梅1,刘陶文2
(1. 益阳职业技术学院基础课部,湖南 益阳 413049;2. 湖南大学数学与计量经济学院,长沙 410012)
针对生产、经济活动等实际中常见的多目标规划问题,在对现有的多目标优化方法进行一些比较的基础上,重点对理想点法的基本思想、特点及发展过程进行了探究,并就工厂采购这类多目标规划的实际问题采用理想点法进行模型的构建、转化和求解,然后用MATLAB软件对此问题进行了具体计算和结果分析﹒结果表明这类方法具有非常简单、实用、高效的特点,在实际应用中具有一定的优越性﹒
多目标规划;评价函数法;理想点法;MATLAB
在生产、经济活动、工程设计和科学实验中,往往需要同时考察多个指标才能判断某种决策(计划、方案、配方)的优劣,这些问题可归结为多目标规划问题[1]﹒最初,关于多目标问题中如何协调矛盾是由Franklin于1772年提出的,而第一次从数学角度提出多目标规划问题并且给出Pareto最优解的概念的是Pareto﹒同时Kuhn等人也给出了向量极值问题具备有效解的必要条件﹒后来,A.Charnes等人做了许多工作,出现了如加权和法、目标规划法、-约束法等多目标优化方法[2]﹒我国对于多目标规划问题的研究主要是从20世纪70年代开始的,且研究的人越来越多,已逐步迈向世界先进水平[3]﹒当前,关于多目标规划问题的研究,主要着重于其解的概念与性质、求解方法、对偶问题、不可微等4个方面,其中研究最多的是关于多目标规划的求解方法问题﹒近年来引用次数较多,涉及知识面较广的方法有最小偏差指标赋权法、加权偏差平方和最小化方法、线性加权法和灰色关联分析法的集成法等﹒
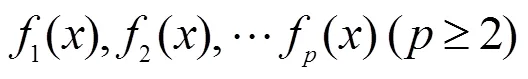

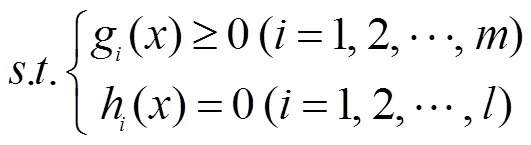
对上述多目标规划问题的求解目前主要有约束法、功效系数法和评价函数法等方法﹒约束法要根据决策者的经验让次要目标在某一确定的范围内取值,所以其结果受人为因素影响较大[4]﹒功效系数法能较好的求解多目标规划问题,但往往会因为信息的非完备性和主观判断等因素导致功效系数不是很准确,从而影响求解结果[5]﹒因此这里主要采用评价函数法来求解多目标规划问题,它的基本思想是由多目标规划问题的目标函数构造出某一个单目标规划问题的目标函数,并称之为评价函数[6],从而将求解多目标规划问题化为求解单目标规划问题﹒由于构造评价函数时可用多种不同的方法,因此就有多种不同的评价函数法,其中最常见的评价函数法有理想点法、平方和加权法、线性加权和法和乘除法等[7]﹒文献[8]采用平方和加权法和线性加权和法、乘除法对采矿法多目标优选进行了探讨,取得了较好的效果,但该方法需要根据各个目标的重要程度给予一组适当的权重,而在实际应用中要选取这样一组权重往往存在一定的困难,所以只能假设在某种权重下进行计算,这样会因所假设权重的不同而导致结果与实际问题存在一定偏差﹒为了避免个人选取权重的片面性,往往采用老手法选取权重,但这项工作量比较大﹒乘除法原理简单,计算方便,不需要考虑各个目标的权重受人为因素的影响较小,但它要求目标函数在已有条件下的函数值都具有非负性,且要分为目标函数值越小越好与目标函数值越大越好两组,因此在实际应用中具有一定的局限性[9]﹒在文献[10]中郭惠昕等人将理想点法用到多目标模糊优化设计中,由正、负理想点与可行解之间的距离构造出模糊判决,并由此提出了基于理想点的求解算法,但此法在工厂采购问题方面未见有关研究,本文主要采用理想点法对工厂采购问题进行一些探讨﹒
1 理想点法
理想点法是指根据决策者的先验信息构造出理想点,再在指定条件下去寻求与此理想点最为接近的可行解[11]﹒在实际情况中,问题本身可能含有多个不等式约束条件和多个等式约束条件,但在实际问题中刚好满足等式约束条件的问题局限性较大﹒因此,本文只针对式(2)的仅含有不等式约束的多目标优化问题进行探讨﹒
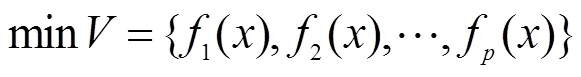

根据评价函数法的基本思想,理想点法的主要思路是在多目标规划问题(见式(2))中,首先将多目标规划问题分解为个单目标规划问题,可得表达式(3)﹒


求解单目标规划问题(见式(4))就可以得到兼顾多个目标的满意解﹒
2 实例
2.1 工厂采购问题
某工厂需要采购某种生产原料,该原料市场上有A、B、C三种,单价分别为3元/kg、2元/kg、4元/kg﹒现要求所花的总费用不超过400元,所购得的原料总质量不少于150 kg,其中A原料不得少于40 kg,B原料不得少于50 kg,C原料不得少于20 kg﹒问如何确定最佳采购方案,花最少的钱采购最多数量的原料﹒
2.2 建立模型

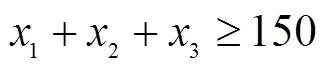
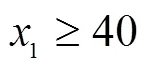
综合以上分析得最优化数学模型见式(6)﹒
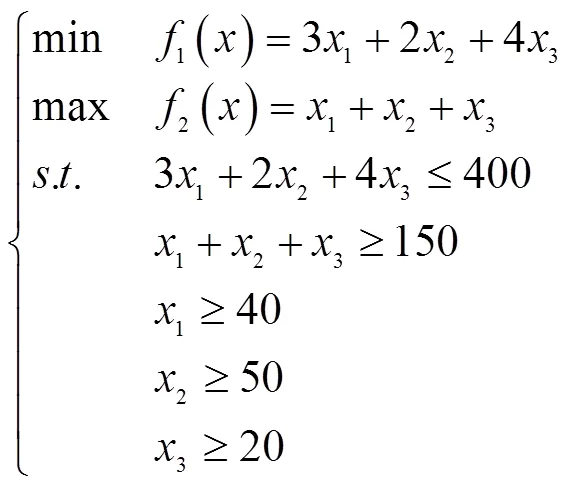
2.3 模型转化与求解
注意到在多目标规划问题中极大化目标函数是极小化目标函数的相反数,因此,上述最优化数学模型式(6)可以转化为标准形式式(7)﹒

很明显,这是一个多目标规划问题,可以采用约束法、功效系数法和评价函数法等方法进行求解﹒本文采用评价函数法进行求解,即根据理想点法的求解思路,可将上述问题分解为两个单目标规划问题(P1)和(P2)进行求解,见式(8)﹒
2.4 实值求解与结果分析
由模型(P1)可以看出,它的评价函数为一个线性函数,且约束条件也为线性函数,所以可以利用MATLAB优化工具箱中所提供的linprog函数进行求解,其运行代码和结果如下:
>>=[3;2;4];
=[2,3,4;-1,-1,-1];
=[400;-150];
=[40;50;20];
>>[,fval]=linprog(,,,[],[],);
Optimization terminated.

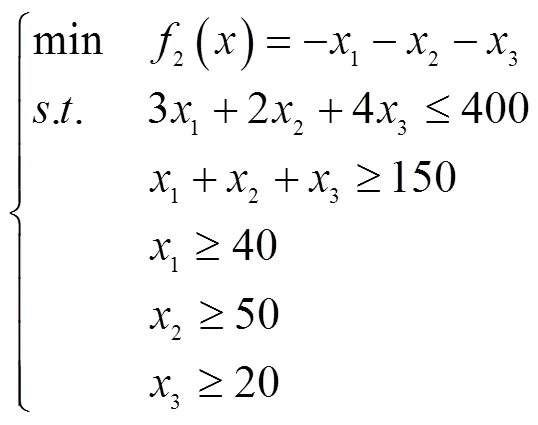
60.000 0
20.000 0
fval=410.000 0
采用类似方法可求解单目标规划问题(P2),利用MATLAB软件求解,其运行代码和结果如下:
>>=[-1;-1;-1];
=[2,3,4;-1,-1,-1];
=[400;-150];
=[40;50;20];
>>[,fval]=linprog(,,,[],[],);
Optimization terminated.
50.000 0
20.000 0
fval=-155.000 0

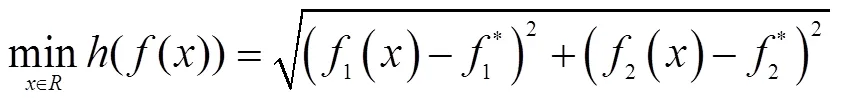

利用MATLAB软件求解,其运行结果如下:
59.615 4
20.000 0
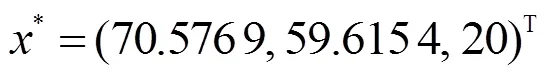
3 结论
多目标规划在生产、经济活动、科学实验和工程设计中有着非常广泛的运用,但多目标规划在实际应用过程中,由于存在多个目标,要求各目标同时取得较优的值,从而使得求解的方法与过程都相对复杂﹒利用理想点法将多目标规划问题化为单目标规划问题,借助MATLAB软件计算可以达到对多目标规划问题求解更为简便、高效、准确的目标,从而可将此问题推广到更高维的情形,也可以将此方法推广到更多领域,更好地利用多目标规划解决实际问题﹒
[1]刘文奇, 余高锋, 胥楚贵. 多目标决策的激励策略可行解[J]. 控制与决策, 2013, 28(06): 957-960.
[2]艾正海. 关于多目标决策问题的理想点法研究[D]. 成都: 西南交通大学, 2007.
[3]杨桂元, 郑亚豪. 多目标决策问题及其求解方法研究[J]. 数学的实践与认识, 2012, 42(2): 108-115.
[4]万嘉滢, 张雯, 单莹. 一种改进多目标规划逐步Stem与妥协约束法及应用[J]. 统计与决策, 2013(14): 79-81.
[5]罗晓光, 刘飞虎. 基于功效系数法的商业银行财务风险评价研究[J]. 科技与管理, 2012, 14(05): 93-98.
[6]郭丽暄. 关于多目标规划的评价函数法[J]. 漳州职业技术学院学报, 2006, 8(04): 12-15.
[7]陈国华, 廖小莲. 多目标投资组合模型的理想点解法[J]. 湖南工业大学学报, 2010, 24(1): 47-49.
[8]陈灿. 基于组合赋权-理想点法的顶底柱开采方案优选研究[J].矿业工程, 2015, 23(03): 15-18.
[9]郭金维, 蒲绪强, 高祥, 等. 一种改进的多目标决策指标权重计算方法[J]. 西安电子科技大学学报: 自然科学版, 2014, 41(06): 118-125.
[10]郭惠昕, 张龙庭, 罗佑新, 等. 多目标模糊优化设计的理想点法[J]. 机械设计, 2001, 18(8): 18-20.
[11]杨伍梅, 刘权. 基于MATLAB的多目标规划最优投资组合方法的探讨[J]. 长沙大学学报, 2014, 28(05): 9-11.
(责任编校:龚伦峰)
Research on the Ideal Point Method of Multi-objective Programming Based on MATLAB
YANG Wumei1, LIU Taowen2
(1. Department of Basic Courses, Yiyang Vocational and Technical College, Yiyang, Hunan 413049, China; 2. School of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410012, China)
The common multi-objective programming problems in production and economic activities are analyzed in this paper. The basic idea, feature and development process of the ideal point method on the basis of comparing, the exising multi-objective optimizing methods are investigated. Based on the ideal point method, the model construction, transformation and solution of the multi-objective planning of the factory procurement are executed, and then the problem is calculated and analyzed with MATLAB. Experimental results show that the proposed method is simple, practical and highly efficient, and outperforms the classical multi-objective programming methods.
multi-objective programming; evaluation function method; ideal point method; MATLAB
O1
A
10.3969/j.issn.1672-7304.2017.04.0013
1672–7304(2017)04–0060–04
2017-06-18
湖南省教育厅科研项目(15C1382)
杨伍梅(1981- ),女,湖南益阳人,讲师,硕士,主要从事最优化理论与算法研究﹒E-mail: 40748054@qq.com
