“联通‘HL’”的勾股定理

王钰婷

由于提前预习了勾股定理的内容，我对勾股定理的新课没什么特别新奇的感觉，在我看来，勾股定理就是为确定直角三角形的三边平方关系，即为“在直角三角形中，已知两边求第三边”带来了方便.但上课时，我却被勾股定理的强大“联通”能力所折服了.老师的板书也很有特点，下图是我抄录的部分板书：

板书中的“应用”与“关联”都好理解，但是课堂小结时，老师还补充了一个思考题：“HL”为什么是定理？定理必须要有证明的.我常常喜欢挑战老师在课堂上提到的這些“思考问题”，以下就是我的一些“研究”成果.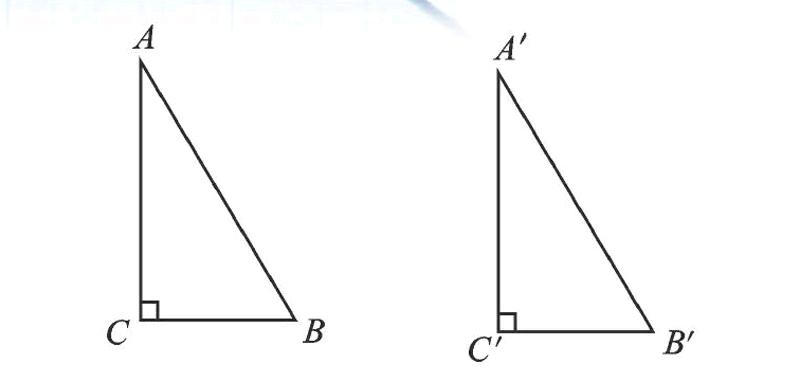

对“HL”定理的证明：

已知：如图，在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，AB=A′B′，AC=A′C′.

求证：Rt△ABC≌Rt△A′B′C′.

证明：在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，根据勾股定理，得BC2=AB2-AC2，B′C′2=A′B′2-A′C′2.又AB=A′B′，AC=A′C′.∴BC=B′C′.∴△ABC≌△A′B′C′（SSS）.

解后思考：看来勾股定理真是很强大，连以前我们没有证过的“HL”也能被轻松转化成“SSS”.

教师点评：学习全等三角形的判定方法时，“SSS”“SAS”“ASA”这3个判定方法是告知学生基本事实（类似“公理”，不需要证明）.但“AAS”是由“ASA”推广得出的，所以称之为定理，后来，教材上又利用作图确认了“HL”定理，但是没给出证明.数学是追求严谨的，如果一个定理的出现，不“立即”跟进证明，自有其“难言之隐”，因为“知识储备”还不足.上文中小作者结合勾股定理对“HL”进行的证明，其实就解释了当初我们为什么没有“立即”证明的“苦衷”.

学习或研究数学的经验（有时也是教训）表明，对于有些数学问题如果暂时不能解释清楚、严谨证明，并不影响我们“向前走”，或许在走过一段之后，手头多了新工具、新方法，蓦然回首，原先那个难题就可以迎刃而解了.想来，当我们“难求甚解”时，也许“不求甚解”也是可以容许的吧！

（指导教师：刘东升）endprint