城市地下道路分(合)流匝道通风阻力特性

袁浩庭， 陈 超, *， 李 琼, 2， 王陆瑶， 李亚茹

(1. 北京工业大学建筑工程学院， 北京 100124； 2. 华北科技学院建筑工程学院， 北京 101601)

城市地下道路分(合)流匝道通风阻力特性

袁浩庭1， 陈 超1, *， 李 琼1, 2， 王陆瑶1， 李亚茹1

(1. 北京工业大学建筑工程学院， 北京 100124； 2. 华北科技学院建筑工程学院， 北京 101601)

为分析多点进出结构的城市地下道路空气流动特性，以长沙市营盘路湘江隧道为原型，通过现场实测、缩尺模型试验以及CFD软件数值模拟方法，对分(合)匝道通风阻力特性进行了研究，考察了雷诺数、风量比、分岔角度对分(合)流匝道阻力特性的影响规律。研究结果表明： 1)主隧道与匝道风量比、主隧道与匝道夹角是影响分(合)流匝道局部阻力系数的关键因素； 2)城市地下道路分(合)流匝道局部阻力变化特性，不宜简单套用通风管道的三通构件的参数； 3)结合最小二乘法和Matlab软件对计算结果进行多因素回归分析，给出了基于长沙营盘路湘江隧道的分(合)流匝道主隧道和匝道的局部阻力系数关联式。研究结果可为复杂结构城市地下道路通风系统阻力特性分析及通风工程优化设计提供方法参考。

多点进出城市地下道路； 分(合)流匝道； 局部阻力系数； 缩尺模型实验； 数值模拟

0 引言

为缓解城市用地紧张、城市中心区主干道交通拥堵、缩短城区间的道路里程，多点进出城市地下道路已成为目前我国城市地下道路建设的主要隧道形式。例如，中国深圳新经济特区前海正在新建的一条穿越CBD区域的长约5.257 km的城市地下道路，沿线设置9个进出地面匝道的出入口、10个进出地下匝道的出入口。复杂的隧道结构特征，直接影响城市地下道路通风工程设计，特别是分(合)流匝道通风阻力特性会对多点进出城市地下道路空气流动特性产生直接影响。

关于隧道局部构件阻力特性的研究主要集中在公路隧道。李峰[1]对公路隧道弯曲风道进行了研究，得到了弯曲风道局部阻力损失系数随弯曲半径与隧道当量直径的关系； 温玉辉[2]采用数值模拟的方法对影响短道流态的4个因素(排风道与隧道轴线夹角、送风方向与隧道轴线夹角、送排风口间距和送排风流量比)进行单独分析； 喻映华等[3]通过数值模拟的方法对隧道紧急停车带的局部阻力系数进行了研究。同时部分学者对隧道三通局部阻力损失做了相关研究。石平等[4]结合《雁门关公路隧道运营通风与防灾技术研究》，采用理论分析、现场测试及数值模拟等方法，对三通局部阻力损失、送排风短道的优化进行了研究，得到了一系列有益于通风设计的结论； 马佳[5]运用数值模拟方法对影响公路隧道三通局部阻力系数的因素进行了研究，发现倾斜角度、主支流量比等因素对局部阻力系数有影响； 苟红松等[6]利用理论计算对隧道施工通风分风三通位置的选择做了研究，发现主风管与分风管直径比是影响风管出口风量的关键因素。国内外关于三通局部阻力损失相关的研究大多集中在管道三通局部构件上。COSTA等[7]对夹角为90°的三通局部阻力系数进行了研究，分析了雷诺数和流量比对局部阻力系数的影响； Abdulwahhab等[8]对夹角为90°的三通的局部阻力损失进行了模拟和试验研究，结果表明流量比对其阻力损失影响很大； 我国的很多学者也对管道三通局部阻力特性进行了研究[9-12]，分析了分流比、雷诺数、管间夹角和管径比等因素的影响。

目前，国内关于多点进出城市地下道路通风系统基础数据取值多是来自参考文献[13]，其关于支管与主管夹角对管道空气流动的影响，仅仅给出了夹角为30°、45°和90°时的3种情况； 现行规范[14]涉及到多点进出隧道主隧道与分(合)流匝道夹角对隧道空气流动的影响，也只是给出了夹角为90°时的情况。考虑到实际隧道工程分(合)流匝道与常见通风三通管道的不同性，以及实际隧道主隧道与分(合)流匝道角度通常都小于30°的实际情况，本文以多点进出城市地下道路的分(合)流匝道通风阻力特性为重点研究对象，通过现场实测、缩尺模型试验和数值模拟的方法，研究并分析雷诺数Re、主隧道与分(合)流匝道风量比q、主隧道与分(合)流匝道夹角θ等因素对分(合)流匝道局部阻力系数的影响规律，以期为城市地下道路通风系统设计提供参考。

1 材料与方法

1.1 缩尺模型试验

1.1.1 试验台搭建

长沙市营盘路湘江隧道(以下简称长沙隧道)位于长沙市中心城区，为双洞单向隧道，由南线和北线2条独立且平行的隧道构成，主线为双车道、总长2.7 km，每条隧道均有2个入口和2个出口，其中东侧出(入)口对接湘江东岸商业区，西侧出(入)口对接湘江西岸居住区，如图1所示。 其中，A匝道长648 m、B匝道长425 m、C匝道长632 m、D匝道长752 m，均为单车道。匝道虽为单车道，但同时考虑了1条应急车道，因此主、匝隧道断面尺寸几乎一样。主、匝道断面结构尺寸见图2。

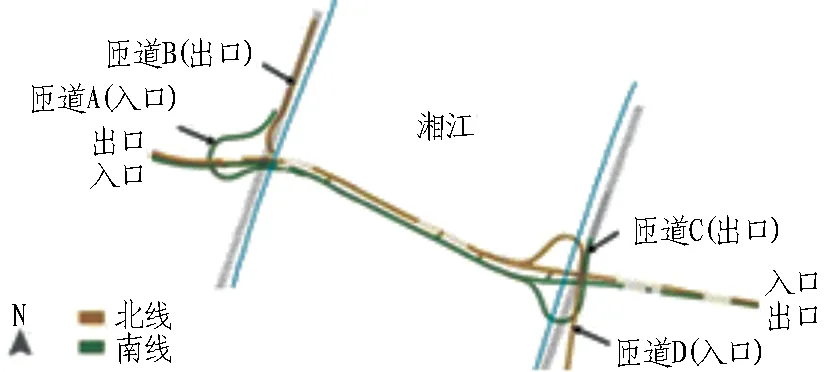
图1 线路示意图

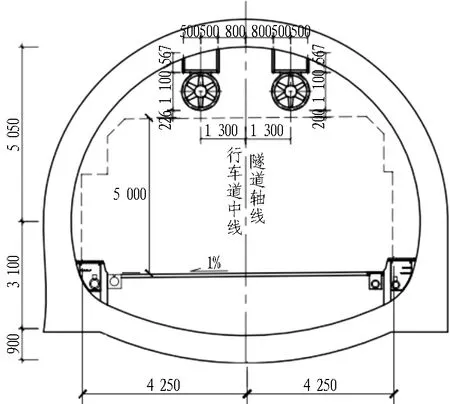
(a) 主隧道断面构造图

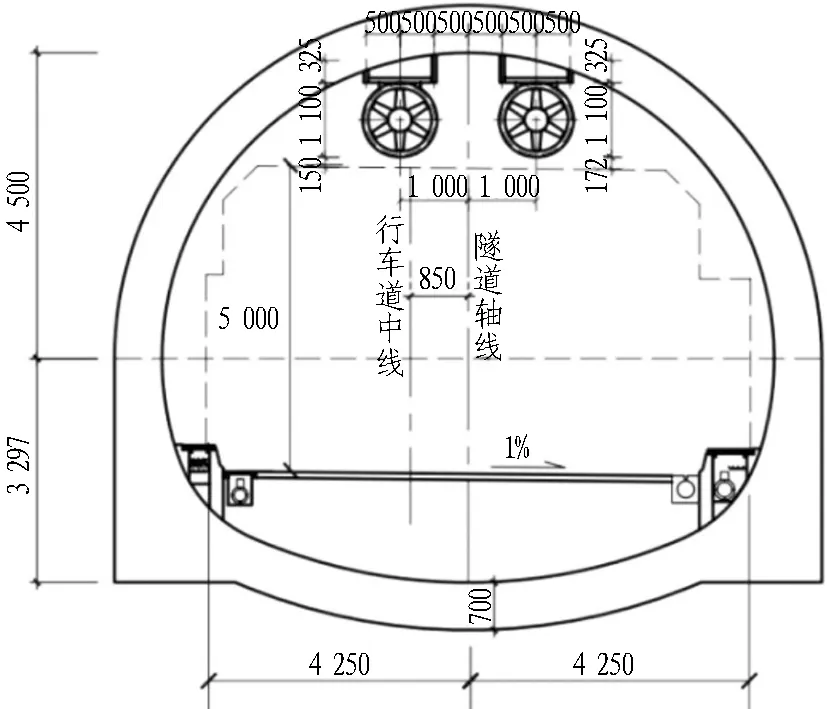
(b) 匝道断面构造图

根据流体力学理论以及流动相似理论，本文以长沙隧道为原型，基于雷诺相似准则和几何相似准侧搭建1∶8缩尺模型比例试验台，试验台尺寸见表1。

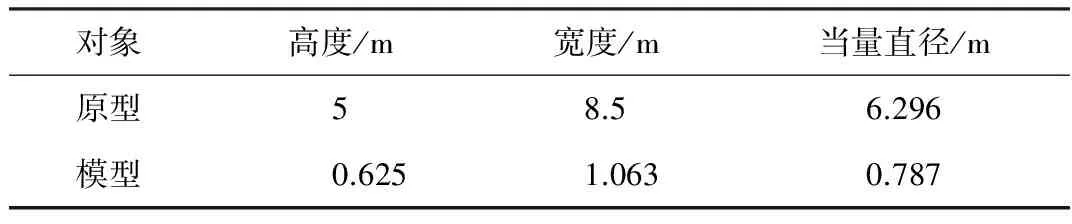
表1 模型试验台尺寸

考虑到实际隧道通风速度通常都在紊流区，雷诺数Re>5×104，满足自模区的要求，因此主要考虑在几何相似和边界条件相似的前提下，使模型的空气流动充分发展成完全紊流，进入阻力平方区，即自动模型区，确保与原型流动保持相似。基于管内自模区临界雷诺数大于5×104，且可适当降低的设计原则[15]，模型试验最小风速按0.69 m/s，对应临界雷诺数Re>3.5×104。

按照几何相似准则，试验场地无法满足模型长度要求。为此，本研究采用变态模型法对模型的长度进行补偿修正，且将变态率控制在4以内。变态率

k=CL/CD=4[15]。

(1)

式中：k为变态率；CD为径向比尺，CD=DP/Dm(DP为原型当量直径，Dm为模型当量直径)，本试验台为8；CL为长度方向的比尺，CL=LP/Lm(LP为原型长度，Lm为模型长度)。

根据式(1)，模型长度虽可缩短到2 700/32=84.37 m，但试验场地仍然难以满足要求。因此进一步采用等效模拟法，即加阻力格栅的方式，以局部阻力代替沿程阻力，对模型长度进行补偿修正。试验模型的最终长度为30 m。

图3为1∶8模型试验台示意图，试验台主要由风机、软连接、整流段、格栅段、主隧道段、变径段和匝道段等组成。其中变径段长5 m，风管材料采用镀锌板。

图3 1∶8缩尺隧道模型试验台

1.1.2 测点布置及数据采集

缩尺试验台各功能段构成及其风速、风压等参数采样点位置如图4所示，风速、风压测试仪器以及通风机等性能参数见表2，各采样点位置按照上游大于2倍当量直径、下游大于3～5倍当量直径的原则确定。分流试验时，主隧道风机正转； 合流试验时，主隧道风机反转。当主隧道风速稳定后，采集各个采样点的风速和风压，风速每20 s采集1次，连续采集30 min； 风压每5 min采集1次，采集30 min，共采集6组数据。

图4 分(合)流段通风试验测点布置图

Fig. 4 Layout of monitoring points for ventilation of confluence and distributary sections

1.2 数值计算分析

1.2.1 物理模型及网格划分

根据图5建立相应的CFD计算物理模型，采用Gambit软件建立相应的结构型网格模型，如图6所示。通过网格独立性检验，模型长度方向(z轴方向)、宽度方向(x轴方向)和高度方向(y轴方向)的网格尺度分别为0.1、0.062 5、0.062 5 m； 总网格数为55 250个。

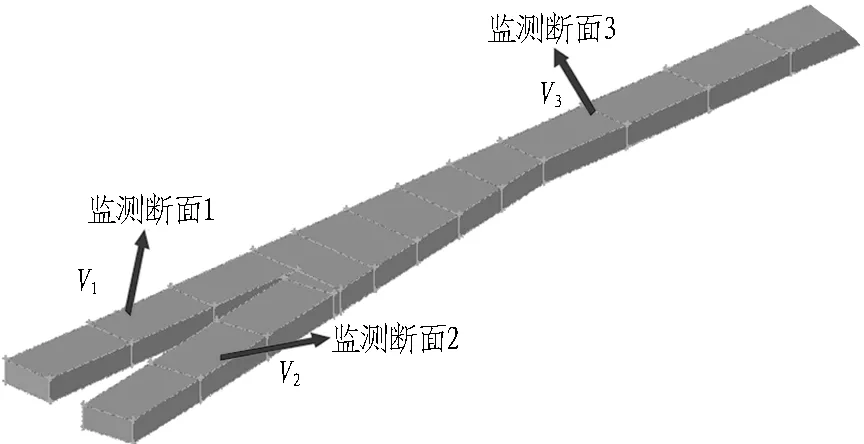
图5 计算物理模型

图6 网格模型

1.2.2 模拟工况

根据长沙隧道不同工况下的实测结果，直隧道通常风速为2～7 m/s，支隧道风速为1～4 m/s。为考察雷诺数、风量比(包括上下游主隧道的风量比q1以及上游主隧道与匝道的风量比q2)以及主隧道与匝道的夹角等因素对分(合)流匝道局部阻力特性的影响规律，本研究分3种工况进行分析讨论，具体工况见表3。

表3 计算工况

1.2.3 模型计算及求解

1)模型求解条件。应用Fluent15.0软件对分(合)流匝道局部阻力系数进行分析。采用k-epsilon(2eqn)湍流模型，方程的离散采用有限体积法，扩散项采用中心差分格式离散。为提高计算精度，对流项采用二阶迎风格式离散，速度与压力的耦合计算采用SIMPLEC 算法。

2)边界条件。进出口条件： 设置速度入口或速度出口边界，采用湍流强度和水力直径定义湍流，采用压力出口或压力入口边界条件； 壁面条件： 固体壁面上采用无滑移条件，当量粗糙度为1 mm。

3)计算流体条件。空气温度为303 K、密度为1.225 kg/m3、动力黏度为1.789 4×10-5kg/(m·s)。

1.2.4 模型有效性验证

依据流体力学理论，风道构件局部阻力系数

ξ=Δp/p。

(2)

式中：ξ为局部阻力系数； Δp为2个测点之间的全压差；p为主隧道动压。

图7示出分(合)流匝道局部阻力系数与风速的关系图，是模拟结果的有效性验证，分岔匝道和合流匝道(θ=0°)局部阻力系数计算值与试验结果具有较好的一致性。

2 结果及分析

2.1 雷诺数的影响(工况1)

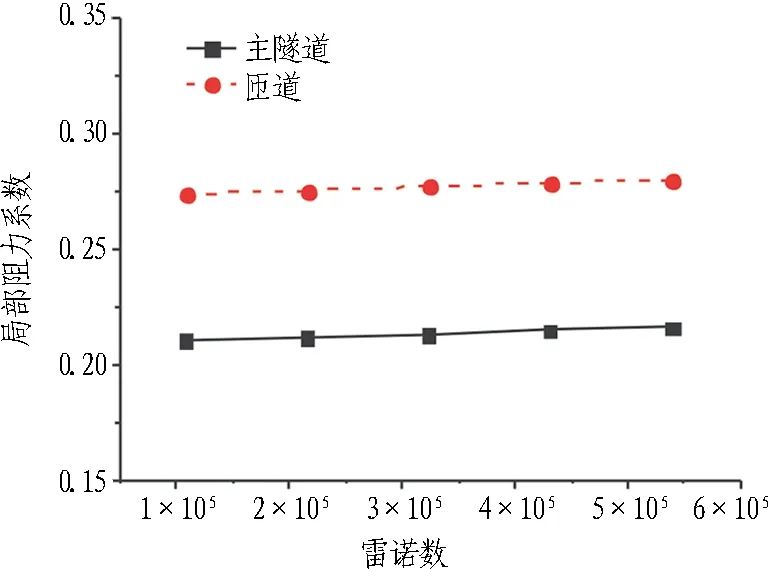
图8示出风量比q1=q2=0.5、主隧道与匝道夹角θ=0°时，主隧道风速变化对分流匝道、合流匝道局部阻力系数的影响有限，局部阻力系数变化很小。说明当流动处于紊流状态即阻力平方区时，局部阻力系数不再随Re变化。巩启涛等[9]发现，对于三通局部阻力系数，进入局部阻力系数的“阻力平方区”后，三通局部阻力系数基本趋于稳定。

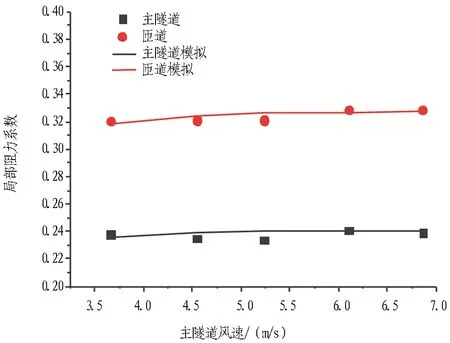
(a) 分流匝道

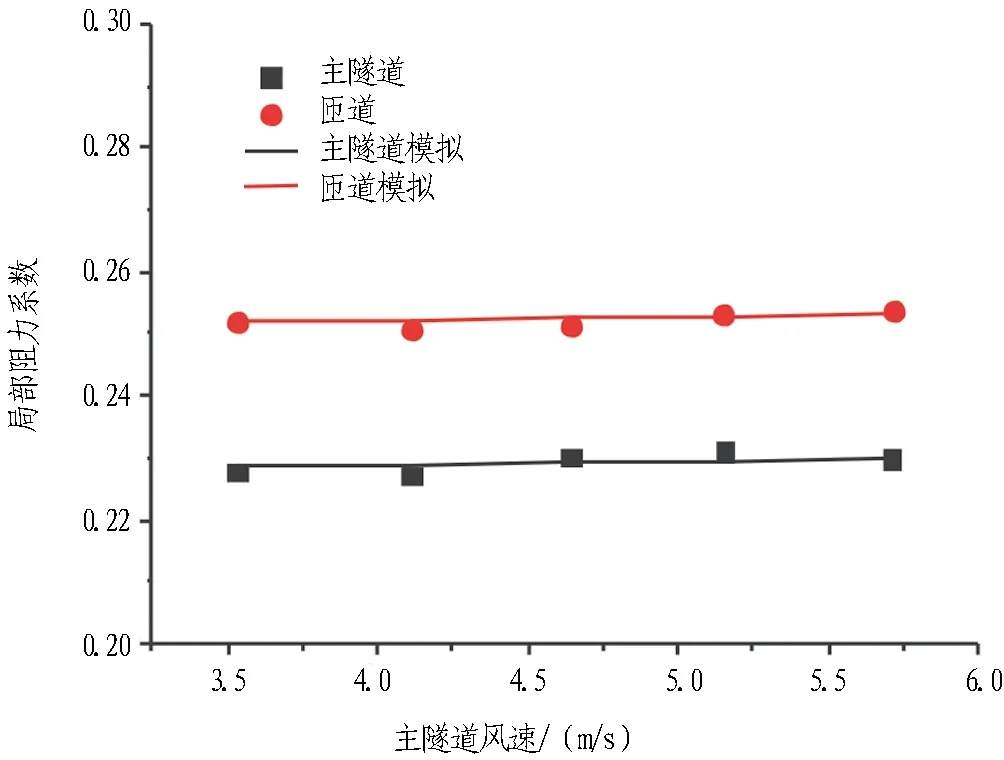
(b) 合流匝道

Fig. 7 Relationships between local resistance coefficient of confluence and distributary ramps and air speed

2.2 风量比的影响(工况2)

图9示出主隧道与匝道夹角为0°和30°时，风量比变化对分(合)流匝道局部阻力系数的影响规律。分流匝道情况下，主隧道和匝道的局部阻力系数都随风量比呈先下降后增大的趋势，其最小值分别出现在q1=0.6和q2=0.5左右，该规律不同于文献[13]关于矩形风管分流三通中直通管道局部阻力系数的变化规律； 合流匝道情况下，主隧道和匝道的局部阻力系数随风量比的增加呈单值增大的趋势，但q1和q2小于0.4时的主隧道、匝道的局部阻力系数均为负值，此规律与文献[13]关于矩形风管合流三通旁通管的趋势相同，但不同于直通管的变化规律。

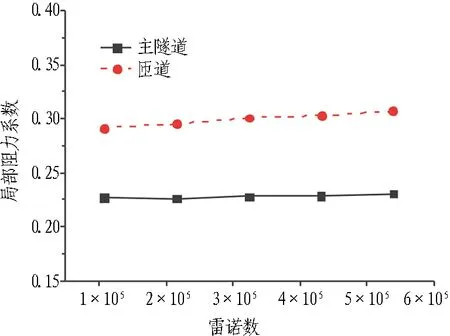
(a) 分流匝道

(b) 合流匝道

Fig. 8 Relationships between local resistance coefficient of confluence and distributary ramps andRe

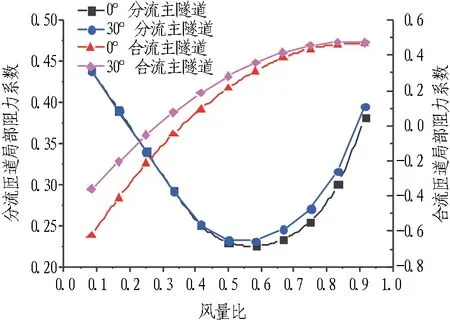
(a) 主隧道

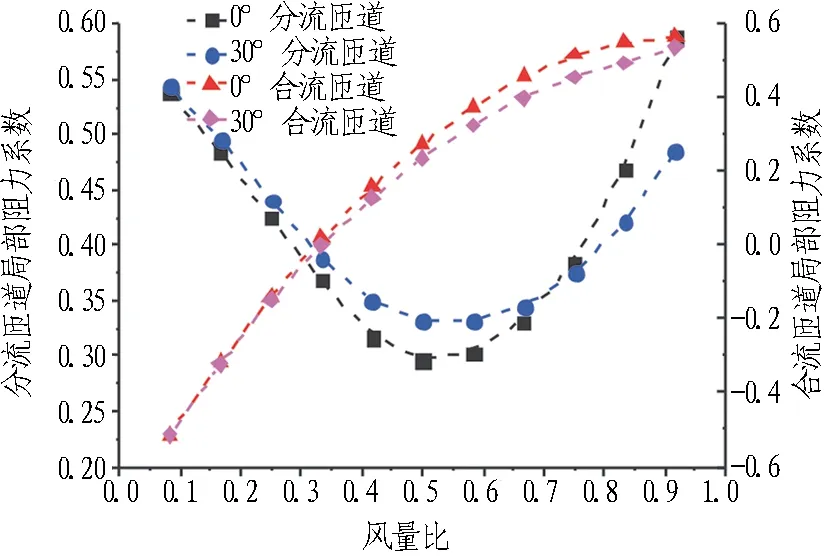
(b) 匝道

Fig. 9 Relationships between local resistance coefficient of confluence and distributary ramps andq

2.3 主隧道与匝道夹角的影响(工况3)

2.3.1 分流匝道

图10示出主隧道与匝道夹角分别为0°、10°、20°、30°时，分流匝道局部阻力系数的差异性。由图10(a)可知，当风量比小于0.5且风量比一定时，分岔角度变化对主隧道局部阻力的影响有限； 但当风量比大于0.5后，主隧道与匝道夹角变化对直隧道局部阻力系数的影响明显增大，特别是对匝道局部阻力系数的影响尤为显著。

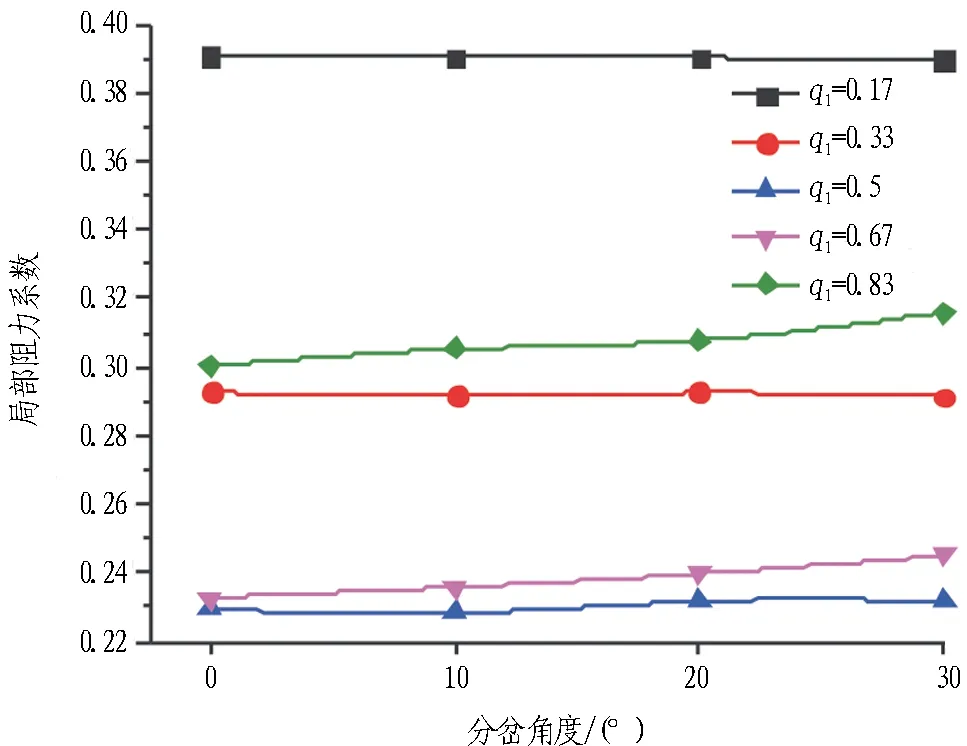
(a) 主隧道

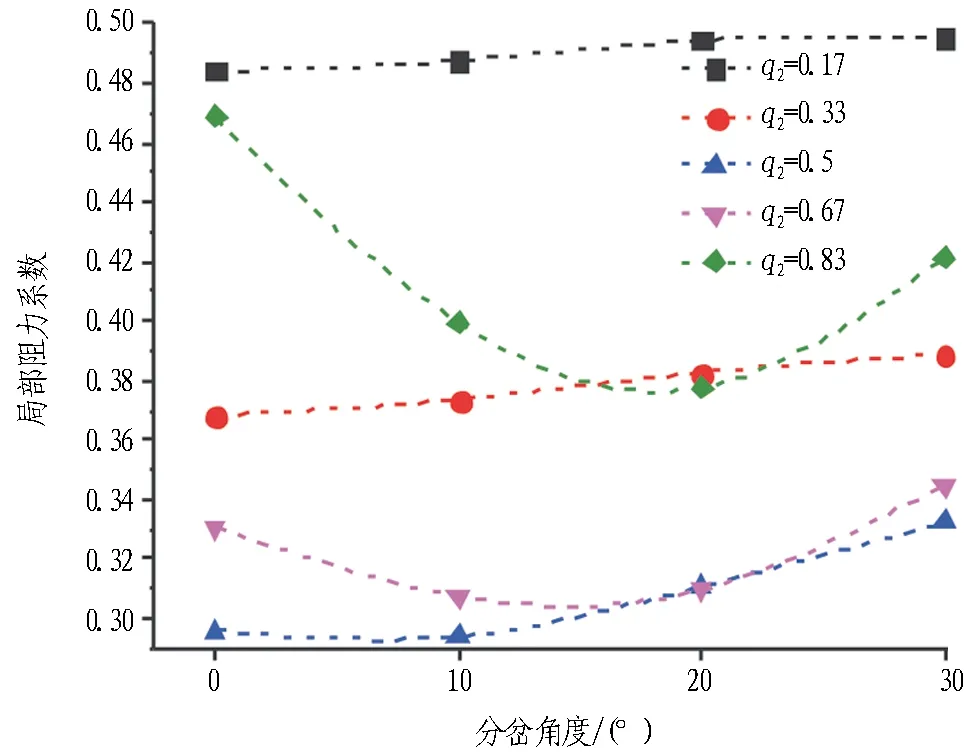
(b) 匝道

图10分流匝道局部阻力系数与分岔角度的关系

Fig. 10 Relationships between local resistance coefficient of distributary ramp andθ

图11为风量比q1=q2=0.5条件下的速度场计算云图。由图可知，随着主隧道与匝道夹角的增大，进入主隧道的流线分布基本没有发生变化，这意味着在q1=q2=0.5条件下，夹角变化对主隧道局部阻力系数的影响有限； 而随着夹角的增大，气流偏转角度增大，气流能快速充满整个隧道断面并均匀流动，匝道断面平均压力减小，局部阻力系数增大。

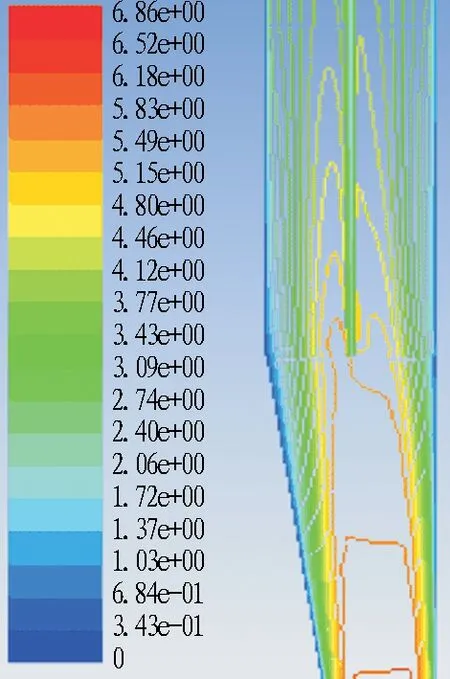
(a) 0°

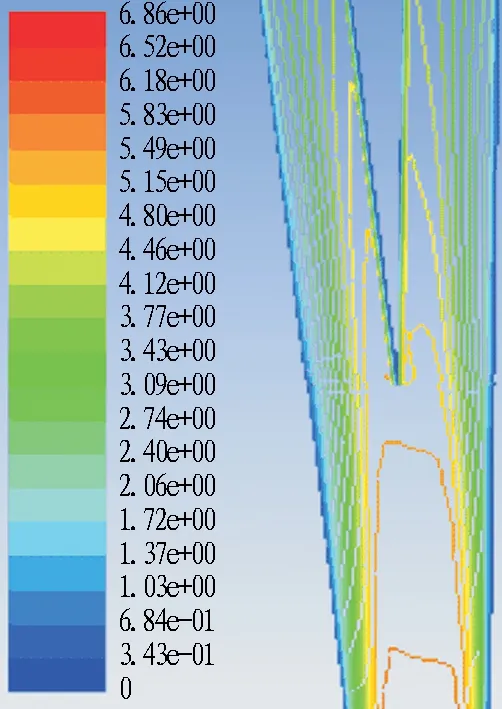
(b) 10°

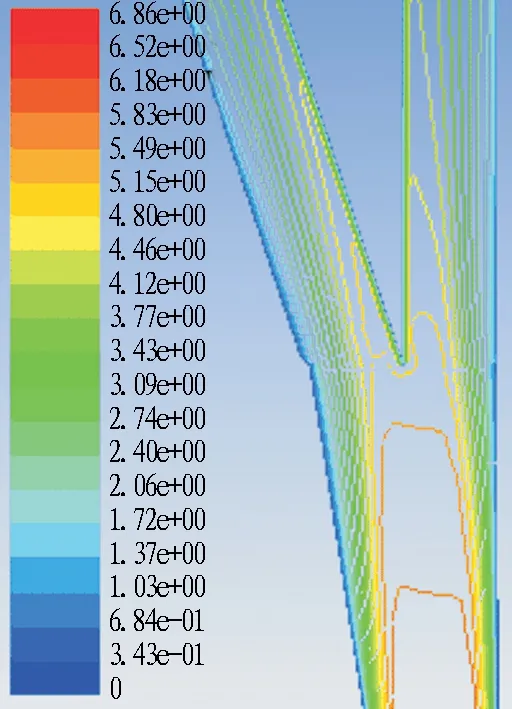
(c) 20°

(d) 30°

图11风量比q1=q2=0.5时分流匝道流速分布及流线图

Fig. 11 Flow velocity distribution and streamlines of distributary ramp whenq1=q2=0.5

2.3.2 合流匝道

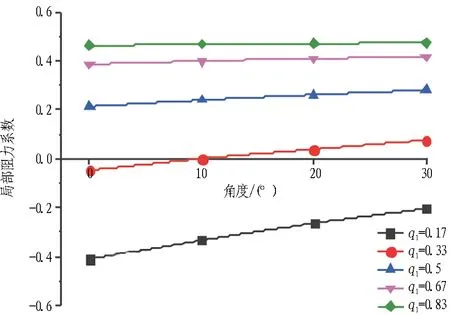
图12示出主隧道与匝道夹角分别为0°、10°、20°、30°时，合流匝道局部阻力系数的差异性。图12(a)示出随着主隧道与匝道夹角的增加，主隧道局部阻力系数呈单值上升趋势； 但随着风量比q1逐渐增大，这种影响在减弱。图12(b)反映了风量比的变化对匝道局部阻力系数的影响不可忽略，特别是风量比大于0.5后，这种影响更明显。

(a) 主隧道

(b) 匝道

图12合流匝道局部阻力系数与分岔角度的关系

Fig. 12 Relationships between local resistance coefficient of confluence ramp andθ

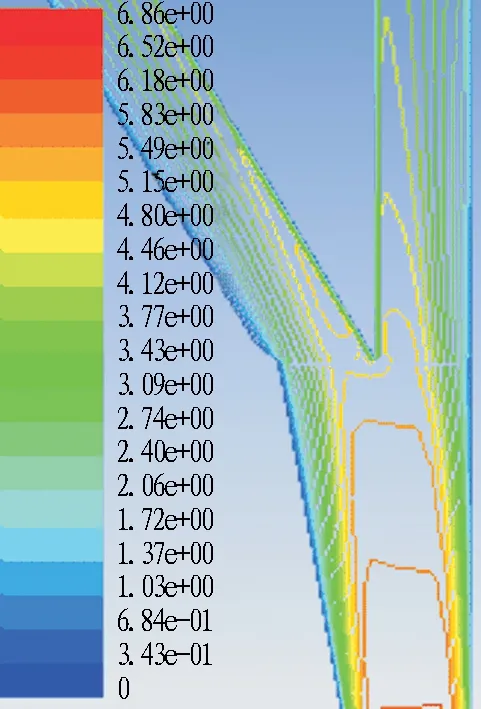
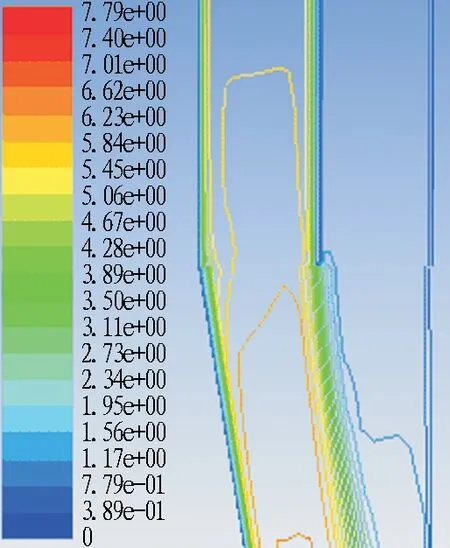
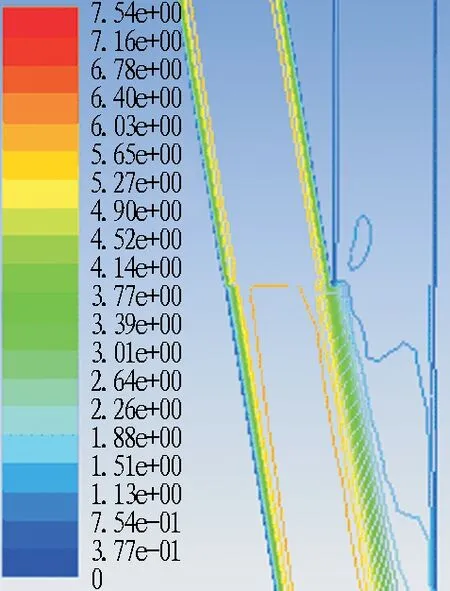
图13为风量比q1=0.17、q2=0.83时的流速分布及流线图。由图可知，随着主隧道与匝道夹角的增大，主隧道漩涡尺寸在逐渐增大，致使主隧道的局部损失增大。在匝道风量比q2=0.83的条件下，随着主隧道与匝道夹角的增大涡旋减弱，但是在30°夹角时涡旋又增多，这也是合流匝道局部阻力系数在0°、10°、20°、30°之间先减小后增大的原因。

2.4 局部阻力系数计算关联式

通过上述分析可知，风量比、主隧道与匝道夹角是影响分(合)流匝道局部阻力系数的关键因素。基于上述分析结果，根据最小二乘法并采用Matlab软件对计算结果进行多因素回归分析，可得到合流匝道主隧道局部阻力系数ξ13、匝道局部阻力系数ξ23关联式(3)—(4)； 分流匝道主隧道局部阻力系数ξ31、匝道局部阻力系数ξ32关联式(5)—(6)。

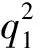
(3)

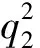
(4)

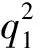
(5)

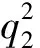
(6)

(a) 0°

(b) 10°

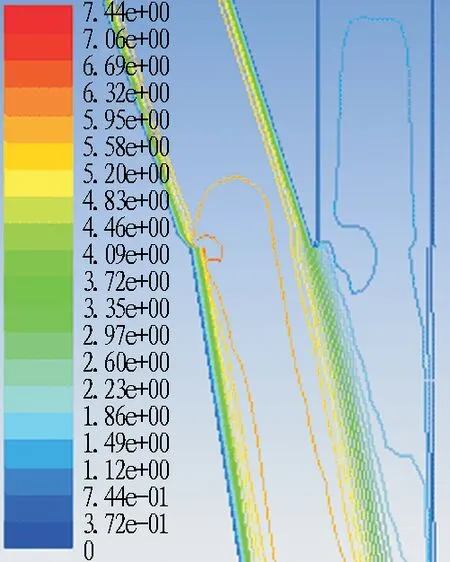
(c) 20°

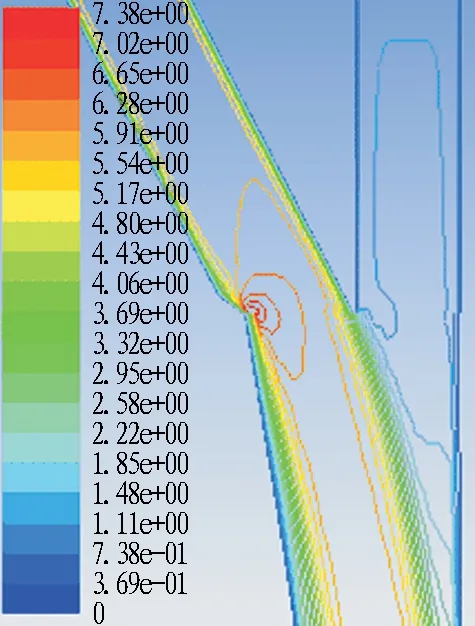
(d) 30°

图13风量比q1=0.17、q2=0.83时合流匝道流速分布及流线图

Fig. 13 Flow velocity distribution and streamlines of confluence ramp whenq1=0.17 andq2=0.83

3 结论与建议

基于长沙营盘路湘江隧道的实测、1∶8缩尺模型试验以及CFD数值分析结果，得到以下关于城市地下道路分(合)流匝道通风阻力特性研究结果：

1)主隧道与匝道风量比、主隧道与匝道夹角是影响分(合)流匝道局部阻力系数的关键因素。

2)城市地下道路分(合)流匝道局部阻力变化特性，尤其是分(合)流主隧道随风量比的变化规律完全不同于文献[13]，所以不宜简单套用通风管道的三通构件的参数。

3)基于长沙营盘路湘江隧道的计算结果，根据最小二乘法以及Matlab软件进行多因素回归分析，得出关于风量比和分岔角度的分(合)流匝道局部阻力系数计算关联式。

4)本研究结果基于长沙市营盘路湘江隧道的结构特征，即主隧道与匝道断面积基本相同。然而随着各种特长复杂城市隧道的修建，主隧道和匝道的结构特性也在发生变化，所以建议进一步研究分析多个断面积比条件下的分(合)流匝道局部阻力特性，为城市地下道路通风工程设计计算、相关标准与规范的制定提供方法参考。

[1] 李峰.公路隧道通风弯曲风道及火灾排烟风口优化研究[D]. 西安： 长安大学, 2009.

LI Feng. Study of the optimization of bending-duct in road tunnel and smoke outlets′layout in fire[D]. Xi′an: Chang′an University, 2009.

[2] 温玉辉.公路隧道排送通风系统升压模式分析研究[J].广东公路交通, 2011(4): 43.

WEN Yuhui. Study of pressure increasing principle of highway tunnel with exhaust and blow ventilation system [J]. Guangdong Highway Communications, 2011(4): 43.

[3] 喻映华, 雷波, 毕海权. 隧道紧急停车带流场和局部阻力数值模拟[J]. 现代隧道技术, 2006, 43(1): 49.

YU Yinghua, LEI Bo, BI Haiquan. Study of the airflow field and the coefficient of local resistance at the emergency parking place in a tunnel[J]. Modern Tunnelling Technology, 2006, 43(1): 49.

[4] 石平, 夏永旭. 公路隧道送排风短道流场数值分析及优化研究[J].地下空间与工程学报, 2009, 5(2): 402.

SHI Ping, XIA Yongxu. Numerical analysis and optimization research of short duct flow field of outlet and inlet in highway tunnel[J].Chinese Journal of Underground Space and Engineering, 2009, 5(2): 402.

[5] 马佳. 长大公路隧道通风系统局部结构优化研究[D]. 西安： 长安大学, 2015.

MA Jia. Study of the optimization of the long highway tunnel ventilation system on local structure[D]. Xi′an: Chang′an University, 2015.

[6] 苟红松, 吴元金, 李永生, 等. 隧道施工通风分风三通位置选择研究[J]. 隧道建设, 2016, 36(4): 384.

GOU Hongsong, WU Yuanjin, LI Yongsheng, et al. Selection of location of ventilation t-junction in tunnel construction[J]. Tunnel Construction, 2016, 36(4): 384.

[7] COSTA N P, MAIA R, PROENCA M F, et al. Edge effects on the flow characteristics in a 90 degree junction[J]. Journal of Fluids Engineering, 2006, 128: 1204.

[8] ABDULWAHHAB M, INJETI N K, DAKHI S F. Numerical prediction of pressure loss of fluid in a T-junction[J]. International Journal of Energy and Environment, 2013, 4(2): 253.

[9] 巩启涛, 杨俊红, 韩奎, 等. 大管径T型三通数值模拟及局部阻力特性分析[J]. 动力工程学报, 2016, 36(9): 753.

GONG Qitao, YANG Junhong, HAN Kui, et al. Characteristic analysis of the flow and local resistance in large pipe tees[J]. Journal of Chinese Society of Power Engineering, 2016, 36(9): 753.

[10] 石喜, 吕宏兴, 朱德兰, 等. PVC三通管水流阻力与流动特征分析[J]. 农业机械学报, 2013, 44(1): 73.

SHI Xi, LYU Hongxing, ZHU Delan, et al. Flow resistance and characteristics of PVC tee pipes[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(1): 73.

[11] 陈江林, 吕宏兴, 石喜, 等. T型三通管水力特性的数值模拟与试验研究[J]. 农业工程学报, 2012, 28(5): 73.

CHEN Jianglin, LYU Hongxing, SHI Xi, et al. Numerical simulation and experimental study of hydrodynamic characteristics of T-type pipes[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(5): 73.

[12] 陈伟业, 吕宏兴, 石喜, 等. 等径 PVC 三通管局部水头损失系数试验研究[J]. 灌溉排水学报, 2013, 32 (1): 128.

CHEN Weiye, LYU Hongxing, SHI Xi, et al. Experimental study of local loss parameter of diameter PVC pipe tee[J]. Journal of Irrigation and Drainage, 2013, 32 (1): 128.

[13] 陆耀庆. 实用供热空调设计手册[M]. 北京： 中国建筑工业出版社， 2008.

LU Yaoqing. Practical design handbook for heating and air conditioning[M]. Beijing: China Architecture & Building Press, 2008.

[14] 公路隧道通风设计细则: JTG/T D70/2-02—2014[S].北京： 人民交通出版社， 2014.

Guidelines for design of ventilation of highway tunnels: JTG/T D70/2-02—2014[S]. Beijing: China Communications Press, 2014.

[15] 方磊. 长大公路隧道通风物理模型试验研究[D]. 西安： 长安大学, 2005.

FANG Lei. The physical model experiment research of long highway tunnel ventilation[D]. Xi′an: Chang′an University, 2005.

VentilationResistanceCharacteristicsofConfluenceandDistributaryRampsofUrbanTunnel

YUAN Haoting1, CHEN Chao1, *, LI Qiong1, 2, WANG Luyao1, LI Yaru1

(1.CollegeofArchitectureandCivilEngineering,BeijingUniversityofTechnology,Beijing100124,China; 2.ArchitecturalEngineeringCollege,NorthChinaInstituteofScienceandTechnology,Beijing101601,China)

The ventilation resistance characteristics of confluence and distributary ramps of Xiangjiang River-crossing Tunnel on Yingpan Road in Changsha is studied by field monitoring, scale model experiment and software CFD numerical simulation; and then the influences of Reynolds number, air volume ratio and bifurcation angle on resistance characteristic of confluence and distributary ramps of the tunnel are analyzed so as to know the air flowing characteristics of urban underground passageway with bifurcated ramps. The results show that: 1) The air volume ratio and bifurcation angle are the key factors on the local resistance coefficients of confluence and distributary ramps. 2) The parameters of triplet joint component of ventilation pipe cannot be applied to characterize the variation of local resistance of confluence and distributary ramps. 3) The multiple-factor regression analysis of calculation results is carried out by least square method and software Matlab, which provides the expression equation of local resistance coefficient of confluence and distributary ramps of Xiangjiang River-crossing Tunnel on Yingpan Road in Changsha. The study results can provide reference for analysis of resistance characteristics of ventilation system and optimization of ventilation engineering design of urban underground passageway with complex structure.

urban bifurcate tunnel; confluence and distributary ramp; local resistance coefficient; scale model experiment; numerical simulation

2017-03-01;

2017-05-04

国家自然科学基金项目(51378024)； 北京市自然科学基金项目(8162006)

袁浩庭(1990—)，男，河北沧州人，北京工业大学暖通专业在读硕士，研究方向为隧道通风。E-mail： yhtbjut1990@163.com。*通信作者： 陈超， E-mail： chenchao@bjut.edu.cn。

10.3973/j.issn.2096-4498.2017.11.008

U 45

A

2096-4498(2017)11-1409-08