大跨度屋盖结构风振系数随厚度变化研究
2017-12-11郑群圣
郑群圣,朱 检
(1.永州市建设工程质量安全监督站,湖南 永州 425000;2.中建五局装饰幕墙有限公司,长沙 410000)
大跨度屋盖结构风振系数随厚度变化研究
郑群圣1,朱 检2
(1.永州市建设工程质量安全监督站,湖南 永州 425000;2.中建五局装饰幕墙有限公司,长沙 410000)
为研究大跨度薄壳屋盖结构屋盖厚度与风振系数关系问题,首先建立了时域内大跨度薄壳屋盖结构空间三维风振分析模型.然后通过FORTRAN软件平台编制基于谐波叠加法的脉动风载荷程序.最后采用ANSYS瞬态动力计算得到屋盖结构的风振系数值,并分析出该类屋盖结构的风振系数与屋盖厚度之间的变化趋势.结果表明,谐波叠加法是模拟风荷载的有效方法,大跨度屋盖结构的位移风振系数值随厚度的减小而增大,其中跨中部位为受风荷载影响最为显著.数值算例验证了本文方法的正确性与有效性,为屋盖结构的抗风设计提供理论依据和工程参考意义.
谐波叠加法;有限元方法;厚度变化;穹顶结构;风振系数
大跨度空间结构广泛应用于国民建筑中.随着建筑技术水平的提升,以及新型材料的迅猛发展,使得屋盖自重愈发轻巧、跨度大幅增加,但存在柔性较大、阻尼小、自振频率较低等特征,从而风载属于各类大跨度屋盖结构必须考虑的控制荷载之一[1-2].
相比高层建筑而言,大跨度屋盖结构实用抗风设计理论及方法仍处于探讨阶段.在大跨度屋盖设计初期,少有工程师意识到风荷载的激励作用对结构影响之大,并常认为风产生的吸力有利于屋面结构.但基于种种大跨度屋盖结构因风损毁的事故表明:风在屋盖上产生的吸力,还有脉动风荷载于结构上所造成的振动,会对屋面造成巨大破坏.
目前,随着屋盖厚度越来越轻薄化发展趋势,大跨度屋盖结构在风荷载作用下被破坏几率增大[3-4].因此,对大跨度屋盖结构进行风振响应研究越来越重要,有必要考虑各种结构细节因素(屋盖厚度等)对大跨度屋盖结构风致响应的影响进行细致研究.
本文利用有限元商业通用软件ANSYS对大跨度薄壳屋盖结构在时域内进行三维风振分析,通过FORTRAN平台编制基于谐波叠加法的脉动风载荷程序,通过脉动风压功率谱和Wiener-Khintchine定理,获取脉动风速时程样本的风压时程利用ANSYS中的瞬态动力分析计算大跨度薄壳屋盖结构的风振系数值,并通过风振系数值确定大跨度屋盖结构的最不利荷载部位.同时考虑了不同厚度影响下,风振系数的变化趋势,得出该类屋盖结构的风振系数随厚度变化的变化规律.为大跨度空间结构的抗风设计提供理论依据.
1 风振效应分析方法
本文主要介绍时域法在ANSYS中的具体实现方法.其实现一般步骤为:
(1)基于风速时程模拟理论,编制相应的程序模拟出风速时程,这个过程一般在 MATLAB或FORTRAN编程实现;
(2)风速样本时程通过脉动风压功率谱和 定理转化为风压样本时程;
(3)根据屋面结构的有限元离散化,将节点风压时程施加于屋面结构;
(4)利用ANSYS中瞬态动力分析对屋盖结构进行时程分析,得到结构风振响应与风振系数.
2 风荷载模拟
2.1 风荷载基本特性
在工程实际应用中,通常将风荷载作为静力风(或称平均风)与动力风(或称脉动风)的共同作用[4].平均风可作为静力或恒载考虑,而脉动风要用随机振动理论来处理,因此风的模拟主要是针对脉动风而言[5-6].
聘请行业相关高层管理人员、专家担任兼职导师,邀请他们为学生讲授行业动态,企业需求等,开阔学生视野。比如邀请有留学经历的行业精英为学生讲解留学规划、细分行业领域和工作性质,职业晋升路线等具体资讯,帮助学生了解行业信息,做好个体职业生涯规划。
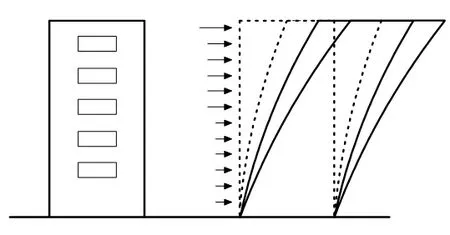
图1 平均风脉动风共同作用下建筑物
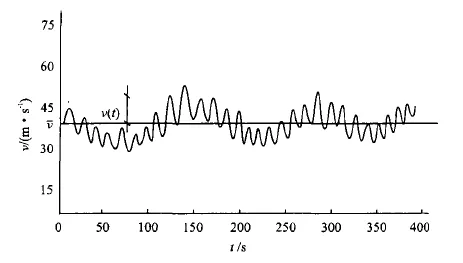
图2 平均风脉动风示意图
2.2 风荷载模拟
真实的脉动风场为多维多变量的零均值平稳高斯随机过程[7],但在计算机模拟过程中通常将其简化为一维n变量零均值平稳高斯随机过程,其双边互谱密度矩阵为[6]
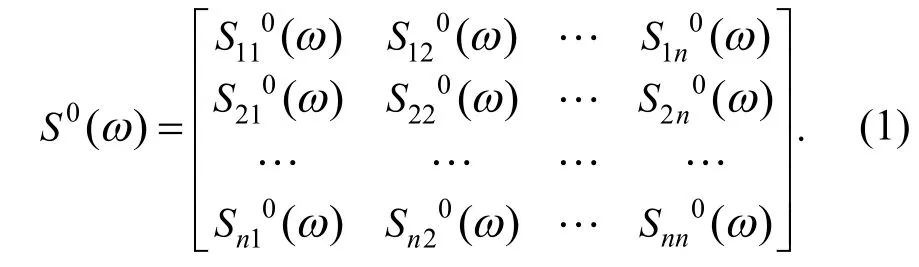
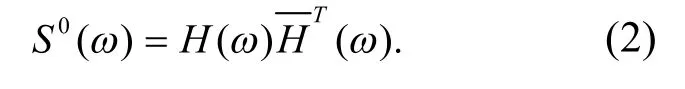
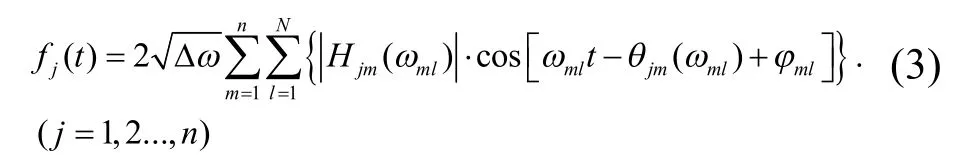
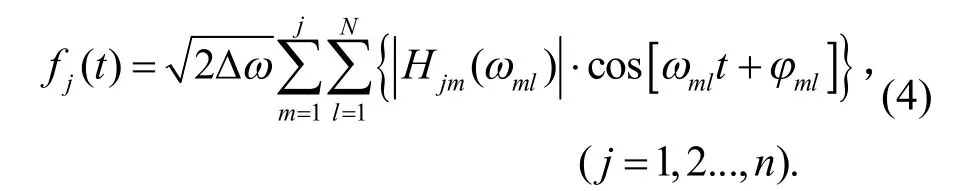
式中,N为上下频率范围之间总共频率段数.通过快速傅里叶变换技术,通常取为 2的整数次幂.jml为均匀分布于(0,2p)区间的独立相位角.Shinozuka引入了双索引频率来增大模拟样本周期,为
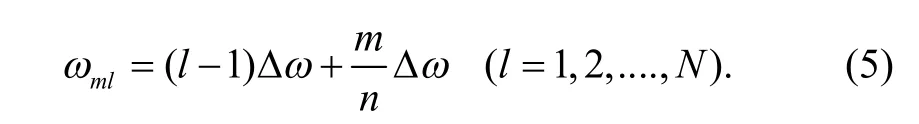
式(4)为一系列简谐波的叠加,每个谐波分量的周期为
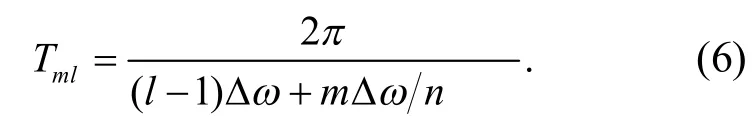
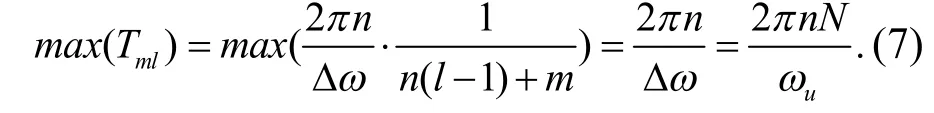
将式(4)整理为
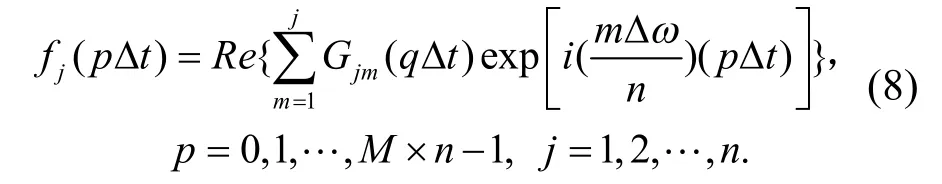
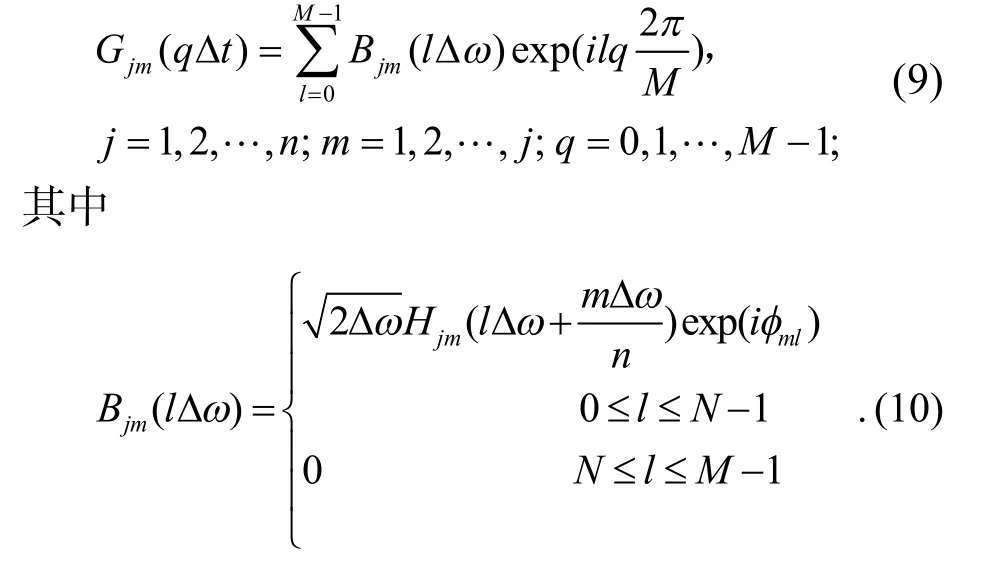
2.3 风速谱与功率谱
由于大跨度屋盖结构横向、纵向、竖向跨度非常大,故模拟该类结构的脉动风,需考虑采用水平和竖直风速谱共同作用[7].其中水平方向与竖直方向脉动风速谱分别采用 Davenport谱与Panofsky谱,其表达式为
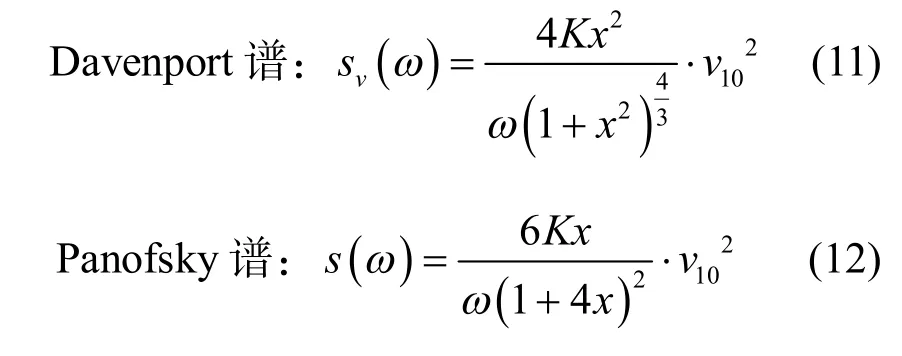
空间2点间的互功率谱密度由自谱密度函数与2点的空间相关系数共同决定.可以表示为
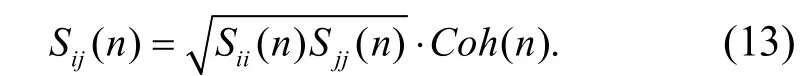

2.4 风速与风压转换关系
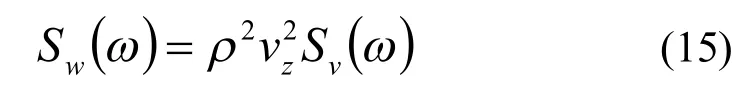
3 算例分析
在计算中,选择大连天座建筑艺术工程有限公司的工程实例:跨度D=40 m、半径R=20 m的薄壳屋盖(带加劲肋48个),加劲肋规格2d´40d=7.8´156 (mm2),整个薄壳穹顶结构支撑在高为h=60 m的刚性支座上.其中ANSYS模型中壳体部分采用薄壳单元,加劲肋部分采用梁单元.壳体与加劲肋的密度分别为弹性模量均为E=215 GPa,泊松比均为.模型计算简图和约束情况如图3-图4所示;在计算中对几种不同尺寸的结构进行了计算分析,厚度取为可变参数如表1所示.
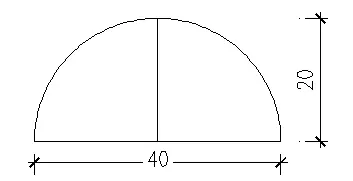
图3 模型计算简图/m
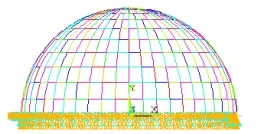
图4 有限元模型底边约束图
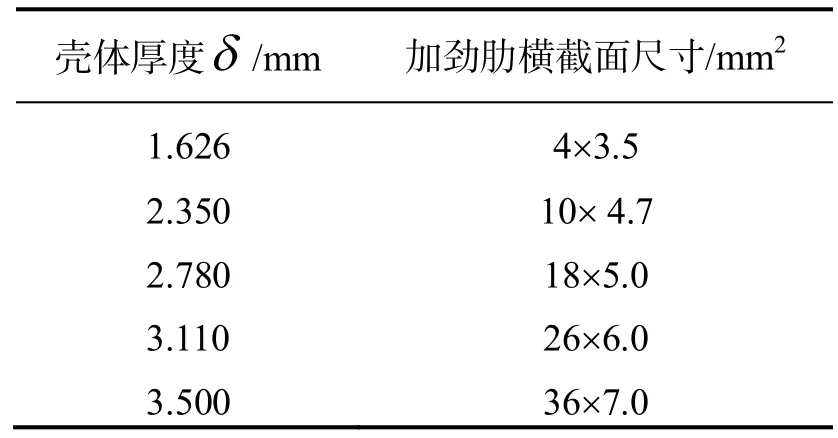
表1 厚度与横截面尺寸表
3.1 风场模拟算例
根据工程算例中研究对象所处地理位置,应用FORTRAN软件平台编程模拟大连地区60 m高度处的风荷载.基本风速基本风压按大连地区选取.C类地面粗糙度,地面粗糙系数规范中,取地面粗糙度指数大气密度频率取样点数风速模拟时间为时间步长为0.2 s.图5(a)和(b)分别为屋盖跨中点水平与竖直脉动风速时程曲线.
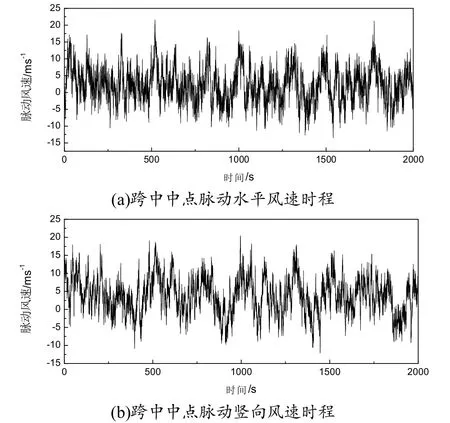
图5 屋盖结构模拟的脉动风速时程
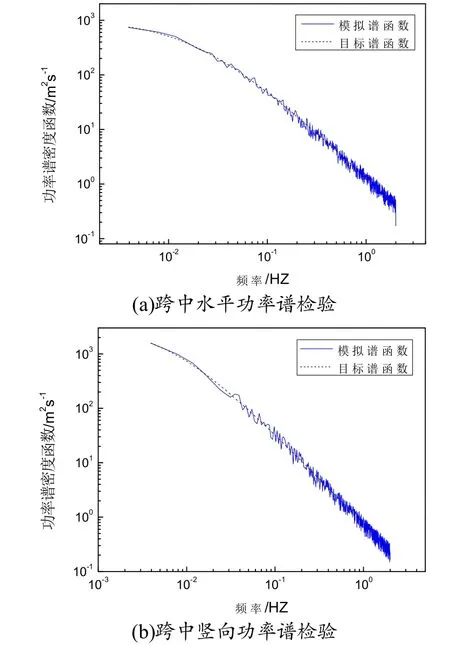
图6 功率谱密度函数检验
图6和图7分别为屋盖跨中中点功率谱密度函数检验和相关性检验.由图可得风速时程吻合良好,所得样本的精度满足工程计算.
3.2 结果分析
本文风荷载考虑平均风荷载与脉动风荷载,通过将平均风荷载和脉动风荷载工作用施加到五种不同厚度工况下屋盖结构屋面节点,选取通过薄壳体中心顶点的一组径向节点进行风振系数计算,风振系数公式为[7]
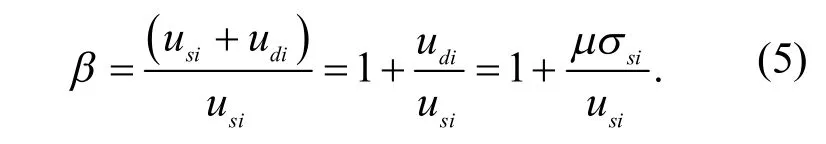
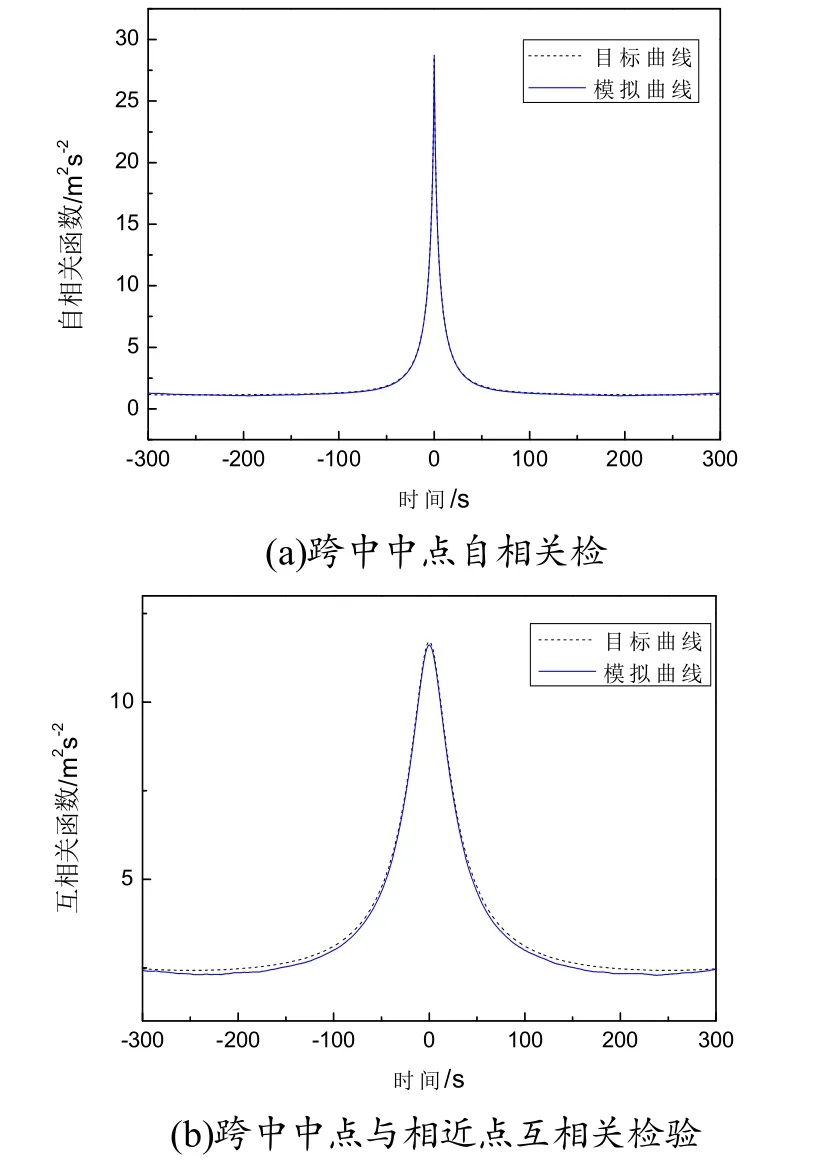
图7 相关性检验
本文中结构阻尼采用瑞利阻尼,经 ANSYS进行瞬态分析,计算得到所选取的径向节点的位移值以及位移响应均方根值,将其分别代入式(5),得到风振系数值和风振系数平均值分别如图8和图9所示.
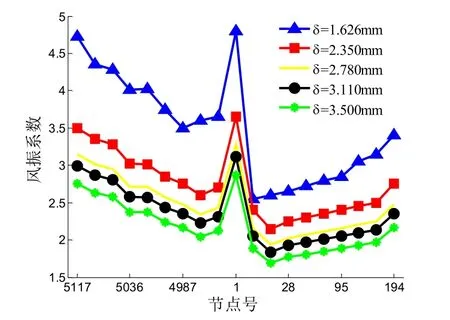
图8 不同节点在不同厚度时风振系数值
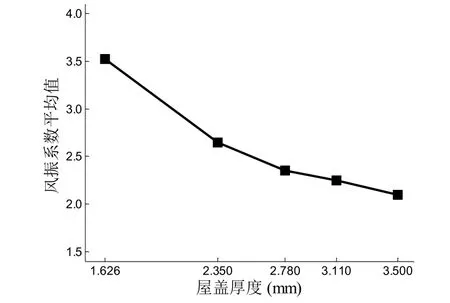
图9 不同厚度风振系数平均值
从图9中可以看出,屋盖结构受其厚度影响最为显著.针对同样分析模型,当跨度相同,矢高相同,矢跨比相同时,随着屋盖厚度的增加,其结构的位移风振系数呈现逐渐减小的变化规律,即厚度的增加有利于结构的抗风.而风振系数在跨中部位出现了突变,同样说明了跨中部位为薄弱部位,在结构抗风设计时应着重考虑此部位,且明确结构中的最不利位置及荷载.
4 结论
(1)本文推导了模拟脉动风场的谐波叠加法,通过COMPAQ VISUAL FORTRAN软件平台编制了风场模拟程序,并通过数值算例验证了基于谐波叠加法模拟所得风速时程样本的精度满足工程计算需要.
(2)当屋盖结构在跨度为40 m,矢高为20 m时,其跨中部位受风荷载影响最为明显,针对该类屋盖结构设计时应着重考虑此部位最不利荷载.
(3)当跨度、矢高一定时,该类屋盖结构风振系数呈现随其屋盖厚度减小而增大的变化趋势,即厚度的增加对结构的抗风是有利的.但是结构厚度的增加必将增加结构自身的重量,反而对结构自身的强度和结构的抗震能力有不利的影响,因此,针对该类大跨度屋盖结构的设计时,需要考虑风荷载的效应,且需要综合考虑各种因素之间的相互的影响.
[1]任德斌, 魏欢, 贾洪涛, 等. 玻璃纤维增强水泥复合板的力学性能[J]. 沈阳建筑大学学报, 2008, 24(6): 1005-1008.
[2]任德斌, 李楠, 杨丽丽, 等. 钢拱壳穹顶结构在集中荷载作用下随厚度变化应力趋势预测[J]. 沈阳建筑大学学报, 2010,26(2): 286-291.
[3]黄本才. 结构抗风原理及应用[M]. 上海: 同济大学出版社,2001: 1-10.
[4]张相庭. 结构风工程[M]. 北京: 中国建筑工业出版社, 2006.
[5]陆锋, 楼文娟, 孙炳楠. 大跨度平屋面的风振响应及风振系数[J]. 工程力学, 2002, 19(2): 52-57.
[6]闫石, 郑伟. 简谐波叠加法模拟风谱[J]. 沈阳建筑大学学报,2005, 21(1): 1-4.
[7]罗俊杰, 韩大建. 大跨度结构随机脉动风场的快速模拟方法[J]. 工程力学, 2008, 25(3): 1-6.
(责任编校:徐赞)
Analysis of the Span Roof Structures Wind Vibration Coefficient with Different Thickness
ZHENG Qun-sheng1, ZHU Jian2
(1. Yongzhou City Construction Engineering Quality and Safety Supervision Station, Yongzhou, Hunan 425000, China;2. China Construction Five Board Decorative Curtain Wall Limited Liability Company, Changsha, Hunan 410000, China)
By using harmonic superposition method combined with FORTRAN program, we simulated wind load, got fluctuating wind speed curve and fluctuating wind pressure curve, used the finite element method combined with ANSYS, conducted three dimensional wind vibration analysis in time domain on a span roof structure, obtained its wind vibration coefficient and determined its most unfavorable part of wind induced vibration. At the same time, taking the wind vibration coefficient variation trend into account at different thickness, we got the variation with thickness changes. The results show that harmonic superposition method is an effective way to simulate fluctuating wind in time analysis. Span roof structures wind coefficient increases with the thickness decrease, whose central part is the most unfavorable part of wind induced vibration. Therefore, this paper provides a reference for the dome structure in wind resistant design and an analysis method for large span structures wind resistant design.
harmonic superposition; finite element method; thickness; large span roof structure; wind vibration coefficient
O334.1
A
10.3969/j.issn.1672-7304.2017.02.0005
1672–7304(2017)02–0020–05
2016-08-18
郑群圣(1982-),男,湖南永州人,硕士研究生,主要从事建设工程质量安全监督与管理研究,E-mail: zhengfei240@163.com.
