基于测风数据的经验尾流模型适用性分析研究

吴阳阳

（华能国际电力股份有限公司浙江清洁能源分公司，杭州 310014）

基于测风数据的经验尾流模型适用性分析研究

吴阳阳

（华能国际电力股份有限公司浙江清洁能源分公司，杭州 310014）

风电机组的尾流效应是风电场能量损失的重要因素，研究尾流效应是为了优化风机布置，尽量减小风力机尾流的影响，降低风电场能量损失，使风电场的经济性达到最佳。而现有的许多工程应用的经验尾流模型，在准确性和适用性上都存在差异。以单台水平轴风电机组经验尾流模型为研究对象，分析了Jensen模型、Larsen模型、Frandsen模型和无粘近场模型等具有代表性的经验尾流模型的各自优缺点以及适用条件。然后，针对Jensen模型和无粘近场尾流模型的缺点进行了改进，并结合改进Jensen模型与改进的无粘近场尾流模型，分段建立了准确度更高适用性更强的全场尾流模型。最后，基于Sexbierum风电场尾流区测风数据对建立的全场尾流模型进行了对比验证。结果表明，全场尾流模型能够较好的拟合风场的实测数据，可以适用于风力机全场尾流速度分布的模拟以及指导工程实践。

风电机组；尾流模型；对比验证；全场尾流模型

0 引言

风力机是将自然界风能转化为机械能进而转化为电能的核心设备。当风吹过风力机时引起风轮的旋转，由于风动能到风轮机械能的转换，风力机下游会出现风速减小、湍流强度增大、风剪切加剧等流动特征；经过一段下游距离之后，在周围气流的作用下风速逐渐得到恢复，这被称为风力机的尾流效应。风速的降低使得下游风力机的输出功率降低，强湍流和附加的风剪切会影响下游风力机的疲劳载荷、结构性能和使用寿命，进而影响整个风电场的运营寿命。

风电场中许多风力机布置在一起，一些风力机将处于另一些风力机的尾流中，使风力机的性能受到影响，功率输出减小，影响整个风电场总的功率输出[1]。开展尾流效应对风力机性能影响研究是为了合理布置风力机，尽量减小风力机尾流的影响，提高风电场效率，使风电场的经济性达到最佳。

尾流模型是描述风力机尾流结构的数学模型，用于计算风力机尾流区的速度分布和风电场中处在尾流区的风力机的功率输出。

目前使用的尾流模型有基于实验总结的半经验的尾流模型、基于涡流理论的模型和基于N-S方程的CFD模型。涡流理论模型与CFD模型虽然计算精度较高，但是其对计算资源的要求是非常高的，庞大的计算量及漫长的计算时间是实际工程应用不能接受的。这使得半经验尾流模型得到非常广泛的应用，半经验尾流模型具有计算精度较高、结构与计算相对简单的优势，从而在被微观选址和功率预测软件如WAsP和WindPRO等商业软件所采用。1986年，丹麦国家工程实验室的N.O.Jensen基于风轮一维动量理论提出了Jensen[2]模型，该模型主要适用于平坦地形且被作为WAsP软件的尾流模型基础。陈坤等在Abramovich射流理论的基础上提出了AV尾流模型[3]，该模型是一种全场尾流模型。此外，还有著名的无粘近场尾流模型、简化尾流模型、Larsen[4]尾流模型。

在风电场微观选址、风电场短期功率预测等工程应用中，通常采用经验尾流模型来定量描述尾流效应的影响。而现有的许多工程应用的经验尾流模型，在准确性和适用性上都存在差异。

1 尾流模型介绍

1.1 Jensen模型

Jensen模型是最经典的一维尾流模型之一，它是由N.O.Jensen于1986年提出的。该尾流模型结构简单，假设尾流场横截面上风速均匀分布，风速径向分布廓线呈帽子形状。且尾流场半径是线性扩张的，尾流场横截面的初始直径为风轮直径。图1为Jensen模型示意图。类似地，以下介绍的Larsen与Frandsen模型示意图横、纵轴意义均与Jensen模型示意图相同。

尾流场速度分布规律：

式中：s=x/D；D为风轮直径；u为沿轴向距风轮x处的速度；U∞为风轮前的来流风速；CT为风轮推力系数；k为尾流场半径增长率，当上游风速为自然风时，k取0.04，否则，k取0.08。

图1 Jensen模型示意

尾流场直径与尾流场速度分布都取决于风轮下游的位置。

1.2 Larsen模型

Larsen模型是由G.C.Larsen提出来的，它是基于普朗特紊流边界层方程的解析表达式，并且假定尾流区域的风速衰减具有相似性。它运用了普朗特的混合长度理论，进一步认为流动是不可压缩的，忽略风剪切的影响，因此尾流是轴对称的。图2为Larsen模型示意图。

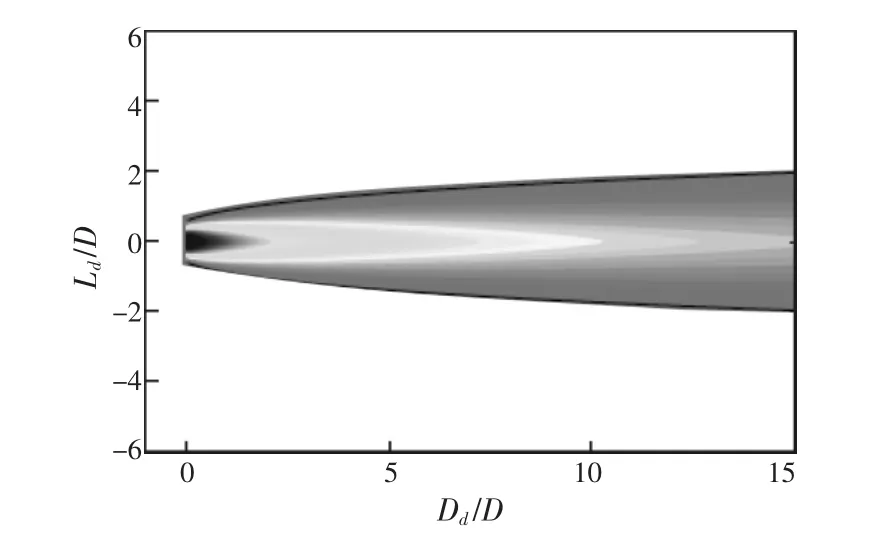
图2 Larsen模型示意

风轮下游x处尾流区风速衰减：

式中：c1普朗特混合长度，是无量纲数值；CT为风轮推力系数；A为风轮扫掠面积；U∞为风轮前的来流风速；x0为风轮位置。

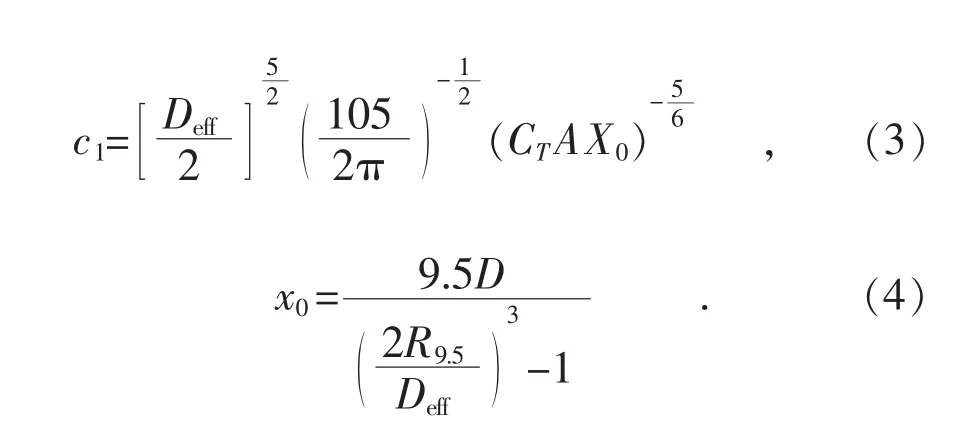
有效风轮直径Deff：

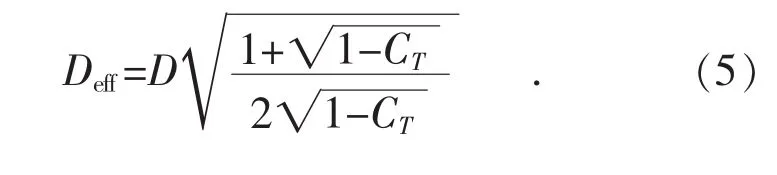
下游距离风轮9.5倍风轮直径处的尾流区域半径R9.5：

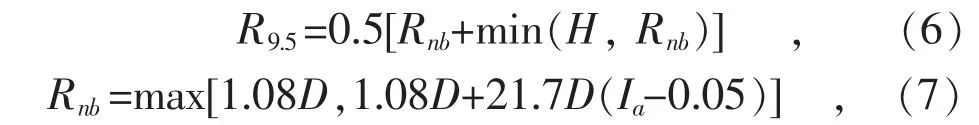
式中：H为风力机轮毂高度；Ia为环境湍流强度。

风力机的尾流效应使得下游机组承受更高的湍流载荷，Larsen尾流模型可以分析尾流对下游湍流水平的影响，更适用于风电功率预测[7]。

1.3 Fransen模型

比Jensen和Larsen模型提出更晚的一个方法是Storpark分析模型（SAM），这种模型是在2006年欧洲风能大会介绍和展览的，由学者Frandsen提出的。SAM的目的是预测大型海上风电场恒定行距的矩形网格的速度衰减规律。图3为Fransen模型示意图。

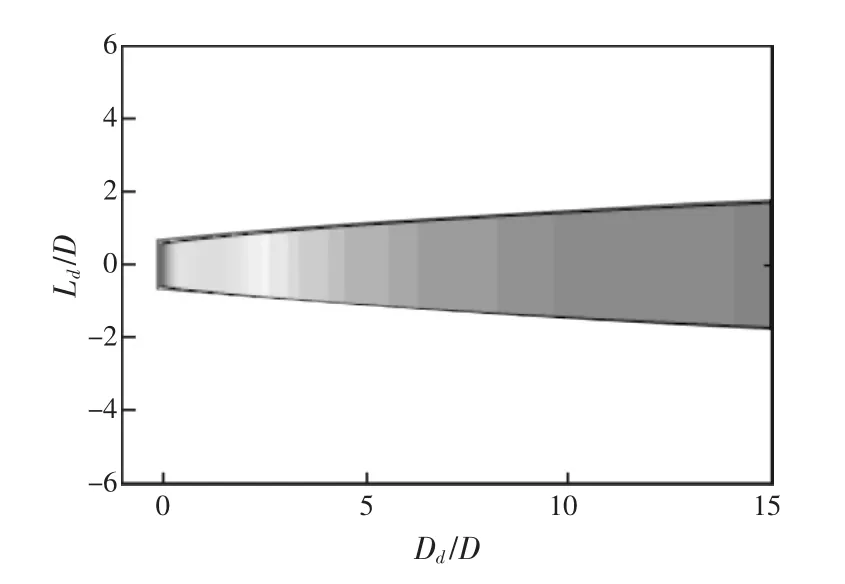
图3 Fransen模型示意

尾流场速度分布规律：

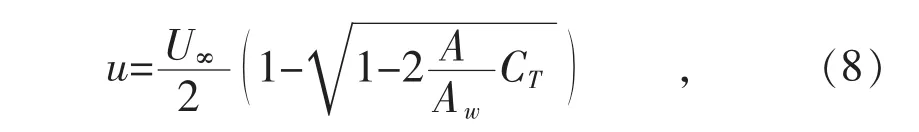
式中：CT为风轮轴功率系数；u为距风轮x处的速度；U∞为风轮前的来流风速；A为风轮扫掠面积；Aw为风轮下游x处的横截面积。

1.4 无粘近场模型

无粘近场尾流模型是适用于描述近场尾流（x≤5D）的速度分布规律的模型，对于近场尾流区可以采用无粘近场模型。

假定风电机组近场尾流区的空气流动是无粘旋转的流动，且尾流区横截面的速度分布是均匀的，根据毕奥-萨伐尔定理可得风力机尾流区域速度分布[5]：

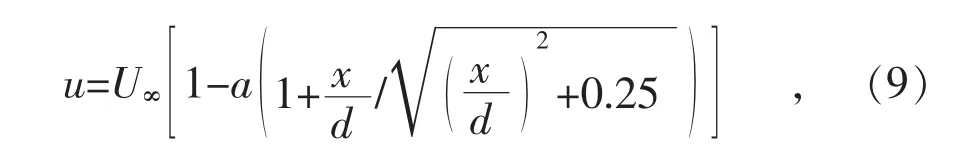
式中：u为距风轮x处的速度；U∞为风轮前的来流风速；a为轴向诱导因子；d为风轮直径。

2 基于风洞试验测风数据的尾流模型适用性分析

依据第一节介绍的尾流模型，应用MATLAB软件编写对应的计算程序，得到各尾流模型的速度衰减规律，并将各自的计算结果绘制成图表与风洞实验数据对比，总结规律，分析了各尾流模型的的优缺点及适用性。

2.1 TNO风洞与风力机模型介绍

TNO是荷兰国家应用科学研究院（Netherlands Organisation for Applied Science Research）的英文缩写，致力于工程技术的研究和应用，是荷兰主要的航天航空研究机构。实验是在阿珀尔多伦大气边界层TNO风洞中进行的，风洞是一个开放型埃菲尔直流式风洞。该风洞实验的详细参数如表1所示。

表1 风洞试验段与风电机组模型参数

2.2 基于风洞试验测风数据的各尾流模型对比及适用性分析

基于风洞试验参数，应用MATLAB软件编写对应的计算程序，得到各尾流模型的速度衰减规律，并将各自的计算结果绘制成图表与风洞试验测风数据对比。

计算结果与实验数据对比见图4—9。

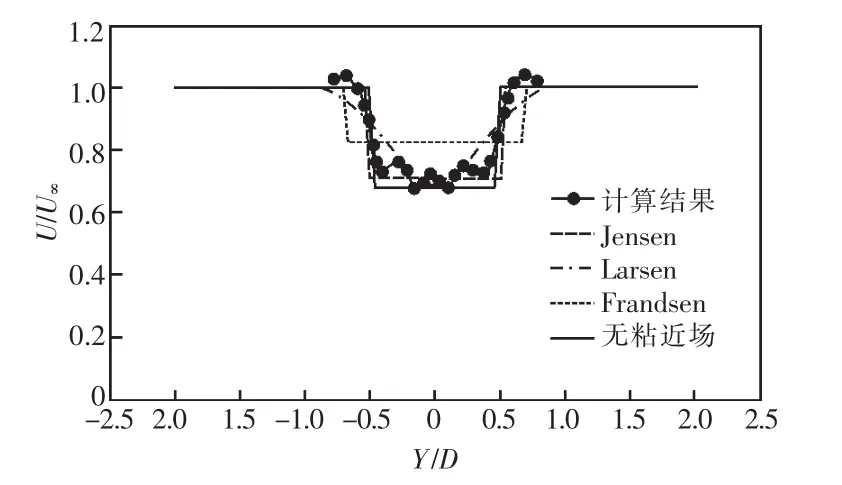
图4 CT=0.56，x=D

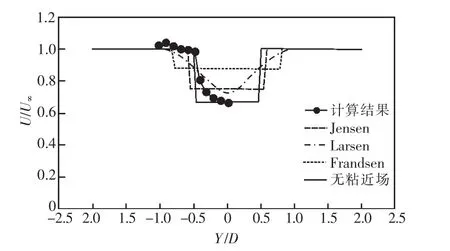
图5 CT=0.56，x=2D

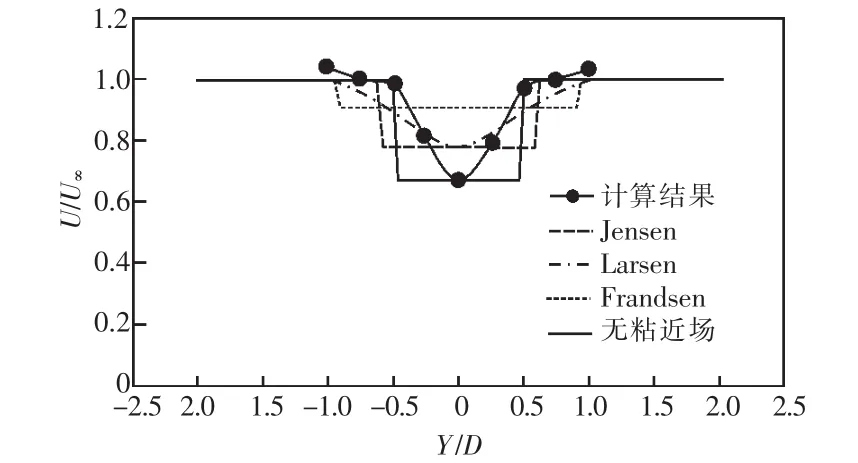
图6 CT=0.56，x=3D

图7 CT=0.56，x=5D

图8 CT=0.56， x=8D

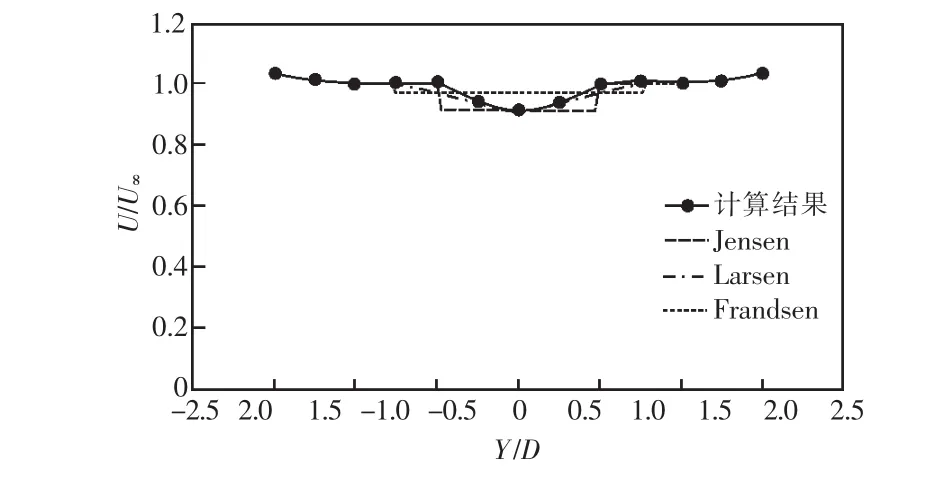
图9 CT=0.56，x=12D

图4—9中，Y为尾流区域中某点距风轮水平轴的垂直距离，横坐标值为Y与风轮直径D的比值，纵坐标值为尾流场中某点风速u与风轮前来流风速u∞的比值。

从图4—9得到以下结论：

（1）图4中，由于受到轮毂对尾流区域的影响，在x=1D时，尾流中心区的实测数据呈波浪形，其他位置呈抛物形分布。

（2）Jensen 尾流模型在近场（1D≤x≤3D）低估了尾流中心区速度衰减的最大值，而在远场（x＞3D）比较接近尾流中心区的衰减得最大值。

（3）无粘近场尾流模型在近场（1D≤x≤3D）十分接近尾流中心区速度衰减的最大值，对其进行正弦修正之后就能较准确的反映尾流区的速度变化规律。

（4）Larsen 尾流模型在近场（1D≤x≤3D）普遍低估了尾流中心区的速度衰减值，而在远场（x＞3D）与实际的测风数据曲线很接近。

（5）Frandsen尾流模型在近场和远场普遍低估了尾流区的速度衰减值，但远场误差比近场小。

2.3 初步建立全场尾流模型

依据基于风洞试验测风数据的尾流模型的优缺点对比及适用性分析，初步建立了全场尾流模型A与B。

模型A：近场1D≤x≤3D，改进的无粘近场尾流模型；远场x＞3D，Larsen尾流模型。

模型B：近场1D≤x≤3D，改进的无粘近场尾流模型；远场x＞3D，改进的Jensen尾流模型。

3 尾流模型的改进

3.1 Jensen模型的修正

Jensen模型假设尾流场横向剖面的速度分布是均匀的。从实际情况以及大量的实验结果来看（TNO风洞实验结果也可以看出），在实际的尾流场中，尾流场径向的速度分布应该是抛物线型的。这与三角函数的图像非常相似，所以对Jensen模型进行正弦修正，使修正后的模型径向速度分布呈抛物线型，修正后的模型示意如图10所示。

图10 修正后的Jensen模型

由式（1）可知，尾流区速度衰减量：

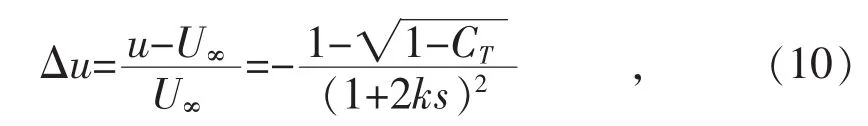
式中：Δu为速度衰减量，是无量纲数值。

令y方向为垂直方向，修正后的速度分布规律符合标准的正弦关系：

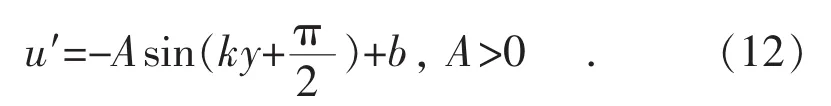
根据正弦函数的特征求出A，k，b，得到修正后模型的速度分布规律为：

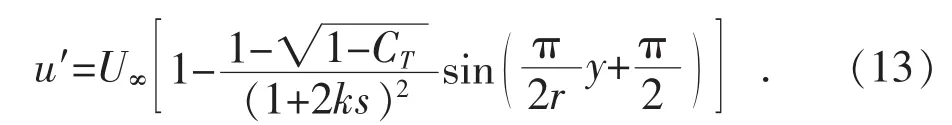
3.2 无粘近场模型的修正

类似于Jensen尾流模型，无粘近场模型也是假设尾流区剖面的速度分布是均匀的。运用类似于Jensen模型的修正方法对无粘近场模型进行正弦修正，得到修正后的无粘近场模型速度分布规律：

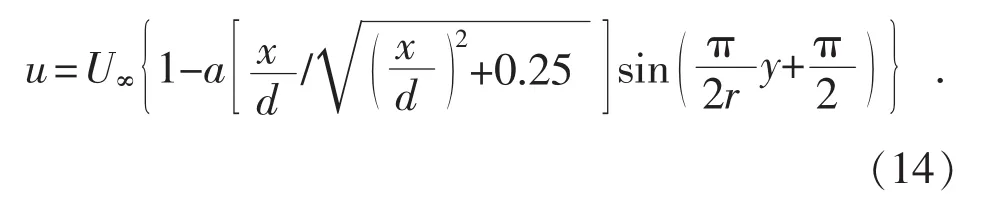
式中：a为风力机轴向诱导因子；d为风轮直径；y为尾流区某点到水平轴的径向距离。

4 全场尾流模型的确立

改进的Jensen尾流模型比Larsen尾流模型准确度高，能较准确的反映实测数据情况，故在远场采用改进的Jensen尾流模型，全场尾流模型采用模型B。

当1D≤x≤3D，改进的无粘近场尾流模型：

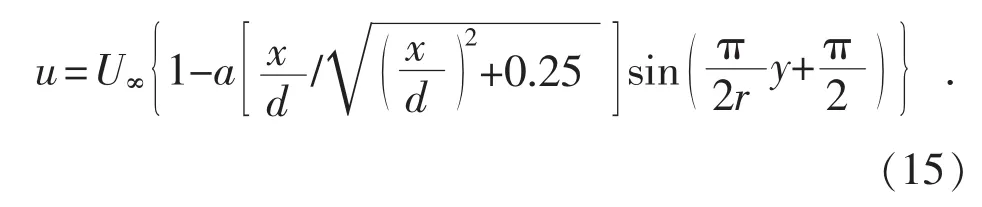
当x＞3D，改进的Jensen尾流模型：

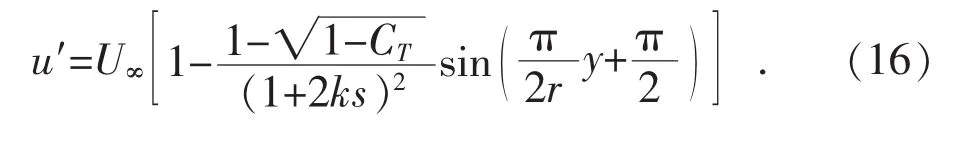
5 全场尾流模型验证算例

5.1 Sexbierum风场简介

Sexbierum风场是位于荷兰北部的平坦地形的陆上风电场，距离海岸大约4 km。风电场总装机5.4 MW，拥有18台额定功率为310 kW的机组。风电机组风轮直径30 m，轮毂高度30 m，切入风速、额定风速、切出风速分别为5 m/s，14 m/s， 20 m/s。

5.2 全场尾流模型的验证

选取Sexbierum风场的测风数据作为全场尾流模型的验证算例，模型计算参数为：风轮直径、轮毂高度、风轮轴推力系数。应用MATLAB软件分段编写程序，计算得到全场尾流区速度分布。

将计算结果与实际测风数据进行对比，结果如图11—13所示和如表2—4所示。

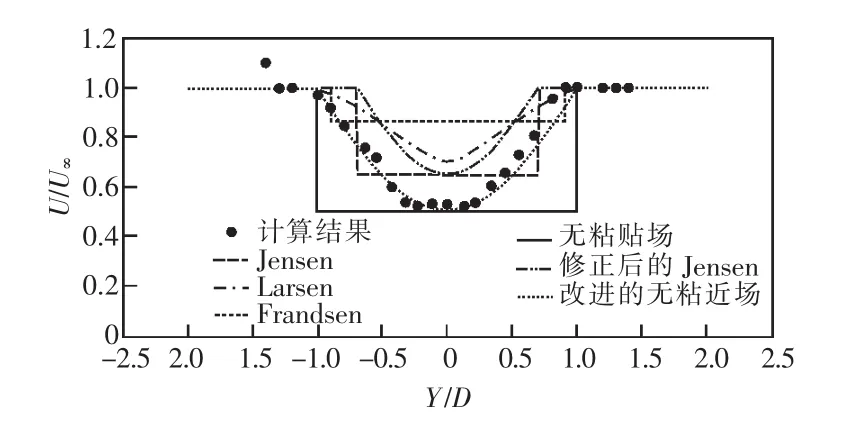
图11 CT=0.75，x=2.5D

图12 CT=0.75，x=5.5D

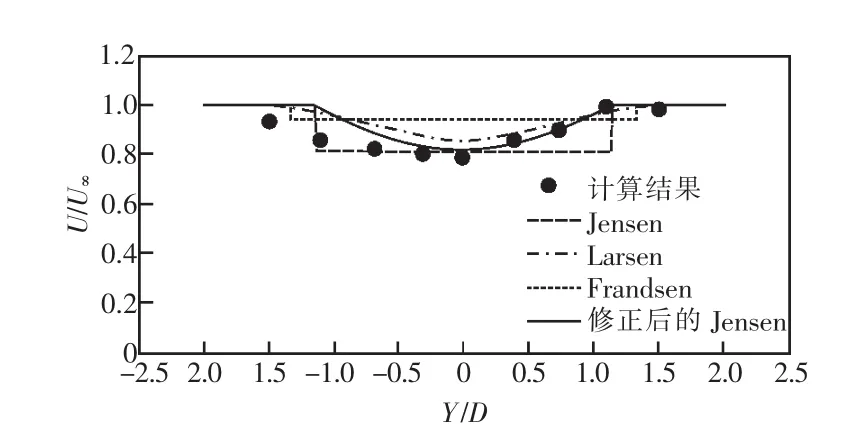
图13 CT=0.75，x=8D

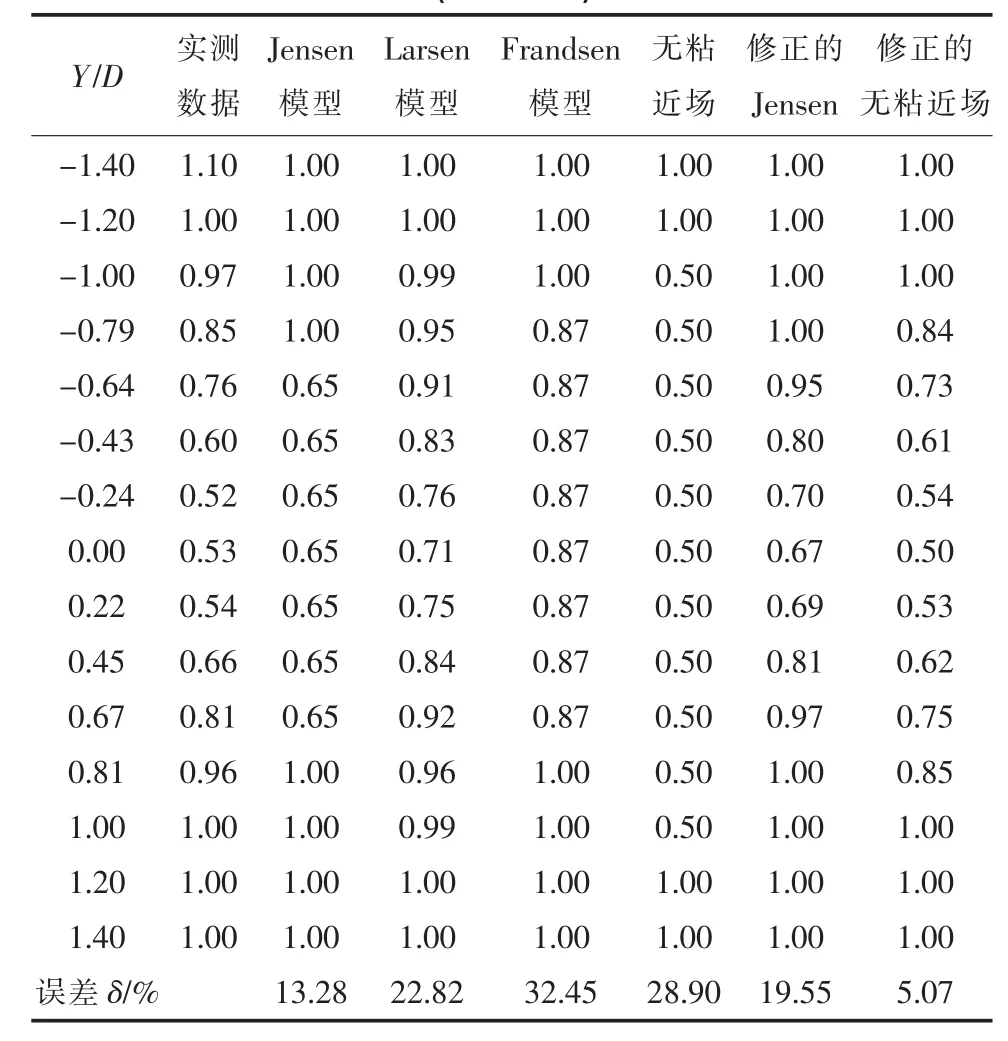
表2 测风数据与对应各模型的U/U∞计算结果（x=2.5D）

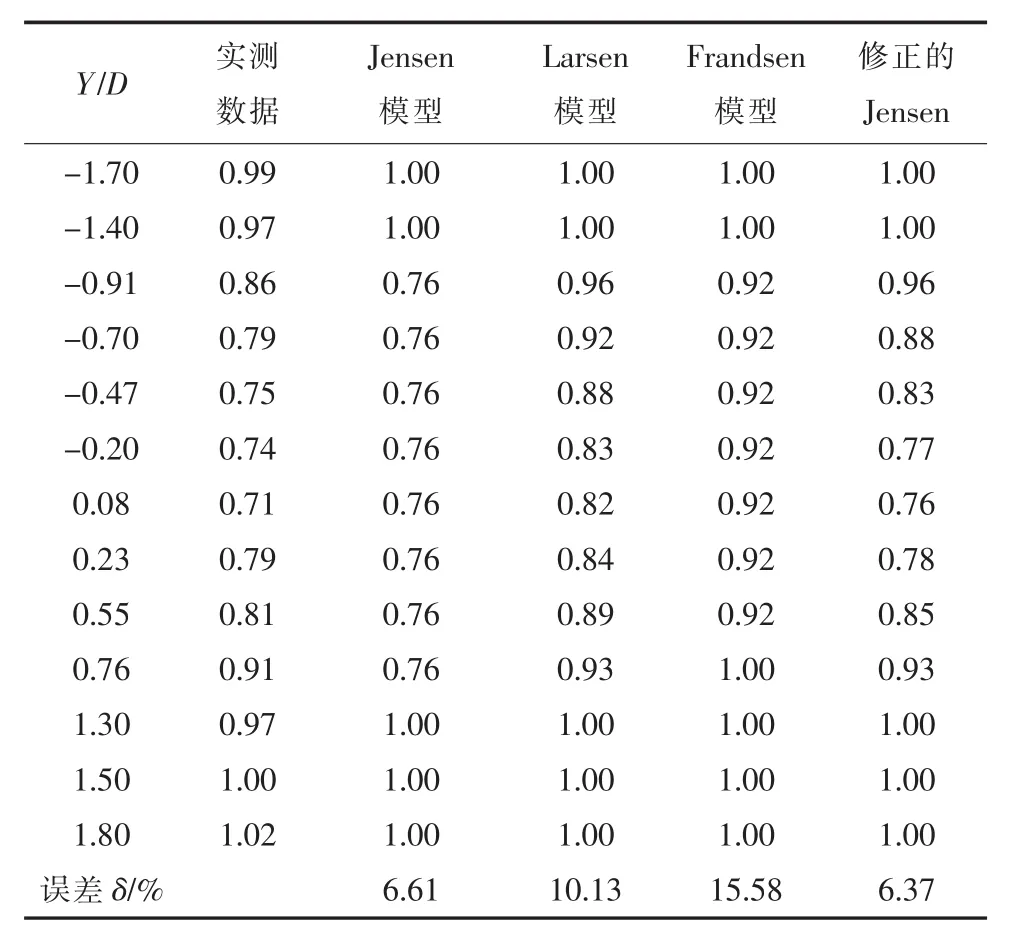
表3 测风数据与对应各模型的U/U∞计算结果（x=5.5D）

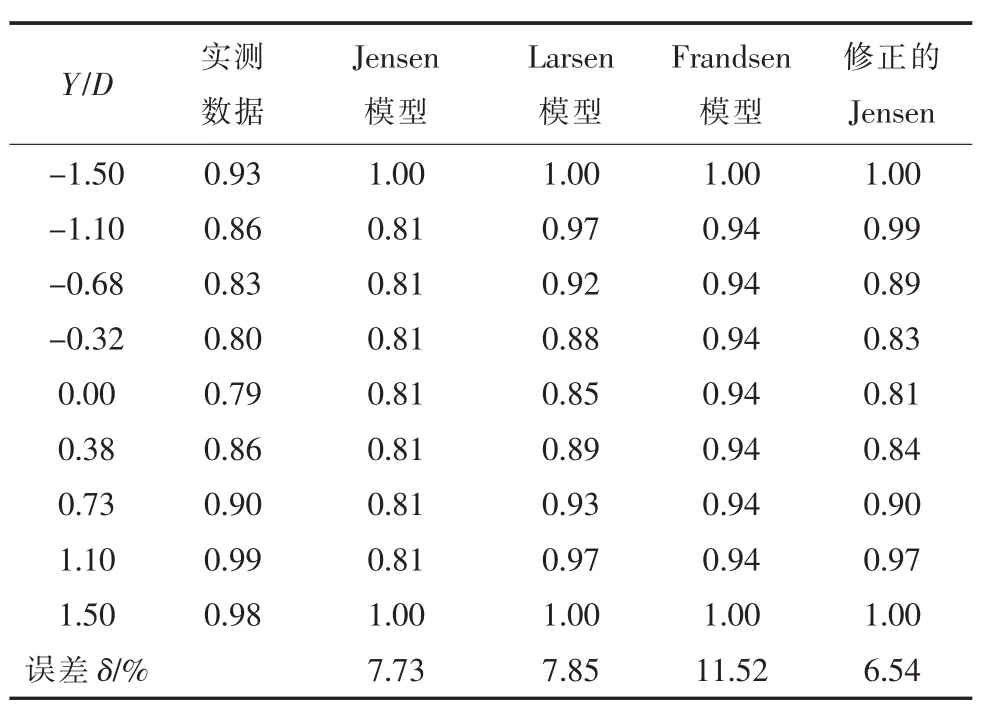
表4 测风数据与对应各模型的U/U∞计算结果（x=8D）

误差计算验证：

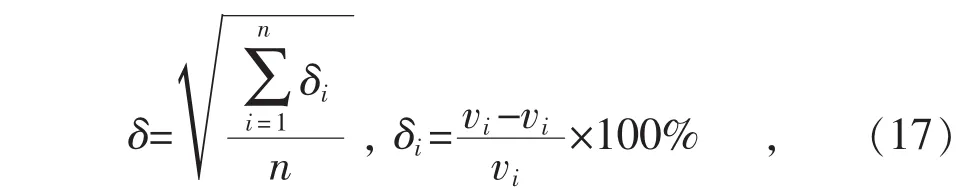
式中：δi为尾流区第i个测量点处的相对误差；vi为尾流区第i个测量点处的模型计算风速；vi为尾流区第i个测量点处的实际风速。

依据表2—4可以看出，x=2.5D时，修正的无粘近场模型与实测数据的误差最小，且与实测数据十分接近；x=5.5D时，修正的Jensen模型的误差最小，与实测数据最接近；x=8D时，修正的Jensen模型的误差较其他模型最小，与实际测风数据最接近。这与建立的全场尾流模型吻合，验证了全场尾流模型的适用性，可以应用到实际的工程指导中。

6 结论

基于风洞数据进行了尾流模型适用性分析，对比几种常见的经验尾流模型，得到以下结论：

（1）Jensen尾流模型能较准确计算出远尾流区最大风速衰减值。但风速沿径向均匀分布的假设与试验和风电场测量数据不符。大量的实验结果和数值模拟表明，在实际的尾流场中，尾流场径向的速度分布应该是近似抛物线型的。

（2）Larsen尾流模型描述了尾流区风速径向的变化，且风速预测精度在远场较高。

（3）Frandsen尾流模型预测陆地风场尾流的速度普遍要比实际尾流区的风速高，它低估了尾流区的速度衰减量。

（4）无粘近场尾流模型能够较准确地计算出近尾流区最大风速衰减值，但也未描述风速沿径向的变化。

针对无粘近场尾流模型与Jensen尾流模型的缺点进行了改进，得到风速沿径向变化的改进模型。根据各尾流模型在机组后不同距离处的适用性，分段选取适用的模型组建了全场尾流模型，并基于风电场实地测风数据进行了验证，结果表明，全场尾流模型尾流区风速计算精度更高。

[1]陈树勇，戴慧珠，白晓民，等.尾流效应对风电场输出功率的影响[J].中国电力，1998，31（11）∶28-31.

[2]JENSEN N O.A note on wind generator interaction[R].Riso-M-2411，Riso National Laboratory，1983.

[3]Wind turbine wake models developed at the technical university of Denmark[C]//Renewable and Sustainable Energy Reviews，2015.

[4]LARSEN G C，MADSEN H A，SORENSEN N N.Mean wake deficiting the near field[C]//European Wind Energy Conference and exhibition，Madrid，Spain，2003.

[5]陈坤，贺德馨.风力机尾流数学模型及尾流对风力机性能的影响研究[J].流体力学实验与测量，2003，17（1）∶84-87.

[6]SANGHYEON JEON，BUMSUK KIM，JONGCHUL HUH.Comparison and verification of wake models in an onshore wind farm considering single wake condition of the 2 MW wind turbine[G].2015.

[7]陈晓明.风场与风力机尾流模型研究[D].兰州：兰州理工大学，2010.

[8]张镇，张晓东.风电场中风力机尾流模型研究[D].吉林：华北电力大学，2012.

[9]唐田.大型风电场风电机组尾流模型及其应用研究[D].吉林：华北电力大学，2015.

[10]曾利华，王丰，刘德有.风电场风机尾流及其迭加模型的研究[J].中国电机工程学报，2011，31（19）∶37-42.

[11]Wind turbine wake models developed at the technical university of Denmark[C]//Renewable and Sustainable Energy Reviews，2015.

[12]张永，韩春雷，范海兵.计及风机集群效应的风电场等值模型研究[J].浙江电力，2014，33（3）∶10-13.

[13]李仁年，司小冬.一种水平轴风力机尾流模型及其计算方法[J].兰州理工大学报，2012，38（1）∶37-40.

[14]杨祥生，赵宁，田琳琳.一种二维尾流数值模拟方法[G].2015.

[15]胡丹梅，欧阳华，杜朝辉.水平轴风力机尾迹流场试验[J].太阳能学报，2006，27（6）∶7-13.

[16]陆莹，罗辇.一种确定发电厂风机风量标定系数的新思路[J].浙江电力，2012，31（10）∶59-61.

2017-09-22

吴阳阳（1993），男，从事清洁能源发电行业研究工作。

（本文编辑：陆 莹）

下期要目

●电网负载健康评估模型研究

●面向高维数据的凹型自表示特征选择方法

●基于分段非线性函数的无功补偿经济性模型研究

●分时电价下考虑舒适度的家庭负荷调节特性分析

●基于数据包络法对配电网投入产出效益的评价

●海量日志分析在浙江电力的应用与实践

●面向丽水电网负荷“峰谷倒置”特性的电价策略研究

●基于多源数据挖掘的低压配电网线损异常的智能诊断模型

●基于曲线相似度和关联分析的窃电智能识别与预警

●基于图像技术的电网运行态势分析及其应用

奉献清洁能源 建设和谐社会

Applicability Analysis of Empirical Wake Model Based on Wind Data

WU Yangyang
（Huaneng Power International.， Inc.， Zhejiang Clean Energy Branch， Hangzhou 310014， China）

The wake effect of wind turbine is an important factor of energy loss in wind farm.The wake effect is studied in order to better the fan arrangement， minimize the influence of the wind tail flow， reduce the energy loss of the wind farm， and optimize the economic efficiency of the wind farm.However， the existing empirical wake models of many engineering applications are different in accuracy and applicability.Based on an empirical wake model of a single horizontal axis wind turbine as research object，this paper analyzes the advantages and disadvantages of representative models such as Jensen model，Larsen model，Frandsen model and inviscid near field model and the applicable conditions； then， according to the disadvantages Jensen model and the inviscid near field wake model are improved；based on the improved Jensen model and the improved the inviscid near field wake model，a whole-field wake model with higher accuracy and applicability is established by sections.Finally，based on the Sexbierum wind farm wake data the whole field wake model is compared and validated.The result shows that the model can well fit the measured data of wind field and can be applied to whole field wake velocity distribution simulation of wind turbines and engineering practice guidance.

wind turbine；wake model；comparison and verification；whole field wake model

10.19585/j.zjdl.201711017

1007-1881（2017）11-0092-06

TM621.2；TK223.26

A