仿生策略优化的鲸鱼算法研究*

巩世兵， 沈海斌

(浙江大学 超大规模集成电路设计研究所，浙江 杭州 310027)

仿生策略优化的鲸鱼算法研究*

巩世兵， 沈海斌

(浙江大学超大规模集成电路设计研究所，浙江杭州310027)

通过对混沌映射初始化种群和自适应调整搜索策略对鲸鱼优化算法(WOA)改进，提出了仿生策略优化的鲸鱼算法(BWOA)，实现了对算法的全局优化能力和收敛速度的改进。通过基准测试函数的仿真，BWOA与标准WOA及高效的WOA(EWOA)对比分析，证明了BWOA的有效性。

鲸鱼算法； 仿生策略； 群智优化算法； 切比雪夫序列； 混沌映射初始化种群

0 引 言

启发式优化算法具有简单易实现、能有效避免局部最优、可扩展性好等优点，广泛应用于各种工程设计中[1]。启发式算法的思想来源于各种生物机制、物理规律，一般可以分为两类：基于个体的方法[2]和基于群体的方法[3]。其中基于群体的方法有：遗传算法(genetic algorithm,GA)、粒子群优化(particle swarm optimization,PSO)算法[3]、蚁群优化(ant colony optimization,ACO)算法[4]、蜂群算法(bee colony algorithm,ABC)[5]、细菌觅食优化算法(bacterial foraging optimization algorithm,BFOA)[6]、萤火虫算法(firefly algorithm,FA)[7]、布谷鸟算法(cuckoo algorithm,CS)[8]、果蝇优化算法(fruitflies optimization algorithm,FOA)[9]、鲸鱼优化算法(whale optimization algorithm,WOA)[1]等。事实上，这些算法均没有对参数空间的数据完全利用，得到的结果也具有一定随机性[2]。为了实现对数据的充分利用和快速收敛的目标，新的算法在研究中不断被提出。

本文提出了仿生策略优化的鲸鱼优化算法(biomimetic whale optimization algorithm,BWOA)以混沌映射初始化种群和自适应调整搜索策略的方式实现对基本鲸鱼算法的仿生策略优化，避免局部收敛，提高收敛速度。

1 标准鲸鱼算法

WOA算法[1]模仿座头鲸的捕食机制，在优化过程中以50 %的概率随机选择收缩圈方式和螺旋气泡网方式更新个体的位置。

1.1 收缩圈方式

鲸鱼算法假设当前的最佳候选方案是目标位置或是接近目标的位置。在最佳搜索代理被定义后，其他搜索代理将试着朝向最佳搜索代理更新其位置。该行为表示为

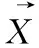
(1)

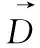
(2)

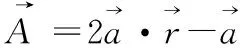
(3)

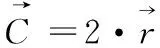
(4)

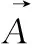
1.2 螺旋气泡网方式

在鲸鱼位置和猎物位置之间使用螺旋方程模拟座头鲸的螺旋状移动

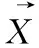
(5)

(6)

式中b为定义对数螺线形状的常数；l为[-1,1]的随机数。

1.3 搜索阶段

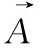
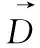
(7)

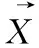
(8)

2 BWOA

BWOA在鲸鱼算法的基础上，利用混沌映射初始化种群和自适应调整搜索策略实现鲸鱼算法的仿生策略优化。

2.1 混沌映射初始化种群

传统的群智算法采用随机方式初始化种群，不同的随机映射使种群有不同的空间分布，其结果直接影响算法的性能。而混沌运动具有遍历性和伪随机性[10]，混沌映射初始化种群应较常规的方法具有遍历空间的优势。

如图1所示，Logistic序列和Chebyshev序列为混沌序列，rand函数为Matlab默认随机序列函数。从散点图可以看出：混沌序列与rand函数相比在边界取值上更容易实现，遍历性更好。而Chebyshev混沌序列[11]的自相关函数更好，其迭代公式

X(t+1)=cos(warccos(x(t)))

(9)

式中w为Chebyshev的分形参数。改进算法采用Chebyshev混沌映射初始化种群。

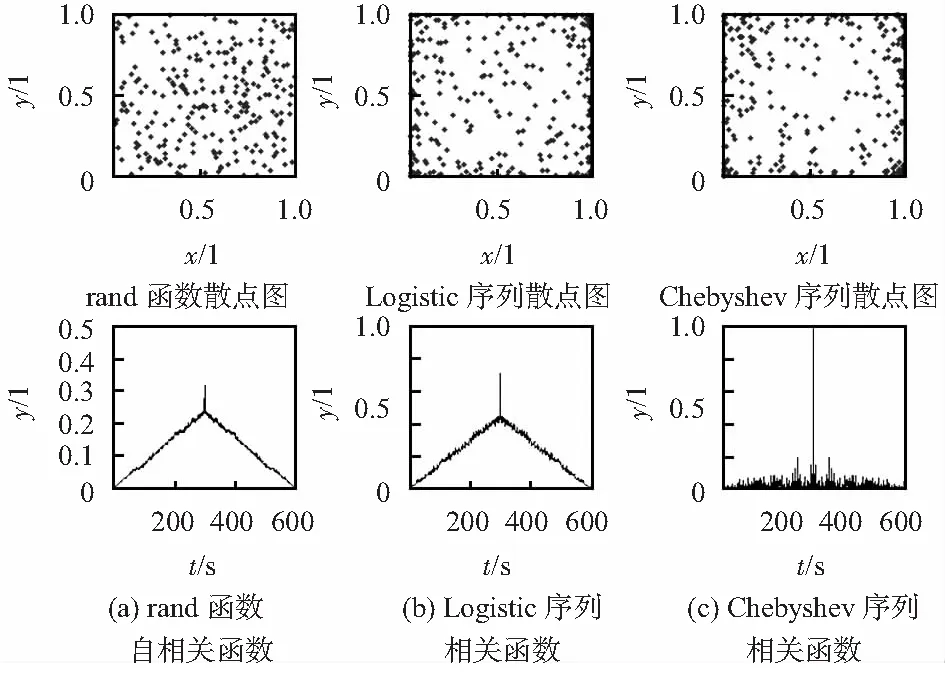
图1 混沌映射散点图及自相关函数

2.2 自适应调整搜索策略

搜索阶段，个体根据概率阈值p改变随机选择的变量值[12]，如式(10)

p=0.5(1-t/tmax)

(10)

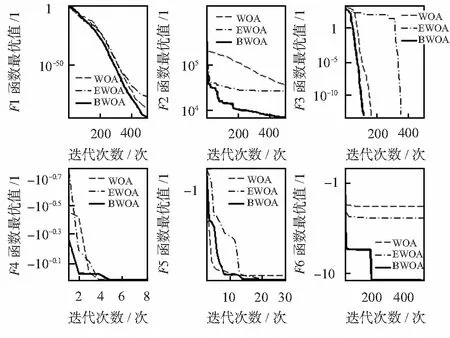
式中t为当前迭代次数；tmax为最大迭代次数。对每个搜索代理，以一个[0,1]随机数q与概率阈值p进行比较。当q

Xj=Xjmin+r·(Xjmax-xjmin)

(11)

式中r为[0,1]随机数;xjmin,xjmax为变量xj取值的最小值和最大值。

3 基准函数测试与分析

为了测试算法的收敛速度和全局优化能力，选择单峰和多峰的无约束测试函数[1,4]进行仿真，如表1所示，其中，F1，F2为单峰值函数，其余为多峰值函数。实验采用Matlab 2014a进行仿真，选择相同参数：种群个体数50，迭代次数500。

表1 基准测试函数

BWOA、WOA、高效WOA(EWOA)[2]的平均收敛曲线如图2所示，其中F4和F5函数经过了局部放大。

图2 基准测试函数收敛曲线

从图中各函数的收敛曲线可以看出:BWOA相较于标准WOA和EWOA，在单峰函数和多峰函数寻优过程中，均具有较快的收敛速度，能有效节约寻优的时间。从多峰函数的寻优过程可以看出，典型的如F5和F6函数，BWOA相较于标准WOA和EWOA，能够有效地避免局部收敛，更易获得全局最优解。

4 结 论

BWOA算法利用混沌特有的遍历性和伪随机性对鲸鱼算法初始化种群的优化，使种群个体在搜索阶段能够均匀分布并遍历整个搜索空间；自适应调整搜索策略，能更好地完成搜索空间的搜索。BWOA既保留了鲸鱼算法简单高效的优点，同时引入混沌机制和自适应机制实现仿生策略优化，实现对优化算法全局寻优能力和收敛速度的提升。

[1] Mirjalili S,Lewis A.The whale optimization algorithm[J].Advances in Engineering Software,2016,95:51-67.

[2] Ebrahimi A,Khamehchi E.Sperm whale algorithm:An effective metaheuristic algorithm for production optimization problems[J].Journal of Natural Gas Science and Engineering,2016,29:211-222.

[3] Kaveh A.Advances in metaheuristic algorithms for optimal design of structures[M].New York:Springer Verlag,2015.

[4] 倪 壮,肖 刚,敬忠良,等.改进蚁群算法的飞机冲突解脱路径规划方法[J].传感器与微系统，2016，35(4)：130-133.

[5] Yu Ting,Wang Limin,Han Xuming,et al.Swarm intelligence optimization algorithms and their application[C]∥Proceedings of Fourteenth Wuhan International Conference on E-Business,WHICEB 2015,Wuhan,China,2015:1-9.

[6] Das S,Biswas A,Dasgupta S,et al.Foundations of computational intelligence[M].Berlin Heidelberg:Springer,2009:23-55.

[7] Yang X S.Firefly algorithms for multimodal optimization[C]∥International Symposium on Stochastic Algorithms,2009:169-178.

[8] 郑洪清,周永权.一种自适应步长布谷鸟搜索算法[J].计算机工程与应用,2013,49(10):68-71.

[9] 霍慧慧,李国勇.改进的离散果蝇优化算法在WSNs覆盖中的应用[J].传感器与微系统，2016,35(2)：157-160.

[10] 许 栋,崔小欣,王 田,等.基于Logistic映射的混沌随机数发生器研究[J].微电子学与计算机,2016,33(2):1-6.

[11] Zhou Y,Zhou J,Wang F,et al.An efficient chaotic map-based authentication scheme with mutual anonymity[J].Applied Computational Intelligence and Soft Computing,2016,10:1-8.

[12] Kaveh A,Ghazaan M I.Enhanced whale optimization algorithm for sizing optimization of skeletal structures[J].Mechanics-based Design of Structures and Machines,2017,45:345-362.

Studyofwhalealgorithmforbiomimeticstrategyoptimization*

GONG Shi-bing, SHEN Hai-bin

(InstituteofVLSIDesign,ZhejiangUniversity,Hangzhou310027，China)

The whale optimization algorithm(WOA)is inspired by the hunting behavior of humpback whales and it’s presented as a new swarm-based optimization algorithm recently.This study proposes an improved whale optimization algorithm with optimization strategy of bionics(BWOA)by Chaos mapping initialization population and adaptive adjusting search strategy,in order to improve the accuracy of global optimization and the rate of convergence.By simulation on reference test function,BWOA is compared with standard WOA and effective WOA(EWOA),efficiency of BWOA,is demonstrated.

whale optimization algorithm(WOA); biomimetic strategy; swarm-based optimization algorithm; Chebyshev sequences; initial population based on Chaos mapping

10.13873/J.1000—9787(2017)12—0010—03

TP 301

A

1000—9787(2017)12—0010—03

2017—01—04

国家“863”计划资助项目(2012AA041701)

巩世兵(1985-)，男，硕士研究生，主要研究方向为智能安全与芯片设计。沈海斌，男，教授，博士生导师，主要从事智能算法、安全处理器架构及其实现等方面的研究工作。