基于灰色回归组合模型的铁路客运量预测研究

王 彬

(天津大学 管理与经济学部， 天津 300072)

基于灰色回归组合模型的铁路客运量预测研究

王 彬

(天津大学 管理与经济学部， 天津 300072)

铁路客运量是衡量我国交通需求的重要指标，科学预测铁路客运量是制定交通发展规划的重要依据。鉴于组合模型能克服单一模型的不足并兼具单一模型的优点，基于灰色模型和线性回归模型，根据灰色关联度赋予单一模型相应权重，建立铁路客运量组合预测模型，并选取2006—2015年铁路客运量数据，对我国铁路客运量进行预测。结果表明：组合模型克服了单一模型的预测局限性，能进一步提高预测精度，适用于铁路客运量预测研究。

灰色模型；线性回归模型；组合模型；铁路客运量

铁路作为一种现代化运输方式，是一个国家经济发展水平高低的集中体现。同时，国民经济的发展也离不开铁路运输业的发展，两者相辅相成。随着我国经济的迅猛发展，我国铁路运输能力不断增强，铁路客运量不断增长，这就要求我们合理制定铁路运输计划、科学预测铁路客运量。作为铁路运输组织工作的重要基础，铁路客运量预测的准确性不仅影响着铁路运输资源配置效率，更影响着铁路运输发展规划的制定，关乎我国铁路运输业的健康发展，具有举足轻重的现实意义。

在铁路客运量预测方面，国内学者提出了多种预测模型。刘殿胜[1]对我国铁路客运量运距构成进行了分析，为铁路客运量预测打下了良好基础。王卓等[2]利用改进的BP神经网络对铁路客运量时间序列进行分析，得到了相对满意的预测结果。郝军章等[3]利用SARIMA模型对我国铁路客运量季节时间序列进行研究，拟合结果表明预测精度相对较好。侯立新[4]利用指数平滑法对京包线旅客发送量进行预测，通过分析旅客发送量时间序列发现运用二次指数平滑模型进行预测是科学合理的。田桂英等[5]基于GM(1,1)残差模型对广西壮族自治区铁路客运量进行预测，结果表明：GM(1,1)残差模型能利用较少的数据得到精度较高的预测数据。李晓东[6]基于线性回归-马尔可夫模型对我国铁路客运量进行预测，结果表明：线性回归-马尔可夫模型在铁路客运量预测方面还有待进一步完善。

通过对以上模型进行分析发现：目前常用的铁路客运量预测模型都比较依赖于大量历史数据的分析，而铁路系统又是一个包含众多未知信息的多因素开放式系统，这正属于灰色系统的大范畴，因此灰色GM(1,1)铁路客运量预测模型可以利用较少已知数据得到精度较高的预测结果。考虑到灰色GM(1,1)模型在处理一些具有线性变化趋势的数据方面具有一定的局限性，如果能结合线性回归模型，将会进一步降低预测误差，改善预测结果。本文基于灰色GM(1,1)模型和线性回归模型，根据灰色关联度赋予单一模型相应权重，在此基础上建立铁路客运量组合预测模型对我国铁路客运量进行预测，以便得到精度更高的预测结果。

1 灰色回归组合模型的建立

1.1 灰色模型

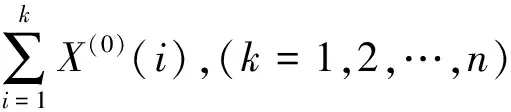
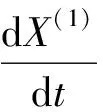
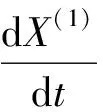
通过灰色GM(1,1)模型的建立过程可以看出，原始数据的光滑度和背景值公式的构造直接影响着模型的预测准确性，如果原始数据不够光滑或者模型背景值与实际背景值不够协调，这种情况下灰色GM(1,1)模型的预测误差就相对较大[7]。

1.2 线性回归模型

线性回归模型是用一个或多个解释变量来解释因变量的一种计量模型。不妨设Y为因变量，X1，X2，…,Xn为n个用来解释Y的解释变量，称方程Y=β0+β1X1+…+βnXn,(i=1,2,…,k) 为线性回归模型，其中β0为常数项，参数β1,β2,…,βn称为回归系数。

若令

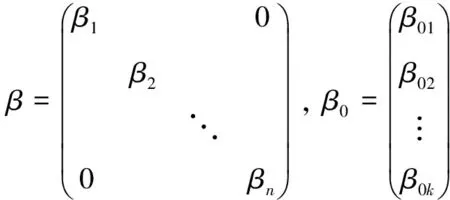
(1)

则一元线性回归模型可用矩阵形式表示为：Y=β0+βX，其中：β0为常数项；参数β1,β2,…,βn称为回归系数。

1.3 组合模型

灰色GM(1,1)模型在处理具有指数增长趋势的原始数据方面预测精度很高，而对线性变化的原始数据预测效果不是很好；线性回归模型在处理线性变化的原始数据方面预测精度很高，而对具有指数增长趋势的非线性变化数据预测效果不佳。如果原始数据既有一定的线性变化，又有一定的指数增长趋势，那么单独利用灰色GM(1,1)模型或线性回归模型都很难得到满意的预测结果。

通过将灰色GM(1,1)模型和线性回归模型进行组合，建立的组合预测模型既能处理具有指数增长趋势的原始数据，又能处理具有线性变化的原始数据，在一定程度上大大降低了单独利用灰色GM(1,1)模型或线性回归模型的预测误差。本文基于灰色关联度分别赋予灰色GM(1,1)模型和线性回归模型一定的权重，在此基础上建立组合预测模型[15-21]：

k=1,2,…,n

w1+w2=1

(2)

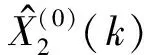
(3)

令

(4)

则

(5)

从灰色关联度定义可以看出：Δ(k)表示模型预测值和实际值的预测误差，灰色关联度表示模型预测值和实际值的相似程度，只有当预测值和实际值完全相同时，灰色关联度才为1。

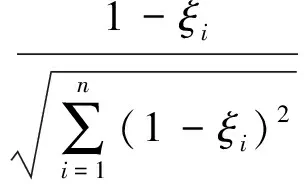
1.4基于灰色回归组合模型的铁路客运量预测

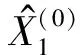
k=1,2,…,n

w1+w2=1

(6)

利用Matlab等数学工具求解该灰色回归组合模型，计算GM(1,1)模型和线性回归模型的权重系数分别为w1=0.169 2，w2=0.830 8，得到我国铁路客运量预测结果，如表1所示。

表1 我国铁路客运量预测

通过表1可以看出:2006年以来，我国铁路客运量一直保持着高速发展，截至2015年，铁路客运量已达到253 484万人;同时，基于GM(1,1)模型的预测值平均相对误差为4.77%，基于线性回归模型的预测值平均相对误差为3.07%，而基于灰色回归组合模型的预测值平均相对误差为2.95%。

通过对比发现，2006—2010年灰色GM(1,1)模型的预测误差小于线性回归模型的预测误差，说明这段时间铁路客运量保持着较为明显的指数增长趋势；2011—2015年灰色GM(1,1)模型的预测误差大于线性回归模型的预测误差，说明这段时间铁路客运量保持着较为明显的线性增长趋势。因此，我国铁路客运量发展既有一定的指数增长趋势，又有一定的线性增长趋势，利用单一模型对我国客运量进行预测存在着一定的预测局限性，单一模型不能准确反映我国铁路客运量的发展趋势。

同时，灰色回归组合模型的预测平均误差要小于灰色GM(1,1)模型和线性回归模型的预测平均误差；由于线性回归模型预测值保持线性增长趋势，随着我国铁路客运量的迅猛发展，自2014年开始，线性回归模型预测值小于实际值，考虑到灰色GM(1,1)模型预测值大于实际值，使得2014—2015年灰色回归组合模型的预测误差均小于灰色GM(1,1)模型和线性回归模型的预测误差。由此可以预见，在未来几年灰色回归组合模型的预测误差都将小于单一模型的预测误差。因此，灰色回归组合模型兼顾了铁路客运量的线性增长趋势和指数增长趋势，克服了单一模型的预测局限性，进一步降低了预测误差，提高了预测准确性。

2 结束语

铁路作为一种现代化运输方式，是一个国家经济发展水平高低的集中体现。同时，国民经济的发展也离不开铁路运输业的发展，两者相辅相成。随着我国经济的迅猛发展，我国铁路运输能力不断增强，铁路客运量不断增长，这就要求我们合理制定铁路运输计划，科学预测铁路客运量。本文基于灰色GM(1,1)模型和线性回归模型，根据灰色关联度赋予单一模型相应权重，在此基础上建立铁路客运量组合预测模型，并选取2006—2015年这10年间的铁路客运量数据，对我国铁路客运量进行预测。结果表明，基于GM(1,1)模型的预测值平均相对误差为4.77%，基于线性回归模型的预测值平均相对误差为3.07%，而基于灰色回归组合模型的预测值平均相对误差为2.95%，克服了单一模型的预测局限性，进一步降低了预测误差，提高了预测准确性。

[1] 刘殿胜.铁路客运量分析探讨[J].中国铁路，2008(9):7-9.

[2] 王卓，王艳辉，贾利民,等.改进的BP神经网络在铁路客运量时间序列预测中的应用[J].中国铁道科学，2005，26(2):127-131.

[3] 郝军章，崔玉杰，韩江雪.基于SARIMA模型在我国铁路客运量中的预测[J].数学的实践与认识，2015，45(18):95-104.

[4] 侯立新.基于指数平滑法的京包线铁路客运量预测[J].科技创新导报，2012(32):107-107.

[5] 田桂英，王花兰.基于GM(1,1)残差模型的铁路客运量预测[J].价值工程，2010，29(18):252-253.

[6] 李晓东.基于线性回归-马尔可夫模型的铁路客运量预测[J].铁道运输与经济，2012，34(4):38-41.

[7] 何海，陈绵云.GM(1,1)模型预测公式的缺陷及改进[J].武汉理工大学学报，2004，26(7):81-83.

[8] 张磊，孙长青.高阶残差修正GM(1,1)区间预测模型及其应用[J].兵器装备工程学报，2017，38(2):177-181.

[9] 杨克磊，张振宇，和美.应用灰色GM(1,1)模型的粮食产量预测研究[J].重庆理工大学学报(自然科学)，2015(4):124-127.

[10] 彭岩，杨卓毅.基于改进GM(1,1)模型的天津市电力消费预测研究[J].重庆理工大学学报(自然科学)，2015，29(1):131-134.

[11] 卞艺杰，李杭.基于GM(1,1)模型的南京市电力需求预测与探究[J].重庆理工大学学报(自然科学)，2016，30(7):69-73.

[12] 严超，张安明，吴仕海.基于 GM(1,1)模型的土地生态安全动态分析与预测——以安徽省池州市为例[J].西南大学学报(自然科学版)，2015，37(2):103-109.

[13] 朱岚.基于灰色GM(1,1)联合预测模型的企业产值评估[J].重庆理工大学学报(自然科学)，2016，30(10):175-180.

[14] 游中胜，何丽.基于序列包络带的 GM(1,1)区间预测建模条件研究[J].西南大学学报(自然科学版)，2015，37(1):150-154.

[15] 刘思峰，曾波，刘解放,等.GM(1,1)模型的几种基本形式及其适用范围研究[J].系统工程与电子技术，2014，36(3):501-508.

[16] 杨华龙，刘金霞，郑斌.灰色预测GM(1,1)模型的改进及应用[J].数学的实践与认识，2011，41(23):39-46.

[17] 高连生，易诞，毛娜,等.基于改进的GM(1,1)的长期交通量预测模型[J].铁道科学与工程学报，2015(1):203-207.

[18] 钟霞，吴中，王丽.灰色理论及其组合模型在交通运量预测中的运用[J].交通标准化，2004(12):35-38.

[19] 沈阳武，彭晓涛，施通勤,等.基于最优组合权重的电能质量灰色综合评价方法[J].电力系统自动化，2012，36(10):67-73.

[20] 彭保发，胡曰利，吴远芬,等.基于灰色系统模型的城乡建设用地规模预测——以常德市鼎城区为例[J].经济地理，2007，27(6):999-1002.

[21] 马星河，闫炳耀，唐云峰,等.基于优选组合预测技术的中长期负荷预测[J].电力系统及其自动化学报，2015，27(6):62-67.

(责任编辑刘 舸)

ForecastofRailwayPassengerTrafficBasedonGreyLinearRegressionCombinedModel

WANG Bin

(Department of Management and Eeconomics, Tianjin University, Tianjin 300072， China)

Railway passenger traffic is an important index to measure the demand of transportation in our country. Scientific forecast of railway passenger traffic is an important basis for the development of transportation development planning. In order to accurately predict the passenger capacity of our country, this paper establishes the grey linear regression combined model for railway passenger traffic, based on the gray model and the linear regression model, to which corresponding weight is given according to the gray correlation degree, and select the of 2006—2015 railway passenger traffic to forecasting our Railway Passenger Traffic. The results show that the combined model overcomes the prediction limitations of the single model and has a wide range of application, which can further improve the prediction accuracy and can be used to predict the railway passenger traffic.

grey model；linear regression model；combined model；railway passenger traffic

2017-03-26

天津市应用基础及前沿技术研究计划资助项目“基于感知过程的复杂系统信息融合理论与应用研究”(10JCYBJC07300)

王彬(1973—)，男，海南临高人，硕士，主要从事管理科学与工程研究，E-mail:wangbin1973@zoho.com。

王彬.基于灰色回归组合模型的铁路客运量预测研究[J].重庆理工大学学报(自然科学)，2017(11):230-234.

formatWANG Bin.Forecast of Railway Passenger Traffic Based on Grey Linear Regression Combined Model[J].Journal of Chongqing University of Technology(Natural Science)，2017(11):230-234.

10.3969/j.issn.1674-8425(z).2017.11.035

O212

A

1674-8425(2017)11-0230-05