基于一维假设的瞬态换热实验的误差修正

王 蕾,马庆辉，罗 翔

(1.西安理工大学 机械与精密仪器工程学院， 西安 710048; 2.中国涡轮研究院， 成都 610500; 3.北京航空航天大学 能源与动力工程学院， 北京 100191)

基于一维假设的瞬态换热实验的误差修正

王 蕾1,马庆辉2，罗 翔3

(1.西安理工大学 机械与精密仪器工程学院， 西安 710048; 2.中国涡轮研究院， 成都 610500; 3.北京航空航天大学 能源与动力工程学院， 北京 100191)

使用热色液晶测量涡轮旋转盘腔表面温度随时间的变化，即利用一维半无限大平板的非稳态导热理论求出盘面的对流换热系数。然而，该理论忽略了盘面横向温度不均的影响。针对一维平板的假设在实际工程中由于盘面温度分布而导致的横向热传导所带来的误差进行理论分析得到修正方法，在25 ℃下采用带宽为1 ℃的热色液晶进行实验，将一维平板假设计算得到的对流换热系数和修正后的对流换热系数进行对比分析。研究发现：盘面的量纲一过余温度在0.44～0.55的范围内时，使用窄幅液晶测量盘面量纲一半径为0.77～0.94的对流换热系数时，由于横向热传导而带来的误差可控制在1.5%以内。

热色液晶; 瞬态实验；旋转盘腔；横向热传导；误差

稳态换热实验对测试仪器的要求相对较高，且实验时间长、资源投入大。而瞬态换热实验方法正好相反，尤其是配合热色液晶的使用后，优越性更为明显，并在近些年来得到了很好的应用和发展。热色液晶具有能在一定的温度范围内显示特定颜色的性质，根据显色的温度范围可分为窄幅热色液晶和宽幅热色液晶。窄幅热色液晶的带宽通常为1 ℃左右，测温误差为0.1 ℃；而宽幅热色液晶的带宽为10 ℃，测温误差比窄幅液晶更大。

在瞬态换热实验中，通常利用窄幅的热色液晶测量表面温度，获取温度随时间的变化关系，即可从一维傅里叶导热方程的理论解中计算得到物体表面的对流换热系数。热色液晶已用于瞬态实验的研究中，如Ireland[1]最早在瞬态法测量对流换热系数上使用热色液晶。Jones[2]将热色液晶瞬态法测量得到的值与稳态法测量得到的值及理论计算值进行对比，论证了瞬态法的可信度。Baughn[3]使用热色液晶测量计算了复杂部件表面湍流流动时的换热系数。

热色液晶的另外一个优势在于可以用来测量旋转部件表面的温度场。旋转部件换热实验研究的主要难点，在于对温度场、流场的测量时实现测试信号的动静转化。传统的测量旋转部件表面温度的方法为使用热电偶或红外测温仪，但由于旋转使得这2种方法的测试装置复杂且测温精度不高。Newton[4]使用热色液晶配合频闪照明拍摄系统克服传统旋转测试系统的缺点并准确地测量旋转盘表面局部温度。此后，热色液晶在涡轮盘腔的换热实验中得到广泛应用。Lock[5]使用热色液晶对带预旋的转静系盘腔内换热特性进行了实验研究。

对于热色液晶在瞬态实验的误差，学者从测量的每个参数着手分析了实验误差。温度测量的误差会增大对流换热系数的误差，Yan[6]估算了瞬态实验误差并提出了减小误差的方法,通过分析结果发现：根据气体初始温度和阶跃后温度选择适当的液晶显色温度范围，并且使量纲一过余温度介于0.3～0.7，可以保证瞬态实验方法的可信度。Owen等[7-9]使用液晶并采用瞬态法对涡轮盘腔转静系的各种结构进行了局部换热系数的测量和数值计算。

已有的瞬态实验求解对流换热系数均基于一维半无限大平板的假设开展，即假设温度只沿壁面的法向发生变化，而这在实际工程中是不存在的。虽然通过调整实验参数，如合理选择实验件的材料和厚度使其满足无穿透的条件、合理设置温度分布可以有效控制实验的误差，但当横向温度分布的差异较大时，横向的热传导不能忽略。Lin[10]、Ling[11]利用数值的方法求解了三维傅里叶导热方程，发现一维假设在存在横向热传导的条件下给对流换热系数带来的误差为15%～20%，根据研究结果提出了相应的热色液晶用于瞬态实验减小实验误差的方法。

本文对一维半无限大平板假设带来的系统误差进行分析，通过求解二维傅里叶导热方程提出对流换热系数修正方法，利用修正的公式计算对流换热系数可避免在具体的实验中求解复杂的二维和三维傅里叶方程，具有较强的工程实践指导意义。此外，一个盘面的量纲一过余温度在0.44～0.55的范围内时，使用窄幅液晶(R25C1W)测量盘面量纲一半径为0.77～0.94的对流换热系数的瞬态实验中，将根据一维假设得到的值与修正后的值进行对比分析，得到了一定条件下的横向热传导的误差。

1 瞬态实验原理

瞬态实验的理论依据为一维半无限大平板(如图1所示)的换热理论，在x=0界面有温度为T0气流流过，整个流动换热的过程处于热平衡状态。设物体的密度为ρ、导热系数为λ、比热容为c，描述此问题的导热微分方程、初始条件和边界条件为：

(1)

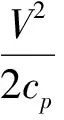
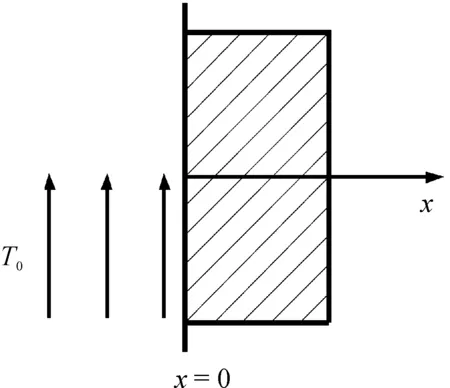
图1 一维半无限大平板

当主流绝热壁温Taw(τ)确定后，对式(1)使用拉普拉斯变换和分离变量法[12]可求得T(x,τ)的解析解，这样即可知壁温Tw(即x=0)与时间τ及换热系数h的关系式。据此，通过瞬态实验方法测得τ与Tw的对应值后，即可通过数值方法求出h。

对于不同形式的主流温度Taw(τ)(如图2所示，Tf(τ)形式也一致)，由式(1)求解所得的Tw形式不同。

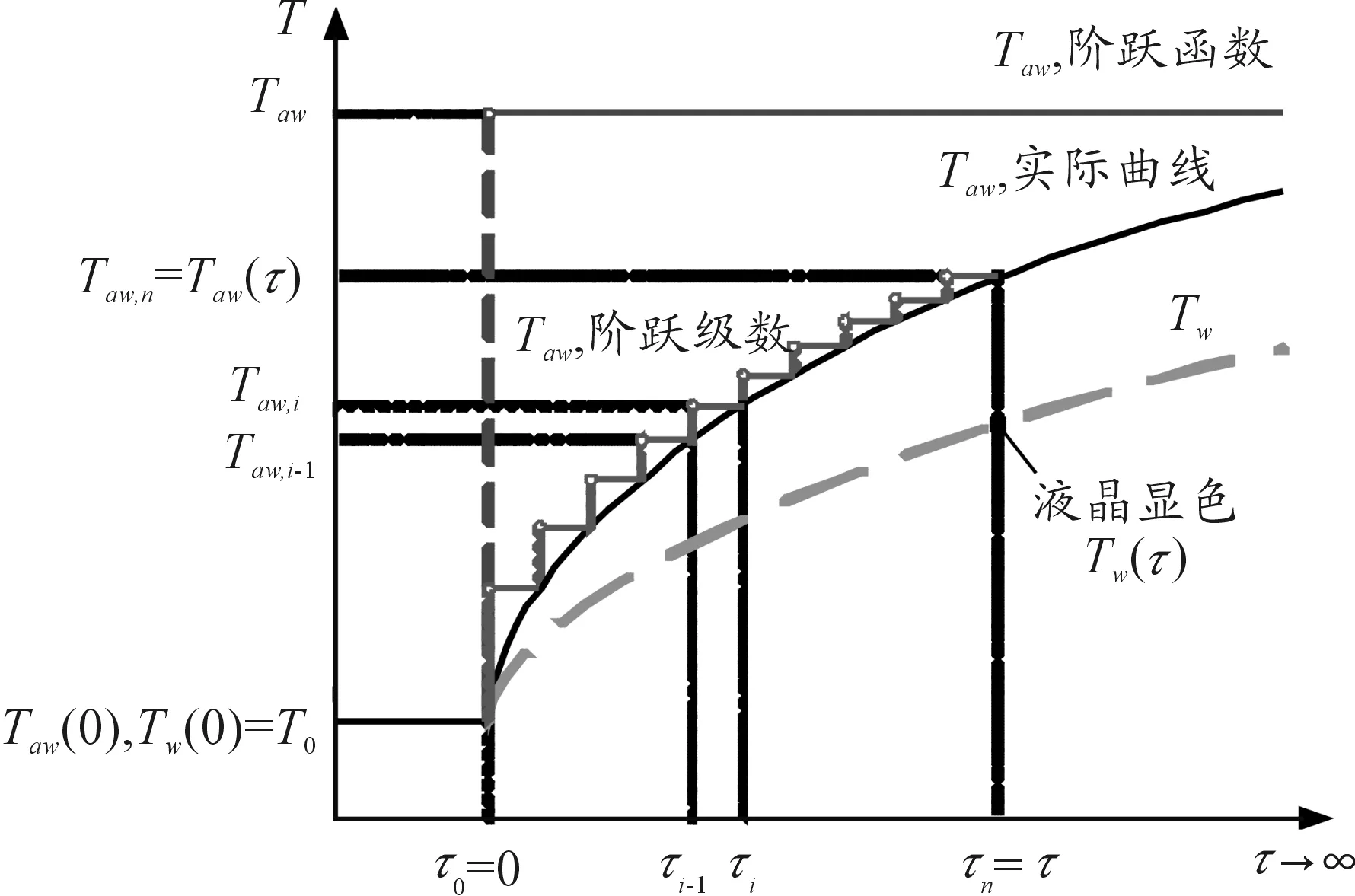
图2 主流和壁面温度的时间曲线

当Taw为阶跃函数时，即有：

(2)

在此主流温度条件下，Tw(τ)的解为[13-14]：

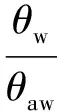
(3)

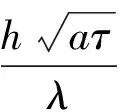
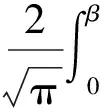
(4)

式(3)是最经典的瞬态法换热实验的理论依据，该分析解在形式上最为简单。但是，在瞬态换热实验中，主流的加热在技术上很难实现Taw(或Tf)的瞬间提升。通常情况下，主流温度需要一段时间才能达到稳定状态(如图2中Taw的实际温升曲线)，若此时换热实验数据仍采用阶跃温升的理论解进行处理，则会带来较大的模型误差。对此，一个较好的近似方法是将主流温度Taw(τ)处理为阶跃级数形式，即：

(5)

式中:n为阶跃级数的项数，且τ0=0，τn=τ。n=1时，式(5)与式(2)相同；n→∞时，Taw(τ)趋于实际主流温升曲线。对此，由式(1)求得Tw(τ)的解为[15]：

(6)

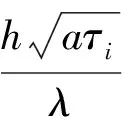
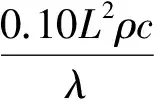
2 横向热传导的误差分析

为了考虑横向温差带来的误差，需求解傅里叶二维导热方程，表示如下：

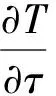
(7)

式中：x是垂直于测量固体表面的方向；y是平行于测量固体表面的方向；λ为导热系数；ρ为固体的密度；cp为固体的定压比热容。

当∂2T/∂y2=0时，就是求解对流换热系数h的半无限大平板假设的一维傅里叶导热方程。

定义量纲一参数并对一维傅里叶方程进行量纲一化：

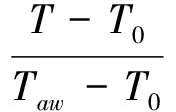
Fo=aτ/L2，Bi=hL/λ

那么式(3)可以写为

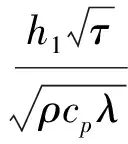
(8)

式中：Fo为傅里叶数；Bi1为一维傅里叶导热方程求得的毕渥数；h1为对流换热系数；L是固体的厚度；a(λ/ρcp)为热扩散率。

对二维傅里叶导热方程式(7)进行无量纲化：

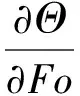
(9)

定义一个参数φ，使

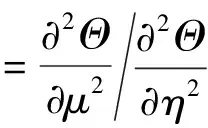
(10)

将式(10)代入到式(9)中，那么式(9)就可以简化为包含μ与η两个方向的一维傅里叶导热方程：

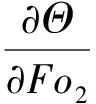
(11)

其中

Fo2=Fo(1+φ)

(12)

式(12)中φ包含y方向上的导热，那么类比一维半无限大平板假设的分析解，式(11)的解为

(13)

其中

(14)

Bi2、h2分别是二维傅里叶导热方程中的毕渥数和对流换热系数。

由式(8)(12)(14)可知：

Bi2=Bi1(1+φ)-1/2

(15)

那么就可以通过一维导热方程中已求得的Bi1求Bi2，从而可以求得对流换热系数h2，即对横向温差产生的热传导进行修正后的对流换热系数。

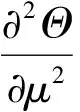
3 对流换热系数修正

James和Lock[16]对求φ值做了详细的理论推导和实验验证研究。

先假设

φ=cφ0

(16)

然后通过理论推导得到：

(17)

(18)

最后通过实验得到c与Θ的经验关系式：

c=0.563-0.371Θ

(19)

其中Fo0是液晶变色时的傅里叶数。

所以由式(16)～(19)可以得到φ值，再通过式(15)和由一维傅里叶导热方程求得的Bi1可以求得修正过的对流换热系数h2。

本文利用瞬态方法测量图3所示涡轮盘腔转静系中旋转盘面的对流换热系数，该转静系为实际发动机涡轮盘腔简化缩放之后得到的结构。测试区域位于盘面径向位置介于ab之间的扇形区域， ab的径向长度为34.5 mm，无量纲半径范围为0.857～0.948。气流通过静止盘上的预旋孔进入盘腔，采用电焊机作为电源的电加热器，为流经实验件表面的气流提供一个阶跃的温升。实验件测量表面喷涂的液晶为25 ℃的窄幅热色液晶(R25C1W)，用相机配合频闪仪记录盘面热色液晶的显色过程。具体实验设备和方法参见徐国强[17]在北京航空航天大学航空发动机气动热力国家级重点实验室的旋转换热多功能实验台上开展的瞬态换热测量盘面对流换热系数的实验。

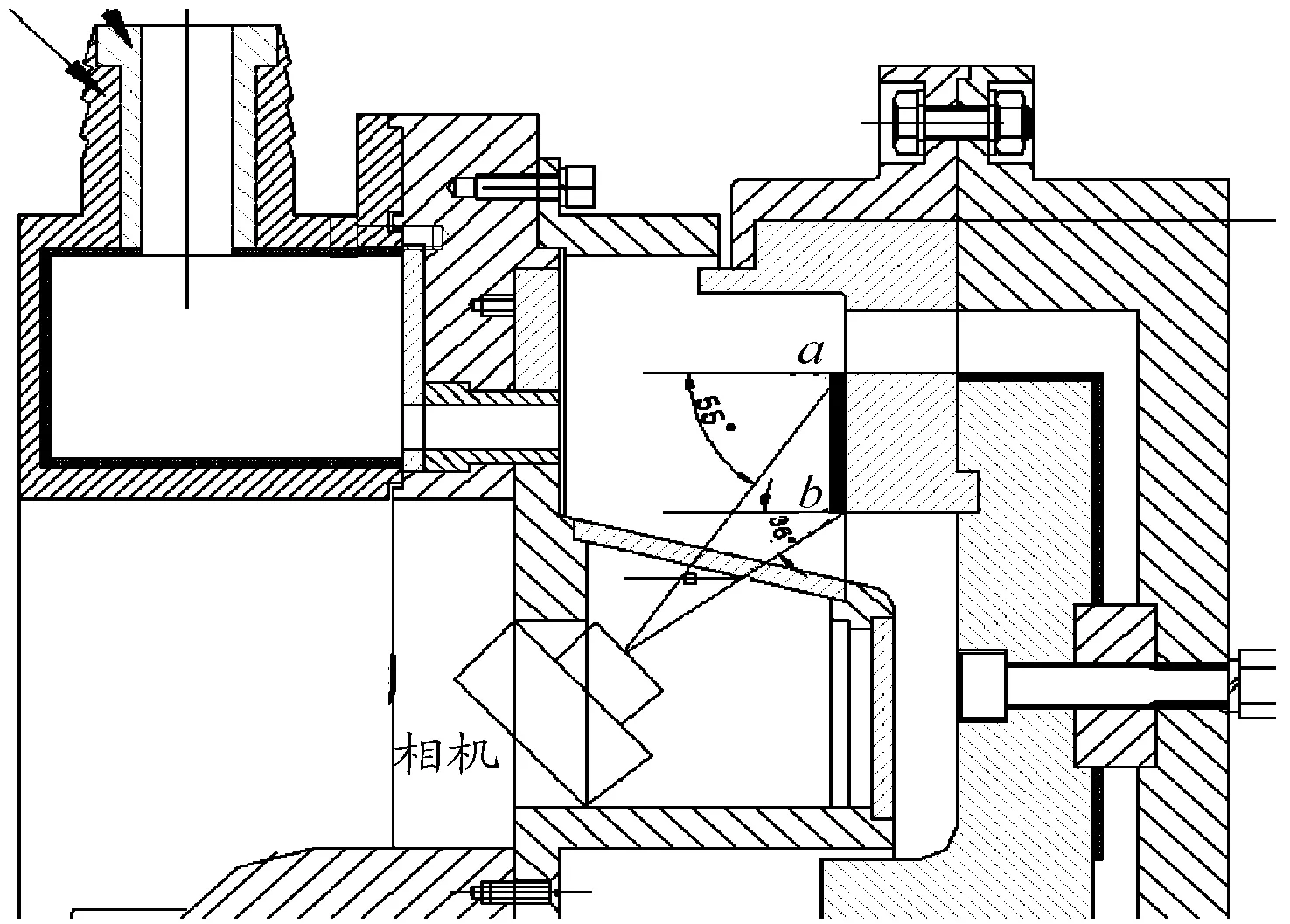
图3 瞬态换热实验件

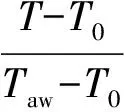
本文对考虑横向误差之后的修正值和未修正值进行对比分析，基于半无限大平板假设理论求得的对流换热系数为修正之前的数据，由二维傅里叶导热方程求得的对流换热系数为考虑热传导修正后的数据。

选取旋转盘腔进气流量700 kg/h，转速分别为0、500、1 000、1 500、2 000 r/min 5个工况的对流换热系数h进行修正。选取测试区域径向的一条直线上的对流换热系数，并按照以下的方法计算考虑横向热传导的修正值：

1) 利用式(3)～(6)，即基于半无限大平板假设理论由实验结果求得Bi1。

2) 使用最小二乘法3次样条插值对已求得沿半径的Bi1进行拟合。在处理数据过程中，每个工况拟合度都在0.95以上。

3) 由拟合后的曲线可以求得每个点的∂Bi1/∂μ和∂2Bi1/∂μ2值，然后代入式(17)中可以求得φ0。其中Fo0是从加热时刻开始，到主盘温度开始变色之间的时间段对应的傅里叶数。将0、500、1 000、1 500、2 000 r/min 5个工况对应的时间代入Fo0的公式计算，得到每个工况对应的Fo0分别为0.026、0.011 1、0.008 97、0.005 69、0.003 8。

4) 定该工况的无量纲过余温度Θ=0.462，代入式(19)可以得到c=0.390 75。

5) 将求得的每个点的Bi1、φ0、c代入式(15)和式(16)中可以求得修正后的每个点对应的Bi2，进而求得修正后的对流换热系数h2。

由于每个工况半径方向上的点很多，因此对每个点进行人工修正耗时比较长，故编写VB程序对其进行批处理。修正后的数值与修正前的数值如图4所示。

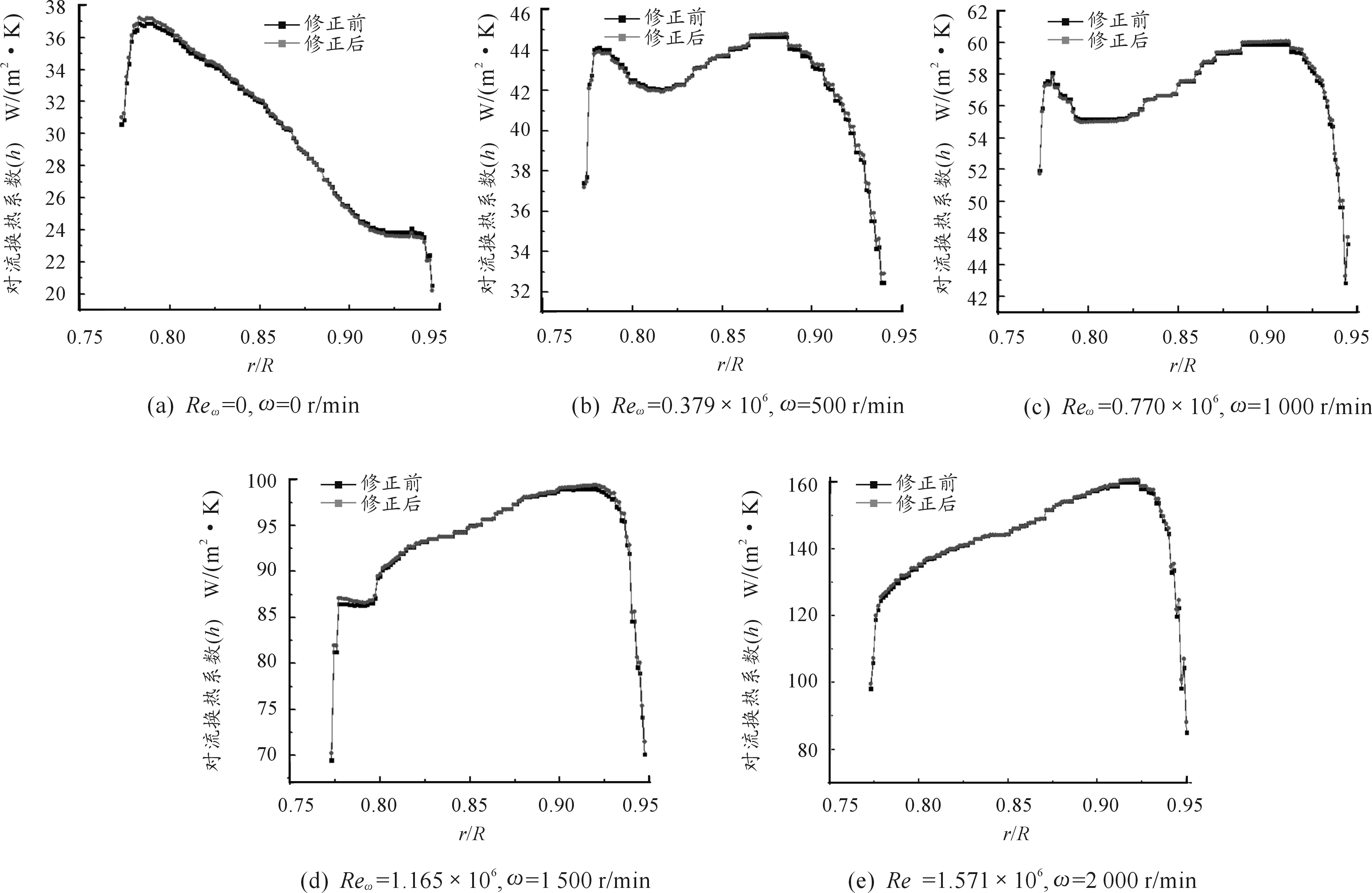
图4 m=700 kg/h，修正前后的对流换热系数对比

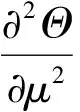
从图4中可以看出：在本实验的条件下，基于一维半无限大导热理论得到的修正前的值与修正后的值的误差不超过5%。这主要是因为，窄幅液晶显色温度范围为1 ℃，液晶拍摄视野即量纲一半径0.77～0.94都有液晶显色，所以该区域的温差最大为1 ℃。那么，由热传导引起的误差就会相对小一些。Yan等[6]对半无限大平板假设后的一维求解分析出的实验误差在量纲一过余温度0.3<Θ<0.7范围内为5%，由此可知该热传导误差相对其实验测量误差较小，即在其测量误差范围内。所以采用窄幅液晶进行瞬态换热实验时，热传导误差可以不予考虑。可以推断，当换热表面温差较大时，热传导因素对基于半无限大平板假设求得的对流换热系数影响就会很大。因此，在大温差换热平面上，该对流换热修正理论有很好的应用。为了深入分析转速对横向热传导带来的误差影响以及该误差随量纲一半径的变化规律，定义Δ=|h2-h1|/h1。图5给出了500、1 000、1 500、2 000 r/min 4个工况下误差Δ随量纲一半径的变化规律。

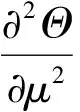
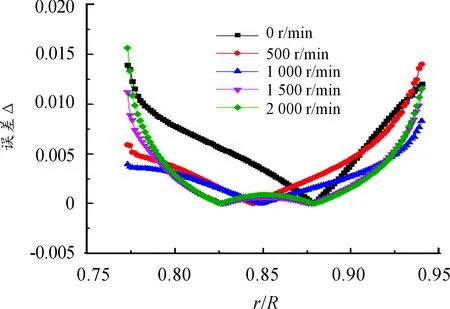
图5 各个工况误差Δ随量纲一半径变化

4 结论

通过二维傅里叶导热方程对横向热传导的误差进行了分析，并且结合实验结论，得到了修正的经验公式。在求解修正值时，利用修正公式避免求解复杂的二维导热方程，即直接对瞬态换热实验计算得到的对流换热系数进行计算修正。通过修正前后值的对比，发现在过余温度满足0.44<Θ<0.55，使用1 ℃的窄幅液晶测量转盘量纲一半径为0.77～0.94的对流换热系数时，横向热传导带来的误差不超过1.5%。本文结论保证了一定条件下的瞬态实验的可靠性，对于更宽广的实验的修正也可以通过经验公式进行。

[1] IRELAND P T,JONES T V.The measurement of local heat transfer coefficients in blade cooling geometries[C]//AGARD Conference Proceedings.1985:28.

[2] JONES T V,HIPPENSTEELE S A.High-resolution heat-transfercoefficient maps applicable to compound-curve surfaces using liquid crystals in a transient wind tunnel[J].NASA Technical Memorandum,1988:89855.

[3] BAUGHN J W.Liquid crystal methods for studying turbulent heat transfer[J].Int J Heat Fluid Flow,1995,16:365-375.

[4] NEWTON P J,YAN Y,STEVENS N E,et al.Transient Heat Transfer Measurements Using Thermochromic Li-quid Crystal.Part 1:An Improved Technique[J].Int J Heat Fluid Flow,2003,24:14-22.

[5] LOCK G D,WILSON M,OWEN J M.Influence of Fluid Dynamics on Heat Transfer in a Pre-Swirl Rotating Disc System[Z].ASME Paper,GT2004-53158,2004.

[6] YAN Y,OWEN J M.Uncertainties in Transient Heat Transfer Measurements with Liquid Crystal[J].Int J Heat & Fluid Flow,2002,23:29-35.

[7] KARABAY H,WILSON M,OWEN J M.Predictions of effect of swirl on flow and heat transfer in a rotating cavity[J].Int J Heat & Fluid Flow,2001,22(2):143-155.

[8] KAKADE V U,LOCK G D,WILSON M,et al.Accurate heat transfer measurements using thermo chromic liquid crystal.Part 1:Calibration and characteristics of crystals[J].Int J Heat & Fluid Flow,2009,30:939-949.

[9] KAKADE V U,LOCK G D,WILSON M,et al.Accurate heat transfer measurements using thermo chromic liquid crystal.Part 2:Application to a rotating disc[J].Int J Heat & Fluid Flow,2009,30:950-959.

[10] LIN M,WANG T.A transient liquid crystal method using a 3-D inverse transient conduction scheme[J].Int J Heat Mass Transfer,2002,45:3491-3501.

[11] LING J P C W.A technique for processing transient heat transfer liquid crystal experiments in the presence of la-teral conduction.(2003-GT-38446)[J].Journal of Turbomachinery,2004,126(2):297-310.

[12] KAKAC S,YENER Y.Heat Conduction[M].2nd ed.Washington:Hemishpere Publishing Corporation,1985.

[13] SCHULTZ D L,JONES T V.Heat transfer measurements in short duration hypersonic facilities[M].USA:AGARDograph,1973,165.

[14] CLIFFORD R J,JONES T V,DUNNE S D.Techniques for Obtaining Detailed Heat Transfer Coefficient Measurements Within Gas Turbine Blade and Vane Cooling Passages[M].[S.l.]:ASME Paper,1983.

[15] METZGERetzger D E,LARSONarson D E.Use of Melting Point Surface Coatings for Local Convection Heat Transfer Measurements in Rectangular Channel Flows with 90-Deg Turns[J].Journal of Heat Transfer,1986,108(1):48-54.

[16] KINGSLEY J R,LOCK G D,OWEN J M.Transient heat transfer measurements using thermochromic liquid crystal:lateral-conduction error[J].International Journal of Heat and Fluid Flow,2005,26(2):256-2.

[17] 徐国强,赵熙,罗翔,等.直接供气预旋转静系的换热[J].航空动力学报,2012,27(10):2161-2168.

(责任编辑林 芳)

ErrorCorrectionofTransientHeatTransferExperimentBasedonOneDimensionalHypothesis

WANG Lei1， MA Qinghui2， LUO Xiang3

(1.School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China；2.China Gas Turbine Establishment, Chengdu 610500, China;3.School of Power and Energy, Beihang University, Beijing 100191, China)

Knowing the time at which the termochromic liquid crystal (TLC) changes color, then the heat transfer coefficient can be calculated applying the analytical solution of one-dimensional semi-infinite plate hypothesis transient heat conduction. However, this process disregards lateral-conduction error, so this paper analysis theoretically the error caused by lateral heat conduction due to temperature distribution on the surface. Also the results from one-dimensional plate hypothesis and the corrected results are compared and analyzed. When the non-dimensional excess temperature ranges between 0.44 and 0.55, and using narrow band TLC to measure the heat transfer coefficient on the disk between non-dimension radius of 0.77～0.94, the error due to lateral heat conduction would be controlled within 1.5%.

thermochromic liquid crystal; transient experiment; rotating cavity; lateral conduction;error

2017-01-21

国家自然科学基金资助项目(50806004)

王蕾(1988—)，女，助教，主要从事航空发动机涡轮部件的流动与传热方面研究，E-mail:495074022@qq.com。

王蕾,马庆辉,罗翔.基于一维假设的瞬态换热实验的误差修正[J].重庆理工大学学报(自然科学)，2017(11):94-101.

formatWANG Lei，MA Qinghui，LUO Xiang.Error Correction of Transient Heat Transfer Experiment Based on One Dimensional Hypothesis[J].Journal of Chongqing University of Technology(Natural Science)，2017(11):94-101.

10.3969/j.issn.1674-8425(z).2017.11.014

TK479+.22

A

1674-8425(2017)11-0094-08