巴基纸基复合材料导热性能模拟
2017-12-06张阿樱吕海宝
张阿樱, 吕海宝
(1.哈尔滨学院 图书馆, 黑龙江 哈尔滨 150086; 2.哈尔滨工业大学 复合材料与结构研究所, 黑龙江 哈尔滨150001)
巴基纸基复合材料导热性能模拟
张阿樱1,2, 吕海宝2
(1.哈尔滨学院 图书馆, 黑龙江 哈尔滨 150086; 2.哈尔滨工业大学 复合材料与结构研究所, 黑龙江 哈尔滨150001)
为了优化设计巴基纸/SMP复合材料的加热工况及巴基纸形状,本文采用有限元软件FLUENT分析了不同工况条件下正弦形及直线形巴基纸/SMP复合材料的热传导性能。研究结果表明:加热功率相同时,正弦形巴基纸/SMP复合材料的温度相对较低,温度分布均匀性较好。相同体积内热源作用下,正弦形巴基纸/SMP复合材料达到稳态时温度相对略高;但是正弦形及直线形巴基纸基复合材料达到稳态时,最高温度和最低温度的温差基本相同,远小于相同加热功率作用下正弦形及直线形巴基纸基复合材料达到稳态时最高温度和最低温度的温差。说明巴基纸基复合材料加热的均匀性主要取决于巴基纸加热片的单位体积内热源,而不是加热功率。分析认为,巴基纸加热片的单位体积内热源越小,巴基纸基复合材料达到稳态时温度越低,温度分布越均匀。
纳米复合材料; 温度分布; 有限元分析; 热学性能; 巴基纸
碳纳米管(carbon nanotubes,CNTs)被认为是终极的增强纤维,具有高长径比、低密度、高比表面积及优异的导电性能、力学性能、热学性能和化学稳定性等特点[1-3]。Yu等实验测量单壁碳纳米管(single-walledcarbon nanotubes, SWCNTs)的热导率值达到3 500 W/(m·K)[4],导热系数超过了金刚石和石墨。Fujii等采用实验方法对单根多壁碳纳米管热导率的测量值为2 000 W/(m·K)[5]。Hone等测量结果表明单根单壁碳纳米管的轴向热导率为1 800~6 000 W/(m·K)[6]。由纳米材料为增强相、以聚合物基体作为连续相制备的聚合物基纳米复合材料具有许多常规聚合物基复合材料无法比拟的优异的物理和化学性能。谢璠等研究表明:多壁碳纳米管(multi-walled carbon nanotubes, MWCNTs)的含量为2%时,多壁碳纳米管/环氧树脂基复合材料的热导率达到1.161 W/(m·K),复合材料的热导率比纯环氧树脂基体热导率提高了约6倍[7]。Zied等指出,碳纳米管质量百分含量为1%时,理论上计算纳米管/复合材料的导热率是纯聚合物基体导热率的10倍[8]。但是,当碳纳米管的掺量增大时,聚合物的粘度会增大,导致碳纳米管在聚合物基体中均匀分散难度也增大;并且由于CNTs在聚合物基体中有强烈的聚集倾向,因此纳米材料在复合材料中难以形成有效的网络通路。此外,碳纳米管具有化学惰性影响了其与聚合物基体间的相互作用和界面强度[9-11]。
由于将纳米材料和聚合物直接混合成型难以获得结构可控、性能优异的功能性纳米复合材料,研究人员提出一个较好的解决方法是采用碳纳米管及碳纳米纤维等纳米材料制作宏观形式上纸状物,即巴基纸(buckypaper, BP)[12-14]。将巴基纸作为增强相与聚合物基体复合制备出巴基纸/聚合物基复合材料[11,15],此方法能够有效克服碳纳米管在基体中分散不均匀及聚合物粘度增大等问题。巴基纸基复合材料在导电、防火、防雷击等领域具有广泛的应用前景。如能实现对巴基纸的有效控制,还可使其成为传感器及功能材料。由巴基纸与形状记忆聚合物(shape-memory polymer, SMP)制备的热敏性电致驱动纳米复合材料中,巴基纸通电后产生的电阻热传导至聚合物基体,当温度达到发生形状转变温度时,即触发了形状记忆效应,使巴基纸/形状记忆聚合物基复合材料实现电致驱动。此外,纳米复合材料广泛地应用于航空航天飞行器中,由于航空航天结构材料的工作环境复杂,导热性能成为影响纳米复合材料结构件性能的重要因素之一,因此对纳米复合材料在设计及制造过程中进行热学性能分析变得日益重要。
目前,关于巴基纸及其复合材料的力学性能和导电性能的研究相对较多,关于热学性能方面的研究则比较少,一些学者对聚合物基纳米复合材料的性能进行了建模研究[16-27],然而采用有限元软件FLUENT对巴基纸/SMP复合材料热学性能进行分析的极为少见。本文为了研究巴基纸加热片形状及单位体积内热源等因素对巴基纸/SMP复合材料达到稳态时温度分布的影响规律,采用有限元软件FLUENT分析了不同工况条件下正弦形及直线形巴基纸/SMP复合材料的热传导性能,为合理地设计巴基纸加热片形状控制、尺寸参数及加热工况提供理论依据。
1 建立模型
图1为直线形巴基纸加热片对聚合物基体的加热模型,L、T、w分别为聚合物基体的长度、厚度和宽度,d为巴基纸加热片的厚度。假设加热装置静置于空气中,散热方式为自然对流。接通电源后巴基纸加热片产生的热量使聚合物基体温度升高。通过自然对流散热,在一定时间后整个装置逐渐达到热稳定状态。

图1 加热试验装置示意图Fig.1 Images of heating experimental device
图2为采用的建模软件PROE 5.0建立的正弦形及直线形巴基纸/SMP复合材料的几何模型,模型中正弦形巴基纸加热片呈5个弯曲周期,每个弯曲周期为120 mm,即模型总长度为600 mm;正弦形巴基纸加热片的振幅为30 mm,模型总高度为100 mm,模型总宽度为50 mm。直线形巴基纸/SMP复合材料几何模型,模型长度、宽度及高度分别为600、50及100 mm。

图2 巴基纸基复合材料几何模型Fig.2 Geometric model of composites reinforced by buckypaper
巴基纸及SMP聚合物基体的参数如表1所示。

表1 巴基纸及聚合物基体参数Table 1 Parameters of buckypaper and polymer matrix
采用有限元软件FLUENT模拟巴基纸加热片对SMP聚合物基体加热过程的计算中,自然对流换热系数设为10 W/(m2·K),环境温度设为300 K;加热功率分别设为15、25、50 W,巴基纸厚度设为10 mm。
2 结果与讨论
采用有限元软件FLUENT分别分析了巴基纸加热片形状控制及单位体积内热源等因素对巴基纸基复合材料达到稳态时温度分布的影响规律。
2.1巴基纸加热片形状的影响
表2为巴基纸加热片的厚度为10 mm、加热功率为25 W的工况条件下,有限元软件FLUENT模拟分析的正弦形巴基纸/SMP复合材料及直线形巴基纸/SMP复合材料达到稳态时在z=0中心截面上典型温度分布。
表2不同形状巴基纸基复合材料在z=0截面的典型温度
Table2Typicaltemperatureofcompositesreinforcedbydifferentshapebuckypaperalongthesectionz=0
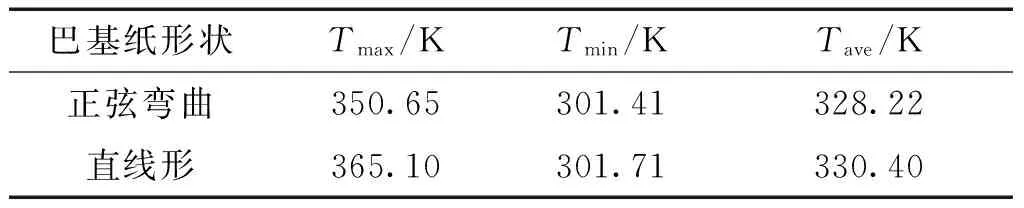
巴基纸形状Tmax/KTmin/KTave/K正弦弯曲350.65301.41328.22直线形365.10301.71330.40
如表2所示,正弦形巴基纸/SMP复合材料达到稳态时平均温度(Tave=328.22 K)、最高温度(Tmax=350.65 K)、最低温度(Tmin=301.41 K)均低于直线形巴基纸/SMP复合材料的平均温度(Tave=330.40 K)、最高温度(Tmax=365.10 K)、最低温度(Tmin=301.71 K)。计算结果表明:相同的加热功率作用下,与直线形巴基纸/SMP复合材料相比,正弦形巴基纸/SMP复合材料达到稳态时典型温度整体偏低。这是由于正弦形巴基纸加热片的长度相对较大,因此在相同加热功率作用下,正弦形巴基纸加热片的单位体积内热源较小,导致正弦形巴基纸基复合材料达到稳态时整体温度偏低。
图3、4分别为有限元软件FLUENT模拟分析的正弦形及直线形巴基纸/SMP复合材料达到稳态时在z=0中心截面及外表面的温度分布云图。由图3、4可知,与直线形巴基纸/SMP复合材料相比,正弦形巴基纸/SMP复合材料达到稳态时温度相对较低,且温度分布均匀性相对较好。由表2可知,正弦形巴基纸/SMP复合材料达到稳态时最高温度和最低温度的温差约为49 K,而直线形巴基纸/SMP复合材料达到稳态时最高温度和最低温度的温差约为63 K,最高温度和最低温度的温差可反映温度分布的均匀性。
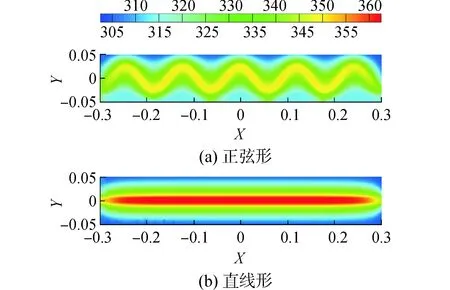
图3 不同形状巴基纸基复合材料在z=0截面温度分布云图Fig.3 Temperature cloudy map of nanocomposite reinforced by different shape buckypaper along the section z=0
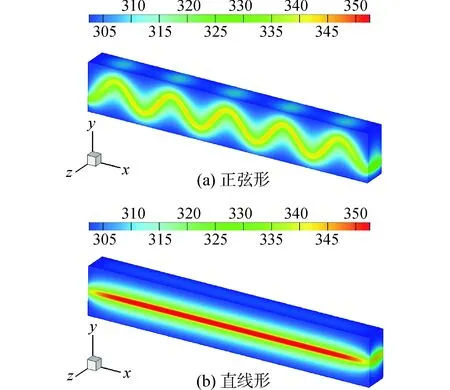
图4 不同形状巴基纸基复合材料在外表面温度分布云图Fig.4 Temperature cloudy map of nanocomposite reinforced by different shape buckypaper along the outer surface
分析结果表明,虽然直线形巴基纸/SMP复合材料达到稳态时温度相对较高,但是温度分布均匀性相对较差。此外,当巴基纸基复合材料温度分布不均匀时,复合材料内部会产生热应力,可导致其机械性能下降。因此可以根据实际需求是侧重要求温度还是力学性能来选择相应的巴基纸加热片的形状。
2.2单位体积内热源的影响
表3为巴基纸加热片的厚度为10 mm、单位为体积内热源为50 000 W/m3的工况条件下,有限元软件FLUENT模拟分析的正弦形巴基纸/SMP复合材料及直线形巴基纸/SMP复合材料达到稳态时在z=0中心截面上典型温度分布。从表3中可以看出,相同体积内热源作用下,和直线形巴基纸/SMP复合材料相比,正弦形巴基纸/SMP复合材料达到稳态时其最高温度(Tmax)、最低温度(Tmin)和平均温度(Tave)均相对略高。此外,由表3可知,正弦形巴基纸/SMP复合材料达到稳态时最高温度(Tmax=340.83 K)和最低温度(Tmin=301.14 K)的温差约为39 K,直线形巴基纸/SMP复合材料达到稳态时最高温度(Tmax=339.05 K) 和最低温度 (Tmin=300.94 K)的温差也约为39 K。远小于表2中相同加热功率(25 W)作用下正弦形及直线形巴基纸/SMP复合材料达到稳态时最高温度(Tmax)和最低温度(Tmin)的温差(分别为49 K和63 K)。说明加热的均匀性主要取决于巴基纸加热片的单位体积内热源,而不是加热功率。
表3不同形状巴基纸基复合材料在z=0截面典型温度
Table3Typicaltemperatureofnanocompositereinforcedbydifferentshapebuckypaperalongthesectionz=0
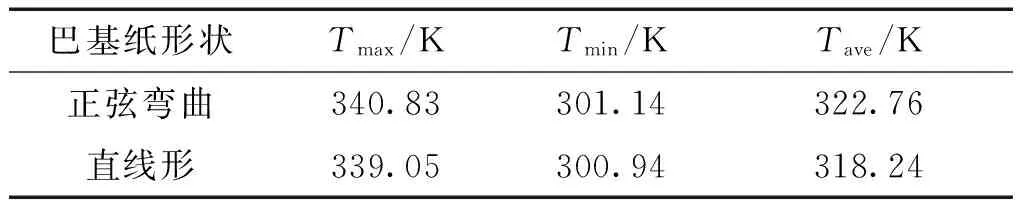
巴基纸形状Tmax/KTmin/KTave/K正弦弯曲340.83301.14322.76直线形339.05300.94318.24
图5为FLUENT模拟的相同体积内热源作用下,正弦形及直线形巴基纸/SMP复合材料达到稳态时在z=0截面的温度分布云图。

图5 相同单位体积内热源作用下不同形状巴基纸基复合材料在z=0截面温度云图Fig.5 Temperature cloudy map of nanocomposite reinforced by different shape buckypaper along the section z=0 under the same internal thermal source of unit volume
由图5可知,相同体积内热源作用下,正弦形及直线形巴基纸/SMP复合材料达到稳态时在z=0中心截面的温度分布较为均匀。
3 结论
1) 相同加热功率作用下,正弦形巴基纸/SMP复合材料达到稳态时最高温度、最低温度及平均温度相对较低,且温度分布均匀性较好。这是由于相同加热功率作用下,正弦形巴基纸加热片的单位体积内热源相对较小。
2) 相同体积内热源作用下,正弦形巴基纸/SMP复合材料达到稳态时典型温度相对略高;且正弦形及直线形巴基纸基复合材料达到稳态时最高温度和最低温度的温差基本相同,远小于相同加热功率作用下正弦形及直线形巴基纸基复合材料达到稳态时最高温度和最低温度的温差。说明巴基纸基复合材料加热的均匀性主要取决于巴基纸加热片的单位体积内热源,而不是加热功率。
[1] VALARCEL M, CARDENAS S, SIMONET B M. Role of carbon nanotubes in analytical science[J]. Analytical chemistry, 2007, 79(13): 4788-4797.
[2] IIJIMA S, ICHIHASHI T. Single-shell carbon nanotubes of 1-nm diameter[J]. Nature, 1993, 363(6430): 603-605.
[3] 安振河, 魏化震, 李莹, 等. 碳纳米管的分散及其对酚醛树脂热性能的影响 [J]. 工程塑料应用, 2006, 34(1): 19-23.
AN Zhenhe, WEI Huazhen, LI Ying, et al. Dispersion of CNTs and effect on heat performance of phenol-formaldehyde resin [J]. Engineering plastics application, 2006, 34(1): 19-23.
[4] POP E, MANN D, WANG Q, et al. Thermal conductance of an individual single-wall carbon nanotube above room temperature [J]. Nano letters, 2006, 6(1): 96-100.
[5] FUJII M, ZHANG X, XIE H, et al. Measuring the thermal conductivity of a single carbon nanotube [J]. Physical review letters, 2005, 95(6): 1-4.
[6] HONE J, WHITNEY M, ZETTL A. Thermal conductivity of Single-Walled Carbon Nanotubes [J]. Physical review B condensed matter, 1999, 103(s1-3): 2498-2499.
[7] 谢璠, 齐暑华, 李珺鹏,等. 聚合物基导热复合材料的研究进展 [J]. 中国胶粘剂, 2011, 20(9): 59-64.
XIE Fan,QI Shuhua,LI Junpeng,et al. Research progress of polymer-based composites with thermal conductivity [J]. China adhesives, 2011, 20(9): 59-64.
[8] ZIED A, FRANCOIS F J, GUILLAUME V. Eco-friendly conductive polymer nanocomposites (CPC) for solar absorbers design [J]. Polymers advanced technologies, 2013, 24(7): 638-645.
[9] CHANG C Y, PHILILIPS E M, LIANG R, et al. Alignment and properties of carbon nanotube buckypaper/liquid crystalline polymer composites [J]. Journal of applied polymer science, 2013, 128(3): 1360-1368.
[10] WANG Z, LIANG Z, WANG B, et al. Processing and property investigation of single-walled carbon nanotube (SWNT) buckypaper/epoxy resin matrix nanocomposites [J]. Composites part A applied science & manufacturing, 2004, 35(10): 1225-1232.
[11] GOU J, O'BRAIN S, GU H, et al. Damping augmentation of nanocomposites using carbon nanofiber paper [J]. Journal of nanomaterials, 2006, 2006(1): 189.
[12] VOHRER U, KOLARIC I, HAQUE M H, et al. Carbon nanotube sheets for the use as artificial muscles [J]. Carbon, 2004, 42(5/6): 1159-1164.
[13] HU L, HECHT D S, GRUNER G. Percolation in transparent and conducting carbon nanotube networks [J]. Nano letter, 2004, 4(12): 2513-2517.
[14] WANG C, ZHANG J, RYU K, et al. Wafer-scale fabrication of separated carbon nanotube thin-film transistors for display applications [J]. Nano letter, 2009, 9(12): 4285-4291.
[15] GOU J. Single-walled nanotube bucky paper and nanocomposites [J]. Polymer international, 2006, 55(11): 1283-1288.
[16] SWEETING R D, LIU X L. Measurement of thermal conductivity for fiber-reinforced composites [J]. Composites A, 2004, 35A(7-8): 933-938.
[17] ISLAM M R, PRAMILA A. Thermal conductivity of fiber reinforced composites by the FEM [J]. Journal of composite materials, 1999,33(18): 1699-1715.
[18] CAHILL D G, FORD W K, GOODSON K E, et al. Nanoscale thermal transport [J]. Journal of applied physics, 2003, 93(2): 793-818.
[19] ASCIOGLU B, ADANUR S, GUMUSEL L. Modeling of transverse direction thermal conductivity in micro-nano fiber-reinforced composites [J]. Textile research journal, 2009, 79(12): 1059-1066.
[20] CHEN G. Ballistic-diffusive equations for transient heat conduction from nano to macroscales [J]. Journal of heat transfer, 2002, 124(2): 320-328.
[21] YANG K, HE J, PUNEET P, et al. Tuning electrical and thermal connectivity in multiwalled carbon nanotube buckypaper [J]. Journal of physics condensed matter an institute of physics journal, 2010, 22(33):334215-334220.
[22] MEMON M O, HAILLOT S, LAFDI K. Carbon nanofiber based buckypaper used as a thermal interface material [J]. Carbon, 2011, 49(12): 3820-3828.
[23] HONG W T, TAI N H. Investigations on the thermal conductivity of composites reinforced with carbon nanotubes [J]. Diamond & related materials, 2008, 17(7): 1577-1581.
[24] GONNET P, LIANG Z Y, CHOI E S, et al. Thermal conductivity of magnetically aligned carbon nanotube buckypapers and nanocomposites [J]. Current applied physics, 2006, 6(1): 119-122.
[25] BIERCUK M, LLAGUNO M C, RADOSAVLJEVIC M, et al. Carbon nanotube composites for thermal management [J]. Applied physics letters, 2002, 80(15): 2767-2769.
[26] 吕海宝. 电驱动与溶液驱动形状记忆聚合物混合体系及其本构方程 [D]. 哈尔滨: 哈尔滨工业大学, 2010.
LYU Haibao. Electro-and solution-active shape memory polymer blends and their thermodynamic constitutive equation [D]. Harbin: Harbin Institute of Technology, 2010.
[27] 刘金世, 薛庆忠. 碳纳米管复合材料的有效热导率 [J]. 石油大学学报:自然科学版, 2004, 28(5): 142-144.
LIU Jinshi, XUE Qingzhong. Effective thermal conductivity of carbon nanotube composites [J]. Journal of the University of Petroleum, China: Nature Science Edition, 2004, 28(5): 142-144.
本文引用格式:
张阿樱, 吕海宝. 巴基纸基复合材料导热性能模拟[J]. 哈尔滨工程大学学报, 2017, 38(11): 1812-1816.
ZHANG Aying, LYU Haibao. Simulation analysis on thermal conductivity of composites reinforced by buckypaper[J]. Journal of Harbin Engineering University, 2017, 38(11): 1812-1816.
Simulationanalysisonthermalconductivityofcompositesreinforcedbybuckypaper
ZHANG Aying1,2, LYU Haibao2
(1.Library, Harbin University, Harbin 150086, China; 2.Center for Composite Materials and Structures, Harbin Institute of Technology, Harbin 150001, China)
To determine the optimum design shape of buckypaper and the heating conditions of Buckypaper/SMP composites, the finite element software FLUENT is used to analyze thermal conductivity of the composites reinforced by sinusoidal and line buckypaper under different working conditions. Results show that the temperature of the composites reinforced by sinusoidal buckypaper is lower than that with line buckypaper and that the temperature distribution is more even under the same heating power. Under the same internal heat source per unit volume, the temperature of the composites reinforced by sinusoidal buckypaper is higher when reaching the steady state, but the temperature difference between the highest and lowest temperatures is almost the same for the sinusoidal and line buckypaper when reaching the steady state, which is much lower than that determined under the same heating power. This result implies that the heating uniformity of the composites reinforced by buckypaper mainly depends on the heat source per unit volume of buckypaper heating sheets but does not depend on the heating power. Therefore, when the heat source per unit volume is small, the composites reinforced by buckypaper reach a steady state at a low temperature, and the temperature distribution is even.
nanocomposite; temperature distribution; finite element analysis; thermal properties; buckypaper
10.11990/jheu.201610001
http://www.cnki.net/kcms/detail/23.1390.u.20170428.1313.014.html
TB332
A
1006-7043(2017)11-1812-05
2016-10-01.
网络出版日期:2017-04-28.
黑龙江省博士后科研启动项目(LBH-Q16141);黑龙江省自然科学基金项目(E201454).
张阿樱(1973-), 女, 高级工程师, 博士后;
吕海宝(1979-), 男, 教授,博士生导师.
张阿樱, E-mail: zaying@sina.com.
