循环工况下变矩器叶片角设计空间的性能优化
2017-12-06李文嘉王安麟李晓田张庆武
李文嘉,王安麟,李晓田,张庆武
(1.同济大学 机械与能源工程学院,上海 201804; 2.山推工程机械股份有限公司,山东 济宁 272073)
循环工况下变矩器叶片角设计空间的性能优化
李文嘉1,王安麟1,李晓田1,张庆武2
(1.同济大学 机械与能源工程学院,上海 201804; 2.山推工程机械股份有限公司,山东 济宁 272073)
为解决整机循环工况与液力变矩器的匹配问题,并建立变矩器设计参数与整机工况的动力学映射关系,本文提出循环工况条件下变矩器叶片角设计空间的性能优化方法。该方法在整机物理实验条件下,以其变矩器的统计循环工况加权效率为评价目标,利用变矩器一元束流理论及其流固耦合仿真结果构建变矩器性能模型,对变矩器叶片角设计变量进行优化。优化过程中以整机V型和T型典型工况及双涡轮变矩器为研究对象,在变矩器流固耦合仿真精度得到台架实验验证的前提下,证明优化后变矩器统计循环工况加权效率分别提升2.64%和2.48%。该方法简易性地建立了整机与变矩器叶片角设计参数间的一体化动力学匹配关系,对同类面向主机的配件定制化设计具有工程化指导价值。
循环工况; 变矩器; 叶片角设计空间; 性能优化; 流固耦合仿真; 加权效率
液力变矩器因其启动扭矩大、载荷自适应能力强等特点广泛应用于工程机械。液力变矩器的传统设计方法仅考虑设计功率等粗糙设计指标和单一工况,不考虑整机循环工况,这导致变矩器与整机循环工况之间无法建立高效的动力学映射关系,制约变矩器实际作业时性能的提升。
为提升液力变矩器性能,学者做了大量研究:BANERJEE等建立变矩器关键参数对性能影响的敏感度方程,并优化出一组变矩器能量损失较小的结构参数[1],KESY等基于一元束流理论分析对变矩器性能产生主要影响作用的若干结构参数,并对其进行优化[2-3],WU等辅助计算机研究变矩器与发动机的匹配,以提高操作稳定性和舒适性[4];DI等在车辆减速条件下利用变矩器传动比等信息控制发动机扭矩[5];CUI等以动力性和经济性优化发动机与变矩器的匹配[6];王安麟等根据装载机循环工况提出变矩器性能匹配指标,但未对变矩器结构参数进行优化[7]。以上研究或单纯优化变矩器叶片结构,或单纯考虑变矩器与发动机的匹配,或考虑整机循环工况而未对变矩器进行性能优化,导致整机循环工况与液力变矩器的匹配问题存在较大研究空间。
为建立变矩器设计参数与整机工况的动力学映射关系,本文以5 t装载机用双涡轮液力变矩器为研究对象,根据装载机V型和T型典型工况的物理实验,统计循环工况条件下变矩器在各速比区间工作的概率,得到变矩器的统计循环工况加权效率计算公式,作为性能评价目标;在通过变矩器台架实验验证其流固耦合仿真精度基础上,利用流固耦合仿真结果修正变矩器一元束流理论中的经验系数,构建变矩器性能模型;对变矩器叶片角设计变量进行优化,并以流固耦合仿真验证性能优化方法的有效率性。
1 变矩器统计循环工况加权效率
工程机械具有作业循环性强、工况恶劣、工作载荷大等共同特点。本文以额定载重量为5 t的装载机用双涡轮液力变矩器(以下简称为变矩器)为对象,研究整机循环工况与变矩器的匹配问题。
1.1装载机循环工况实验
为保证变矩器速比区间分布的典型性,并验证“循环工况条件下变矩器叶片角设计空间的性能优化方法”的有效性,以装载机广泛应用的典型V型六段工况及T型六段工况作为实验循环工况。两种工况均包括了装载机实际作业的常用工况[8],由“空载前进接近物料”、“铲掘”、“满载倒退”、“满载前进”、“卸料”和“空载倒退”六个作业段组成,形成一个作业循环,是应用广泛的作业方式。具体实验方案如图1所示,在“空载前进接近物料”作业段,装载机在图示位置空载启动,铲斗浮动放平驶近料堆1~1.5 m处时下降动臂使铲斗接地,水平切入料堆;在“铲掘”作业段,铲斗以3°~7°的切削角插入料堆少许,加大发动机油门使铲斗全力切入料堆的同时,逐渐后倾并提升铲斗直至装满物料;在“满载倒退”作业段,铲斗装满物料,提升铲斗至运输高度(铲斗离地30~40 cm的高度),倒退至图示位置;在“满载前进”作业段,装载机满载驶向运输车辆;在“卸料”作业段,将铲斗举升至卸载高度,转动铲斗将其内物料倾卸;在“空载倒退”作业段,装载机空载倒档行驶离开运输车辆,回到原始位置,同时铲斗从高位放回低位,完成一个作业循环[9]。
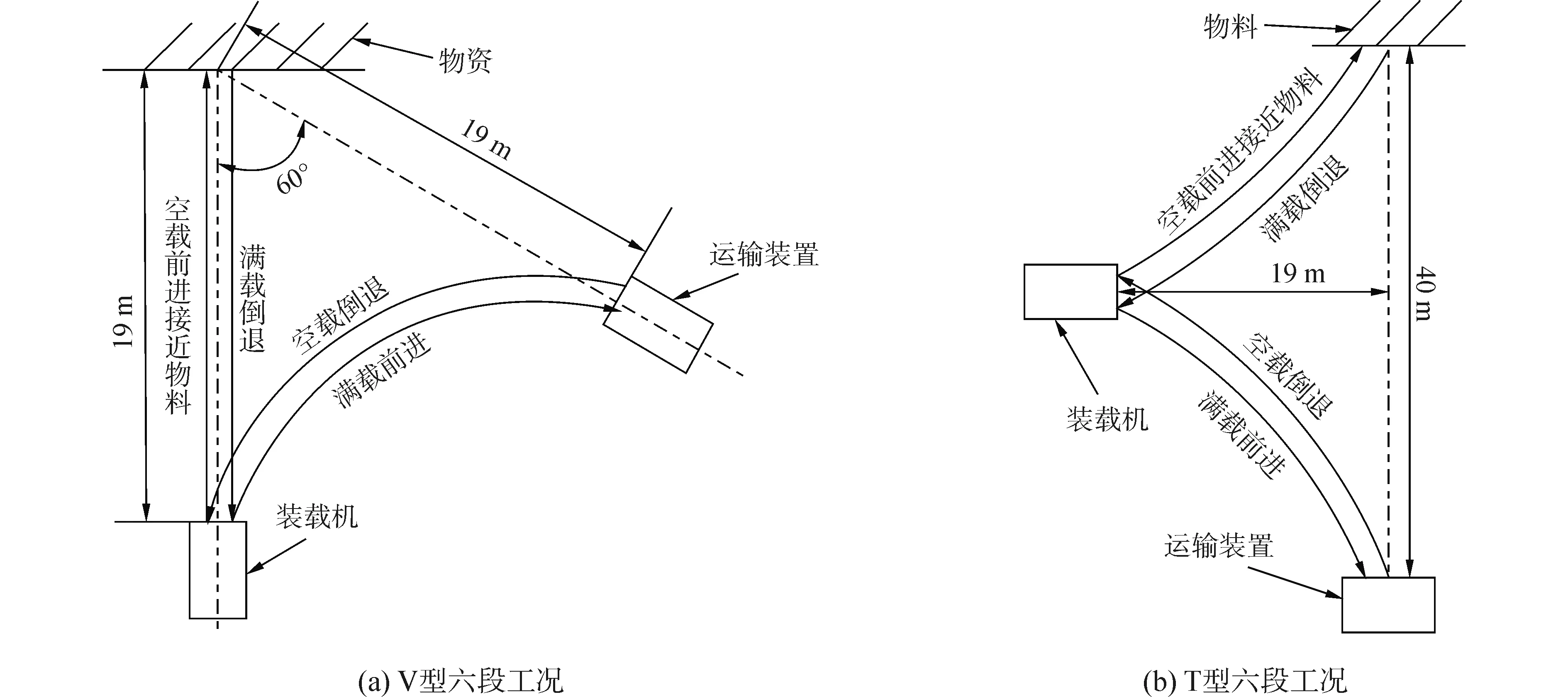
图1 装载机实验方案Fig.1 Experiment project of loader
实验条件:晴天,环境温度20 ℃,大气压为1.015 bar,大气相对湿度68%;作业对象为二类土(普通土);实验区间每段路况基本一致,实验车速稳定,循环实验时车辙保持一致;为消除实验驾驶员人为操作对测试结果的影响,采取由2名驾驶员各进行半数实验的方法。
这里需要指出:对于不同作业对象及工况,得到的变矩器统计循环工况加权效率会存在一定差异,变矩器的优化结果也会不同,由于无法针对所有作业对象及工况进行实验,因此仅以二类土为作业对象、选取V型和T型典型工况进行研究,以验证本文研究方法的有效性。
1.2变矩器的统计循环工况加权效率
对实验数据进行处理,分别得到两种工况下变矩器的速比[7],将变矩器的速比范围0~1分为10段,间隔0.1,统计得到循环工况条件下,变矩器在各速比区间的工作概率,如图2所示。
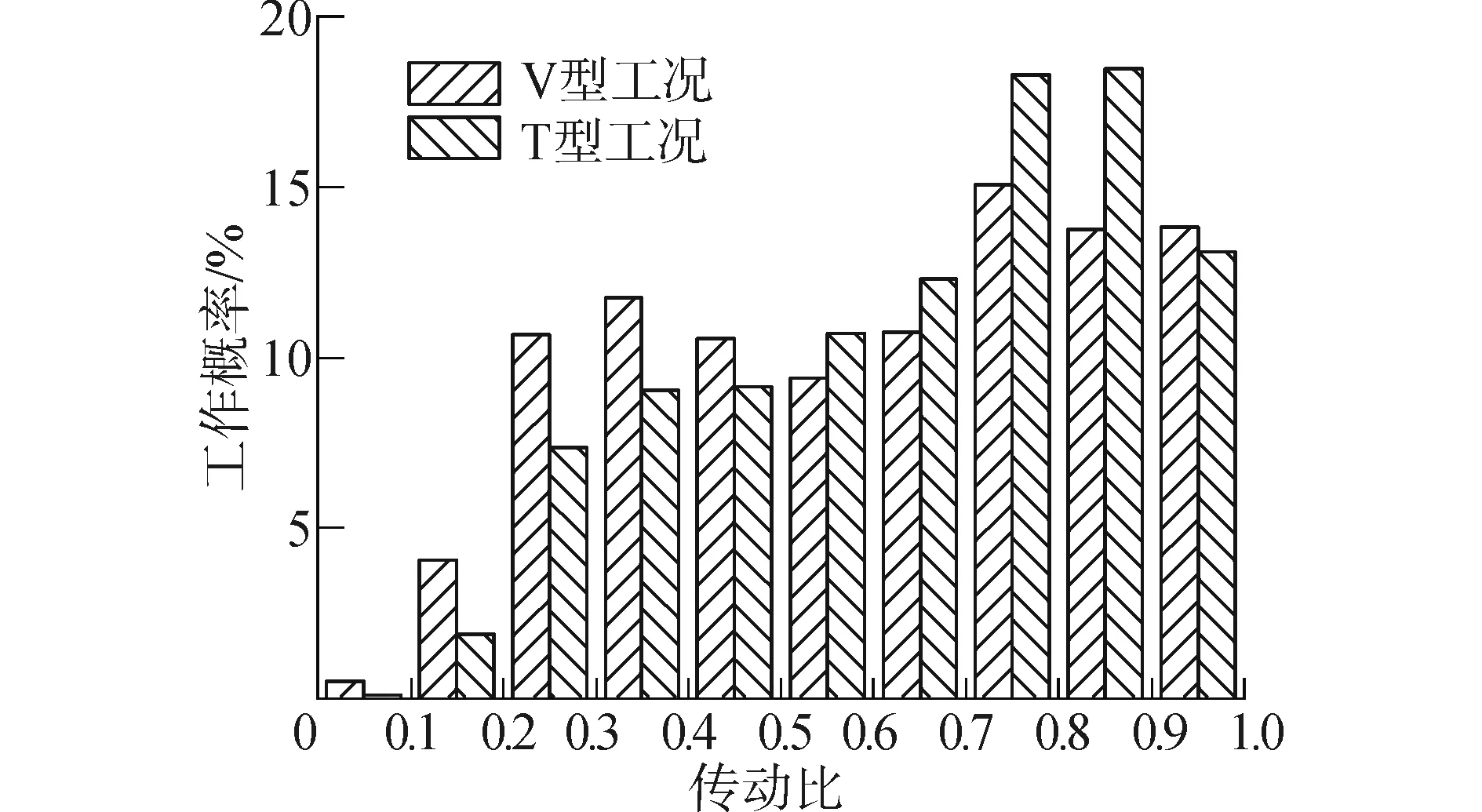
图2 变矩器在各速比区间的工作概率Fig.2 Working probability in each speed ratio interval
图2中某一速比区间对应的工作概率大,则表明变矩器更经常工作在此区间,变矩器在此区间的效率表现对变矩器实际工作时的效率影响更显著。从图2可以看出:V型工况下,变矩器更经常工作在传动比0.1~0.4,T型工况下,变矩器更经常工作在0.6~0.9。为定量化表征变矩器实际工作时的效率,以变矩器各速比区间对应的工作概率为权重,提出变矩器的统计循环工况加权效率(以下简称加权效率),其计算公式为
(1)
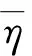
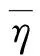
(2)
式中:η(k-1)/10+(m-1)/100表示速比为(k-1)/10+(m-1)/100时,变矩器的效率。将式(2)代入式(1),则可以得到变矩器加权效率公式:
(3)
变矩器加权效率基于整机循环工况得到,可以反映变矩器实际工作时的效率,因此将其作为变矩器评价目标。
2 叶片角设计空间的变矩器性能模型
2.1设计变量及建模方法
现有研究证明,变矩器叶片角对于变矩器性能的影响显著[1],因此选择变矩器叶片角作为变矩器设计变量。为保证性能模型的精度,每个设计变量取值范围是以现有变矩器产品叶片角为中心的±10°[10]。现有变矩器产品的叶片角及叶片角设计变量的取值范围如表1所示。
表1现有变矩器叶片角及设计变量的取值范围
Table1Bladeangleofcurrenttorqueconverterandvaluerangeofdesignvariables(°)
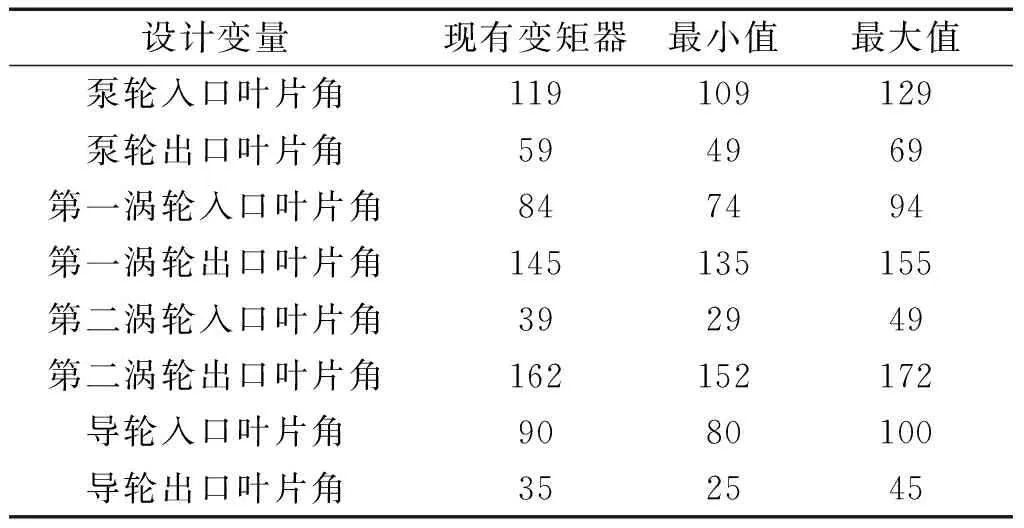
为便于对设计变量进行优化,性能模型需具有较快的计算速度,因此选用一元束流理论作为性能模型的建模理论。一元束流理论中的部分系数与变矩器型号和工况相关,如出口液流偏离和冲击损失系数。文献[11]以单涡轮液力变矩器为研究对象,根据流固耦合仿真结果求解了出口液流偏离和冲击损失系数,得到的模型对变矩器性能预测精度较高。本文采用相同的研究方法,即建立多组叶片角设计空间范围内的三维模型,分别对其进行流固耦合仿真,根据仿真结果求解变矩器的出口液流偏离和冲击损失系数。
2.2流固耦合仿真精度
流固耦合仿真技术可以方便地获得变矩器内部流场的信息,为本文研究出口偏离角和冲击损失系数提供了可能。流固耦合仿真对于变矩器的计算精度已经得到了学术界的证实[11-12],本文也进行了台架实验,并与其三维模型的流固耦合仿真进行了对比,如图3所示,转矩比、效率、泵轮能容的平均相对误差分别为0.86%、0.47%和1.02%,由此可知流固耦合仿真的误差较小。
2.3出口液流偏离
由于叶片的弯曲和叶轮的旋转,液体在叶轮流道内流动时并未完全贴合叶片,即出口液流与叶片之间存在一定偏离[12]。根据对于最高工况下的液流出口偏离,文献[12]给出了几种不同的经验公式,然而这些公式在其他效率下的计算精度较低。文献[11]假设叶片角变化不大的条件下,液流绝对速度的圆周分速度偏差仅与传动比相关,取得不错效果,因此本文采用相同假设。
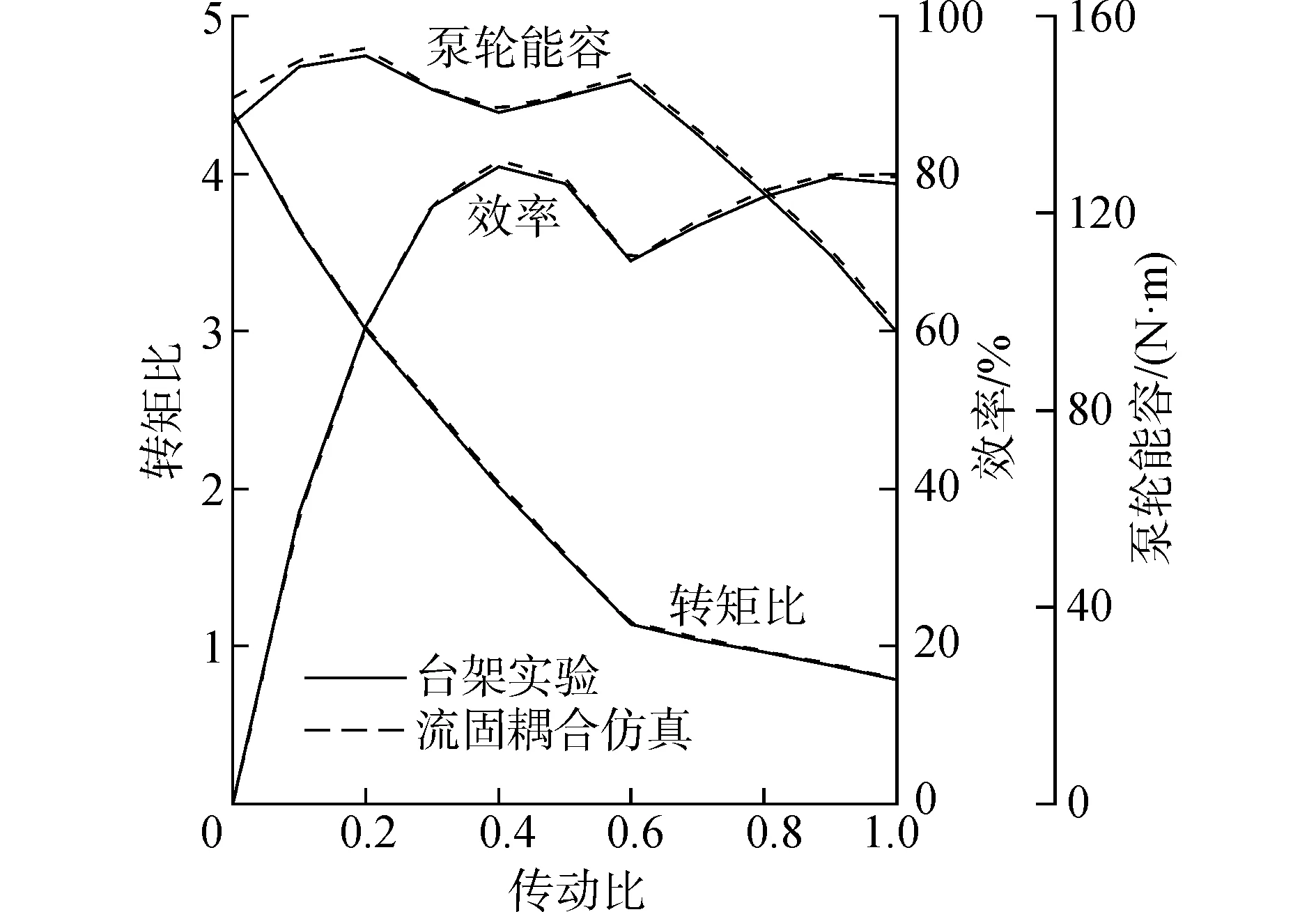
图3 台架实验与流固耦合仿真对比Fig. 3 Bench experiment and fluid-solid coupling simulation
根据流固耦合仿真结果及上述假设,可以得到4个叶轮液流绝对速度的圆周分速度偏差,如图4。
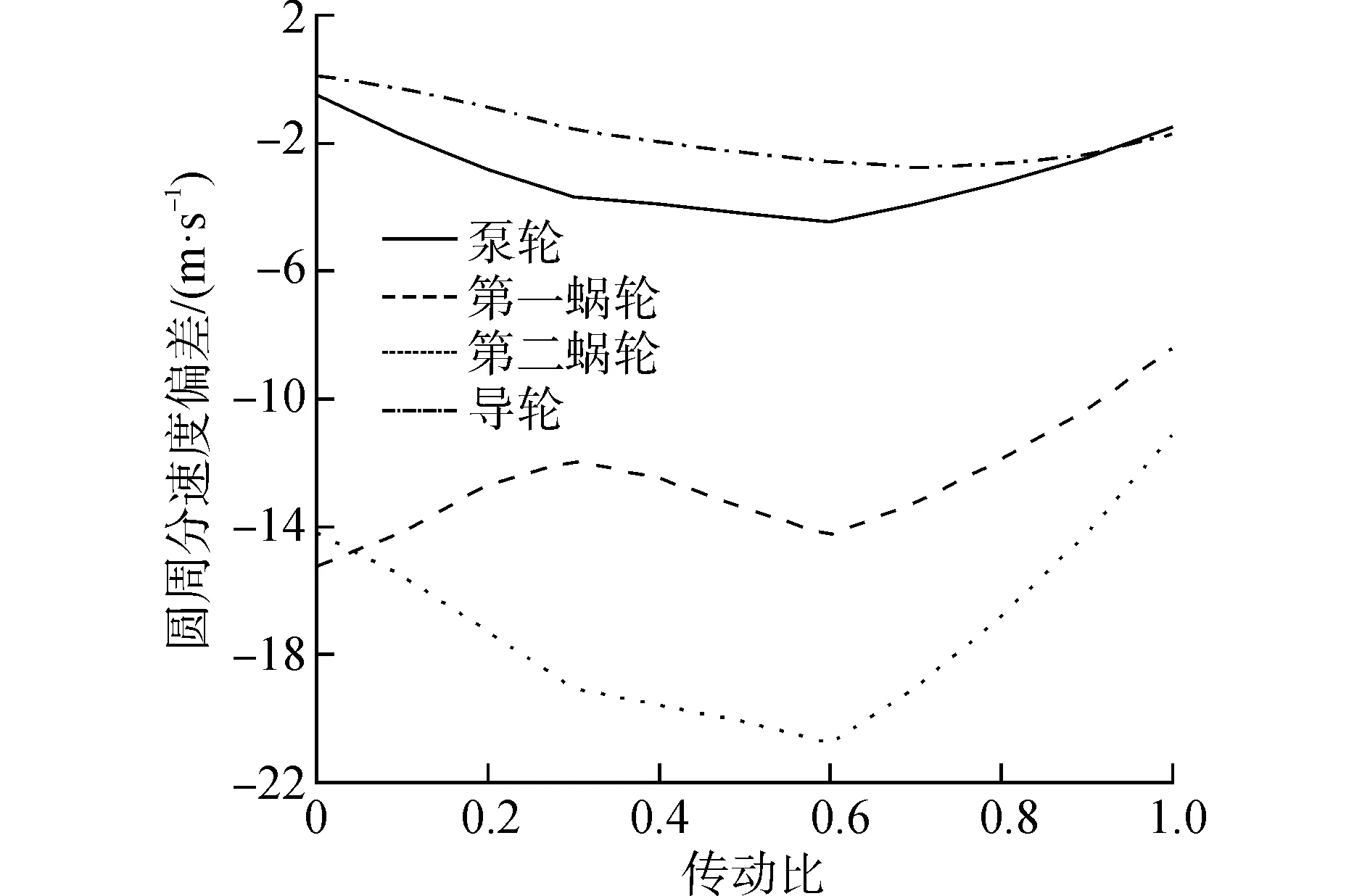
图4 液流绝对速度的圆周分速度偏差Fig.4 Peripheral velocity deviation of absolute velocity of flow
2.4冲击损失系数
一元束流理论利用冲击损失系数表征变矩器内部液体的能量损失。由于变矩器内部流场的复杂性,变矩器不同叶轮的冲击损失系数不同,同一叶轮的冲击损失系数在不同工况下也可能不同。现有的假设认为各叶轮的冲击损失系数由叶轮冲击工作面或非工作面决定,基于此假设的研究取得了不错的效果[11]。本文依照此假设,根据流固耦合仿真结果计算变矩器各叶轮的冲击角度及能量损失等相关物理量,根据冲击角度确定冲击工作面或非工作面,根据叶轮能量损失等物理量确定冲击损失系数。研究发现,由于泵轮转速较高且导轮静止,因此泵轮非工作面没有受到冲击。各叶轮的冲击损失系数如表2。
2.5性能模型精度的验证
确定出口偏离和冲击损失系数则可以完成性能模型的搭建。为验证性能模型的精度,在叶片角设计变量的取值范围内随机选取一组叶片角组合,根据此叶片角组合建模,并进行流固耦合仿真,与性能模型的预测进行对比,如图5所示。性能模型的平均偏差为1.5%。
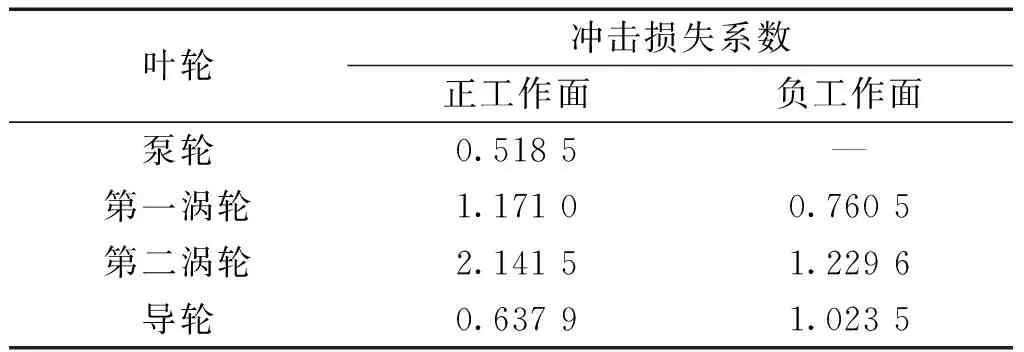
表2 各叶轮的冲击损失系数
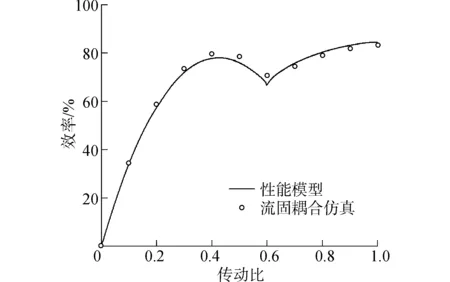
图5 性能模型与流固耦合仿真的效率对比Fig.5 Efficiency comparison of performance model and fluid-solid coupling simulation
3 循环工况条件下变矩器性能优化及验证
3.1变矩器性能优化结果
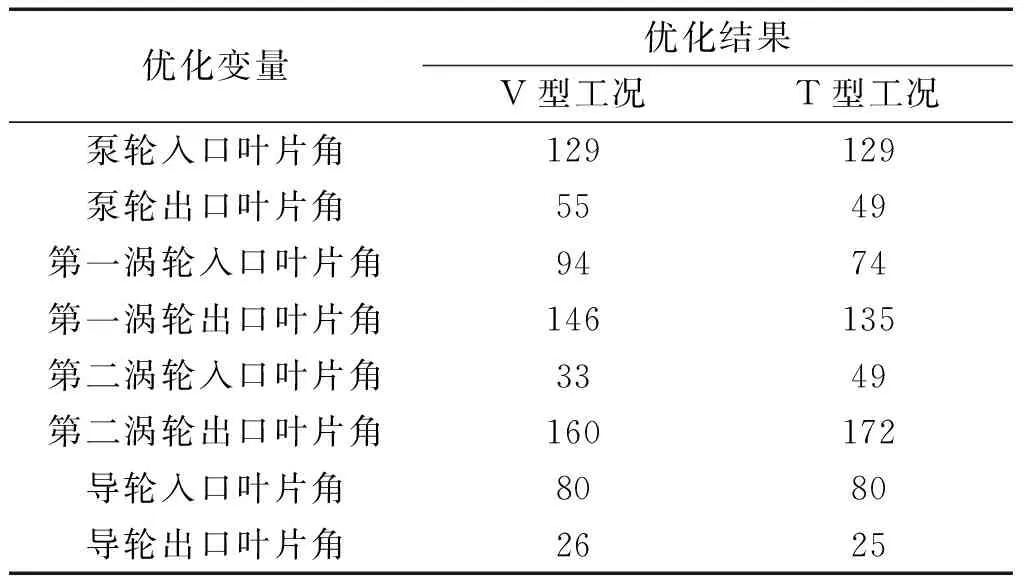
根据第2节建立的性能优化模型,在叶片角设计空间的范围内,以第1节推导的加权效率为优化目标,分别针对两种不同工况,对变矩器叶片角设计变量进行优化。优化结果如表3所示。
表3循环工况条件下变矩器叶片角优化结果
Table3Torqueconverterperformanceoptimizationresultsundertheconditionofdrivingcycle(°)
3.2性能优化结果的验证
根据表3所示的各叶轮叶片角可以建立变矩器三维模型,并进行流固耦合仿真。流固耦合仿真精度在2.2节进行了验证。两个优化模型与原始模型的流固耦合仿真的效率对比如图6所示。对于V型工况,V型工况优化模型、T型工况优化模型以及原始模型的加权效率分别为77.49%、77.23%和74.85%,V型工况优化模型的加权效率最高,且相对于原始模型提升2.64%;对于T型工况,三者的加权效率分别为78.24%、78.30%和75.82%,T型工况优化模型的加权效率最高,且相对于原始模型提升2.48%。
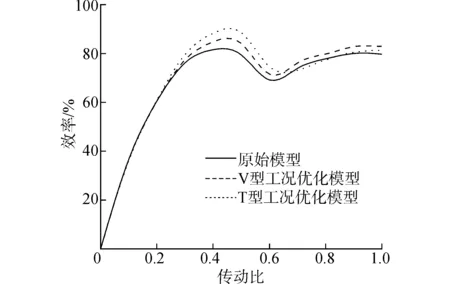
图6 优化模型与原始模型的效率对比Fig.6 Efficiency of optimization and original model
4 结论
1)根据流固耦合仿真分析,两个优化模型均在各自工况表现更高的加权效率;与原始模型相比,加权效率分别提升2.64%和2.48%。
2)该方法简易地建立了整机与变矩器叶片角设计参数间的一体化动力学匹配关系,对同类面向主机的配件定制化设计有工程化指导价值。
[1] BANEJEE J, ADIBI A H, LASHGARIAN A, et al. Parametric importance analysis and design optimization of a torque converter model using sensitivity information [J]. SAE international journal of passenger cars-mechanical systems, 2012, 5(1): 621-638.
[2] KESY A, KADZIELA. Constuction optimization of hydrodynamic torque converter with application of genetic algorithm [J]. Archives of civil and mechanical engineering,
2011, 6(4): 905-920.
[3] KESY A. Mathematical model of a hydrodynamic torque converter for vehicle power transmission system optimization [J]. International journal of vehicle design, 2012, 59(1): 1-22.
[4] WU H R, FENG L, ZHANG H S. Computer aided calculation of matching between engine and hydraulic torque converter [C]// Proceedings of the 2010 2nd International Conference on Future Computer and Communication, 2010: 6-9.
[5] DI C S, DOERING J, KOLMANOVSKY I V, et al. MPC-based control of engine deceleration with open torque converter [C]// 2012 IEEE 51st Annual Conference on Decision and Control, 2012: 3753-3758.
[6] CUI H W, WEI W, YAN Q D. Software development of steady numerical computational method of matching between hydrodynamic torque converter and engine [J]. Advanced materials research, 2011: 323-328.
[7] 王安麟,章明犬,李文嘉,等.采用装载机整机实验的液力变矩器性能匹配指标[J].西安交通大学学报, 2015, 10: 54-60.
WANG Anlin, ZHANG Mingquan, LI Wenjia, et al. Performance matching index of torque converter based on loader tests [J]. Journal of Xi′an Jiaotong University, 2015, 10: 54-60.
[8]王剑鹏. 50型装载机液压系统动态特性与热平衡研究[D]. 长春:吉林大学, 2011.
WANG Jianpeng. Study on dynamic characteristic and thermal balance of hydraulic system for 50-type loader [D]. Changchun:Jilin University, 2011.
[9] 徐礼超.装载机转向缸外负载力变化特性的试验研究[J]. 矿山机械, 2013, 42(11): 36-39.
XU Lichao. Test study on variation characteristics of external loading of steering cylinder in loader [J]. Mining & processing equipment, 2013, 42(11): 36-39.
[10] WILLI B. Stömungsmaschinen (Bere-chnung und Konstruktion) [M]. Vogel Press, West Germany, 1980.
[11] 吴光强,王立军. 基于CFD的液力变矩器等效参数性能预测模型[J]. 同济大学学报:自然科学版, 2013, 41 (1): 121-127.
WU Guangqiang, WANG Lijun. CFD analysis-based torque converter performance prediction model with equivalent parameters [J]. Journal of Tongji University: Natural Science, 2013, 41 (1): 121-127.
[12] 朱经昌.液力变矩器的设计与计算[M].北京:国防工业出版社, 1991.
本文引用格式:
李文嘉,王安麟,李晓田,等. 循环工况下变矩器叶片角设计空间的性能优化[J]. 哈尔滨工程大学学报, 2017, 38(11): 1781-1785.
LI Wenjia, WANG Anlin, LI Xiaotian, et al. Performance optimization of the design space of torque converter′s blade angle under the condition of driving cycle[J]. Journal of Harbin Engineering University, 2017, 38(11): 1781-1785.
Performanceoptimizationofthedesignspaceoftorqueconverter′sbladeangleundertheconditionofdrivingcycle
LI Wenjia1, WANG Anlin1, LI Xiaotian1, ZHANG Qingwu2
(1.School of Mechanical Engineering, Tongji University, Shanghai 201804, China; 2.Shantui Construction Machinery Co., Ltd., Ji′ning 272073, China)
To solve the matching problem between driving cycle and torque converter and to build the dynamics mapping relationship between the design parameters of torque converter and working condition, a performance optimization method for the design space of a torque converter′s blade angle under the condition of driving cycle was proposed. In a physical experiment, the statistics driving cycle weighted efficiency of the torque converter was taken as the evaluation objective. A performance model was built by using one-dimensional flow theory and the fluid-solid coupling simulation result of the torque converter. The blade angle design variables of the torque converter were optimized. Typical working conditions of V and T, and the torque converter with double turbines were the research object during the optimization. The statistics driving cycle weighted efficiency improved by 2.64% and 2.48%, respectively, as verified by the precision of the fluid-solid coupling simulation through a bench experiment on the torque converter. An integration dynamics mapping relationship between the whole machine and the blade angle design variables was established in a simple manner. The method has good engineering guidance value for the customized design of a machine with congeneric fittings.
driving cycle; torque converter; blade angle design space; performance optimization; fluid-solid coupling simulation; weighing efficiency
10.11990/jheu.201606058
http://www.cnki.net/kcms/detail/23.1390.u.20170427.1511.096.html
TH137.332
A
1006-7043(2017)11-1781-05
2016-06-20.
网络出版日期:2017-04-27.
2012年重大科技成果转化项目(〔2012〕258号).
李文嘉(1989-), 男, 博士研究生;
王安麟(1954-), 男, 教授, 博士生导师.
李文嘉,E-mail:pigeon_lwj_1989@126.com.
