竖直通道内降膜流动数值模拟研究
2017-12-06万智华厉彦忠陈宏振
万智华 厉彦忠 陈宏振
(1江苏建筑职业技术学院建筑设备与市政工程学院 徐州 221116;2西安交通大学能源与动力工程学院 西安 710049)
竖直通道内降膜流动数值模拟研究
万智华1,2厉彦忠2陈宏振1
(1江苏建筑职业技术学院建筑设备与市政工程学院 徐州 221116;2西安交通大学能源与动力工程学院 西安 710049)
降膜蒸发是一种高效的传热技术,平均液膜厚度是考察降膜蒸发传热性能的一个重要影响因素。本文基于VOF算法,建立了水和空气沿二维竖直通道降膜流动的CFD模型,模拟研究了液膜速度、工质种类、同向和逆向气流对平均液膜厚度的影响。结果表明:提高液膜速度会增大平均液膜厚度;气相工质对液膜厚度影响不大,而液相工质对液膜厚度影响较大,液膜厚度随液相黏度增大而增大;同向气流对入口段和发展段的液膜厚度影响不大,稳定段液膜厚度会随着同向气流速度的增大而减小;平均液膜厚度随逆向气流速度增大而降低,当逆向气流速度达到2.5 m/s后,气流速度对液膜厚度的影响减小。
两相流;降膜;波动;VOF算法;数值模拟
降膜流动具有传热温差小、换热效率高的优点,因此广泛应用于海水脱盐、食品工业、空调设备、化工等领域[1]。近些年,膜式主冷凝蒸发器在国外一些空分公司中得到了一定的应用。相关研究表明,液膜厚度是影响降膜传热传质的主要因素,当Re=30~1 600时,液膜表面会形成一定的表面波。当Re>167时,液膜开始出现孤立波,而波动会对液膜厚度产生一定影响,因此研究液膜波动的变化规律对分析液膜的传热传质性能十分关键[2-3]。传统研究降膜波动一般采用实验的方法[4-5]。实验方法数据比较可靠,但成本较高,有些物理量不便于测量。随着计算机模拟技术的发展,使数值模拟求解复杂的降膜流动成为了可能。VOF模型能够较好地捕捉气液两相界,因此在两相流模拟方面得到了较为广泛的应用。影响降膜流动的因素很多,如接触角、表面张力、工质物性、入口速度分布等。 J.K.Min等[6]采用 VOF模型模拟了竖直壁面下降膜的液膜厚度、波幅、波速和波动频率随雷诺数的变化。许松林等[7]模拟研究了气液速度和壁面切应力对液膜流型的影响。刘玉峰等[8]模拟了Re>4 760时竖壁下水降膜流动的情况。目前,对竖直壁面降膜已有一定的研究,但对不同气液工质种类、同向和逆向气流对液膜厚度影响的研究不多。本文模拟研究了液膜速度、工质种类、同向和逆向气流等因素对液膜厚度的影响,为降膜研究提供一定的理论基础。
1 模型与计算
1.1 物理模型与边界条件
建立了如图1所示的二维物理模型,流动长度为500 mm,宽度为 4.6 mm,液膜入口宽度为 0.6 mm。液相采用速度入口边界条件,壁面采用无滑移边界条件,其他均设为压力出口边界条件。为了更好地模拟壁面处的液膜波动情况,对近壁面处的网格进行了加密处理。

图1 物理模型Fig.1 Physical model
为防止网格数目对计算结果精度的影响,进行了网格无关性验证。计算了网格数量分别为14 500、30 000、60 000、120 000、150 000 个的 5 种网格模型。根据液膜的流动形态不同,许松林等[7]将流动方向划分为入口段、发展段和稳定段三个区域。本模拟中监测了流动方向L=150 mm,L=250 mm和L=350 mm三处液膜厚度的变化,并计算总平均液膜厚度δ—和液膜厚度相对偏差RET,不同网格模型下的计算结果如图2所示。当网格数目达到120 000时,继续增加网格数目时和RET变化不大。综合考虑计算精度和成本,最终采用网格数量为120 000的网格模型进行计算。
1.2 数学模型与计算方法
为了模拟液膜气液边界的变化,采用不可压缩非稳定求解设置和VOF模型。该模型引入了流体相体积分数α的定义,即各相体积分数之和等于1,如式(1)所示:

式中:αl、αg分别为液相、气相的体积分数。
各相体积分数方程如式(2)所示:


图2 网格无关性验证Fig.2 Verification of mesh independent
式中:αq为相体积分数,当q为l时,表示液相体积分数,当q为g时,表示气相体积分数;为速度矢量。
动量方程:
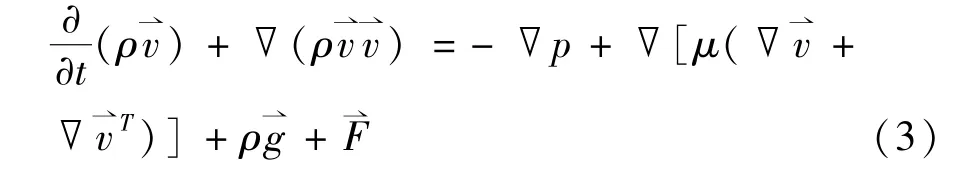
式中:p为压力,Pa;μ为动力黏度,kg/(m·s);ρ为密度,kg/m3;为重力加速度,m/s2;为体积力源项,kg/(m2·s2)。
式中:ρ和黏度μ的计算式分别为:

式中:ρl、ρg分别为液相、气相的密度,kg/m3;μl、μg分别为液相、气相的动力黏度,kg/(m·s)。
Fluent中连续表面张力模型(continuum surface force,CSF)是由 J.U.Brackbill等[9]提出的。 该模型提出的表面张力可以直接添加到动量方程的体积力源项F⇀中,如式(6)所示:

式中:σ为表面张力系数,N/m;κ为界面曲率,其计算式如下:

采用VOF模型,默认水和空气作为计算介质,第一相为空气,第二相为水。经计算Re<1 000,因此采用层流模型,压力和速度耦合采用PISO方法,动量方程采用二阶迎风差分格式。默认表面张力系数为0.072 N/m,默认接触角为45°。
1.3 模型验证
由于自由降膜通常存在着基底液膜、大的孤立波和小的毛细波,使液膜厚度并不固定,因此有必要采用统计方法来描述[10]。 Y.Q.Yu 等[11]指出统计变量主要分两种,一种是液膜厚度统计变量,包括平均液膜厚度、最大液膜厚度、最小液膜厚度和液膜厚度的标准差等;另一种是表面波统计变量,主要包括波频率、波长和波速等。
本文采用了平均液膜厚度来分析液膜厚度的变化,J.K.Min等[6]将各位置平均液膜厚度定义为瞬态液膜厚度的算术平均值,如式(8)所示,该定义可以反映各个位置液膜厚度的变化。

式中:δi为瞬态的液膜厚度,mm;n为样本的数目,本研究取流动时间为0.3 s,则样本数n=3 000。
同一工况3个位置处最大平均液膜厚度和最小平均液膜厚度的相对偏差定义为液膜厚度相对偏差RET,其计算式如(9)所示。该定义可以反映各个位置处液膜厚度的偏差。

为更好的对比不同工况下的结果,定义总平均液膜厚度为3个监测位置的平均液膜厚度的平均值,计算式为:
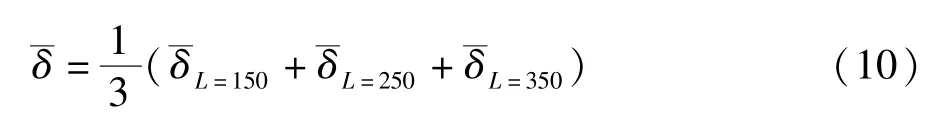
液膜Re定义式为:

W.Nusselt[12]提出层流降膜理论的平均液膜厚度计算式为:

式中:ν为液相运动黏度,m2/s。
A.E.Dukler等[13]采用全场速度分布计算出平均液膜厚度:

H.Brauer等[14-16]提出的平均液膜厚度计算式分别为:
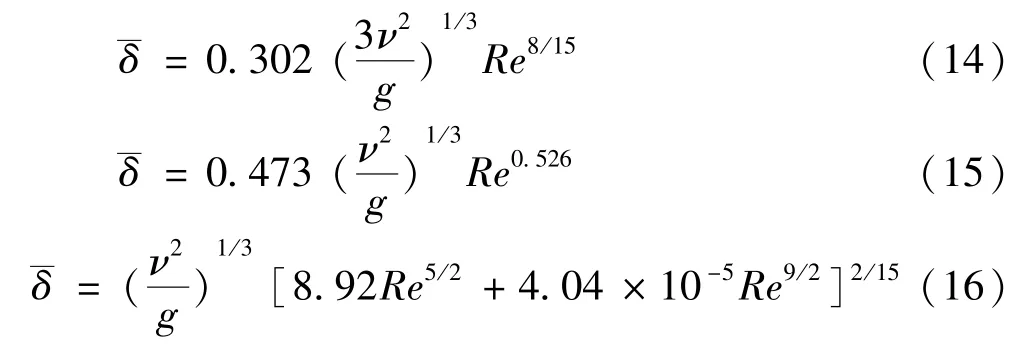
分别模拟了Re=200、649、1 000的3种工况,3个监测位置的平均液膜厚度结果如图3所示,为了使液膜厚度随雷诺数变化呈线性变化,横坐标采用了对数坐标。在相同Re工况下,不同位置的平均液膜厚度差异不大。通过与文献中的平均液膜厚度经验关联式对比,发现模拟结果和经验公式变化趋势吻合较好,结果与W.Nusselt[12]提出的经验公式最为接近。说明本文采用模型可以较为准确的模拟平均液膜厚度的变化。

图3 不同入口雷诺数下的平均液膜厚度Fig.3 Average film thickness()for different Re
图4给出了流动方向L=0.35~0.40 m位置的气相分布云图,x为液膜的厚度,m。图中显示下降液膜存在类似的正弦波,具有较为陡峭的波前和平缓的波背,这与 D.Gao等[17]的结果吻合。
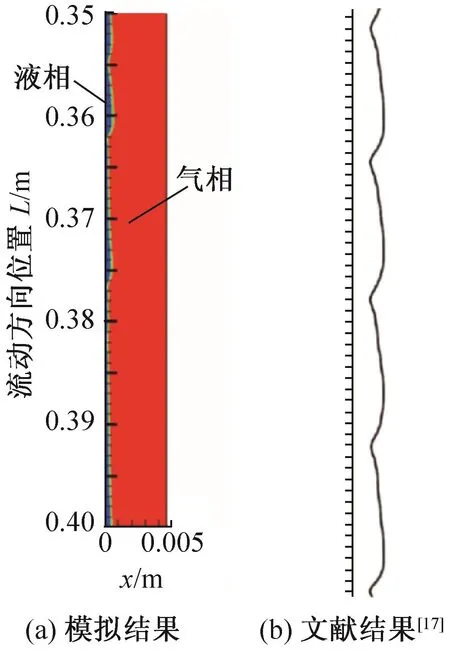
图4 正弦波状图Fig.4 Figure of sinusoidal⁃type wave
为进一步验证模型的可靠性,对流动方向L=0.365 ~0.380 m 范围内某个孤立波(如图 5)内的速度进行分析。
为了与文献中液膜速度对比,横坐标采用液膜厚度与最大液膜厚度之比x/δmax,纵坐标采用液膜速度和最大液膜速度之比u/umax,绘制如图6所示的流动方向上L=0.375 m处液膜速度随厚度方向的变化,模拟结果与 W.Nusselt等[18-20]结果吻合较好,进一步验证了模型的可靠性。
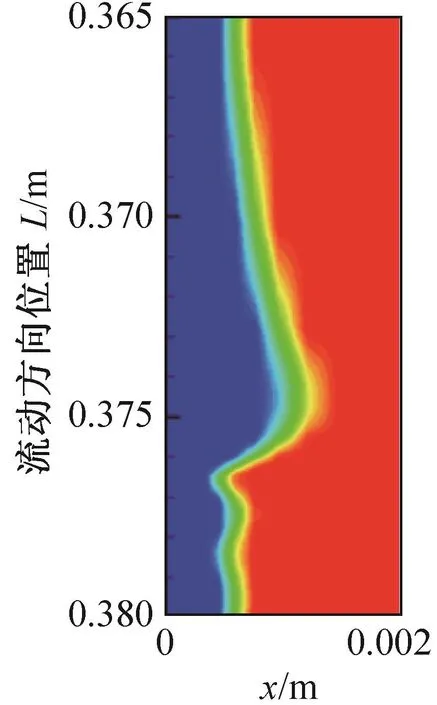
图5 孤立波图Fig.5 Figure of the solitary wave
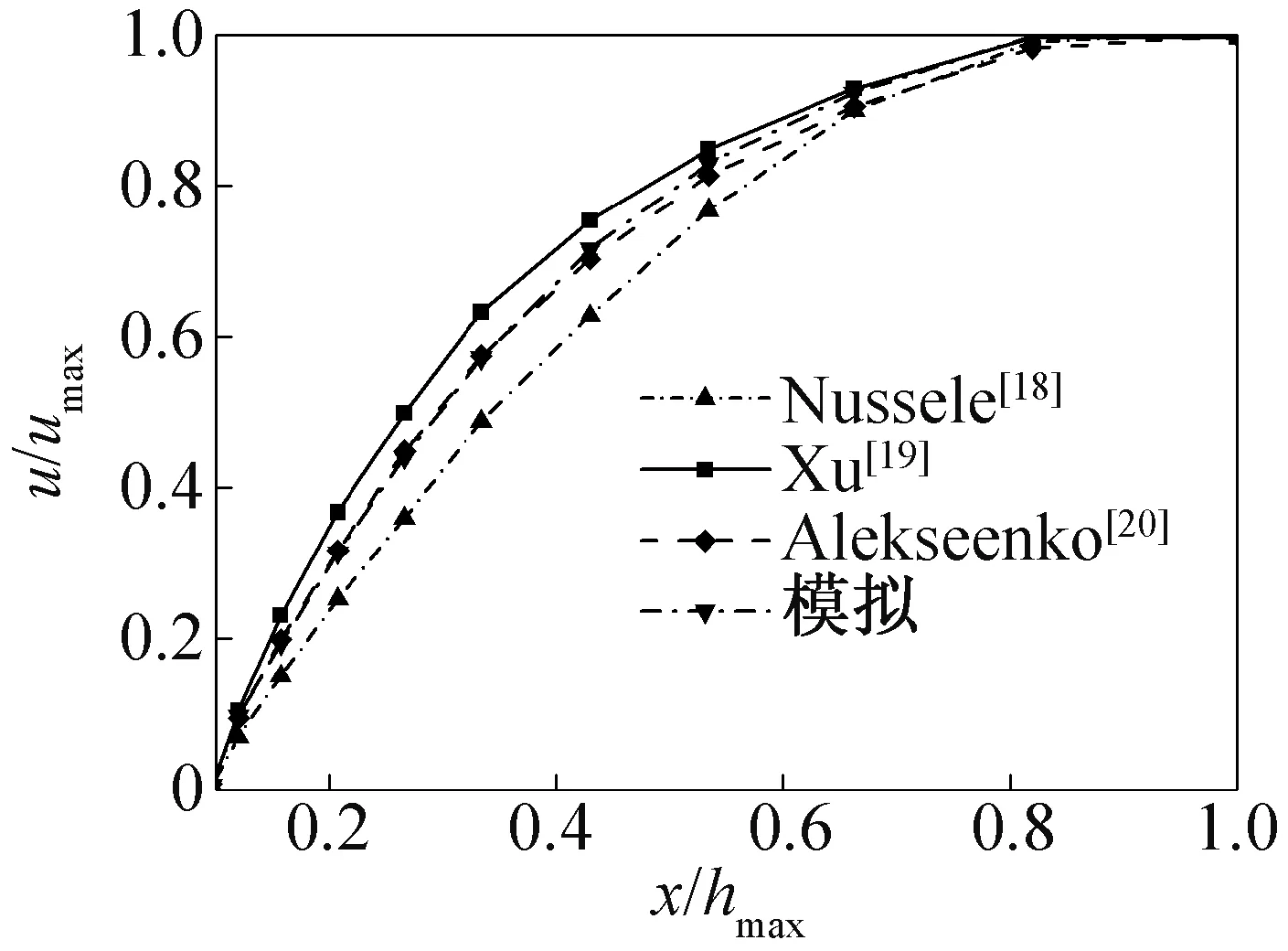
图6 液膜速度随厚度变化Fig.6 Velocity varies with film thickness
2 模拟结果与分析
2.1 液膜速度的影响
为了使得模拟结果更加准确,采用 W.Nus⁃selt[18]理论入口速度分布作为液膜入口的边界条件,如式(17)所示。为了研究不同入口速度u0的影响,本文研究了6种速度条件下的情况,入口速度u0分别为 0.33、0.59、0.84、1.09、1.42、1.67 m/s。 总平均液膜厚度如图7所示,随液膜入口速度的增大而呈增大趋势。这主要是因为液膜流量增加,使液膜厚度出现相应的增大,说明液相雷诺数Re越大,平均液膜厚度越大。
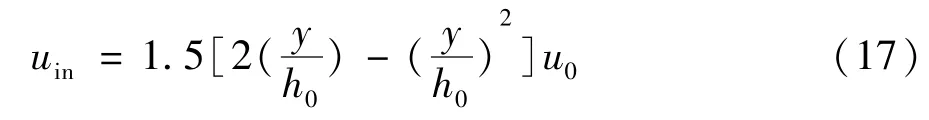
式中:uin为入口液膜速度,m/s;h0为入口液膜厚度,mm,取h0=0.6 mm;u0为液膜平均速度,m/s;y为液膜的距离壁面的距离,m。
2.2 工质种类的影响
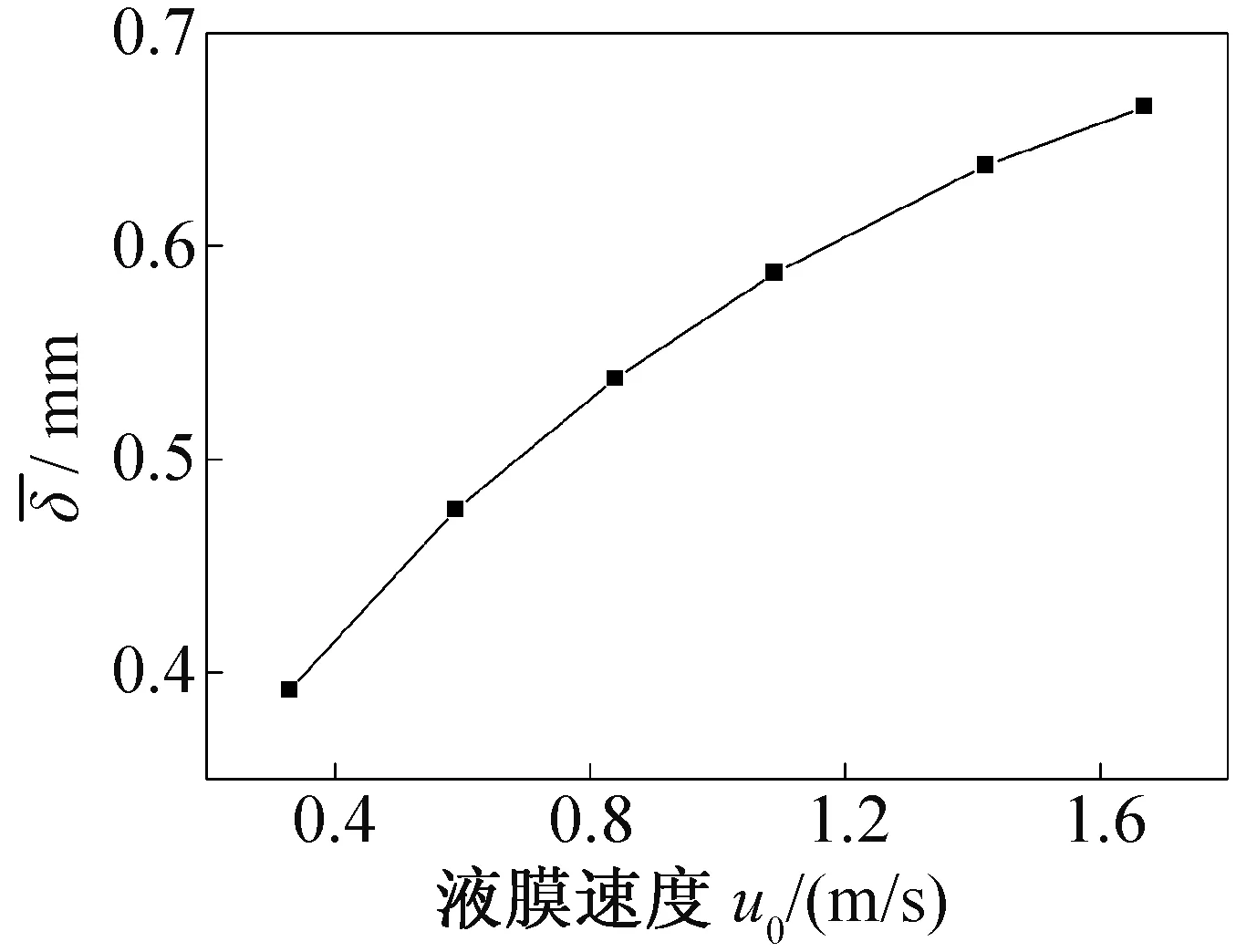
图7 总平均液膜厚度随入口液膜速度变化Fig.7varies with film velocity
为研究不同工质降膜厚度的分布情况,本文研究了6种气液工质对下的工况,工质物性参数如表1所示。所有工况的入口液相速度均为0.335 m/s。经模拟,总平均液膜厚度如图8所示。可以明显看出,当液相确定时,改变气相种类对平均液膜厚度几乎没有影响,而液相种类影响较大。在所有工况中,以乙醇、水、甲苯为液相工质的总平均液膜厚度依次减小。经计算,以甲苯为液相的液膜Re=297,以乙醇为液相的液膜Re=132,得到结果却是后者液膜厚度更大,说明平均液膜厚度不仅与雷诺数有关,还与液相黏度有关。这是因为黏度越大,越容易黏滞在壁面上,导致液膜厚度增加。 由式(12)、式(14) ~(16)可以看出,液膜的平均厚度与工质的黏度呈现正相关的关系,说明模拟结果和文献中提出的平均液膜厚度经验关联式结果吻合较好,进一步验证了模型的可靠性。
2.3 同向气流的影响
由于降膜蒸发过程中会源源不断地产生气体,气体的存在会影响液膜的流动,进而导致液膜厚度变化。因此,有必要研究气流对平均液膜厚度的影响。研究了4种同向气流速度工况,气相入口速度分别为1.0、1.5、2.0、2.5 m/s,以气相入口设置为压力出口条件的工况为参考工况,各位置平均液膜厚度δ—随不同工况的变化如图9所示,给出了各个位置的平均液膜厚度的标准差。同向气流对流动入口段和发展段的总平均液膜厚度影响不大。随着流动的不断发展和同向气流的不断增大,液膜发展段的平均液膜厚度出现下降趋势。当速度为2.5 m/s时,L=350 mm平均液膜厚度降为最低,相比压力出口的工况减少了3.8%。图中的纵向图线上下端的横线位置代表的是液膜厚度的标准差,长度越长,表示液膜厚度的标准差越大,液膜波动越明显。不难看出,随着气流速度的增大,三个位置的平均液膜厚度标准差逐渐增大,说明随着同向气流速度的增大,平均液膜厚度的波动程度增大。
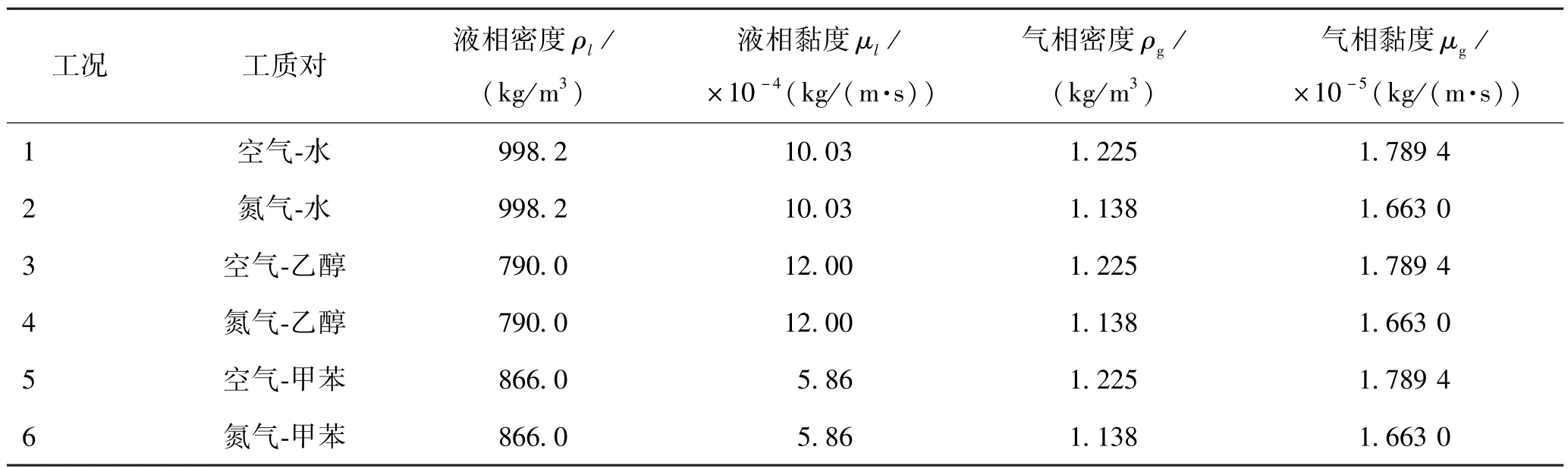
表1 不同工质对物性Tab.1 Material properties for different medium groups
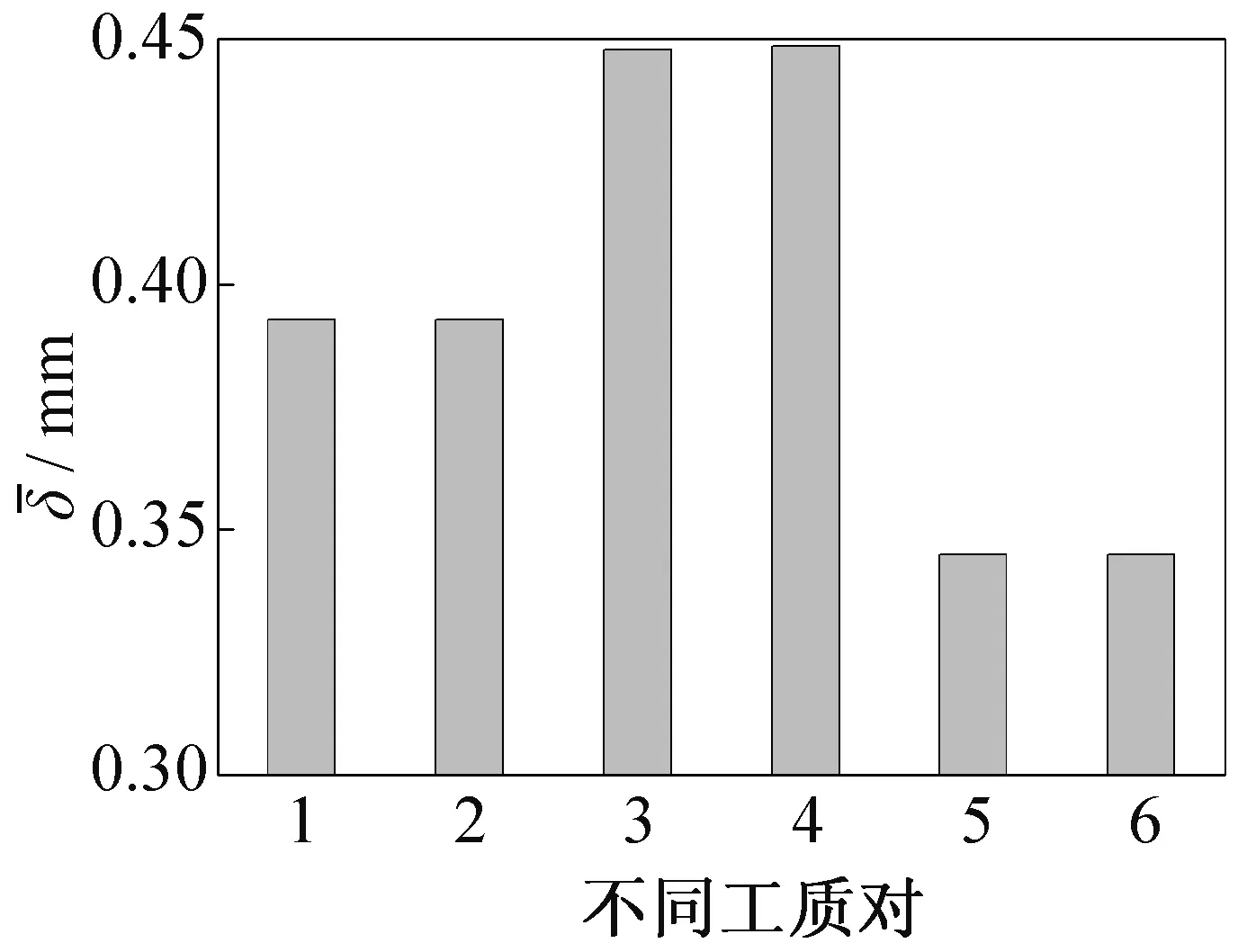
图8 不同工质对下平均液膜厚度Fig.8for different medium groups
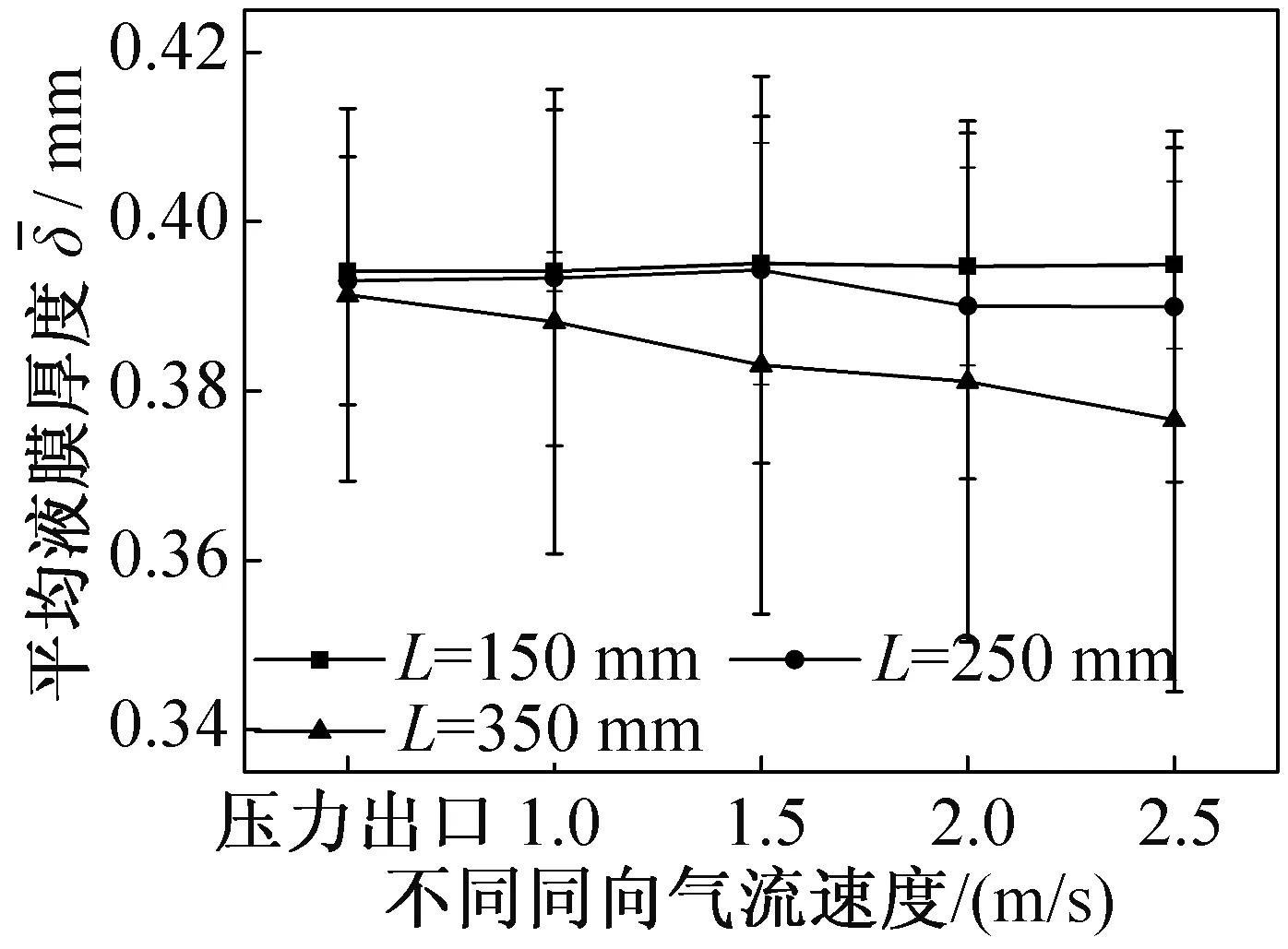
图9 各位置平均液膜厚度随同向气流速度变化Fig.9 Average film thickness()varyies with co⁃current gas velocity
图10为不同同向气流速度下整个通道内的气相分布云图。以没有同向气流的工况为参考工况,发现液膜上面的孤立波之间距离较近。孤立波之间的基底液膜厚度较厚。随着同向气流的增大,孤立波波峰之间的间距不断增大,且基底液膜厚度逐渐变薄,特别是在液膜流动后期,这一现象更加明显。这主要是由于气流的扰动作用迫使液膜的波峰出现偏移,增加了液膜的流动速度,使液膜更加快速的流出通道,导致液膜厚度降低。没有同向气流时,在流动方向L=0.2 m以后才出现波动,但随着气相速度的不断增大,在流动方向0.2 m之前也出现了液膜波动现象,这是由于气体的剪应力改变了表面波的涡旋结构、尺度及个数,导致液膜表面波出现变化,与于意奇[21]提出的结果相符。
2.4 逆向气流的影响
为了研究逆向气流对液膜厚度的影响,研究了4种不同逆向气流的速度工况,气相速度入口分别为 -1.0、-1.5、-2.0、-2.5 m/s,并与压力出口的参考工况结果进行对比。由于在逆向气流工况下,不同位置处液膜厚度基本相等,因此只给出总平均液膜厚度δ—随不同逆向气流工况的变化,结果如图11所示。随着逆向气流速度的不断增大,总平均液膜厚度出现降低的趋势。当逆向气相速度达到2.5 m/s之后,逆向气相速度对液膜厚度的影响趋于平缓。同时,总平均液膜厚度的标准差出现增大趋势,说明随着逆向气体速度增大,会导致液膜厚度出现较大的波动,这是由逆向气体产生的剪应力导致的结果。
图12所示为不同逆向气流工况下液膜速度随液膜厚度x方向的变化,随着逆向气流的增大,液膜内的速度呈逐渐减小的趋势。这是由于逆向气相出口靠近液相的入口,会对液相产生反向的切应力,减少了液膜的流入速度,导致液膜厚度的降低。
3 结论
降膜蒸发是一种高效的传热技术。液膜沿着壁面向下流动是一个波动的过程,波动对于液膜的厚度影响很大,而液膜厚度的大小是影响液膜导热的一个重要因素。因此,了解液膜厚度的变化规律是研究液膜传热传质的基础。本文通过数值模拟的方法研究了入口速度、不同工质、同向气流和逆向气流对平均液膜厚度的影响。主要得到结论如下:

图10 不同同向气相流速下的气相分布云图Fig.10 Gas distributions for different co⁃current gas velocity

图11 不同逆向气流速度下总平均液膜厚度Fig.11for different counter⁃current gas velocity

图12 不同逆向气流下液膜速度随厚度方向变化Fig.12 Film velocity varies with thickness for different counter⁃current gas velocity
1)当采用Nusselt入口速度分布作为液膜入口速度时,增加液膜入口的速度会导致平均液膜厚度增大,说明液相雷诺数越大,平均液膜厚度越大。
2)当入口液膜速度相同时,对于不同工质对,液相工质种类相同时,改变气相工质种类对平均液膜厚度影响不大。平均液膜厚度不仅与液膜雷诺数有关,还与液相黏度有关,黏度越大,液膜厚度越大。
3)当入口液膜速度恒定,且存在同向气流时,增加气流速度使液膜稳定段的平均液膜厚度出现降低的趋势,而液膜入口段和发展段变化并不明显。当存在逆向气流时,增加气流速度会导致流动方向各位置的平均液膜厚度出现降低的趋势。而当逆向气相速度达到2.5 m/s后,继续增大速度对液膜厚度影响程度降低。
本文受江苏建筑职业技术学院校级课题项目(JYA315⁃13),江苏省住房和城乡建设厅项目(2016ZD56),江苏建筑职业技术学院品牌专业建设项目(PPZY2016A01)资助。(The project was supported by the university project of Jiangsu Voca⁃tional Institute of Architectural Technology (No.JYA315⁃13),Department of Housing and Urban⁃Rural Development of Jiangsu Province (No.2016ZD56).),Brand Profession project of Jiangsu Vocational Institute of Architectural Technology (No.PPZY⁃2016A01).)
[1]万智华,厉彦忠,周媛媛.低温流体在竖直通道中降膜蒸发研究进展[J].制冷学报,2016,37(5):112⁃118.(WAN Zhihua,LI Yanzhong,ZHOU Yuanyuan.Research progress of falling film evaporation of cryogenic fluid in ver⁃tical channels[J].Journal of Refrigeration,2016,37(5):112⁃118.)
[2]PARK I S,MAN Y K.Numerical investigation of the heat and mass transfer in a vertical tube evaporator with the three⁃zone analysis[J].International Journal of Heat &Mass Transfer,2009,52(1/2):2599⁃2606.
[3]YU Y Q,WEI S J,YANG Y H,et al.Experimental study of water film falling and spreading on a large vertical plate[J].Progress in Nuclear Energy,2012,54(1):22⁃28.
[4]YU Y Q,CHENG X.Experimental study of water film flow on large vertical and inclined flat plate[J].Progress in Nu⁃clear Energy,2014,77:176⁃186.
[5]SIEBENECK K,POPOV W,STEFANAK T,et al.Pillow plate heat exchangers⁃investigation of flow characteristics and wetting behavior at single⁃flow conditions[J].Chemie Ingenieur Technik,2015,87(3): 235⁃243.
[6]MIN J K,PARK I S.Numerical study for laminar wavy motions of liquid film flow on vertical wall[J].Internation⁃al Journal of Heat & Mass Transfer,2011,54(15/16):3256⁃3266.
[7]许松林,赵婵.气液并流垂直液膜流动的数值模拟[J].天津大学学报 (自然科学与工程技术版),2014,47(12):1039⁃1046.(XU Songlin,ZHAO Chan.Numeri⁃cal simulation of co⁃current gas⁃liquid vertical liquid film flow[J].Journal of Tianjin University (Science and Tech⁃nology),2014,47(12):1039⁃1046.)
[8]刘玉峰,童一峻,任海刚,等.高雷诺数竖壁降膜流动特性的数值研究[J].红外技术,2010,32(10):567⁃571.(LIU Yufeng,TONG Yijun,REN Haigang,et al.Numerical investigation on flow characteristics of falling wa⁃ter film down a vertical plate at high reynolds number[J].Infrared Technology,2010,32(10):567⁃571.)
[9]BRACKBILL J U,KOTHE D B,ZEMACH C.A continu⁃um method for modeling surface tension[J].Journal of Computational Physics,1992,100(2):335⁃354.
[10]吴正人,宋朝匣,刘梅,等.流动液膜的数值模拟研究综述[J].化工进展,2015,34(9):3216⁃3220,3255.(WU Zhengren,SONG Zhaoxia,LIU Mei,et al.Review on the numerical simulation of the flowing liquid film [J].Chemical Industry and Engineering Progress,2015,34(9):3216⁃3220,3255.)
[11]YU Y Q,CHENG X.Experimental study of water film flow on large vertical and inclined flat plate[J].Progress in Nu⁃clear Energy,2014,77:176⁃186.
[12]NUSSELT W.Der waè rmeaustausch am berieselungskuè hler[J].VDI⁃Z,1923,67(9):206⁃216.
[13]DUKLER A E,BERGELIN O P.Characteristics of flow in falling liquid films[J].Chemical Engineering Progress,1952,48(11):557⁃563.
[14]BRAUER H.Strömung und wärmeübergang bei rieselfil⁃men[J].VDI⁃Forschungsheft,1956,457(22): 1⁃40.
[15]TAKAHAMA H,KATO S.Longitudinal flow characteris⁃tics of vertically falling liquid films without concurrent gas flow[J].International Journal of Multiphase Flow,1980,6(3):203⁃215.
[16]ARAGAKI T,TOYAMA S,SALAH H M,et al.Transi⁃tional zone in falling liquid film [J].Kagaku Kõgaku Ronbunshū,1987,13(3):373⁃375.
[17]GAO D,MORLEY N B,DHIR V.Numerical simulation of wavy falling film flow using VOF method[J].Journal of Computational Physics,2003,192(2):624⁃642.
[18]NUSSELT W.Die oberflachen kondensation des wasser⁃damfes[J].Zeitsehrit des Vereines Deutscher Ingenieure,1916,60:569⁃575.
[19]XU Z F,KHOO B C,WIJEYSUNDERA N E.Mass trans⁃fer across the falling film: simulations and experiments[J].Chemical Engineering Science,2008,63(9):2559⁃2575.
[20]ALEKSEENKO S V,YE N V,POKUSAEV B G.Wave formation on a vertical falling liquid film[J].Aiche Jour⁃nal,1985,31(9):1446⁃1460.
[21]于意奇.大尺度平板水膜流动行为的数值模拟和试验研究[D].上海:上海交通大学,2012.(YU Yiqi.Ex⁃perimental and numerical study on film flow behavior on la⁃ger scale flat plate[D].Shanghai: Shanghai Jiao Tong Uni⁃versity,2012.)
Numerical Simulation of Falling Film Flow in Vertical Channel
Wan Zhihua1,2Li Yanzhong2Chen Hongzhen1
(1.School of Construction Equipment and Municipal Engineering,Jiangsu Vocational Institute of Architectural Tech⁃nology,Xuzhou,221116,China;2.School of Energy and Power Engineering,Xi′an Jiaotong University,Xi′an,710049,China)
Falling⁃film evaporation is an efficient heat⁃transfer technology.The average film thickness is an important factor that affects the heat⁃transfer performance.Based on the volume of fluid (VOF) algorithm,a computational fluid dynamics (CFD) model was estab⁃lished to describe the flow of a two⁃phase (air⁃water) falling film on a two⁃dimensional vertical channel.The effects of the film velocity,working medium,and co⁃current and counter⁃current gas on the liquid film thickness were investigated.The results show that the film thickness grows with the increasing film velocity.The gas⁃phase medium has little effect on the liquid⁃film thickness;however,the liquid medium has a great influence,and the film thickness increases with the liquid⁃film viscosity.The co⁃current gas flow has little effect on the film thickness in the entry and development regions.However,in the stable regions,the film thickness decreases with the increasing co⁃current gas velocity.The average film thickness decreases with the increase of the counter⁃current gas velocity.When the counter⁃cur⁃rent gas velocity reaches 2.5 m/s,the gas⁃velocity′s influence on the liquid⁃film thickness decreases.
two⁃phase flow;falling film;fluctuation;VOF algorithm;numerical simulation
Li Yanzhong,male,Ph.D,professor,School of Energy and Power Engineering,Xi′an Jiaotong University,+ 86 29⁃82668738,E⁃mail:yzli⁃epe@ mail.xjtu.edu.cn.Research fields:cycle of re⁃frigeration and cryogenic system and process of thermal physical,research for the law of flow and heat transfer of cryogenic fluid.
TB657.5;TK124;TQ051.6
A
0253-4339(2017)06-0080-07
10.3969 /j.issn.0253 - 4339.2017.06.080
2017年4月17日
厉彦忠,男,博士,教授,西安交通大学能源与动力工程学院,(029) 82668738,E⁃mail: yzli⁃epe@ mail.xjtu.edu.cn。 研究方向:制冷与低温系统循环及热物理过程、低温流体流动与传热规律。
