基于位置修正的轨迹测量方法研究
2017-12-06崔莅杭陈贵金王勇刚
崔莅杭,陈贵金,王勇刚
(湖北三江航天红峰控制有限公司,湖北 孝感 432000)
基于位置修正的轨迹测量方法研究
崔莅杭,陈贵金,王勇刚
(湖北三江航天红峰控制有限公司,湖北 孝感 432000)
传统精密轨迹测量方法大都采用GPS、全站仪等设备,存在设备不易架设、数据不连续、对环境要求较高等缺点。针对该问题提出一种基于航位推算系统的轨迹测量方法。该方法在航位推算基础上引入了位置修正技术,通过起始点与终点坐标即可计算出系统俯仰角误差、方位角误差及里程仪标度因数误差。系统完成航位推算计算后,用求解出的系统误差对航位推算轨迹进行修正,即可获得高精度的轨迹数据。最后通过试验验证该方法可行,系统行进153m误差小于0.12m。
轨迹测量;惯性导航;航位推算;位置修正
0 引言
精密轨迹测量对确保大型工程(如桥梁、隧道等)的顺利实施、工程的优质、日常运营状况的安全检测等有着重大意义。目前国内实施重大工程项目的测量仪器普遍使用GPS接收机、全站仪、精密水准仪等,在隧道内还部分使用陀螺定向仪、激光指向仪等检测设备[1-4]。这种测量方法存在着众多局限性:基准点不易确定,测量设备不易架设等难点;只能进行多点测量,不能提供连续的测试数据;环境要求较高,测量过程中GPS无信号或视线被遮挡等状况会影响测量精度。针对传统方法的不足,文献[5-6]提出了采用光纤陀螺进行轨迹测量的方法,但该方法只能进行二维数据测量,使用场合受到限制。文献[7-8]提出利用惯性导航系统进行轨迹测量的方法,虽然惯性导航系统能够进行三维测量,但是其误差随时间累积,单纯的惯性导航系统无法满足测量的精度需求。
里程仪是用来测量载体行驶速度和距离的仪器,可以利用里程仪和惯性导航系统组成航位推算系统对惯性导航系统的误差进行抑制。本文研究了一种基于航位推算系统的轨迹测量方法。首先,对航位推算误差进行了分析,之后针对航位推算误差引入了位置修正技术,最后通过推行实验对该方法进行了验证。
1 航位推算误差分析

航位推算是陆用系统常用的导航定位方法,陀螺进行姿态、方位解算,里程仪计算位移增量,其误差模型已经比较成熟[9],这里直接引用:
式中:
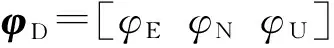
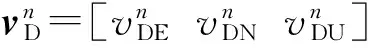
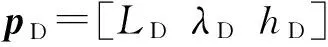
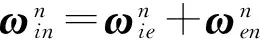
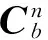

KD为里程仪标度因数;

其中,RM与RN分别为子午圈曲率半径与卯酉圈曲率半径。
在实际测量操作中,系统由人工推行因此车速不会高于2m/s;其次,推行路程较短,轨迹误差小于10m。因此忽略高阶小量,式(1)可简化为
(2)
通过式(2)可以看出,对航位推算系统位置误差影响最大的因素为系统姿态误差角φD与里程仪标度因数误差δKD。
如果能够对φD和δKD进行修正,将可以提高航位推算系统的精度。
2 位置修正
位置修正技术基于航位推算的相似性原理[10],利用载体起点、终点坐标以及航位推算解算出的坐标可以计算出姿态误差角φD以及里程仪标度因数误差δKD。由于系统运行较短,因此认为在运行过程中各误差量不变。
φD包括两种误差:对准误差ΦD与m系相对于b系的安装误差αD。其中横滚安装偏差角αDY对定位误差没有影响[6],而对准水平姿态误差比较小(小于0.02°),因此可以不对横滚引起的位置误差进行修正。
2.1 方位误差角估计
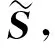
(3)
方程左侧为两边与夹角之积,右侧为向量叉乘第三分量。方位误差角由式(3)可以求出

(4)

图1 方位误差估计原理图Fig.1 The scheme of azimuth estimation
2.2 里程仪标度因数估计
根据相似性原理,不论载体如何运行,最终计算位移与实际位移之比均为常值1+δKD,所以有
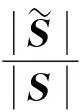
(5)
2.3 俯仰误差角估计
由式(2)分析可知,高度位置误差为航位推算计算的行驶路程在高程方向投影产生,而产生投影的原因为存在俯仰误差角。因此有公式
(6)

则俯仰误差角为

(7)
航位推算计算路程可由b系下的里程仪输出累计求得。
3 轨迹测量算法
通过A、B两点坐标采用式(4)、式(5)、式(7)分别计算出角度误差φDZ、φDX及里程仪标度因数误差δKD,利用3个估计误差对航位推算轨迹进行修正。
在实际工程中,轨迹测量一般使用全站仪坐标系进行数据处理。该坐标系定义如下:
1)坐标原点为起点;
2)从起点向终点在水平面内的投影引直线,该直线方向定义为X轴,指向终点方向为正向;
3)垂直于水平面为Z轴,朝天为正;
4)Y轴与其他两轴成右手定则。
采用全站仪坐标系后,原点坐标P0=[0 0 0],其后坐标均为相对于P0点的位移,因此修正公式如下

(8)
式中:
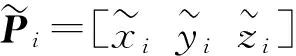
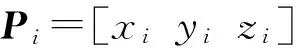
为修正矩阵。
4 试验验证
4.1 试验准备
为验证文中轨迹测量方法,采用实际系统进行相关试验。惯性导航系统安装于试验小车上,车轮上装有里程仪,车体上装有指针用于进行路标点对点,验证用系统相关参数如下:
1) 陀螺零漂≤0.15(°)/h;
2) 加计零偏≤0.2mg;
3) 里程仪标度因数为1.7×10-4m/p。
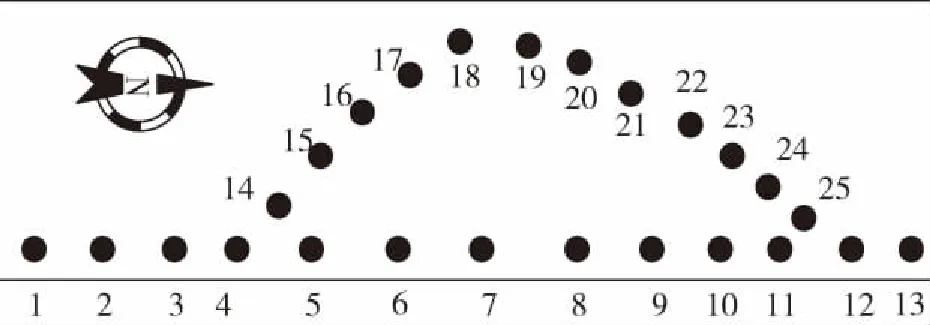
图2 路线图Fig.2 Route map
试验场地选择在车辆较少的公路上,试验前规划好行车路线。在行车路线上每隔十几米设置路标点,用于考察系统精度,如图2所示,其中1点与13点直线距离为153.07m。所有路标点采用全站仪测量水平位置及高程,全站仪精度优于0.01m。试验采用人工推行方式,行进平均速度约为1m/s,推行过程中指针会经过所标记的路标点,指针经过路标点时通过软件进行打标,方便事后进行精度对比。
试验选择两条路线,路线规划如表1所示,每条路线推行4次。

表1 试验路线规划
4.2 试验结果
两条线路试验数据见表2~表5。
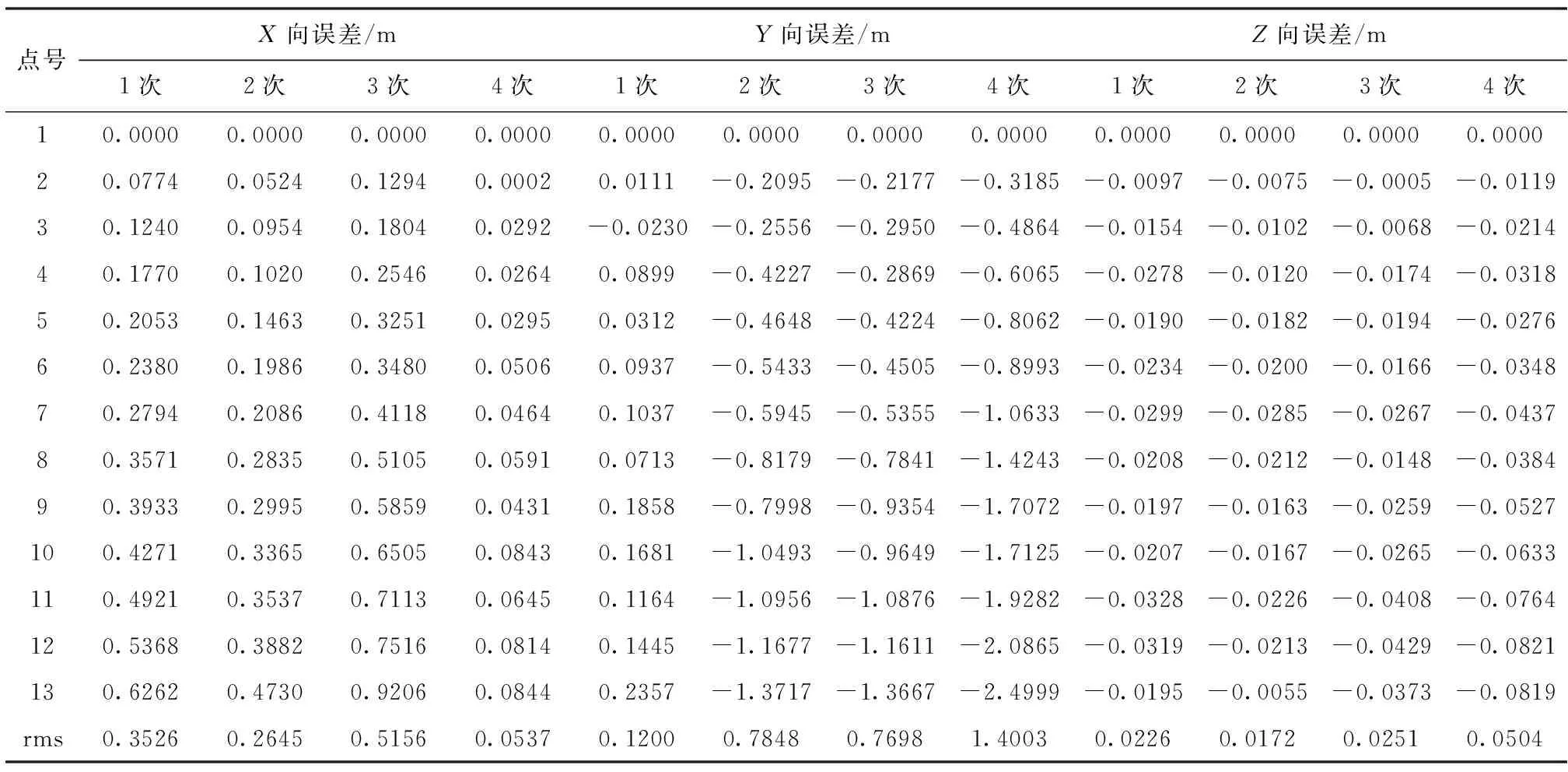
表2 第一条路线航位推算数据

表3 第一条路线位置修正后数据

表4 第二条路线航位推算数据

表5 第二条路线位置修正后数据
通过试验数据可以看出,两次试验单独采用航位推算时X向最大误差为0.94m,Y向最大误差为2.69m,Z向最大误差为0.1m。采用本文方法修正后,X向最大误差为0.051m,Y向最大误差为0.1175m,Z向最大误差为0.0696m。
图3~图4所示为第一条路线第一组试验轨迹图。从图3中可以看出,直接采用航位推算进行测量时,由于存在方位误差角,水平最大误差,X向为0.63m,Y向为0.24m。而图4表明高程上由于俯仰误差角的影响最大误差为0.0328m。采用本文方法修正后,X向最大误差为0.03m,Y向最大误差为0.07m,高程最大误差为0.026m。

图3 平面轨迹图Fig.3 Plane trajectory

图4 高程轨迹图Fig.4 Altitude trajectory
图5~图6所示为第二条线路第二组试验轨迹图。从图5中可以看出,直接采用航位推算进行测量时,X向为0.3m,Y向为0.5m。而图6表明高程上最大误差为0.1m。采用本文方法修正后,X向最大误差为0.04m,Y向最大误差为0.12m,高程最大误差为0.07m。
修正前后轨迹对比表明采用位置修正可以提高航位推算轨迹的精度。

图5 平面轨迹图Fig.5 Plane trajectory
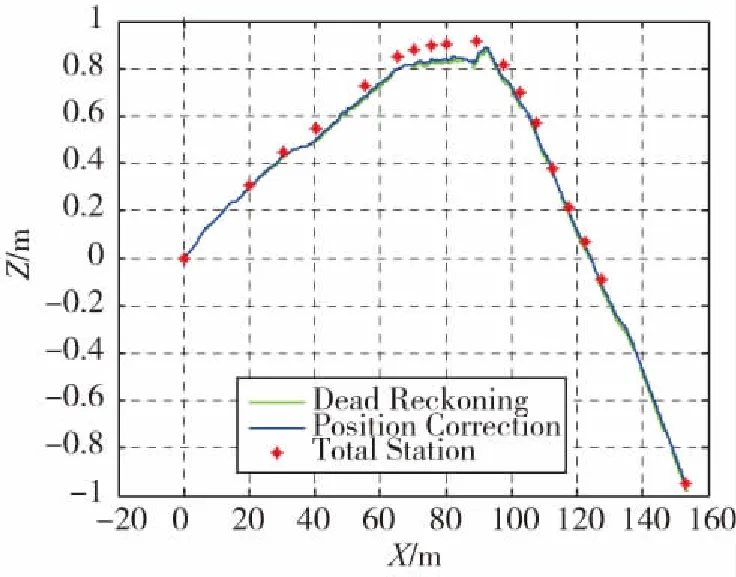
图6 高程轨迹图Fig.6 Altitude trajectory
4.3 试验结果分析
试验结果剩余误差进行分析可能原因如下:
1)试验路面存在裂缝、石子等,因此在行进路程中可能存在里程仪安装轮悬空或打滑情况;
2)试验用车体由于要安装惯导系统、电池组等,因此质量较重,在推行过程中有上下坡情况,因此里程仪标度因数可能在行驶过程中变化;
3)推行过程尽管时间较短,但是陀螺仍在漂移,因此计算的角度误差仅为部分误差。
针对以上原因,可以从硬件及算法两个方面进行改进。硬件方面可以采用提高惯性器件精度或是采用多路里程仪等手段;算法方面可以利用组合导航滤波技术对传感器误差进行实时修正。改进具体方法本文不作讨论。
5 结论
本文提出了一种精密轨迹测量方法。首先对航位推算系统误差方程进行了分析,根据实际使用情况对误差方程进行了简化,提炼出了影响系统精度的主要误差源,针对该误差源引入位置修正技术并进行了相关公式推导。基于以上分析提出了基于航位推算和位置修正技术的精密轨迹测量方法,最后通过试验验证了该方法的有效性,结果表明该轨迹测量方法实测行进153m精度优于0.12m。该方法简单且不易受外界干扰,具有良好的工程使用前景。
[1] 徐辉.GPS接收机与全站仪相结合在长大隧道桥梁施工控制测量中的运用[J].隧道建 设,2008,28(3):355-358.
[2] 鲁超.浅谈公路桥梁施工控制测量中GPS的应用[J].科技研究,2014,5:56.
[3] 郭新愿,刘善华.RTK在工程测量和地形测量中的应用[J].建筑工程技术与设计,2014(6).
[4] 冯宇华.GPS技术在工程测量中的应用[J].四川建材,2016,42(1):252-253.
[5] 王立新,胡文彬.光纤陀螺应用于轨迹测量的实验研究[J].武汉理工大学学报,2002,24(8):50-52.
[6] 段婷婷.光纤陀螺技术用于工程结构形变测量的方法研究[J].数字技术与应用,2013(1):213-214.
[7] 莫文琴,姜德生,胡文彬.基于捷联式光纤陀螺的工程结构三维形变测量方法[J].光学与光电技术,2004,2(4):15-17.
[8] Obanijesu E O, Macaulay S R A.West African Gas Pipeline(WAGP)project:associated problems and possible remedies[M].Appropriate Technologies for Environmental Protection in the Developing World.Springer Netherlands,2009:101-112.
[9] 严恭敏.车载自主定位定向系统研究[D].西安:西北工业大学,2006.
[10] 崔莅杭,张英敏.位置修正技术在航位推算中的应用[J].火力与指挥控制,2012,37(8):100-103.
ResearchonTrajectoryMeasurementBasedonPositionCorrection
CUI Li-hang, CHEN Gui-jin, WANG Yong-gang
(Hubei Sanjiang Space Hongfeng Control Co.,Ltd.,Xiaogan,Hubei 432000, China)
The traditional trajectory measurement is based on equipments like GPS and Total Station.There are some shortcomings of these methods, such as the equipment is hard to set up, the data is discontinuous, and the requirement for environment is high. A trajectory measurement method that uses the position correction technology based on the dead reckoning system is presented. The heading installation deviation angle,pitch installation deviation angle and the scale factor error of odometer can be estimated by the coordinates of the starting point and the end point. After the completion of the dead reckoning, the high-precision data can be obtained by modifying the trajectory with calculated system error. Experiment results show that the method is feasible and the error is less than 0.12m when the system travels 153m.
Trajectory measurement;Inertial navigation;Dead reckoning;Position correction*
10.19306/j.cnki.2095-8110.2017.06.007
U666.12
A
2095-8110(2017)06-0042-07
2016-07-29;
2016-09-05
崔莅杭(1982-),男,工程师,主要从事惯性导航及组合导航研究。E-mail:clhcyf@163.com
