对系统辨识误差鲁棒的自适应复合控制方法研究

杨 军，袁 博，杨博远

(1.西北工业大学 航天学院，西安710072; 2.中国科学技术大学 自动化系，合肥 230027)

对系统辨识误差鲁棒的自适应复合控制方法研究

杨 军1，袁 博1，杨博远2

(1.西北工业大学 航天学院，西安710072; 2.中国科学技术大学 自动化系，合肥 230027)

对基于系统辨识的自校正控制方法来说，其控制性能极大程度受制于辨识精度。针对这一缺点，提出了将变结构模型参考自适应控制与自校正控制相结合的自适应复合控制方法。以二阶线性对象为例，首先给出了极点配置理论下的自校正控制方法，并分析了辨识误差对控制性能的影响，对这一问题，引入变结构自适应控制，并给出了自适应控制律，最后通过仿真证明了这种复合控制方法既能抑制辨识误差的影响，同时也保留了自校正控制参数调整迅速准确的优点。

辨识误差；模型参考；变结构；复合控制

0 引言

始于20世纪50年代的自适应控制是控制理论的重要分支之一，用于解决对象在运行过程中结构与参数及环境有剧烈变化时的控制问题。目前自适应控制主要有两种形式：一种是模型参考自适应控制(MRAC)方法，另一种是自校正(STC)方法[1]。MRAC方法的优点是不需要在线测量对象信息，但自适应律因为没有利用性能指标、受控对象参数及控制参数的相互关系，因此调整效率较低；而STC充分利用了性能指标、受控对象参数及控制参数的相互关系，在受控对象参数辨识准确的前提下，能迅速给出相应的控制参数，具有极高的参数调整效率，其最大的问题就是对参数辨识精度有较高的要求。针对上面两种方法各自的优缺点，本文准备研究如何将MRAC与STC相结合，设计一个对辨识误差具有鲁棒性，同时调参效率较高的控制系统。

从查阅情况来看，目前还未发现研究MRAC与STC复合控制方法的文献，但是单独研究MRAC或STC的文献都很多，其研究涉及自适应律设计、非线性对象、鲁棒性等方面。例如参考文献[2-4]将变结构引入MRAC来解决鲁棒性问题，参考文献[5-7]则研究了采用模型参考自适应方法的辨识问题。

借鉴相关文献的研究成果，本文准备将变结构模型参考自适应控制(VS-MRAC)这种鲁棒MRAC方法与基于极点配置的STC方法相结合，从而设计一个对辨识误差或外界干扰具有鲁棒性，同时调参效率较高的控制系统。

1 复合自适应控制系统设计

1.1 基于极点配置的STC设计与分析

基于极点配置的STC框图如图1所示，控制采用PD反馈。

图1 基于极点配置的STC框图Fig.1 STC block diagram based on pole placement

本文研究的受控对象为典型的二阶线性系统，其传递函数描述如下

(1)

假定其期望的理想特性如下

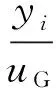
(2)

此时根据极点配置理论，可以给出控制增益的计算公式如下：

(3)

(4)

(5)

校正后真实的系统闭环传递函数如下

(6)

由上面推导可知，当辨识参数无误差时，闭环系统控制性能可达到期望性能；当辨识存在误差时，控制性能会偏离期望特性。

1.2 VS-MRAC设计与分析

为了减小辨识误差的影响，在STC系统之外又引入VS-MRAC，其框图如图2所示。

图2 变结构模型参考自适应控制系统框图Fig.2 Block diagram of variable structure model reference adaptive control system

图2中，可调控制参数分别为前向通道增益K和变结构反馈环节，广义受控对象即为图1所示的闭环控制系统，其形式如式(6)所示。

令

(7)

则广义受控对象可描述为如下的状态方程

(8)

图2中的参考模型为期望的理想模型，因此它与STC设计中式(6)所给的理想闭环传递函数完全一致，即

(9)

令

(10)

则参考模型可描述为如下的状态方程

(11)

定义误差向量

e=x-xm

(12)

对式(12)求导可得误差系统状态方程为

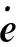
(13)

由于外界干扰或模型参数辨识误差的存在，式(13)中的矩阵A和B为不确定参数矩阵，可记为

A=A0+ΔA，B=B0+ΔB

(14)

其中，A0和B0是无外界干扰或参数辨识误差的标称值，由式(6)可知，此时广义受控对象应该完全逼近式(2)所对应的理想模型，根据前面分析，它也与参考模型相同，即

A0=Am，B0=Bm

(15)

另外，假设ΔA和ΔB满足匹配条件

ΔA=B0E，ΔB=B0F

(16)

式(13)给出的误差系统状态方程可改写为

(17)

VS-MRAC的目的是使误差趋于0，即

(18)

针对误差系统状态方程(17)设计滑模面为

s=Ge

(19)

选择Lyapunov函数为

(20)

对式(20)求导可得

=eTGTG[Ame-Bmr+Bmu+ΔAx+ΔBu]-

≤eTGTG[Ame-Bmr+Bmu]+

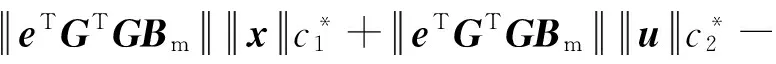
≤eTGTG[Ame-Bmr+Bmu]+

(21)

提出如下控制律

u=ueq+uvs

(22)

式中，ueq=Ke·e+r,

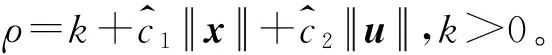
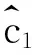
(23)

(24)

将式(22)～式(24)代入式(21)可得

(25)

第一项根据变结构理论，只要Am+BmKe特征值实部为负，则根据Lyapunov方程可解得一个正定阵Q，形式如下

Q=-[(Am+BmKe)TGTG+GTG(Am+BmKe)]

(26)

此时式(25)第一项负定，另外式(25)第二项显然也负定，因此有

至此，可得如下定理：

由式(8)所描述的对象在控制律式(22)和自适应律式(23)、式(24)的作用下，能够跟踪式(11)所定义的参考信号，并且跟踪误差全局渐近稳定。

2 数值仿真

假定图1所示STC中的受控对象为

图2中的参考模型为

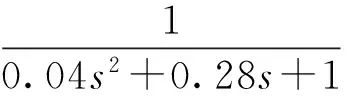
MRAC中，控制相关的参数如下：

在上面的设定下，给定幅值为1的阶跃信号为参考输入，无辨识误差时的仿真曲线如图3和图4所示。

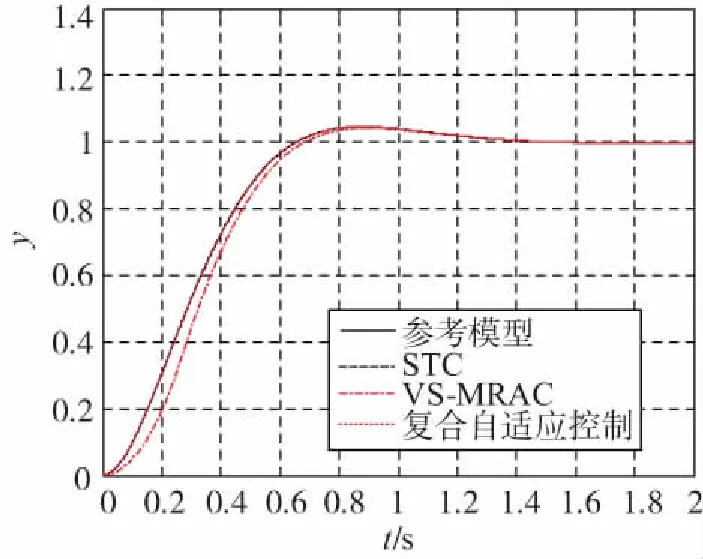
图3 无辨识误差时的阶跃响应Fig.3 Step response without identification error

图4 无辨识误差时变结构模型参考自适应控制的控制指令Fig.4 Control command of VS-MRAC without identification error

从图3可以看出，辨识无误差时，单纯STC与复合自适应控制具有相同的控制性能，与参考模型输出完全吻合，单纯VS-MRAC性能略差。从图4可以看出，复合控制的能量消耗也小于单纯VS-MRAC控制。

下面，再引入辨识误差，假定辨识误差为真实参数的2倍，即Δa1=0.4，Δa2=0.5，此时仿真曲线如图5和图6所示。

图5 有辨识误差时的阶跃响应Fig. 5 Step response with identification error

图6 有辨识误差时变结构模型参考自适应控制的控制指令Fig.6 Control command of VS-MRAC with identification error

从图5可以看出，辨识有误差时，复合自适应控制的输出最接近参考模型输出，下来是VS-MRAC，STC较差，这与理论是相符的。从图6可以看出，复合控制的能量消耗也小于单纯VS-MRAC控制。

3 结论

本文将VS-MRAC方法和基于极点配置的STC方法相结合，形成新的复合自适应控制方法，着重给出了复合控制方法中VS-MRAC的设计方法，并通过最后的仿真证明了所提的复合自适应控制方法综合了STC与VS-MRAC的优点，既能很好地抑制辨识误差等未知干扰的影响，同时也保留了自校正控制参数调整迅速准确的优点，是一种最优控制与鲁棒控制相结合的尝试。未来要进一步做的工作一方面是在变结构项中引入消颤算法，另一方面从理论上进一步研究最优控制与鲁棒控制相结合的方法。

[1] 周涛，王磊. 基于跟踪微分器的模型参考自适应控制[J]. 电光与控制， 2012，19(10):46-49.

[2] 鹿存侃，闫杰，杨淑君，等.基于模型参考的高超声速飞行器自适应滑模控制[J]. 计算机测量与控制，2009，17(7)：1320-1322.

[3] 刘涛，闫斌斌，顾文娟，等.基于滑模变结构的高超声速飞行器控制律设计[J]. 飞行力学, 2014，32(4): 325-328.

[4] 林岩，毛建琴.鲁棒变结构模型参考自适应控制器的分析与设计(I)[J]. 控制理论与应用,2000，17(4):513-518.

[5] 王庆龙，张崇巍，张兴.交流电机无速度传感器矢量控制系统变结构模型参考自适应转速辨识[J]. 中国电机工程学报, 2007，27(15): 70-74.

[6] 孙先仿，张志方.连续系统的模型参考自适应辨识新方法[J]. 自动化学报, 1996，22(1): 115-117.

[7] 摆玉龙，杨利君，柴乾隆.基于系统辨识的模型参考自适应控制[J]. 自动化与仪器仪表, 2011(3): 23-26.

[8] 林岩，毛建琴.具有理想跟踪特性的鲁棒变结构模型参考自适应控制[J]. 自动化学报, 1999，25(2): 191-198.

ResearchofAdaptiveHybridControlMethodwithRobustnessonSystemIdentificationError

YANG Jun1, YUAN Bo1， YANG Bo-yuan2

(1.College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2.Department of Automation, University of Science and Technology of China, Hefei 230027, China)

For the self-tuning control method based on system identification, the control performance is greatly affected by the precision of identification. To overcome this shortcoming, this paper proposes an adaptive compound control method based on variable structure model reference adaptive control and self-tuning control. Taking second order linear object as an example, the self-tuning control method based on pole assignment theory is firstly given, and the influence of identification error on control performance is analyzed. For this problem, variable structure adaptive control is introduced, and the adaptive control law is given. At last, the simulation results show that the composite control method can not only suppress the influence of the identification error, but also retain the advantages of rapid and accurate parameter adjustment of self-tuning control.

Identification error; Model reference; Variable structure; Hybrid control

10.19306/j.cnki.2095-8110.2017.06.004

V249.1

A

2095-8110(2017)06-0024-05

2017-04-22；

2017-06-18

国家自然科学基金联合基金项目(SupportbyNSAF)(U1630127)

杨军(1965-)，男，教授，研究方向为飞行器导航、制导与控制。E-mailyangjun8@sina.cn