全境学习 玩出精彩——以《理想国的果实》为例

■ 武汉经济技术开发区洪山小学 张 虹

全境学习 玩出精彩
——以《理想国的果实》为例

■ 武汉经济技术开发区洪山小学 张 虹

美国著名教育家杜威认为“课程即活动”。武汉经济技术开发区洪山小学数学组致力于将游戏融入数学校本课程，开发出六个年级全套共12册《玩数学》校本教材，同时，又在编写数学校本课程的过程中，开发数学游戏，充分调动学生对数学的兴趣，在游戏中培养学生的数感。在2016年，洪山小学又引进了《超脑麦斯STEAM课程》，将其融入《玩数学》课程之中。这是一套符合STEAM理念、融合数学核心素养、强调全程动手做数学、着重数学创客教学的小学数学创造力课程，以培养学生的高阶思维能力和创造力为目标，以“做数学、说数学、玩数学”为理念，让学生动手操作解决问题，有效开发他们的右脑功能，促进其全脑思维协调发展，从而发挥大脑的无限认识能力和创造功能，激发学生的创造潜力。

本课程根据小学生的年龄特点和学习数学的规律，设置了7大主题的学习内容，搭配螺旋式课程规划和完整的课程体系，让学生的应用、分析、评价和创造等高阶思维不断经历挑战，激发创造的火花。本文以其中《理想国的果实》为例，阐述通过整体的设计，创设全境学习，让学生玩出精彩的教学理念。

一、教学设计

1．学习目标：

①让学生在活动中认识阿基米德多面体，在拼多面体的过程中思考拼装中的数学问题。

②在活动中培养学生的动手操作能力和合作意识，提高对数学的兴趣。

2．学习重难点：

学习重点：合作拼装，并用算式表示多面体中各图形的数量。

学习难点：用算式表示多面体中面、线段、点的数量。

学习准备：每个小组四套材料，每套材料包含5个正六边形、3个正五边形、若干根连接小棒。

3．学习过程：

①准备活动

清理出红色、绿色和连接棒。

（设计意图：整理材料可以训练学生的秩序意识，同时在整理的过程中，熟悉正五边形和正六边形的特征，便于后面的拼装以及研究。）

②操作思考

小试牛刀：1人单独拼，1绿+2红。

活动后此组合不拆散，直接往上加。

（设计意图：热身活动的设计，是为了让学生初步感受拼装材料的方法，学会使用连接小棒，将两片正多边形连接起来，并感知这些正多边形的边长长度相等。）

活动一：2人合作拼，6绿+10红。（半球）

1．拼之前先观察，这个图形有什么特点？怎样分工拼会比较有效率？小组交流。

（设计意图：认真的观察才能够正确的拼装，合理的分工才能够事半功倍，磨刀不误砍柴工，操作之前一定要做好充分的准备。每个小组有四套材料，如果不是4人小组，要特别提问该怎样分工，让学生知道有时候材料并不是数量合适的，遇到这样的情况该如何处理。）

2．汇报分工的方法，再动手操作，操作时思考：用了多少个正五边形？多少个正六边形？用算式怎样表示？

3．学生活动。

4．活动后交流：正五边形和正六边形分别有多少个，算式是什么。

（1）正五边形。

预设1：数数的方法。

预设2：把材料合起来的方法，3×2。

预设3：以绿色为底，1+5。（课件演示）

（设计意图：在操作活动中，如果有2个或2个以上小组完成，做一个暂停，强调做完的小组用观察的方式检查拼装是否正确，并思考算式，让学生养成良好的操作习惯。另外，在本次交流中，旨在让学生领悟对图形的观察是有一定顺序的，先把学生的算式记录下来，再让学生讲清算式的来历，引导学生有条理的发言。）

（2）正六边形。

预设1：以绿色为底，一圈圈的观察，5×2。

预设2：一列列的观察，2×5。

思考：5×2和2×5的意义是不是一样的？

5．小结：可以横向一圈圈观察，也可以纵向一列列观察。

（设计意图：不同方向的观察，得到不同的结果，但又可以用相同的算式来表示，数学真是一件很奇妙的事情。在这个比较中，能够进一步深化学生对乘法意义的理解。）

活动二：4人合作拼，12绿+20红。（球体）

1．出示问题：

正五边形和正六边形分别有多少个，算式是什么。

2．学生带着问题开展活动。

3．小组交流，指名汇报。

（1）正五边形。

预设1：以绿色为底，1+5+5+1。

预设2：以红色为底，3+3+3+3。

（2）正六边形。

预设1：以绿色为底，5+5+5+5。

预设2：以红色为底，4+4+4+4+4

一列列的看，2×10。

4．小结：不仅可以朝不同方向观察，还可以以不同颜色为底从不同角度观察。

（设计意图：通过第一次活动，学生知道了可以从不同的方向来观察多边形的个数，并运用到整球的计算中来。但同时，有可以引导学生转动整球，从不同的角度来进行观察，可以以绿色的正五边形为底，也可以以红色的正六边形为底，都可以观察出不同的结果。）

思考：刚才我们先找出有12个绿色，老师还有一个方法，用12×5÷3也可以求出红色的个数，为什么呢？

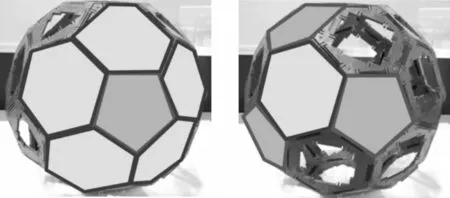
（设计意图：这是一个非常巧妙的方法，利用正五边形的个数、根据球的排列规律和环绕情况，计算出正六边形的个数。每个绿色周围围绕了5个红色，12个绿色周围就有12×5个红色，但每个红色旁边围绕了3个绿色，说明每个红色都被重复计算了三遍，所以12×5÷3，才是红色的个数。）

（三）课外延伸

微课介绍阿基米德多面体：两种或两种以上的正多边形为面的凸多面体。共有13种，如：足球。

今天拼装的足球形状的阿基米德多面体又叫做“566”型的阿基米德多面体。“566”的含义是什么？

（设计意图：通过微课将球体进行延伸，让学生认识阿基米德多面体，美丽的阿基米德多面体会激发学生极大的兴趣，而对型号设定的思考，作为课外的延伸，让学生将课上的知识带到课下，可以从更多的渠道去了解阿基米德多面体，感受数学的古典美。）

（四）全课小结

你在今天的活动中有什么收获？

（五）板书设计：

二、课后反思

超脑麦斯作为洪山小学《玩数学》校本课程的一个内容，旨在创设全境学习，通过整体的设计，打造适合学生学习与发展、利于教师成长与提高的数学创意课程，培养和开发学生的高阶思维，促进学生的创造力发展。

（一）提升共同成长力

片段一

全班学生在讨论半球中有多少个正五边形（绿色）。

生1：底下有1个，中间一圈有5个，所以用1+5。

师帮学生转动一下身体,“在交流时我们是和全班同学进行交流，你不是只说给老师听，所以请面向同学最多的方向。”

生1准备再说一遍。

师轻声：“这次你再说之前要提醒大家认真倾听，待会儿你会点同学来提问或复述哦！”

生1提出了复述的要求并很认真地表达了自己的想法。

生1：“大家听懂了吗？不懂可以提问。懂了可以举手再说一遍。”

生2复述了一遍。

师：“你认为他表达的是你的想法吗？”

生1：“是的。”

师：“谢谢你们！后面的内容咱们就都像这样交流哦！”

【反思】

学生的学习过程是一个共同成长的过程，为了使学生们形成更好的学习共同体，我引导学生学习如何和自己的同伴进行交流。在交流的过程中，我们会关注到倾听的质量，会关注到表达的清晰度，以形成良好的生生互动。小组合作学习的力量是不可估量的，而利用每一节课去实现小组的真合作，才能发挥每位学生的学习力，真正做到1+1＞2，而老师对合作的有效指导和关注，是提高合作效率的助燃剂。

（二）找准学习发展区

片段二

师：观察你们所拼装的半球，使用了几片正六边形的材料？也就是红色？

生1：两个人的材料都用完了，每人5片，5+5=10。

生2：我是两个相对的红色一起数的，这里有两个，这里有两个，这里有两个……（混乱的旋转半球）2×5。

生3：我是一圈圈观察的，每圈 5个，有2圈，5×2。

生4：我是一列列观察的，每列2个，有5列，5×2.

师：这四种方法，哪些是通过观察图形得到的算式？（3和4）哪些方法更有条理？（3和4）后两种方法同样都是 5×2，意义相同吗？

生：不一样，前面的5×2是横着观察的，代表2个5，后面的5×2是竖着观察的，代表5个2.

师小结：看来我们在思考时一定要注意有序，这样才能不重复不遗漏，按照不同的方向观察也会得到不同的方法。

【反思】

学生在整节课中会有几次操作活动和几次思考行为，为了让学生在每一次思考和交流后有所收获，必须根据学生的学习发展特点将活动设计出层次。在第一次活动后交流时，要引导学生优化高阶的思维方法，通过对乘法算式意义的理解，领悟有序思考的重要性，从而提炼出不同的观察方向会得到不同的方法。只有在前面的活动中找准学生的学习发展区，才能帮助学生在后面的学习中更轻松的探索。

(三）激发潜在发展力

片段三

师：整球中用到了多少个正六边形（红色）

生 1：我的方法是 12×5÷3。

师：你的算式非常奇特，竟然出现了除法。能给大家解释一下是什么意思吗？

生1：大家看，每个绿色周围围绕了5个红色，12个绿色周围就有12×5个红色，但每个红色旁边围绕了3个绿色，说明每个红色被重复算了3次，所以要÷3，这样就能算出红色的个数了。

师：你问问大家有没有问题.

生1：大家有没有问题？

生 2：为什么要“×5”？

生1：12个绿色，每个绿色旁边有5个红色，所以12×5。

生 3：那为什么要“÷3”呢?

生1：你们看，这个红色旁边有3个绿色，这个绿色算了它，这个绿色也算了它，这个绿色也算了它，它不是被算了三次吗？算重复了，所以要“÷3”。

师适时播放课件，为全班同学清晰的演示。

生4：老师，如果已知红色的个数，我们是不是也可以用同样的方法，去算绿色的个数呢？

师：那你试试看。

生 4：20×3÷5。

【分析】

本节课，几乎学生所有的算式都是按照某种方向、或是变换观察角度，而这位同学在最后出示的这种方法，却显示了更为强大的思维能力。他从足球的排列规律去思考，发现正五边形和正六边形的个数之间存在某种联系，正五边形由于有五条边，所以每条边上有一个正六边形，而正六边形是每隔一个排列一个正五边形。因此用先乘再除以重复次数的方法也能算出正六边形的个数。由此方法延伸和运用，知道正六边形个数，也能求出正五边形个数——每个红色周围有3个绿色，20×3，每个绿色周围有5个红色，所以被重复算了5次，要“÷5”。多么巧妙的方法啊！这个方法的出现，既是偶然，其实也是必然，在学生整节课的大量的操作活动中，并不是单纯的操作，每次还带着问题，在建构足球的过程中，学生其实已经对足球的构造非常熟悉了，数形结合，充分放飞了学生的想象力，从而出现了如此精妙的方法。如果仅有操作没有思考，或是仅仅观察思考没有实际的操作，学生都无法得到如此深刻的体验。只有在玩中学，才能充分激发学生的潜在发展力。

数学需要激趣，数学需要情境。《玩数学》课程正是秉承着这样的理念，将数学学习置于有趣好玩的情境之中，让学生乐学善思、有效合作。在理想国中，摘取的不仅仅是看得见摸得着的“阿基米德多面体”这枚果实，更是看不到的思维力之果、合作力之果、创造力之果。在数学的国度里，探索数学的奥秘、体会数学的价值、感受数学的魅力。数学好玩，玩好数学，玩出精彩。

责任编辑 郑占怡