基本不等式教学实录

安徽省肥东第一中学 孙光元

安徽省肥东第一中学 孙光元

师：你能通过观察上述几组式子，判断其大小关系吗？

生：都是大于。

师：大家同意他的观点吗？

生1：同意。

生2：不同意。

师：那么我们如何评价谁对谁错呢？

生：可以作差比较。

师：很好。那么我们一起动手来作差，看看究竟哪个结论是正确的。（请一位同学在黑板上板演，其他同学在下面演算）

师：通过大家的验证，我们发现 。那什么时候这个等号是成立的啊？

生：当 的时候，不等式的等号成立。

师：a，b有什么限定要求吗？

生：只要是实数就可以。

师：观察这个不等式不难发现，当 时，等号成立，等号如果成立也说明 。我们可以这样表述：对于任意实数a，b，有，当且仅当 时，等号成立。（板书上述内容）

师：那么我们可以借助几何图形解释这个不等式吗？（展示多媒体）

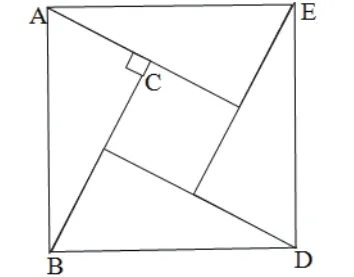
师：请同学阅读课本98页第三自然段证明基本不等式的方法。如果是你，你如何证明上述不等式成立呢？

生：还是可以通过作差比较来加以证明。

师：很好，课本中给出了一种全新的证明方法——分析法，这在以后选修的课程中我们将进一步学习。其实我们完全可以借助作差比较来证明。

师：你能用自然语言描述基本不等式吗？

生1：两个正数的和不小于这两个数乘积开方的两倍。

生2：两个正数的算术平均数不小于其几何平均数。

师：两位同学说得都很好，那么我们还能用图形对其进行解释吗？请同学们阅读课本98页，探究并思考你如何用图形来解释基本不等式。

师：那应该怎么描述这种不等关系呢？

生3：圆的半径不小于其半弦长。

师：很好。我们给出基本不等式的两种解释：（1）两个正数的算术平均数不小于其几何平均数；（2）圆的半径不小于其半弦长。我想通过这样的解释，大家对于基本不等式都有了更深的理解。那么它可以用来解决什么样的问题呢？

师：在这里，我们看见是求两个正数之和的最小值。那么它和我们今天学习的不等式有什么关系呢？

生：基本不等式的形式中，一边就是数的和，另一边就是数的乘积。

师：观察得很仔细，一边是两个正数的和，而另一边是两个正数的乘积。那么怎么转化成常数呢？

师：你能用什么方法求其最大值呢？

师：很好，这是一个很好的方法，那么今天我们学习了基本不等式，你能用基本不等式解决这一问题吗？

生：可以解决。

师：那请你们用基本不等式的方法来求其最大值，课后用二次函数的方法求解，然后对比一下它们的优缺点，下节课我们请同学们谈谈自己的感受。（请一位同学上黑板板演，其他同学在下面完成，教师评价学生的解题过程，并纠正其不足的地方）

师：请刚才这位板书的同学谈谈你是怎么想的。

生：刚才通过例1我发现，求和的最小值只要乘积是定值就可以了，这一题是求乘积的最大值，我就想能不能找到和的定值，然后发现是定值。

师：这位同学的思路很清晰。那么你们能总结出利用基本不等式求最值的方法了吗？

生1：要求和的最小值，就要找到乘积的定值，要求乘积的最大值，就要找到和的定值。

生2：还要求这些式子中的数要是正数。

师：还有吗？我们要取得最值，也就相当于不等式的等号要成立哦！

生：还要求当且仅当 时，等号成立。

师：现在我把大家说的总结一下：首先，我们要使用基本不等式，就要满足数或者式子是正的，即一正；其次，我们发现要求和的最小值，要有乘积形式的定值，求乘积的最大值，就要有和形式的定值，即二定；最后，要让式子取得最值，要注意等号能够成立，即三相等。以后我们要利用基本不等式解决最值问题时应注意以上三点。

（展示多媒体）变式练习：

（利用多媒体投影学生的书写过程，让学生相互评价）

生3：我们最后要说明等号什么时候成立。

师：同学发现了很多问题，总结得也很好。看来大家对基本不等式学习的还是不错。那么你们能总结一下今天我们都学到了什么吗？

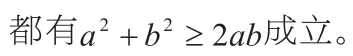
生2：我们还学习了利用基本不等式求式子最值的方法，还要注意一正、二定、三相等。

生3：我们还了解了两个不等式的几何解释。

师：通过这节课的学习，大家都是有所收获的。希望大家课后完成这几组练习。

（展示多媒体）习题3.4 A组第一题：