3D MIMO-OFDMA系统中基于垂直波束成形的能效优化算法

2017-12-04李汀仇林杰季薇

电信科学 2017年11期

关键词：能效波束基站

李汀，仇林杰，季薇

（南京邮电大学通信与信息工程学院，江苏南京 210003）

3D MIMO-OFDMA系统中基于垂直波束成形的能效优化算法

李汀，仇林杰，季薇

（南京邮电大学通信与信息工程学院，江苏南京 210003）

针对三维多输入多输出（3D MIMO）正交频分多址（OFDMA）系统，提出了一种能效优化算法。该算法在垂直波束成形技术下，以能量效率最大化为目标，通过调整资源分配、功率分配、天线的波束下倾角来提高系统能量效率。根据分数优化理论，将复杂的分数优化问题转化为较易求解的整式优化问题，然后引入拉格朗日乘子通过不断迭代得到能量效率的最优值。仿真结果表明，所提算法在较少迭代次数下可以获得更高的能量效率。

三维多输入多输出；垂直波束成形；能量效率；分数优化理论

1 引言

随着无线通信技术的飞速发展，各种新型传输技术的使用以及传输方案的设计都可以不同程度地提高系统的吞吐量，这使得移动数据的传输速率呈现指数级增长趋势，但是传输速率飞速增长的同时，能量消耗速度急剧增加，通信设备的成本也随之不断提高。同时，无线通信系统巨大的能量消耗产生了大量的气体排放，引起环境污染。因此，在传输过程中，要充分考虑能量损耗因素，实现绿色通信，这也体现了可持续发展的思想。

在通信系统中，由于基站和用户终端的数量庞大，产生了巨大的能量损耗，其中，基站产生的能量占据了绝大部分比例，随着4G网络的不断完善以及5G网络的兴起，通信产业将会产生更多的能量损耗。大量的能量被消耗意味着巨额的电费成本开支，在整个网络通信过程中，电费开支大约占总成本的20%～30%，并且随着用户数量的增长和用户对服务质量要求的不断提高，电费开支占总成本的比例会进一步提高。对于运营商而言，为了使利润持续增长，需要尽可能地降低能耗来减少运营的成本，从而提高收入。对于终端用户而言，提高能量效率能够延长设备的使用寿命。致力于推进5G发展的欧洲研究小组METIS明确提出，能量效率应作为5G的关键指标之一[1]。5G系统中能量效率的研究在多蜂窝系统、超蜂窝系统、中继系统、多用户系统等不同场景中都展开了广泛的研究[2-6]。3D MIMO（three dimensional multiple-input multiple-output，三维多输入多输出）技术是5G的重要技术之一，因此，在3D MIMO场景下探讨能量效率也具有重要的研究意义。

对于通信系统传输过程的研究，能量效率问题受到越来越多的关注。参考文献[7]证明了在OFDMA无线系统中，能量效率会随着信道增益及子载波数目的增加而增加，随着电路能耗的增加而减少。在此基础上，提出了功率及子载波资源分配方案，该方案提高了系统的能量效率。参考文献[8]研究了SISO-OFDM系统下行链路的能效资源分配问题，将非凸优化问题转化为凸优化问题，给出了有效的资源分配算法。但考虑的场景是SISO（single input single output，单输入单输出）系统，在MIMO场景下该方案并不适用。参考文献[9]基于MIMO-OFDMA无线通信系统提出了一种服务质量约束条件下的功率、子载波资源分配方案，该方案可以实现系统能效性能的最大化。在 3D MIMO下行链路传输系统中，基站天线发送给小区用户的波束下倾角也影响系统的能量效率[10,11]。大多数能效优化的文献都是首先以系统总的吞吐量与总功耗的比值得到系统的能量效率，能效优化问题实质就是一个分数优化问题，然而直接求解此分数优化问题通常比较困难。参考文献[12]将分数优化问题转化为等效的整式优化问题，这样可以更有效地解决优化问题。

在调研上述文献之后，本文针对 3D MIMO-OFDMA这一新型系统，充分利用垂直维的自由度，综合考虑功率分配、资源分配以及天线的波束下倾角，将能效最大化的分式优化问题转化为整式优化问题，提出了一种基于拉格朗日乘子法的能效优化迭代算法，用于求解能效最优时的功率和资源分配方案以及天线的波束下倾角。

2 3D MIMO信道模型和天线阵列结构

本文采用的信道模型为三维空间信道模型（three dimension spatial channel model，3D SCM）[13]。与传统2D SCM只考虑水平维度的到达角和离开角不同，3D SCM还考虑了垂直维的自由度。3D SCM架构如图1所示。

假设发送端和接收端之间有N条主径，每条主径有M条子径。在发送端，每条路径都有水平离开角（azimuth angle of departure，AOD）和垂直离开角（elevation angle of departure，EOD）；在接收端，每条路径都有水平到达角（azimuth angular of arrival，AOA）和垂直到达角（elevation angle of arrival，EOA）。发送天线s经过第n条主径到达接收天线u的信道系数可表示为：

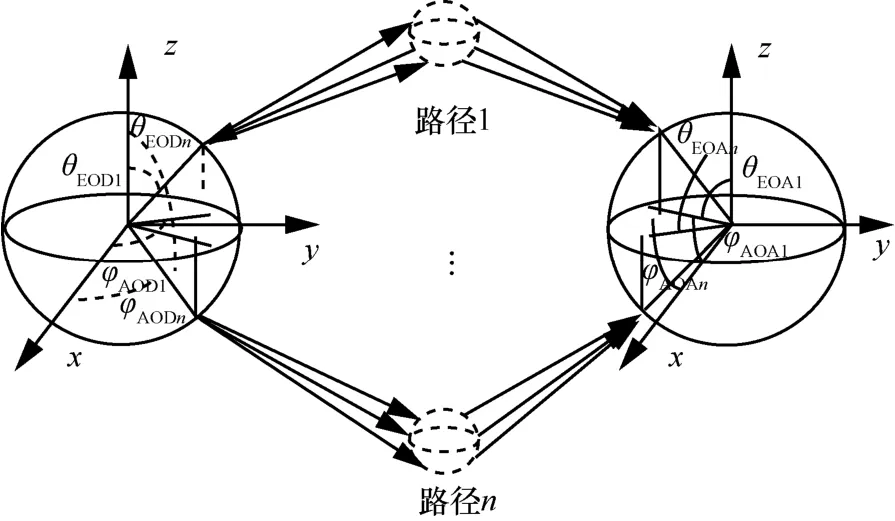
图1 3D SCM架构

其中，Frx,u,θ和Frx,u,ϕ分别代表第u根接收端天线的垂直基底方向极化复增益和水平基底方向极化复增益；Ftx,s,θ和Ftx,s,ϕ分别代表第s根发送端天线的垂直基底方向极化复增益和水平基底方向极化复增益；分别代表第n条主径的第m条子径的 EOA和 AOA；分别代表第n条主径的第m条子径的和EOD和AOD；κ为交叉极化鉴别率（cross polarization power ratio，XPR）；drx,u和dtx,s分别代表接收端第u根天线和发送端第s根天线的位置矢量；vn,m代表第n条主径的第m条子径的多普勒频率分量。

发送天线s的极化复增益矩阵可以进一步写为：

其中，α表示天线极化角度。

3D MIMO系统根据三维信道状态信息，可以调整基站端有源天线的三维波束成形权值，使波束的主瓣在三维空间内更好地对齐所要传输的用户，从而提高用户接收到的功率和用户端的信干噪比，进而提高系统总的吞吐量。图2为多用户3D MIMO系统波束成形示意。从图2中可以看出，若采用传统的2D MIMO波束成形技术，只能区分用户1和用户2，而很难区分具有相同水平位置的用户2和用户3。但是，对于基于有源天线的3D MIMO波束成形技术，虽然用户2和用户3具有相同的水平方位角，但是他们具有不同的垂直仰角，3D MIMO可以利用垂直维度的信道状态信息来区分用户2和用户3。因此，基于有源天线的3D MIMO系统可以获得更高的系统吞吐量。

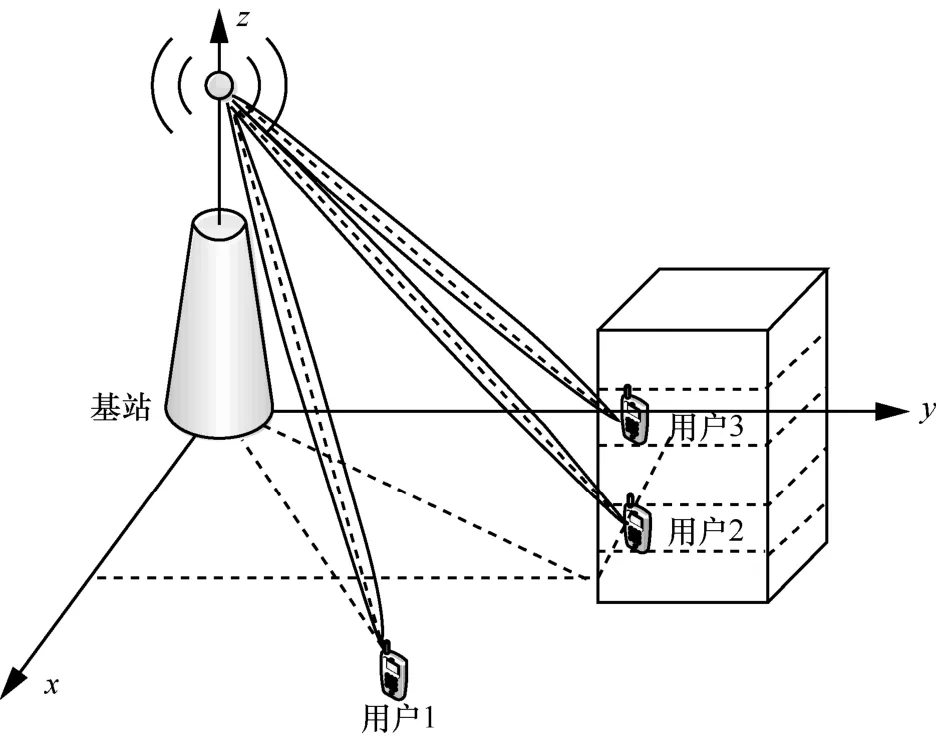
图2 多用户3D MIMO系统波束成形示意

3 下行链路基站能量损耗模型

本文考虑实际下行链路传输过程中的基站能量损耗模型。在下行链路传输过程中，天线发送功率在系统总的能量损耗中占据了较大部分，在传统多天线技术中系统的能量损耗也主要考虑功率放大器（以下简称功放）上消耗的能量，但是每根天线单元中的电器设备也占据着一定的能量，这些能量也是不可忽略的，尤其是当天线数目比较多的时候。根据LTE基站的模型，下行链路传输过程中各电路模块组成模型如图3所示。

图3 下行链路传输过程中各电路模块组成模型

[14]可知，基站每根天线在下行链路工作时，其平均功率消耗主要由两部分组成：电路能耗和功放能耗。电路能耗cP是指电器硬件设备消耗的能量，这些电路设备包括数模转换器（DAC）、滤波器、混频器、锁相环等。故发送端电路功耗的计算式为：

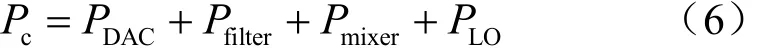
其中，PDAC表示数模转换器的功率损耗，Pfilter表示滤波器的功率损耗，Pmixer表示混频器的功率损耗，

P 为锁相环同步所需要的功率损耗。根据参考文献[15]，功放能耗模型在实际系统中的取值见表1。

表1 功放能耗模型在实际系统中的取值

功放能耗是所有功率放大器的能量消耗PPA，它随着天线发送功率tP线性变化。它们之间的关系式近似表示为：

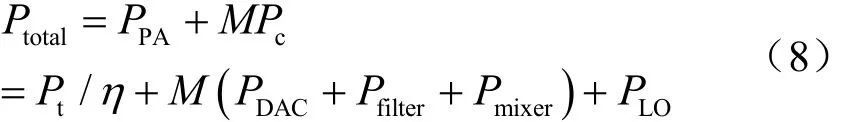
其中，M为天线根数。

4 系统模型

本文所考虑的系统为下行单小区 3D MIMO-OFDMA系统，如图4所示，系统中有一个基站配置S根天线和M个接收用户。假设信道为块时变的慢衰落信道，并且基站知道信道状态信息（channel state information，CSI）。系统总的频谱资源被划分为每组N个正交的资源模块，每个资源模块由K个频率上相邻的子载波组成。

图4 3D MIMO单小区多用户系统

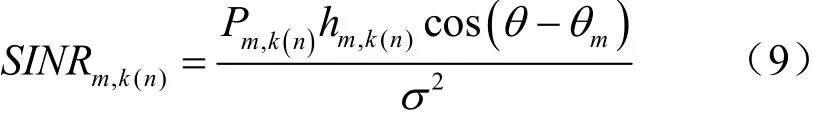
由香农定理知，第n个资源模块的第k个子载波发送给第m个用户的传输速率为：

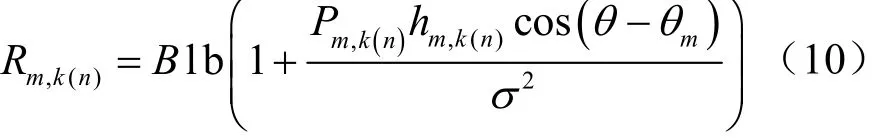
其中，B表示子载波的带宽。

故第n个资源模块发送给第m个用户的传输速率为：

第n个资源模块发送给第m个用户总的功率为：

则总的系统吞吐量可以表示为：

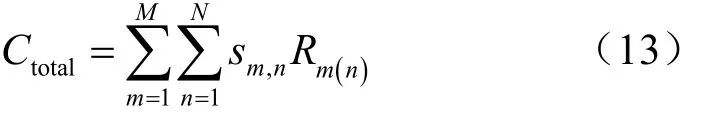
其中，sm,n表示第n个资源模块是否分配给了第m个用户，

由式（13）可知，系统总的吞吐量与功率分配、资源模块分配以及天线的波束下倾角有关，因此把总的系统吞吐量记为这里P、S、θ分别代表功率、资源模块、波束下倾角分量。此系统下，总的功率损耗计算式为：

其中，cP为天线持续的电路损耗功率，其包括发送滤波器、混频器、频率合成器、数模转换器的电路损耗功率，与实际的发射功率无关。也就是说，式（14）的第一项表示被激活的天线所消耗的总能耗，第二项表示基站的射频放大器的总功率能耗。η表示功放的漏极效率，PLO表示与发送端天线根数无关的同步器的能耗。故由式（14）可知，系统总的能耗与功率分配、资源模块分配有关，把系统总的功率能耗记为因此能量效率的计算式为：

可记为：

其中，C1是确保系统能够满足用户m至少需要的最小传输速率Rm的约束条件。C2是下行链路基站发送功率约束条件，PT表示基站发出的总功率。C3和C5是确保每个资源模块服务于一个用户。C4是确保基站发送功率为正值。C6是波束下倾角的约束条件。

5 能效优化迭代算法

式（17）的目标优化函数为非凸函数，且约束条件较多，直接求解此最优化问题基本上是不可行的，为了得到能效优化资源分配算法，根据分数优化理论[19]首先对目标函数进行变换。

因此有：

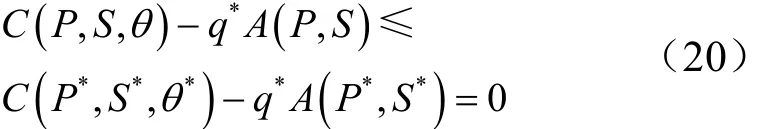
上述计算式表明：

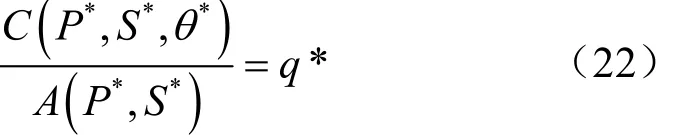
能效优化问题等效的最优化问题如下所述：

所等效的最优化问题式（23）是一个联合优化问题。为了得到有效的资源分配算法，对如何获得进行讨论。

首先，对发送给小区中心用户的波束下倾角固定，先对资源和功率分配进行优化。则：

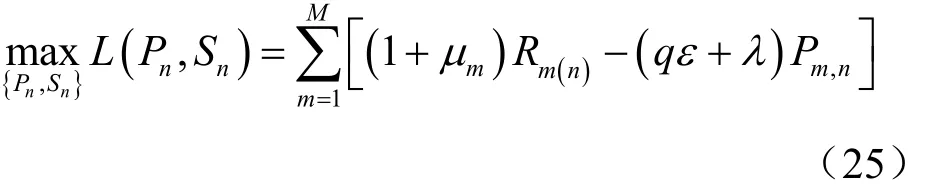
则根据KKT（Karush-Kuhn-Tucker，卡罗需—库恩—塔克）条件可得：

将式（26）代入式（25），则式（25）可以写为：

则最优化资源分配方案可以通过式（28）得到：

在资源分配和功率分配之后，把式（26）和式（28）代入式（24），然后对θ求偏导得：

拉格朗日乘子在第l次迭代的更新式为：

本文提出了一种迭代算法以解决式（24）的最优化问题。在算法实现中，假设信道状态信息是已知的，并且子载波的信道带宽小于相干带宽。迭代资源分配算法流程如下。

计算每个资源模块 RB n=1toN发送给用户m时的增益

for 每个用户m=1 toM

end for

根据式（29）计算*θ

else

Convergence=false

end if

until Convergence=true或者达到最大迭代次数

6 仿真分析

对3D MIMO-OFDMA能效性能进行仿真分析。仿真中的2D MIMO信道模型采用参考文献[20]给出的2D SCM参数，3D MIMO信道模型采用参考文献[13]给出的3D SCM参数。天线阵列模型为均匀线性阵列（uniform linear array，ULA），天线阵元的间隔为半个波长，发送端天线数为2，接收端天线数为2。假设用户均匀分布在小区中，且用户在小区内不移动。系统中有3个用户和8个资源模块，每个资源模块有12个子载波（在实际系统中子载波和用户数目一般都很大），子载波带宽为B=10 kHz，系统带宽 W=5 MHz，基带信号采用QPSK调制。小区半径为300 m，基站高度为30 m，用户受到的噪声为均值为0、方差为 0.1的高斯白噪声。基站的能量损耗参数见表1，功放的漏极效率η=0.35。

图5给出了在本文所提能效优化迭代算法下，作为目标函数的能量效率值随迭代步数的变化曲线。从图5中可以看出，在刚开始的几次迭代过程中，能量效率值波动比较明显，但随着迭代步数的增加，能量效率值波动渐渐平稳，最终趋于稳定值。这是因为在搜寻最优解时，最初的搜索点一般不是最优解，但随着不断迭代变化，搜寻的点将会不断向最优解靠拢。仿真结果显示，在通过较少的迭代步数之后，就能得到原最优化问题的最优解。

图5 目标函数的能量效率值随迭代步数的变化曲线

图6比较了3D MIMO系统和2D MIMO系统的能效性能。从图6中可以看出，随着信噪比的增加，2D MIMO系统和3D MIMO系统的能量效率也不断增大。在相同信噪比的条件下，3D MIMO系统能效性能要明显优于2D MIMO系统。这主要是因为3D MIMO系统垂直维自由度提高了系统的传输速率，因此能量效率也比2D MIMO系统高。

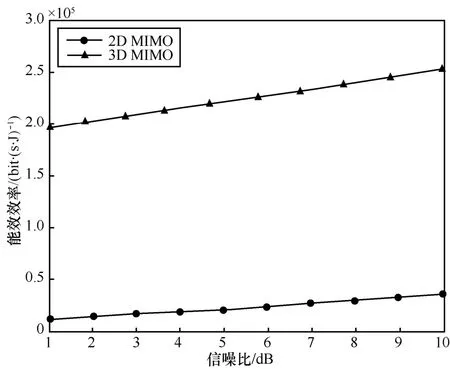
图6 3D MIMO系统和2D MIMO系统能效性能比较

图7比较了3D MIMO系统下本文所提能效优化迭代算法和参考文献[21]所提的最大化频谱效率算法的能量效率随着最大发送功率约束变化的情况。从图7中可以看出，随着基站最大发送功率约束的增加，以最大化能量效率为目标的算法和以最大化频谱效率为目标的算法，系统总的能量效率均随着基站最大发送功率的增加而增加，而且可以明显看出本文所提能效优化迭代算法的能量效率高于最大化频谱效率算法的能量效率。

图7 不同发送功率限制下算法的能效性能比较

7 结束语

本文对3D MIMO-OFDMA下行链路传输系统的能量效率进行了研究。与传统的2D MIMO系统相比，通过垂直波束成形动态调整发送给用户的波束下倾角以进一步提高系统的能量效率。为了求解能效优化问题，根据分数优化理论，将原始的分数优化问题转化为等价的整式优化问题，然后通过资源分配、功率分配和波束下倾角调整进行联合优化。对于求解等效的整式优化问题，本文提出了基于垂直波束成形的资源分配迭代算法进行求解。根据引入拉格朗日乘子表示的拉格朗日函数得到每次迭代的资源分配、功率分配方案以及波束下倾角的值，然后通过不断迭代直到达到最大迭代步数或者算法收敛，从而得到最大的能量效率值。仿真结果表明，本文所提算法能够有效提高系统的能量效率，系统的能效性能与2D MIMO系统相比有明显提高，同时也比3D MIMO系统最大化频谱效率方案的能量效率高。

参考文献：

[1] FALLGREN M, TIMUS B. Scenarios, requirements and KPIs for 5G mobile and wireless system[S]. METIS deliverable D, 2013.

[2] 牛志升, 龚杰, 周盛. 能效与资源优化的超蜂窝移动通信系统基础研究[J]. 电信科学, 2014, 30(12): 34-47.NIU Z S, GONG J, ZHOU S. Research on energy efficiency and resource optimized hyper-cellular mobile communication system[J]. Telecommunications Science, 2014, 30(12):34-47.

[3] 郭杨波, 张治中, 胡昊南, 等. 关于5G中继技术的节能算法研究[J]. 电信科学, 2015, 31(3): 55-60.GUO Y B, ZHANG Z Z, HU H N, et al. Research on energy saving algorithm of 5G relay cellular network[J]. Telecommunications Science, 2015, 31(3): 55-60.

[4] LI C, ZHU W, YANG L. Optimal energy to spectral-efficiency trade-off in cooperative networks[J]. Wireless Personal Communications, 2015, 80(3): 1-20.

[5] LI C, SUN F, JOHN M, et al. Energy efficient MIMO relay transmissions via joint power allocations[J]. IEEE Transactions on Circuits and Systems-II, 2014, 61(7): 531-535.

[6] LI C, SONG K, LI Y, et al. Energy efficient design for multiuser downlink energy and uplink information transfer in 5G[J].Science China Information Science, 2016, 59(2): 1-8.

[7] MIAO G, HIMAYAT N, LI Y, et al. Energy efficient design in wireless OFDMA[C]//IEEE International Conference on Communications, May 19-23, 2008, Beijing, China. New Jersey:IEEE Press, 2008: 3307-3312.

[8] KIM H S, DANESHRAD B. Energy-constrained link adaptation for MIMO OFDM wireless communication Systems[J].IEEE Transactions on Wireless Communications, 2010, 9(9):2820-2832.

[9] ISHEDEN C, CHONG Z, JORSWIECK E, et al. Framework for link-level energy efficiency optimization with informed transmitter[J]. IEEE Transactions on Wireless Communications,2011, 11(8): 161-176.

[10] 王凯, 张亮, 谭国平. 一种新颖的3D有源天线基站组网波束下倾角选择方法[J]. 电信科学, 2015, 31(1): 90-94.WANG K, ZHANG L, TAN G P. A novel beam downtilt selection method for 3D active antenna system based cellular network[J]. Telecommunications Science, 2015, 31(1): 90-94.

[11] SHI Q J, XU W Q, LI D, et al. On the energy efficiency optimality of OFDMA for SISO-OFDM downlink system[J]. IEEE Communications Letters, 2013, 17(3): 541-544.

[12] ISHEDEN C, FETTWEIS G P. Energy-efficient link adaptation with transmitter CSI[C]//IEEE Wireless Communications and Networking Conference, March 28-31, 2011, Cancun, Mexico.New Jersey: IEEE Press, 2011: 1381-1386.

[13] 3GPP. Study on 3D channel model for LTE: TR36.873,V1.3.0[S]. 2014.

[14] REN Z Y, ZHANG H L, GUO K. A novel method for the improvement of power efficiency in high peak-to-average-power ratio communication systems[J]. Science China Information Sciences, 2010, 53(8): 1697-1702.

[15] ARNOLD O, RICHTER F, FETTWEIS G, et al. Power consumption modeling of different base station types in hetergeneous cellular networks[C]//Future Network and Mobile Summit,June 16-18, 2010, Florence, Italy. New Jersey: IEEE Press,2010: 98-110.

[16] CUI S, GOLDSMITH A J, BAHAI A. Energy-constrained modulation optimization[J]. IEEE Transactions on Wireless Communications, 2005, 4(5): 2349-2360.

[17] ZHANG W, WANG Y, PENG F, et al. Interference coordination with vertical beamforming in 3D MIMO-OFDMA networks[J]. IEEE Comunications Letters, 2014, 18(1): 34-37.

[18] LI Z, CHEN Y, MAI Z. Energy-efficient resource allocation with 3D beamforming in 3D MIMO-OFDMA systems[C]//IEEE International Conference on Communication Software and Networks, June 4-6, 2016, Beijing, China. New Jersey:IEEE Press, 2016: 370-374.

[19] BOYD S, VANDENBERGHE L. Convex optimization[M].Cambridge: Cambridge University Press, 2004.

[20] DAHLMAN E. 3G evolution: HSPA and LTE for mobile broadband[M]. Pittsburgh: Academic Press, 2008.

[21] WU Y, LI X, HEI Y. Downtilts adjustment and power allocation algorithm based on PSO for 3D MIMO systems[C]//IET International Conference on Information and Communications Techologies, April 27-29, 2013, Beijing, China. New Jersey:IEEE Press, 2013: 557-563.

Energy-efficient optimization algorithm based on vertical beamforming for 3D MIMO-OFDMA system

LI Ting, QIU Linjie, JI Wei
School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications, Nanjing 210003, China

An energy-efficient optimization algorithm was proposed for the 3D MIMO-OFDMA communication system. The proposed algorithm based on vertical beamforming technology maximized energy efficiency by adjusting the resource allocation, power allocation and the downtitles of the beam. According to the theory of fractional optimization, the complex fractional optimization problem could be converted into a more tractable integral optimization problem. The lagrangian operator was introduced to obtain the optimal value of energy efficiency by iteration. Simulation results show that the proposed algorithm can achieve higher energy efficiency with fewer iterations.

3D MIMO, vertical beamforming, energy efficiency, fractional optimization theory

s: The National Natural Science Foundation of China (No.61771254, No.61471200), Jiangsu Provincial Natural Science Foundation of China (No.BK20140881), The Horizontal Project of Nanjing University of Posts and Telecommunications(No.2016 Out-of-School 71)

TN929

10.11959/j.issn.1000−0801.2017266

2017−07−02；

2017−09−20

国家自然科学基金资助项目（No.61771254，No.61471200），江苏省自然科学基金资助项目（No.BK20140881），南京邮电大学横向项目（No.2016外71）

李汀（1979−），男，南京邮电大学通信与信息工程学院讲师，主要研究方向为MIMO技术、3D MIMO技术、协作通信等。