水资源监测异常数据模态分解-支持向量机重构方法

张 峰 薛惠锋 WANG Wei 宋晓娜 万 毅

(1.中国航天系统科学与工程研究院研究生部， 北京 100048；2.纽约州立宾汉姆顿大学汤玛士·华生工程与应用科学学院， 宾汉姆顿 NY 13902；3.泰山学院商学院， 泰安 271000； 4.水利部水资源管理中心， 北京 100053)

水资源监测异常数据模态分解-支持向量机重构方法

张 峰1薛惠锋1WANG Wei2宋晓娜3万 毅4

(1.中国航天系统科学与工程研究院研究生部， 北京 100048；2.纽约州立宾汉姆顿大学汤玛士·华生工程与应用科学学院， 宾汉姆顿 NY 13902；3.泰山学院商学院， 泰安 271000； 4.水利部水资源管理中心， 北京 100053)

完备真实的水资源监测数据是支撑数据分析与决策的基本前提。在梳理现阶段水资源监测异常数据的基础上，提出运用移动平均拟合初筛来直观辨识异常监测数据，进而选取集合模态分解对非可直观辨识异常监测数据进行挖掘的方法。将剔除异常监测值后的时序数据作为基于粒子群优化最小二乘支持向量机模型的模拟样本，并利用其恢复所剔除的异常监测数据。对水务公司日取水量监测数据的实证分析结果表明，通过移动平均拟合与模态分解可较大限度地保留含有异常数据的特征向量并实现数据的有效重构，相比传统的统计方法其具有更好的适用性；运用粒子群优化的最小二乘支持向量机可进一步提高对剔除异常值数据的拟合效果，且符合水资源监测数据的季节波动规律特征及对实际取用水状态的客观反映，据此可相对合理地达到恢复所剔除异常监测数据的目的。

水资源监测； 异常数据； 数据重构； 模态分解； 最小二乘支持向量机

引言

实现对水资源的全面监测是国家水资源监控能力建设项目的重点内容，是落实2011年中央一号文件和水利信息化建设的龙头工程，尤其是对8 558个规模以上取用水户、4 493个重要水功能区与入河排污口及737个省界断面等的水量和水质的在线监测，由此逐步形成完善的国家水资源在线监测数据采集传输网络体系，为强化水资源管理提供重要决策支撑[1]。

当前国家水行政部门与相关机构正着力探索处理水资源监测异常数据的有效方法，但水资源监测数据特点不同于传统的统计数据，现有相关数据分析方法的适用性还需要进一步研究。MANDEL等[2]基于水资源分配网络的复杂性，提出采用聚类函数的方法用于挖掘水质异常数据的主要特征及估计未来重大水质事件发生的概率；KAR等[3]针对水资源数据监测中金属污染物的空间变化情况，融合支持向量机与多元回归分析技术，提出了可用于辅助水质远程监测Hyperion数据分类模型；PARK等[4]选取主成分分析方法构建影响水量分配数据变化的关联要素判别模型，并通过测算模型的剩余误差来识别水资源数据的异常值；同样应用主成分的方法，PISINARAS等[5]基于对河流水量与水质的实地调研数据的分析，提出了提高水资源监测数据质量的相关途径；龙秋波等[6]利用中国水利普查数据、水资源统计公报数据等进行数据统计差异分析，并构建了趋势离差和线性回归模型等，分别实现了不同行业之间水资源数据差异甄别与修正；方海泉等[7]选用中位数与集成模态分解技术对水资源监测数据进行分析，并认为根据数据之间的偏差比率可识别其异常值；魏晶茹等[8]针对污水监测数据中存在的数据异常及缺失问题，建立了非线性的支持向量机模型，分别利用拟合误差与样本训练值来完成异常数据的辨识和缺失数据的补充。此外，还有学者探讨了经典统计学中的拉依达准则在水文数据异常值处理中的应用[9]。

综上可知，水资源监测异常数据的识别与处理已成为水资源管理研究工作的重点，而学者们尝试诸多数据建模方法并建立了一定程度的分析基础，但实际上水资源监测数据上传至国家水资源管理系统中具有数据规模大、人工检测操作复杂等特点，同时其数据本身呈现出季节波动规律，此背景下达到有效识别监测异常数据的目标则需要构建与其相适应的检测模型。据此，本文针对日取用水量监测数据为研究对象，结合该类监测数据统计中的实际情况，提出一种基于移动平均拟合和模态分解的水资源监测异常数据检测方法，分别从可直观辨识与非可直观辨识的水资源异常数据处理角度完成其异常数据的辨识，并在验证模型有效性基础上利用粒子群-支持向量机仿真模型实现对异常数据的恢复。

1 水资源监测异常数据情景类别

1.1 可直观辨识异常数据情景

可直观辨识的水资源监测数据异常是指能够利用其监测数据值的变化大小或统计曲线的走势而直接读取的非常规数据状态。按照水资源监测系统呈现出的水资源监测数据状况，以日取水量数据为例，其可直观识别出相对典型的监测数据异常情况有：①数据值连续为零。如图1a所示，水资源监测数据连续一段时间内取水量为零，该情况下多是由于监测设备停用、传感器损坏等问题导致。②数据值连续不变。即水资源监测数据处于非零状态的恒定值(图1b)，正常状态下日取水量均会存在不同程度的差异，但长时间不发生变化则说明其具有产生异常的可能。③数据值突变过大、过低、为零。该情景主要指监测数据在某一点上出现明显的突变，但随后趋于波动不大的连续状态(图1c)，而突变的原因有多种，包括该日取水量确实由于水资源需求而改变，但也可能是设备受外界环境干扰而产生异常波动。④数据值季节性反差。正常状态下日取水量总体上呈一定规律变化，例如观测国家水资源管理系统中对重点取用水户的监测数据值多数是“夏季高而冬季低”的趋势，这主要是由于夏季取用水需求相对较高导致，但局部异常数据则表现出相反态势，即冬季总体水资源需求量相对夏季应下降但所监测的数据却呈持续上升趋势(图1d，其中蓝点表示冬季原始监测数据相对夏季呈现出偏高的异常状态，红点表示正常状态下相对夏季偏低的监测数据状态)，或在夏季出现相反的现象。⑤数据值缺失。该问题存在两种表现形式，即数据连续性缺失与间断性缺失，这两种均为水资源监测系统中无法获取实际监测数据而造成数据值处于空白，但前者是指特定时间段内某一点或连续某几点出现监测数据缺失，而后者则是一套原始数据中存在非连续的2处以上数据缺失，对于上述场景的异常数据重构通常需要与历史年份下该时间段内的监测数据进行拟合与对比进行判定，但是由于目前水资源监控能力尚处于建设阶段，其所能获取的历史年份监测数据相对有限，亟需采用一些定量的方法对其进行重构。

图1 可直观辨识的水资源监测异常数据情景Fig.1 Visual identification of abnormal data scenarios for water resources detection

对于可直观辨识的水资源监测异常数据需要依据实际情况，通过反馈校对的形式检验数据的真伪，若是由实际需求而引发的数据变动则不需再进行调整，而对于由于设备损坏、人工操作等导致的数据异常则需要采取相应的措施进行数据修正。

1.2 非可直观辨识异常数据情景

除上述可直观辨识的异常数据情景外，其它情景多为水资源监测数据连续且上下波动幅度并不明显的情况，但这其中并不能排除全部为监测到的精准数据，通常也会存在通过直接观测而无法轻易发现的数据异常值，对此可将此类异常数据称为非可直观辨识异常数据。据其数据特性来看，非可直观辨识异常数据检测要在看似正常的数据流中查找存在异常的数据点，其判定精度直接关系到水资源监控工作的复杂性，但此类异常数据的排查难度明显高于可直观辨识的异常数据，而这也是自国家水资源监控能力建设以来亟待解决的难点。

1.3 技术路线

基于现有国家水资源监测系统中异常数据的表征状态，本文按照异常数据先检测后重构的思路，确定技术路线如图2所示。

图2 研究技术路线Fig.2 Technical route of research

2 非可直观辨识异常数据检验模型

2.1 概率统计模型

常用经典统计学异常值检测准则有拉依达准则(3σ)、格拉布斯准则、狄克逊准则等[10]，这类准则的使用通常是建立在单次试验重复测量的基础上，但水资源监测数据每日测量重复次数有限，因此这些准则在水资源监测数据异常值辨析的适用性上有待验证。

2.2 模态分解模型

集合经验模态分解(EEMD)是对经典模态分解进行改进的一种融合噪声辅助数据处理方法，在模态分解上具有抗混叠的优势[11]。选取EEMD处理水资源监测异常数据的识别，可有效提取监测数据固有模态函数(Intrinsic mode function，IMF)并挖掘异常特征向量规律[12]，其步骤如下：

(1)对原始时间序列x(t)添加随机高斯白噪声ηm(t)，取得融合噪声后的待处理序列

xm(t)=x(t)+ηm(t)

(1)

(2)将含有白噪声的序列xm(t)进行EMD分解，得到n个IMF分量ci,m(t)(i=1,2,…,n)和剩余分量rn,m(t)。

(3)添加均方根值相等的不同白噪声序列，并反复运行上述步骤，取得M组不同的IMF分量及剩余分量。

(4)计算M组IMF分量与剩余分量的均值，将其最终分解取得的IMF分量与剩余分量定义为模态分解EEMD的分析结果，即

(2)

2.3 粒子群-支持向量机仿真模型

考虑数据样本的规模和最小二乘支持向量机(LSSVM)在解决非线性、规模样本等问题的拟合优势[13]，本文选取该方法对水资源监测异常数据进行恢复。同时，利用粒子群算法(PSO)优化LSSVM核函数的参数。其中LSSVM目标函数为

(3)

式中ω——权向量θ——误差向量

γ——惩罚因子，γgt;0

考虑RBF核函数处理非线性输入与输出关系的适用性，选取其作为LSSVM的核函数[14]

(4)

式中ωi——Lagrange乘子

图3 利用PSO优化LSSVM参数流程Fig.3 Flow chart of parameters of LSSVM optimized by PSO

选取参数优化后的LSSVM模型，将除了存在数据明显异常的水资源监测数据作为模型训练样本进行拟合，通过控制拟合误差辨识其监测数据异常值，进而根据拟合结果对水资源监测异常数据进行恢复。

3 实例分析

3.1 数据说明

以某水务有限公司2016年日取水量监测数据为例(共366 d)，该数据序列源于国家水资源管理系统数据库，记为x(p)(图4)。对其可直观辨识的水资源异常数据初步处理后，重点分析其非可直观辨识的日取水量监测异常数据。

图4 日取水量监测数据变化状态Fig.4 Changing states of daily monitoring water data

3.2 可直观辨识的水资源异常数据粗处理

按照可直观辨识的水资源异常数据的情景类别，观测图4中未出现季节反差的现象，但需对日取水量监测数据的出现数值突变过大、为零、缺失、连续恒定不变的数据点进行初筛，其中数值突变过大包括过高和过低两种情况。对于这类异常数据需要在进行非可直观辨识异常数据分析建模前进行剔除，否则易受其影响而导致所建数据模型判定精度受损，但是同时也要考虑日取水量监测数据信息状态的反映，避免由于数据剔除规模过大而造成数据建模信息支撑不足。据此，鉴于日取水量通常受季节影响相对显著，可分别采用多项式拟合、移动平均算法预估其可直观辨识的水资源异常数据(图5、6，绿色曲线表示多项式与移动平均拟合曲线，红色点指识别的异常数据)。其中，利用多项式与移动平均数据拟合时，可参考经典统计学中的拉依达准则对大于“样本均值±3倍标准差”数据为异常值的定义方法，但同时考虑相比统计类数据，监测类数据具有监测频率高、部分异常值波动幅度大等特点，若直接采用拉依达准则易受异常值影响导致其阈值范围准确度降低。因此，此处采用在剔除样本数据最大值与最小值的基础上计算其数据标准差，进而采用“拟合值±3倍标准差”的方法识别异常数据。其中，拟合值是指运用多项式与移动平均算法在各监测时刻上的拟合数据。

图5 基于多项式的数据拟合曲线与异常点识别Fig.5 Data fitting curve and abnormal point identification based on polynomial

图6 基于移动平均的数据拟合曲线与异常点识别Fig.6 Data fitting curve and abnormal point identification based on moving average

上述多项式拟合可基于数据样本总体对其宏观变动趋势进行反映，具有简单而直观的特点，但通常也易出现过拟合或欠拟合的现象，尤其是在监测数据拟合中对其数据的局部波动规律拟合不足；而移动平均法则不仅对原始监测数据具有修匀或平滑的作用，而且同时还可以在一定程度上融合原有时序数据的波动特点，但无法实现对波动幅度并非异常明显数据的检验。根据数据离散状态，可知多项式拟合状态下需要剔除的异常数据点相对较多(41项)，而经实际校验反馈发现其中部分数据点被误判为异常值。采用移动平均法所需剔除异常数据点为14项，其拟合的数据波动规律要比多项式拟合效果相对更加显著。而对比两种方法监测出的异常数据量，多项式拟合要远高于移动平均法，这主要是因为移动平均法能够在不改变原始监测时序数据趋势的情况下，可对局部监测数据的变动规律进行较高程度的拟合，并体现其局部波动状态，多项式拟合难以实现该功能，而对于移动平均法无法检测出的非可直观辨识异常数据则可通过EEMD方法进行进一步挖掘。因此，在保障数据建模信息尽可能完整的前提下，选取移动平均法作出的可直观辨识的水资源异常数据更加合理，剔除这类异常数据点后的日取水量监测数据序列记为x(p′)，其曲线如图7所示。

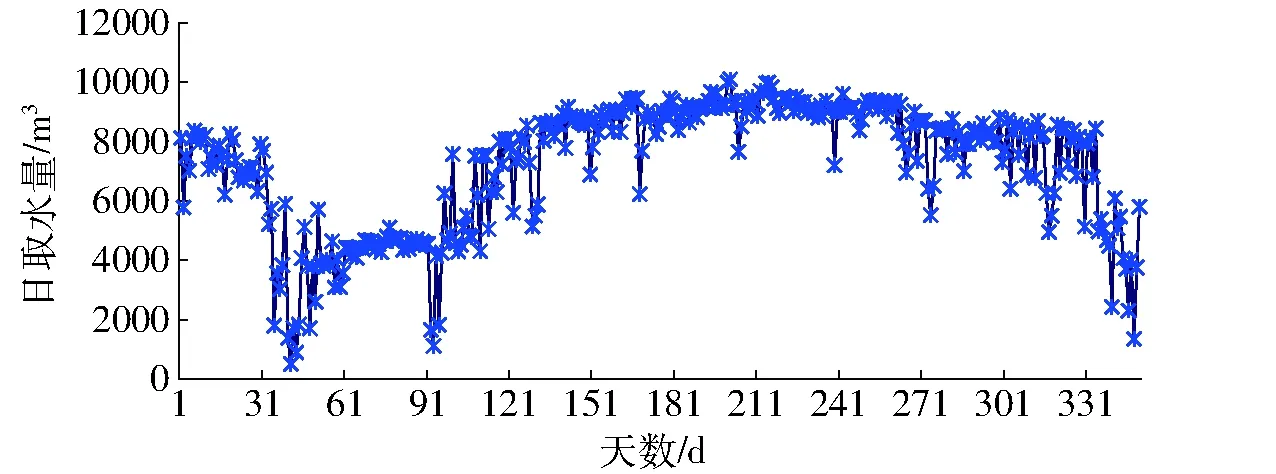
图7 剔除可直观辨识异常点后监测数据Fig.7 Daily monitoring water data after abnormal data revised

3.3 基于模态分解的非可直观辨识异常数据分析

以初步修正后的时间序列x(p′)为样本，在维持其数据点时序位置不变的情况下采取EEMD模型分解其样本数据，如图8所示。其中包括8组分量，7个固有模态函数ci(i=1,2,…,7)与1个残余项r。观测其分量可知c1整体均呈高频噪声状态，而c2局部数据噪声较为显著，考虑监测数据中突变型异常数据的特征，其异常数据通常可引发局部监测值发生相对显著的时序波动，表现于模态分量中为高频噪声，因此，要取得相对稳定的整体原始监测数据与局部变动态势，则可对高频分量进行剔除处理，并利用剩余低频分量实现对原x(p′)数据序列的滤波处理。因此，可将后6项相对低频分量进行数组重构，记为x(p″)，如图9所示。按照重构结果，可发现重构数据序列x(p″)能够对样本中的多数正常数据进行较高精度拟合，并取得了相对较为平缓的重构数据趋势线，即满足对数据变化特征客观反映的标准。

图8 非可直观辨识异常数据模态分解Fig.8 Daily monitoring water data analysis by EEMD method

图9 模态分解重构数据拟合状态Fig.9 Data reconstruction based on EEMD method

图10 相对误差计算结果Fig.10 Results of relative error calculation

图11 全部异常数据检测结果Fig.11 Results of all abnormal data detection

为进一步提高基于模态分解重构数据与粗处理后监测原始数据的对比程度，需测算数据序列之间的相对误差E_p，结果见图10。按照相对误差E_p阈值±0.5的控制标准(该阈值根据现有水资源监测数据统计分析和相关专家经验初步设定，随着其监测数据历史样本的增加可进一步优化)，设定当|E_p|大于0.5时，其所对应的x(p″)数据点判定为异常值。据此，发现其中有11项监测数据出现异常状态。而为增强异常数据在水资源管理系统中的可视化水平，则结合可直观辨识的日取水量异常数据粗处理结果，将整个步骤中判定为异常数据(含可直观辨识与非可直观辨识异常数据)点处均设为零，记为x(p‴)，如图11所示。由图11可看出，出现异常数据的时间多集中于上半年，而下半年则相对较少，说明随着水资源监测体系与水资源监控管理信息平台建设的不断完善，对水资源监测数据采集与传输精准度的提升有了显著性改善。而局部水资源监测异常数据表明，部分监测还存在数据连续性异常的现象，特别是在132～137 d期间，数据呈连续为零的状态，而此类问题的多数情况下是由监测设备本身或受环境影响而导致，即说明在整体水资源监测水平上升的良性趋势下，局部监测基础设施仍需完善。

为验证本文提出的水资源监测异常数据检验方法的有效性，同时采用了经典统计学中的3σ准则和箱线图方法对其数据进行异常分析[18]，以增加对比度。由于这类统计方法适用的条件存在差异，且缺乏对水资源监测数据时序特征的考虑，结果发现在依据3σ准则下，其正常阈值范围为[-1 299.56, 15 510.83]，即仅有3个数据异常点可被识别；而选取箱线图统计中，也只有4个异常点被检验出来(图12)，多数异常值被忽略，无法为水资源监测数据分析与决策提供足够的信息支撑。而该对比结果也进一步印证了本文所采用的异常值检测模型对水资源监测数据具有实用性。

图12 基于箱线图异常值检测结果Fig.12 Abnormal data detection based on box-plot

3.4 基于PSO-LSSVM的异常数据恢复

ij=(xij-xjmax)/(xjmax-xjmin)

(5)

xj——xij所在j列数值

xij——原始监测数据

xjmax——xj的最大值

xjmin——xj的最小值

利用RBF核函数，根据模型(4)对数据序列ϑ_p分别进行LSSVM、PSO-LSSVM模型样本训练，并通过PSO-LSSVM拟合模型重构图11中检测出的异常数据点，结果如图13与图14所示，而图15显示了粒子群进化中适应度的变化情况。

图13 基于序列ϑ_p的PSO-LSSVM数据模拟Fig.13 PSO-LSSVM sample training based on ϑ_p

图14 基于PSO-LSSVM的异常数据恢复Fig.14 Recovery of abnormal data based on PSO-LSSVM

图15 粒子群进化与适应度变化曲线Fig.15 Evolution and fitness of particle swarm

图16 基于曲线拟合的异常数据恢复Fig.16 Recovery of abnormal data based on curve fitting

3.5 讨论

(1)在国家水资源监控能力二期建设的关键阶段，如何对现有规模性水资源监测数据进行全面分析，进而为水资源管理决策提供有效支撑是亟需解决的重要问题，而实现数据分析决策支持的前提是提高数据的可用性，尤其是水资源监测数据完备构建与真伪鉴定，这类问题与水资源监测异常数据紧密相关。然而现阶段相关部门及学术研究中对水资源监测异常数据并没有形成统一的认识[19-20]，在实际水资源统计与监测数据管理中，通常认为异常值是偏离邻近监测值较大的数据。据此，本文所定义的水资源监测异常数据是出现数值连续不变、数值呈季节性反差，以及数据相比邻域时刻呈现突变过大、过低或为零等的非常规数据。该定义方式基本符合水资源监测数据管理中的实际状况，也可对相关监测数据分析提供借鉴。

(2)基于维持水资源监测异常数据的实际特征而采取的移动平均拟合与EEMD方法识别日取水量监测异常数据的研究思路，能够较大程度地模拟监测点的水资源取用状态及变动趋势。实际上，导致水资源监测数据异常的因素有很多，但是归结起来可分为两大类，即实际突变异常和待修正异常。其中实际突变异常主要是指由于实际取用水需求改变而引发的监测数据上升或下降，而待修正异常则是受监测设备或环境等影响而造成实际数据与水资源管理系统中呈现的数据存在较大差异。对于前者可通过人工校对识别，并保留其原始监测数据，而后者则需运用相应的方法或模型进行辨识，而本文提出方法可为其提供一种数据分析方法。此外，运用PSO-LSSVM的日取水量监测数据拟合曲线与监测点取用水实际状况相一致，且符合季节波动规律，这不仅可用于解决监测异常数据的恢复，也适用于监测数据缺失填补的情况。

4 结束语

按照可直观辨识与非可直观辨识的异常值识别思路对水资源监测异常数据存在情况进行总结梳理，在其基础上提出了基于移动平均拟合与EEMD相结合的水资源监测异常数据检测模型，和基于PSO-LSSVM的异常数据恢复方法，并通过对水务公司的实际日取水量监测数据进行实证分析，验证了上述方法在处理其监测异常数据上的可行性与有效性。研究发现，传统的统计手段难以满足监测频率高同时具有季节周期波动规律的水资源监测数据分析的要求，而经过对可直观辨识的异常数据进行粗处理后，采用EEMD方法可在保障其监测数据时序特征状态不变的情况下完成对异常数据的筛选，其适用性更强。同时，PSO优化后的LSSVM模型可更加系统地拟合剔除异常数据后的样本，其拟合状态与实际取用水季节波动规律基本一致。因此，该类监测异常数据处理方法可为水行政部门推进水资源监控能力建设提供理论支持，也能对其它相关领域的时序监测数据分析提供参考。

1 中华人民共和国水利部,财政部.国家水资源监控能力建设项目实施方案(2012—2014)[S].北京: 中华人民共和国水利部,2012.

2 MANDEL P, MAUREL M, CHENU D. Better understanding of water quality evolution in water distribution networks using data clustering[J]. Water Research, 2015, 87: 69-78.

3 KAR S, RATHORE V S, SHARMA R, et al. Classification of river water pollution using Hyperion data[J]. Journal of Hydrology, 2016, 537: 221-233.

4 PARK S, JUNG S Y. Principal component analysis of water pipe flow data[J]. Procedia Engineering, 2014, 89: 395-400.

5 PISINARAS V, PETALAS C, GEMITZI A, et al. Water quantity and quality monitoring of Kosynthos river, north-eastern Greece[J]. Global Nest Journal, 2007, 9(3): 259-268.

6 龙秋波,贾绍凤,汪党献.中国用水数据统计差异分析[J].资源科学, 2016, 38(2): 248-254.

LONG Qiubo, JIA Shaofeng, WANG Dangxian. Disparity in China’s water use statistics[J].Resources Science, 2016, 38(2): 248-254. (in Chinese)

7 方海泉,薛惠锋,蒋云钟,等.基于EEMD的水资源监测数据异常值检测与校正[J/OL].农业机械学报, 2017，48(9)：257-263. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1amp;file_no=20170932amp;journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2017.09.032.

FANG Haiquan, XUE Huifeng, JIANG Yunzhong, et al. Outlier detection and correction for water resources monitoring data based on EEMD[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017，48(9)：257-263. (in Chinese)

8 魏晶茹,马瑜,白冰,等.基于PSO-SVM算法的环境监测数据异常检测和缺失补全[J].环境监测管理与技术, 2016, 28(4): 53-56.

WEI Jingru, MA Yu, BAI Bing, et al. Anomaly detection and missing completion of environment monitoring data based on PSO-SVM[J]. The Administration and Technique of Environmental Monitoring, 2016, 28(4): 53-56. (in Chinese)

9 侍建国,张亦飞.拉依达准则在处理区域水文数据异常值中的应用[J].海河水利, 2016(5): 49-51.

SHI Jianguo, ZHANG Yifei. The application of Pauta criterion in regional hydrological outlier analysis[J]. Haihe Water Resources, 2016(5): 49-51. (in Chinese)

10 ANDERSON T W, ANDERSON T W, ANDERSON T W, et al. An introduction to multivariate statistical analysis[M]. New York: Wiley, 1958: 30-36.

11 曾祥,周晓军,杨辰龙,等.基于经验模态分解和S变换的缺陷超声回波检测方法[J/OL].农业机械学报,2016,47(11):414-420.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20161156amp;flag=1. DOI：10.6041/j.issn.1000-1298.2016.11.056.

ZENG Xiang, ZHOU Xiaojun, YANG Chenlong, et al. Ultrasonic defect echoes identification based on empirical mode decomposition and stransform[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(11):414-420. (in Chinese)

12 WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

13 SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300.

14 DEMPE S, ZEMKOHO A B. On the Karush-Kuhn-Tucker reformulation of the bilevel optimization problem[J]. Nonlinear Analysis: Theory, Methods amp; Applications, 2012, 75(3): 1202-1218.

15 GORJAEI R G, SONGOLZADEH R, TORKAMAN M, et al. A novel PSO-LSSVM model for predicting liquid rate of two phase flow through wellhead chokes[J]. Journal of Natural Gas Science and Engineering, 2015, 24: 228-237.

16 YANG X, YU F, PEDRYCZ W. Long-term forecasting of time series based on linear fuzzy information granules and fuzzy inference system[J]. International Journal of Approximate Reasoning, 2017, 81: 1-27.

17 SUBASI A. Classification of EMG signals using PSO optimized SVM for diagnosis of neuromuscular disorders[J]. Computers in Biology and Medicine, 2013, 43(5): 576-586.

18 KOSE E, TOKATLI C, ÇICEK A. Monitoring stream water quality: a statistical evaluation[J]. Polish Journal of Environmental Studies, 2014, 23(5): 1637-1647.

19 BARNETT V, LEWIS T. Outliers in statistical data[M]. New York: Wiley, 1994： 12-20.

20 FILZMOSER P. Identification of multivariate outliers: a performance study[J]. Austrian Journal of Statistics, 2016, 34(2): 127-138.

MethodsofAbnormalDataDetectionandRecoveryforWaterResourcesMonitoringBasedonEEMDandPSO-LSSVM

ZHANG Feng1XUE Huifeng1WANG Wei2SONG Xiaona3WAN Yi4

(1.GraduateSchool,ChinaAcademyofAerospaceSystemScientificandEngineering,Beijing100048,China2.ThomasJ.WatsonSchoolofEngineeringandAppliedScience,BinghamtonUniversity,StateUniversityofNewYork,BinghamtonNY13902,USA3.SchoolofBusiness,TaishanUniversity,Taian271000,China4.WaterResourcesManagementCenter,MinistryofWaterResources,Beijing100053,China)

The national water resources monitoring capacity building project which started in 2012 in China is an important way to improve the level of water conservancy information. It requires that the historical time-series monitoring data of water resources should be complete and reliable so that it can be used to support data analysis and decision making. The basic scenarios for monitoring abnormal data were summed up and a comprehensive model was proposed, aiming at abnormal data detection and recovery. Moving average fitting and ensemble empirical mode decomposition (EEMD) method were introduced to identify both observable and non-observable abnormal monitoring data. The particle swarm optimization based least squares support vector machine (PSO-LSSVM) was then adopted for abnormal data recovery and imputation. All above methods were tested with the daily water consumption monitoring data of water company. Results showed that the feature vector that contained exception data could be well preserved by moving average fitting and EEDM method and the effective reconstruction of water monitoring data was achieved, exhibiting better applicability than traditional statistical methods. Moreover, it can be observed that the PSO-LSSVM model had the ability to further improve the fitting results of the time-series data that excluded outliers. The fitted curve conformed to the seasonal fluctuation rule and it was consistent with the actual state of water demand. Accordingly, the objective of recovering the excluded data exception could be achieved reasonably by using this method. Furthermore, these methods can be applied to the analysis of monitoring data in other areas.

water resources monitoring; abnormal data; data reconstruction; modal decomposition; least squares support vector machine

10.6041/j.issn.1000-1298.2017.11.038

N945.2

A

1000-1298(2017)11-0316-08

2017-08-15

2017-09-07

国家自然科学基金委员会-广东联合基金项目(U1501253)和广东省省级科技计划项目(2016B010127005)

张峰(1989—)，男，博士生，主要从事系统工程与工业工程研究，E-mail: aerospace1989@163.com