真空预压加固吹填土地基的三维有限元分析

吴灵军

摘要：通过疏浚吹填的方式进行大面积围海造陆是解决城市土地资源日益紧缺的有效途径。本文在真空联合覆水预压法加固处理疏浚吹填地基的实际工程基础上，根据抽真空期间现场实时观测的数据，结合三维Biot固结理论采用修正剑桥本构模型，使用ABAQUS软件进行三维有限元模拟计算，结果表明模拟计算结果与现场实测数据曲线拟合较好。

Abstract： It is an effective way to solve the increasingly scarce urban land resources by making a large area of land reclamation through dredging and filling. Based on the actual engineering of dredging and dredging foundation under vacuum combined with water preloading method， based on the real-time observation data of vacuum period， combined with three-dimensional Biot consolidation theory， the modified Cambridge constitutive model is used， and ABAQUS software is used to carry out three-dimensional FEM simulation. The results show that the simulation results are in good agreement with the measured data.

关键词：吹填土；真空预压；固结沉降

Key words： reclaimed soil；vacuum preloading；consolidation settlement

中图分类号：TU472.3+3 文献标识码：A 文章编号：1006-4311（2017）36-0126-03

0 引言

真空预压法因设备简单、操作方便、加固面积大、能源消耗少、加固效果好、预压时间短、无环境污染等显著优点，使得在疏浚吹填围海造陆工程中得到广泛的应用。在围海造陆过程中，将淤泥泥浆经水力吹填至天然地基上达到标高后形成吹填土地基，然后铺设砂垫层向地基中按一定间距施打竖直塑料排水板，吹填土地基中的超孔隙水压力在真空预压过程中快速消散[1]，土体加速产生压缩固结[2]，致使地基承载力得以加强。

在目前的塑料排水板地基固结常规计算方法中，一般以单个塑料排水板或砂井地基转换为砂墙地基，考虑在真空预压施工过程中对周边土体产生的涂抹效应和井阻作用，将轴对称单井问题等效转换为平面应变砂墙间固结度的问题[3-4]，依据太沙基固结理论或Biot固结理论求得数值解法[5]，如1989年，谢康和，曾国熙[6]推出考虑涂抹效应影响、井阻作用下的砂井地基解析解，并取得了等应变条件下较为全面的解析理论。赵维炳等[7]通过研究平面应变条件下砂井地基双向渗流等应变固结理论解，得出砂井地基平面应变情况和轴对称情况之间的等效公式。由于此种方法的计算复杂性及依于非严格的Biot固结理论，按固结度等效原则进行变换后，各点的几何位置不能和原型相对应，且只能較好地计算表面沉降，而对孔压、横向应变等计算结果并不理想，有限元法却可以有效地对整个地基固结变形进行真实的分析计算。

实际上真空预压作用下的排水板（竖井）地基属于三维固结问题，较为理想的做法是采用三维有限元进行计算，但若将塑料排水板或砂井视作实体单元进行划分，会致使单元体节点位移分量和孔压的未知量过多，分析计算规模太大，采用三维Biot固结理论对砂井地基进行分析有一定的限制性。目前对三维变形-渗流有限元计算的研究并不多见，如王旭升等[8]基于对称性原理和Biot固结理论，对三维渗流和二维变形的有限单元法进行了改良，将砂井地基有效合理地进行了三维剖分，得到比较理想的方案，使PDSS模型能直接应用在呈正三角形布置的砂井中；董志良[3]等依于固结度等效的原则，建议考虑涂抹效应影响对土体渗透性存在的弱化效应并作相应的处理，从而减小工作量，构造三维有限元模型对真空覆水预压施工过程进行模拟分析；邓岳保，谢康和等[9]在经典Biot固结理论基础上引入Hansbo非达西定律，应用加权残数法推出三维有限元方程，且通过编写非达西渗流模块对有限元方程组进行求解。

本文将真空预压塑料排水板视为线弹性单元，考虑涂抹效应影响并采用修正剑桥本构模型，基于三维Biot固结理论，利用abaqus软件结合实际工程构建三维有限元模型进行模拟计算。

1 三维有限元模型建立

1.1 Biot三维固结有限元方程

基于三维Biot固结理论，对吹填土地基进行有限元分析。依据谢康和[10]推导的固结方程，考虑应力边界和流速边界条件，对三维Biot固结方程进行空间、时间离散后求得Biot三维固结有限元方程：

■ k'k' T ■δβ=RS（1）

[■]和[k']分别由单元矩阵[■]和[k']中的元素叠加而成

δ、β分别为位移和超静孔压值，{S}=[k']T{δt-Δt}。

1.2 修正剑桥模型

土体作为一种三相结构材料，具有比较强的非线性特征，而Duncan-Chang模型可以很好地反映应力与应变之间的非线性关系及土体的弹塑性变形，该模型对参数的变化情况积累了较为丰富的经验，在岩土工程非线性模型中Duncan-Chang模型成为具有代表性且应用比较广泛的本构模型[11-12]。Duncan-Chang基于常规三轴试验由广义胡克定律和摩尔库伦准则推导出以切线弹性模量Et来表示增量胡克定律中的弹性模量的表达式[13]：endprint

Et=KEpa■■1-■■（2）

式（2）表示Et随应力水平增加而降低，随固结压力增加增加而增加。式中：

c、φ为粘聚力和内摩擦角，pa为大气压，Rf为破坏比，KE为模量系数，σ1、σ3为最大、最小主应力。

1.3 涂抹区的处理

真空预压塑料排水板打设过程中会对周围土体产生扰动，即在排水板表面附近形成涂抹区，这种涂抹效应使处于涂抹作用区范围内土体的渗透性降低即单井的水平向渗流系数变小，从而导致固结速率的减小[2]。陈小丹，赵维炳[14]基于固结度或平均孔压相等的条件下将三维砂井固结问题转化为简单的平面问题，推导出等效公式，谢康和等[6]针对等应变条件下经典Barron理论和Hansbo理论中存在的不足之处，考虑井阻和涂抹影响，推导出满足径向固结基本方程及所有求解条件的精准解，得出了较为全面的砂井固结理论。陈平山等[2]在谢康和的径向固结精确解的基础上通过对涂抹效应的均质化处理，推导出涂抹效应均化到影响区土体的径向渗透系数表达式，并结合算例将三维有限元计算解与解析解进行比较，验得该方法的精确性与可行性。

本文采用文献[2]中的方法计算径向渗透系数，即：

k■■=■kh

其中：

F■■=lnn-■■+■1-■

Fa=ln■+■lns-■

2 工程应用

利用自定义塑料排水板单元及编制的三维Biot固结理论有限元程序分别对真空预压加固的吹填土地基进行计算对比。

2.1 工程概况

广州港某吹填软基真空联合覆水预压工程，该区总处理面积约103.4万m2，共划分为34个加固区，其中试验区为200m×160m范围的长方形，处理区为机械水力吹填而成的超软地基，吹填层厚度为5.4m。塑料排水板呈正方形布设，间距1m，打设深度20m。膜上堆载1m深的水预压。场区地层自上而下分别为：第一层为砂垫层，层厚为1m；第二层为吹填土，层厚为5.4m；第三层为淤泥，层厚为16m；第四层为淤泥质土，层厚为6.7m；第五层为粉细砂，层厚为2.3m；第六层为粉质粘土，层厚为1.6m。场区真空预压恒载约85天，抽真空期间膜下真空度维持在85kPa以上。

2.2 有限元计算模型

砂垫层采用摩尔库伦模型，地基土采用修正剑桥模型。考虑对称性，本文取加固区长宽一半即长度100m，宽度80m，影响区范围取加固区外80m，深度为33m，即三维模型尺寸为180m×160m×33m，如图1所示。

真空预压塑料排水板界面尺寸100mm×4mm，按面积等效原则，将排水板界面尺寸等效为0.02m×0.02m的正方形进行分析。为减少由于网格划分过密带来的庞大计算量及网格划分过疏产生的计算精度不足等问题，本文将竖向塑料排水板的间距扩为4m。单元类型为C3D8P，共 204800节点，216513个单元。

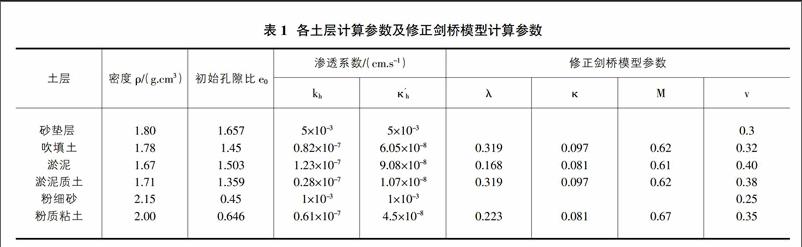
根据现场监测成果和加固前后室内土工试验，得出各土层物理力學参数和修正剑桥模型计算参数如表1所示。

2.3 边界条件

①位移边界：模型四周竖向边界设为不透水边界即约束模型左右两侧水平两方向位移，竖向位移不约束，固定模型底边水平和竖向所有位移。

②孔压边界：加固区地表面所有节点的孔隙水压力为-85kPa（负的真空压力），影响区地表面孔隙水压力为0。

3 计算结果分析

3.1 表面沉降

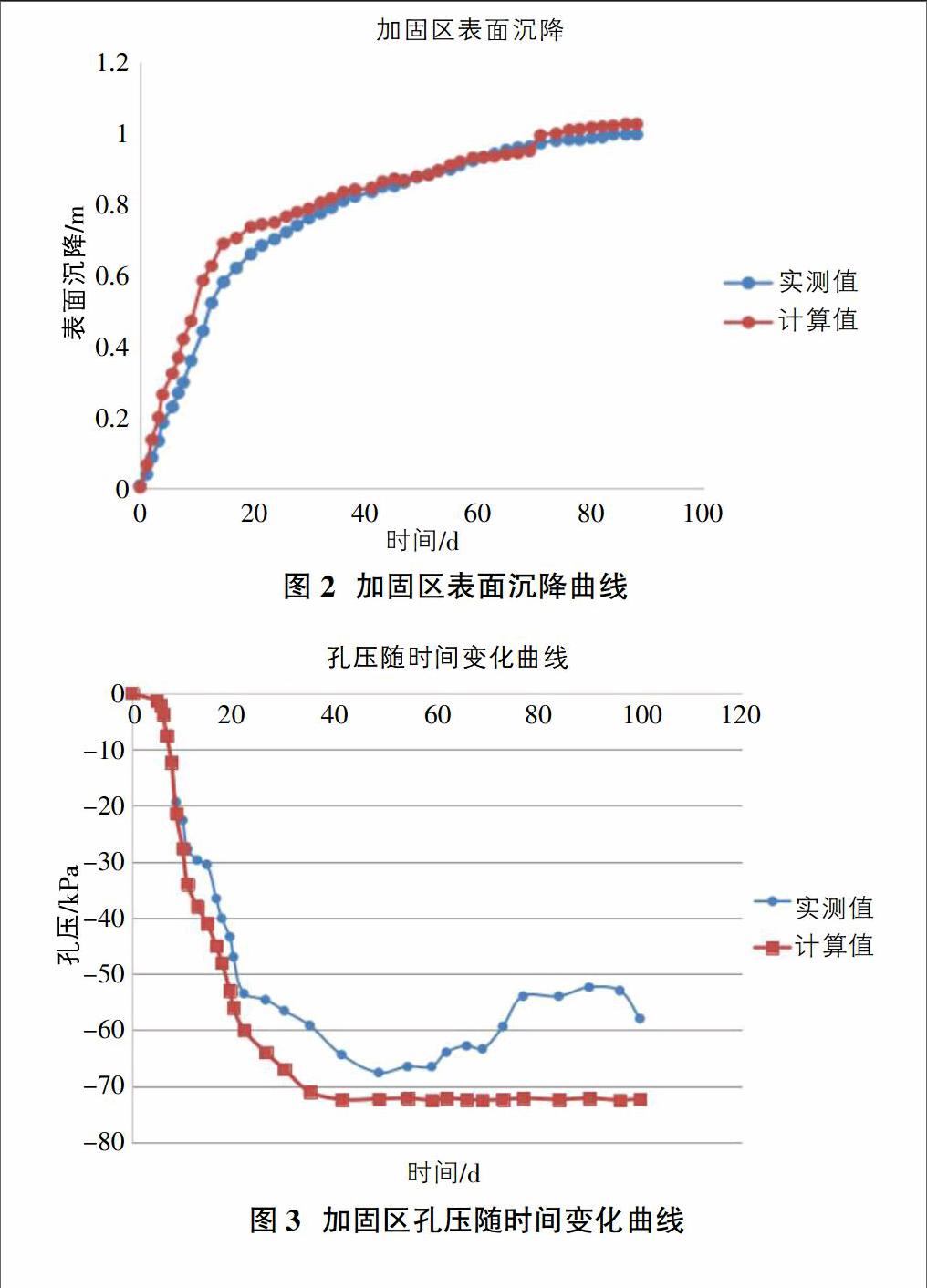
图2为表面沉降数值模拟计算结果和实测结果与时间的关系，对比分析可知，在初始阶段40d内数值模拟计算结果要大于实测结果，在15d左右差值达到最大，原因可能在于模拟条件状况、本构模型及参数与现场施工和土层地质情况存在差异，40d后计算值与实测值笔记趋于接近，总的模拟计算和实测结果趋势拟合比较好。真空预压阶段由于孔隙水压力的快速消散和有效应力的增加，土体沉降速率相应比较高，沉降量也比较大。

3.2 孔隙水压力

图3为真空覆水预压100天内加固区孔隙水压力随时间变化曲线，从图可知，在真空预压前期模拟计算结果与实测结果比较相近，20d后实测数据波动性较大，而计算数据相对比较连续顺滑，模拟计算值与实测值的差值拉大；原因在于，打设排水板抽真空开始后土层中的孔隙水压力消散速率较快，随着孔隙水压力进一步消散降低直至稳定，各土层产生压缩固结；抽真空期间所测得的孔压为负值，表明加固区地基趋于安全稳定，当收到外界如台风等因素影响时孔隙水压力数据波动比较明显。

4 结论与建议

基于三维Biot固结理论，考虑砂井的涂抹效应影响，对各土层渗透系数进行均质化处理，使用修正剑桥本构模型进行三维有限元模拟。结论如下：

①三维有限元可以很好地模拟真空预压期间的压缩固结，据图比照可知模拟计算结果与现场实测数据曲线拟合较好，修正剑桥模型和弹性模型在模拟计算实际工程中可以得到很好的应用。

②真空联合覆水预压法使土层中的孔隙水压力得以快速的消散，从而产生很好的压缩固结效果，有效地消除了主固结沉降及减小了工后沉降。

参考文献：

[1]孙立强，闫澍旺，何洪娟，李伟.吹填土地基真空预压加固过程分析及有限元研究[J].岩土工程学报，2010，29（9）：3879-3884.

[2]陈平山，房营光，莫海鸿，张功新，董志良.真空预压法加固软基三维有限元计算[J].岩土工程学报，2009，31（4）：565-570.

[3]董志良，陈平山，莫海鸿，张功新.真空预压法有限元计算比较[J].岩石力学与工程学报，2008，27（11）：2348-2353.

[4]陈立宏，陈祖煜，李广信.砂井地基有限元计算的等效平面应变法[J].土木工程学报，2004，37（6）：83-87.

[5]沈珠江，陆舜英.软土地基真空排水预压的固结变形分析[J].岩土工程学报，1986，8（3）：7-15.

[6]谢康和，曾国熙.等应变条件下的砂井地基固结解析理论[J].岩土工程学报，1989，11（3）：4-17.

[7]赵维炳，陈永辉，龚友平.平面应变有限元分析中砂井的处理办法[J].水力学报，1998，10（6）：53-77.

[8]王旭升，陈崇希.砂井地基固结的三维有限元模型及应用[J].岩土力学，2004，25（1）：94-98.

[9]邓岳保，谢康和.考虑非达西渗流的比奥固结有限元分析[J].岩土工程学报，2012，34（11）：2059-2065.

[10]谢康和，周健.岩土工程有限元分析理论与应用[M].科学出版社，2002.

[11]陈育民，刘汉龙.邓肯-张本构模型在FLAC3D中的开发与实现[J].岩土力学，2007，28（10）：2123-2126.

[12]朱百里，等.计算土力学[M].上海科学技术出版社，1990，08.

[13]钱家欢，殷宗泽，等.土工原理与计算[M].中国水利水电出版社，1996，05.

[14]陈小丹，赵维炳，等.考虑井阻和涂抹的砂井地基平面应变等效方法分析[J].岩土力学，2005，26（4）：567-571.endprint