双级矩阵变换器的解析变换及仿真

王 丹，翟玉千

（1.西安铁路职业技术学院电气工程系，陕西西安710014；2中国北车唐山轨道客车有限责任公司河北唐山064000）

双级矩阵变换器的解析变换及仿真

王 丹1，翟玉千2

（1.西安铁路职业技术学院电气工程系，陕西西安710014；2中国北车唐山轨道客车有限责任公司河北唐山064000）

为了优化双级矩阵变换器输出性能，提高其电压利用率，本文在分析双级矩阵变换器的拓扑结构的基础上，提出在整流级采用有零矢量的空间矢量调制策略；在新的调制策略的思想下，通过对整流级和逆变级的解析变换，推导出其开关函数。通过仿真得到输出直流局部平均电压恒定，电压利用率达到86.6%，验证了该调制策略的正确性和可行性。

双级矩阵变换器；整流级有零矢量；开关函数；仿真

双级矩阵变换器以其良好的输入输出性能、能量双向流动、功率开关器件少、换流方便和控制复杂度低等优点而成为近年来研究的热点[1-2]。双级矩阵变换器由双向开关的交-直整流电路和普通直-交逆变电路两个部分组成[3-4]，基于传统矩阵变换器间接传递函数原理。

目前，整流级的调制策略主要采用整流级无零矢量的调制策略，该策略能够保证优良的输入输出性能，较高的电压利用率[5-6]，但是需要修正逆变级的调制系数，逆变级的调制相对复杂。本文正是针对这一问题而进行研究。

1 调制策略分析

以18开关双级矩阵变换器的拓扑结构来分析双级矩阵变换器的调制原理。图1所示。

设三相电源电压为正弦且平衡的前提下，输入的电压可表示为[7]:

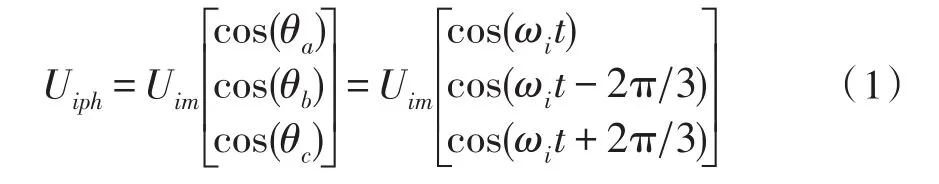
式中：ωi为输入电压角频率，Uim为输入电压幅值。

如图2所示整流级中的6个双向开关可以合成6个输入相电流的非零空间矢量i1-i6，a、b、c三相双向开关导通状态分别用图中括号里的数字来表示，“1”表示与p极相连接的双向开关导通，“0”表示与n极相连接的双向开关导通，“X”表示所在相上下桥臂的双向开关均处于关断的状态。当整流级某一相上下桥臂的双向开关均导通，另外两相桥臂的双向开关都关断的状态时，输入电流矢量即为零矢量，整流级输出的直流电压为零。

图1 双级矩阵变换器的拓扑结构图

图2 整流级有零矢量调制

任意时刻的输入相电流空间矢量Ii，由其所在扇区相邻的两个开关矢量iμ、iv以及一个零矢量i0合成。dμ、dv及d0c分别表示iμ、iv和i0的开关占空比[8]，则

由空间矢量和正弦定理可得，开关矢量的占空比计算公式为：

式中，θsc为扇区角；Tμ、Tv、T0c分别表示iμ、iv、i0在采样周期中的作用时间；mc为输入相电流空间矢量调制系数，且0≤mc≤1。可以改变输入相位差ϕi来调节输入功率因数，当φi=0∘时，功率因数为1。

逆变级的调制中，通过空间矢量调制和正弦定理计算得出为：

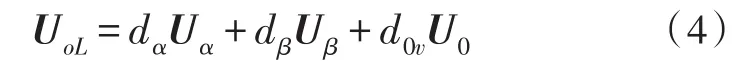
其占空比分别为：

式中，θsv为输出线电压的扇区角。Ts为开关的采样周期；Tα、Tβ、T0v为开关的导通时间；dα、dβ、d0v为开关导通的占空比；mv表示输出线电压的调制系数，是一个常量，不需要修正且有

2 解析变换

2.1 整流级解析变换

如图2所示合成的参考输入电流矢量位于第一扇区，可以得出一个调制周期内直流平均电压值用矩阵的表示为：

根据第一扇区的开关状态，整流级的三相输入电流值为：

其中，Trec为整流级输入输出电压和电流之间的变换关系，称之为整流级在第一扇区占空比形式的调制矩阵[9]。式（9）：

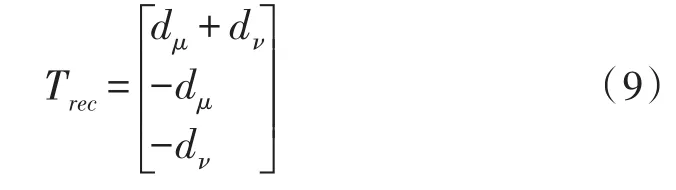
同理可以求出其他各个扇区所对应的占空比形式的变换矩阵。

假设φi为输入端电压和电流之间的相位差，ωi为输入电压角频率，那么整流级第一扇区占空比形式的调制矩阵所对应的开关传递函数为[5]：

同理，在各个扇区中θsc=ωit-φi+30∘-(k-1)60o（k为扇区编号），得到的各个扇区占空比的调制矩阵的开关传递函数与式10具有相同的形式，所以将其称为整流级通用的开关传递函数，简称为整流级开关函数[9]。

2.2 逆变级解析变换

设逆变级输出线电压矢量位于第一扇区[5]，根据非零电压矢量的开关状态，其三相输出线电压在一个调制周期内的平均值为[10]：

对应一个调制周期内直流电流的平均值为：

式中，Io为逆变级输出的相电流，Tinv表示逆变级输入输出电压和电流之间的变换关系，称为逆变级在第一扇区占空比形式的变换矩阵[11-16]。为：

同理可以求出其他各个扇区所对应的占空比形式的变换矩阵。

设ωo为输出电压的角频率，ϕo为输出线电压的初始相位角，第一扇区占空比形式的调制矩阵所对应的开关传递函数为：

同理，在各个扇区中θsv=ωot-ϕo+60∘-(j-1)60∘（j为扇区的编号），各个扇区占空比的调制矩阵的开关传递函数与式14具有相同的形式，所以把式14称为逆变级通用的开关传递函数，简称为逆变级开关函数。

2.3 总解析变换

由式（7）和式（11）联立，可得：

式中，T称为双级矩阵变换器总的开关函数，m=mc·mv称为双级矩阵变换器总的调制系数，即电压增益控制变量，且0≤m≤1。

由式（1）、式（7）和式（10）联立，可得：

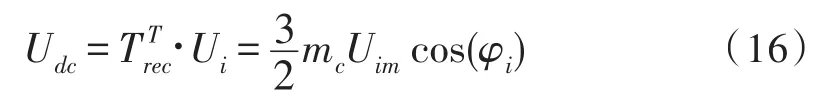
当输入电压的幅值、整流级调制系数和输入功率因数角恒定的情形下，Udc是一个恒量。

由式（12）、式（14）和式（16），可以求得输出线电压：

由式（18）可知，当m=1且φi=0时，可得最大的电压传输比。

采用整流级有零空间矢量调制方法是通过开关函数直接计算占空比，使计算大大简化；并通过两级开关函数的参考电压直接控制输入电流和输出电压，保证了良好的输入输出性能；而采用该调制方法能使双级矩阵变换器的电压利用率最高可达到86.6%。

3 仿真研究

仿真模型主要组成部分及参数如下：三相对称电源输入，其相电压幅值为Uim=220 V，频率为f=50 Hz；由理想开关构成的整流级和逆变级模块；驱动控制模块（参考电压和S函数模块）；输入滤波模块LC滤波器，滤波电感L=5.5 mH，滤波电容C=70μF；负载为三相对称阻感性负载，每相电阻R=5Ω，每相电感L=5 mH；PWM周期为T=0.1 ms，仿真算法为ode15S。

整流级的参考电压幅值为1，角频率为314 Hz，初相角为0°；逆变级的参考电压幅值为1，角频率为314 Hz，初相角为0°。输入双级矩阵变换器a相的相电压和相电流如图3所示，可知输入电压和电流几乎同相，即达到了最大的单位功率因数；整流级的输出直流电压如图4，可见整流级输出的直流电压中出现了零电压的情形；双级矩阵变换器输出的三相负载电流和线电压如图5、图6所示，可知双级矩阵变换器输出的三相电压和电流对称分布，且呈正弦规律变化。

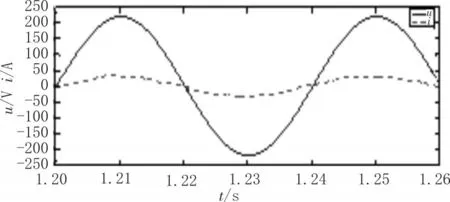
图3 矩阵变换器输入的a相电压和电流波形

图4 整流级的输出直流电压波形

图5 矩阵变换器输出的三相负载电流波形

图6 双级矩阵变换器输出的线电压波形

4 结 论

文中提出了在双级矩阵变换器整流级插入了零矢量的空间矢量调制策略，不需要修正逆变级的调制系数，输出直流电压局部平均电压恒定，电压利用率高。仿真结果表明双级矩阵变换器具有良好的输入输出特性，且换流简单可靠。

[1]Wei L，Lipo T A.A novel matrix converter topology with simple commutation[J].Proceedings IEEE IAS2001，2001（3）:1749-1754.

[2]孙凯，周大宇，梅杨.矩阵式变换器技术及其应用[M].北京:机械工业出版社，2007.

[3]宋卫章，钟彦儒，李洁.带相位补偿环节的双级矩阵变换器网侧电流闭环控制[J].电工技术学报，2010，25（7）:77-83.

[4]Rodriguez J，Kolar J，Espinoza J，et al．Predictive Current Control with Reactive Power Minimization in an Indirect Matrix Converter[C]//IEEE InternationalConference on Industrial Technology，2010:1839-1844.

[5]邓文浪，杨欣荣，朱建林.18开关双级矩阵变换器的空间矢量调制策略及其仿真研究[J].中国电机工程学报，2005，25（15）:84-90.

[6]陆晓楠，孙凯，李刚，等.双级矩阵变换器网策功率因数的控制方法[J].电工技术学报，2010，25（10）:108-114.

[7]李玉玲.电流型PWM整流器及其控制策略的研究[D].杭州：浙江大学，2006.

[8]杨勇，赵方平，阮毅，等.三相并网逆变器模型电流预测控制技术[J].电工技术学报，2011，26（6）:153-159.

[9]齐庭庭.双级矩阵变换器的预测控制策略研究[D].湖南：湘潭大学，2013.

[10]翟玉千.双级矩阵变换器的异步电机直接转矩控制系统研究[D].兰州：兰州交通大学，2012.

[11]党存禄，赵鹏林.双级矩阵变换器空间矢量调制策略改进[J].工矿自动化，2013（6）：56-61.

[12]董峰斌.整流级有零矢量的TSMC调制策略[J].电力自动化设备，2011（3）：66-70.

[13]赵卓鹏，贾石峰.直驱式风力发电系统矩阵变换器的控制研究[J].电气制造，2011（5）：42-44.

[14]张丽琼，潘峰.矩阵变换器空间矢量脉宽调制控制算法及仿真研究[J].电子世界，2012.

[15]戴钱坤.矩阵变换器的过调制技术研究与实现[D].南京：南京航空航天大学，2010.

[16]苏光靖.矩阵变换器控制策略的仿真研究[D].合肥：合肥工业大学，2009.

The analytical transformation and simulation of two⁃stage matrix converter

WANG Dan1，ZHAI Yu⁃qian2
（1.Faculty of Electrical Engineering，Xi’an Railway Vocationgalamp;Technical Institute，Xi’an710014，China；2.China North Car Tangshan Railway Vehicle CO.，LTD.，Tangshan064000，China）

In order to optimize the output performance of the two⁃stage matrix converter，and improve the voltage utilization ratio of that.This article proposed the space vector modulation strategy that zero vector modulation strategy is used in the level of the rectifier，based on the Analysis of two⁃stage matrix converter topology；On the ideology of the new modulation strategy，the rectifier level and inverter level are analyzed and converted，and their switch functions are calculated.Based on simulation，the local average voltage of the output DC voltage is constant，and the voltage utilization rate is 86.6%and the result shows that the modulation strategy is correct and feasible.

two⁃stage matrix converter；the rectifier level zero vector；switch functions；simulation

TN43

A

1674-6236（2017）22-0170-04

2016-10-20稿件编号：201610107

王丹（1984—），女，陕西华阴人，硕士研究生，讲师。研究方向：电力电子技术。