改进凸包插值算法结合大概率优化的演化算法

崔东，于湛麟

（渤海大学辽宁锦州121000）

改进凸包插值算法结合大概率优化的演化算法

崔东，于湛麟

（渤海大学辽宁锦州121000）

近似算法在解决超大规模旅行商问题时无法获得高精度优化解（或者次优解），智能算法虽然可以获得精度高于近似算法的解，很难在合理时间内获得。采用改良的凸包近似算法构成初始解并结合大概率优化策略的遗传算法来解决超大规模旅行商问题，通过对rl11849（962313），brd14051（489721），和pla33810（70757880）等实例实验都在理想的时间内获得优化解。证明这种混合算法在解决超大规模TSP问题时具有优势。

智能算法；近似算法；超大旅行商问题；混合算法

TSP问题（即旅行商问题）是典型的组合优化问题[1]。问题描述为：一名商人要到几个城市推销货物，从任意城市出发经过各城市一次且仅一次，然后回到出发点。由于该问题的描述简单[2]，而其实际规模在路径，网络，分配，调度和集成电路设计等优化问题中又有着广泛的应用[3]。其中精确算法在求解过程中，时间复杂度约等于O(n22n)。因为本文针对解决的是超大规模TSP问题，所以此类方法不做考虑。退而求其次，一些学者在近几年分别根据数学优化和人工智能（Artificial Intelligence）理论提出了两种TSP求解方法，即：近似算法[4]和智能算法[5]。

近似算法在求解TSP方面，以凸包算法为代表[6]，时间复杂度一般小于或者等于O（n4）。并且在小规模TSP实例中，该算法一般都具有良好的性价比。但是，在求解超大规模TSP方面，这些近似算法的精度有明显的下降趋势。并且，这些近似算法一般只能给出一个近似解。在智能算法求解TSP方面，有进化算法[7-9]和混合算法[10]。这些智能算法一般都具有全局搜索、并行处理和强鲁棒性等优点[11]。并且，在中等规模TSP实例测试中，这些智能算法的精度一般要高于上面提到的近似算法。但是，随着实例规模的增加，特别是对超大规模TSP来说，在算法后期寻优速度以及收敛速度都有明显的下降[12-13]，从而影响了TSP寻优的质量。这可能是由于在算法后期，随着优化解密度的急剧下降，隐含的寻优策略开始逐渐失效，从而产生大量的无价值的迭代运算影响算法的效率。

文中通过采用改进的凸包算法结合大概率优化策略的遗传算法，首先通过使用改进的凸包算法产生的一个不坏的初始解，解决智能算法对初始解较敏感的问题，可以为后面的迭代节省的大量的时间，然后采用基于大概率思想的遗传算法，对这个初始解进行深度优化，以期在理想的时间内找到一个较好的解。

1 改进的凸包算法

1.1 基本原理

点集H的凸包是指存在一个最小的凸多边形，其中点集H的点或是在这个凸多边形上或是在这个凸多边形的内部[14]。在解决TSP问题时由于问题需要将内部点插入到凸包上形成回路初始解的方法有很多，由于演化算法对初始解比较敏感的特性，如果能对初始解的精度提高一些，可以为后面的演化算法节省大量的时间，本文针对提高算法精度的问题找到了更好的解决方法。

首先找到该点集的第一层凸包，使用凸包算法找到这些点后，将第一层凸包点顺序保存并从点集中将第一层凸包点删除。然后继续使用快速凸包寻找第二层凸包点集，算法结束后将第二层凸包点顺序保存并从点集中将第二层凸包点删除。如此操作直到点的个数小于4算法停止。由于旅行商问题的特性需要将这些层凸包形成回路，将最外层凸包的下一层凸包的点按照最小增量的方法依次插入到最外层凸包当中，直到所有点形成回路算法结束。

1.2 算法框架

算法1：构成回路的算法

输入：点集H

输出：各层凸包T0，T1…Ti-1，Ti

While（H＜4）//i=0。点集H为当前城市点的集合，当点集H中的点个数小于4时算法停止

{Ti=Convex（H）；//Tubao（）是求取当前点集H的凸包Ti的算法

H=H-Ti；//将已经找到的该层凸包Ti按顺序保存并从点集H中删除

i++；}

输入：各层凸包T0，T1…Ti-1，Ti

输出：哈密尔顿回路T0

while（j＞i）//j=1；

{将Tj层凸包的所有点按照最小增量的方法插入到T0层凸包当中，将两层凸包形成一条新的回路；j++；}

算法2：Convex（）//改进的凸包的快速算法

步骤1：Initial（H）//初始点选择函数。

首先找到一个或多个y值最小的点。如果有多个这样的点，再比较其x值，将这些点中x值最小的点作为该层凸包的初始点。

步骤 2：Center（H，O[2]）//点集的中心点求取函数。

设点集H共有n个点，a为n个点x值的总和，b为n个点y值的总和。O[0]=a/n，O[1]=b/n。

设点O的x值为O[0]，y值为O[1]，点O为该点集的中心点。

步骤 3：Authentication（）//寻找初始点下一个该层凸包点的函数。

点p为初始点，点O为中心点，设点q为待验证该层凸包的下一个点，设点集K为除初始点和待验证点以外所有点的集合。

while（j＜n-1）

{while（i＜n-2）//n当前点集的总个数，i=0

{A=Intersection（p，q，Ki，O）//A点为初始点和待验证点与中心点和Ki点的交点

if（distance{O，A}+diatance{A，Ki}==distance{O，Ki}）{break；}//若存在 Ki点在 p 点和 q 点连线的外部，则该q点不是这层凸包的下一个点。

else{i++；}}//若该q点通过点Mi的测试则继续测试点Mi+1，直到测试所有n-2个点停止。

if（i!=n-3）{q=q-＞next；}//若该q点没有通过点集K中所有点的验证则寻找下一个待验证点q。

else{break；}}//若该q点通过所有K点集中所有点的验证，则该q点为该层凸包的下一个点。将q点作为该层凸包的下一个初始点p重复执行步骤3，直到找到的q点为第一个初始点算法结束。

2 大概率思想的演化算法

2.1 基本思想

在解决旅行商问题时，精度与时间往往是评价算法优劣的重要标准。而在利用演化算法解决超大旅行商问题时，对局部优化的时间和精度往往不好掌握，结果会导致大量的冗余结算占用大量的时间最终导致无法在规定时间内获得较好的解。本文针对这个问题采用大概率思想的演化算法，首先通过对已经给出优化解的小型TSP实例进行统计以期选择最佳的优化局部半径，对其优化可以最大概率的得到较好的优化解，其次优先对局部范围内找到优化解的周围寻找更好的结果，直到优化解不在满足设定的阈值停止算法并找新的局部范围进行优化。这样即提高了局部的优化效果，又能对下次可以获得较好优化效果的标准点做出选择，可以使每次的优化都是大概率事件。

证明:设实例V={v1,v2…vn}，平均距离。如果存在A⊂V，B⊂C，A⋃B=V，并且，那么称r为近邻系数。

假设存在一个函数f(r)，并且误差，即：函数f(r)→。那么，称f(r)为近邻系数r的概率密度函数，为近邻系数r的概率分布函数。

文中通过对上述TSP实例库1002个点以内部分已经给出优化解的实例进行统计，具体统计方式为:

首先计算出已经给出优化解的实例n中点a1与其下一个a2的路径长度，然后计算点a1与其余n-2个点的路径长度，将a1到a2的路径与这些路径进行排序，对该实例中所有点都统计后设ai到aj路径与ai到其余n-2个点排序最大为k。通过统计发现，随着实例点的增加k值也会有相对的增加，其中pr1002实例的k值达到24，也就是说只有随着实例点的增加扩大优化局域半径才能够确保其可能搜索到该实例中最好的优化结果。

通过这种统计方式来对局部进行优化的优势是明显的：可以保证标准点的最可能获得优化解下一个点在这个局域内，这样优化的时候也就可能获得该局部内最好的解，从整体来看，若一个区域得到优化对其周边区域进行优化同样也是大概率事件。然而这个优化大概率事件随着深度的增加所产生的问题也是明显的:随着其运算次数的增加，其精度难以保障而出现下溢。针对上述问题本文给出的解决方法是：根据不同的实例设定相应的阈值，当优化速度达到阈值的时候停止，寻找新的范围进行优化。

2.2 算法框架

输入：初始种群T

输出：优化后的种群T0（若没有得到优化保留初始种群T）

while（i＜n）//i=0；n为迭代次数

{T1=Code（T，a，n）；//T 为初始解，以a点为中心，对距离其最近的n个点进行编码

//1万点的实例到2万点的实例k值取30，3万点的实例到4万点的实例k值取40，4万点以上的实例k值取50

T2=optimization（T1）；

if（f（T1）＜f（T2））//f（）为适应度函数

{T0=Decode（T2）；

While（j＜m）{T3=Code（T，am，n）//am 是指以a点为中心距离最近的第m个点

T4=Optimization（T3）；if（f（T3）-f（T4）＞M）{T0=Decode（T4）；}//M为阈值；若T3局部解得到优化则对T4进行解码将结果对种群T0覆盖

else{break；}//若优化值小于阈值停止该层优化

j++；}}else{若T1没有得到优化重新选择标准点进行优化}i++；}

2.3 编码/解码函数

文中采用的是局部优化策略，求解TSP问题的编码/解码方法有很多，本文采用的路径表示法。

编码（Code（））

输入：T初始种群；标准点a；距离a最近的k个点

输出：优化后种群T1

以a点为标准点，从初始种群T中选出距离其最近的k个点，按照T中的顺序排列生成其子代T1，并对其余的没有参与编码的路径进行保存。

解码（Decode（））

输入：参与优化后的子代T1，编码中保留的有向路径

输出:参与优化后的种群T0

将编码操作中保留的有向路径按照最小增量方式插入到子代T1中形成新的种群T0

2.4 适应度函数

适应度函数用来评价新生个体的优劣程度，文中采用的适应度函数为路径行径长度的倒数来表示个体的优劣程度。根据适应度的大小来对子代个体选择是否保留，保证使更符合标准的子代个体有更多的存活机会。

2.5 优化函数

超大旅行商问题与小规模旅行商问题相比城市点较多，分布较密集，导致其在优化的初期较容易而且优化速度较快，只需要调整较少的边数就可以获得更优解，本文在算法初期和中期优化的方法是:通过调整4个城市点的排列方式来获得更优解，随着算法运行时间的增加需要对局部解进行增加优化的次数。调整方法如下:

优化函数（Optimization（））

输入：初始种群T，局部解T1

输出：若局部解得到优化则输出优化解T0，否则保留初始种群T

T1=Code（T，a，k） //T1为T的局部解

While（N＜4）{cityN=Random（T1）；N++}//从局部解T1中随机选择4个城市点位 b0，b1，b2，b3

对这4个城市点排列组合共有23种排列方式（除初始状态以外）最少需要调整两个城市点的位置，最多需要3个城市点位置。若调整两个城市点位或者3个城市点位后T1得到优化，则保留当前调整后的结果，否则将其还原成调整前的状态。

T2=exchange（city1，city2）//交换两个城市点的位

if（f（T1）＜f（T2））{T0=Decode（T2）；}//若T1得到优化，对T2局部解进行解码得优化种群T0

else{exchange（city1，city2）}//若 T1 没有得到优化，将两个城市点还原

3 实 验

为检验文中的算法性能，通过3次实验求解标准问题库TSPLIB中一万点以上的部分实例（实验环境：CPU为因特尔3.10GHz，内存为4.00GB，操作系统为win7，编程语言为c语言，编程工具为Microsoft Visual C++。）实验结果如下方表图所示。从实验结果来看，其中pla33810（70757880.60），brd14051（489721.70）和实例 rl11849（962313.90）所获得的 3次实验结果均好于文献[2]的实验结果。

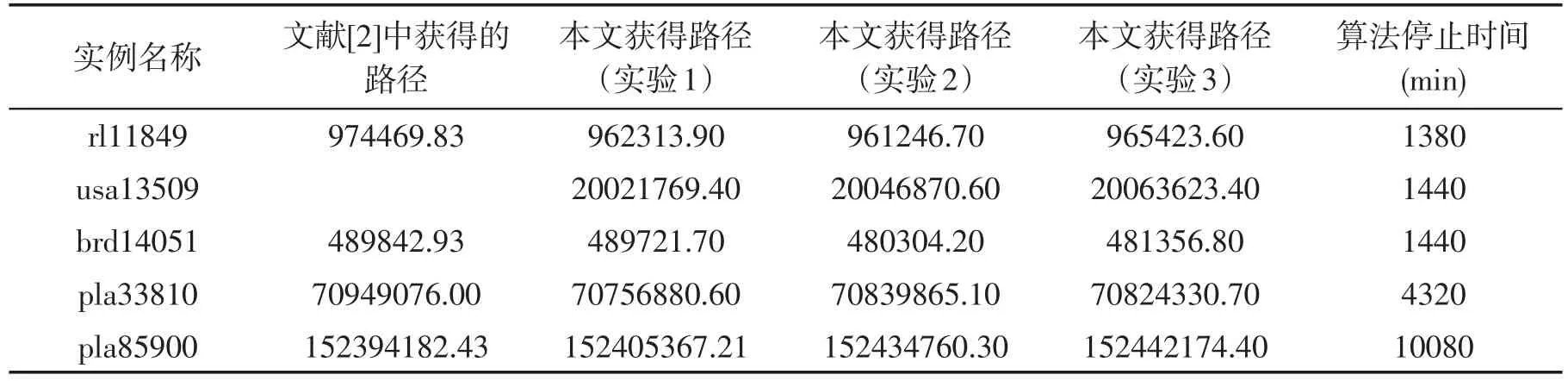
表1 TSPLIB中超大规模实例的实验结果

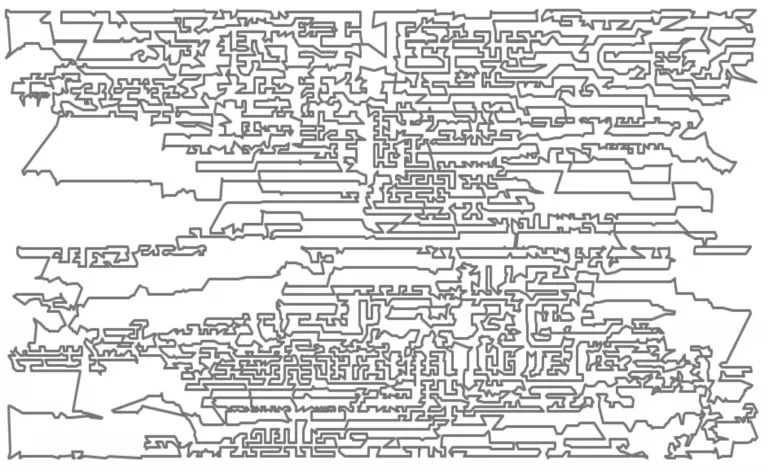
图1 rl11849的实验1优化路径（962313.9）

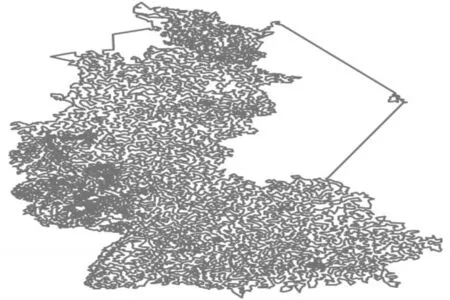
图2 brd14051的实验1优化路径（489721.7）

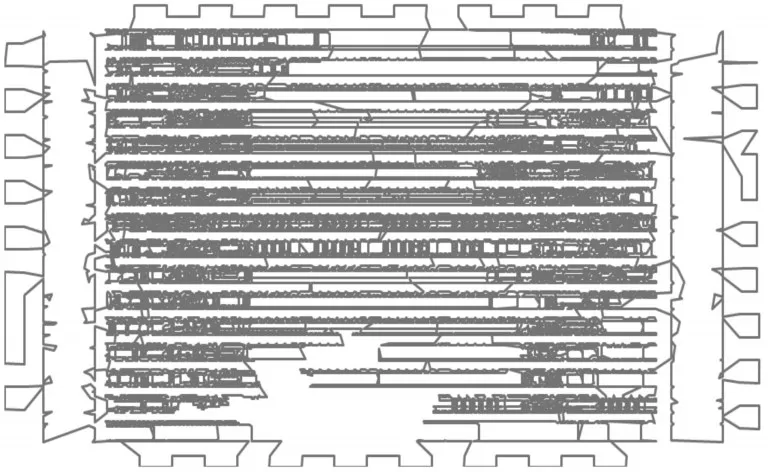
图3 pla33810的实验1优化路径（70757880.6）

4 结束语

演化算法发展至今已经经历了40多年，无数的学者投身其中。随着计算机技术的发展，演化算法又步入了新的阶段。目前针对旅行商问题这一演化算法试金石的解决，只有当问题规模较小时，可以在合理的时间内获得高精度的解，在解决超大规模旅行商问题时，还是有许多不足，无论是近似算法或者智能算法都遇到了不同的困难。虽然本文可以对一些超大旅行商实例在合理的时间内给出较好的解，但是这也是针对文献[2]的结果相比较而言的。之所以可以获得较好的结果是因为在初始值的产生方法和选择标准点优化策略的方法上较前人而言较新颖，可以很大概率上寻得较好的解，提高了算法的效率。在未来针对解决超大旅行商问题的混合算法将是研究的热点和重点。

[1]许文超.混杂运行条件下客运专线动车组运用优化研究[D].北京：北京交通大学，2013.

[2]赵连朋，金喜子，王娜，等.求解超大规模旅行商问题的纵深遗传算法[J].计算机工程与应用，2009，45（4）：56-58.

[3]Osaba E，Carballedo R，Diaz F，et al.On the influence ofusing initialization functions on genetic algorithms solving combinatorial optimization problems:A first study on the TSP[C]//2014 IEEE Conference on Evolving and Adaptive Intelligent Systems（EAIS），2014.

[4]赵海森，杨承磊，吕琳.多边形中的点可见性快速算法[J].计算机辅助设计与图形学报，2013，25（3）：331-340.

[5]张贵军，何洋军，郭海峰，等.基于广义凸下界估计的多模态差分进化算法[J].软件学报，2013，24（6）：1177-1195.

[6]杨玉婷，康厚良.2D图形引擎中的平面多边形内外点判别[J].图学学报，2013，34（3）：100-102，105.

[7]张宇翔，黄力宇.Hopfield网络求解TSP两种改进算法的仿真研究[J].电子设计工程，2009（10）：119.

[8]程毕云，鲁海燕，徐向平，等.求解旅行商问题的改进局部搜索混沌离散粒子群优化算法[J].计算机应用，2016（1）：138-142.

[9]王宝生，屈宝存.蚁群算法在求解TSP问题中的改进研究[J].电子设计工程，2014（22）：14-18.

[10]姚明海，王娜，赵连朋.改进的模拟退火和遗传算法求解TSP问题[J].计算机工程与应用，2013，48（14）：60-65.

[11]Yu Yingying，CHEN Yan，LI Taoying.A New Design of Ge-netic Algorithm for Solving TSP[C]//2011FourthInternational Joint Conference on Computational Sciences and Optimization，2011.

[12]李煜，马良.用量子蚁群算法求解大规模TSP问题 [J].上海理工大学学报，2012，34（3）：355-358.

[13]盛虹平，马良.求解大规模旅行商问题的改进大洪水算法[J].小型微型计算机系统，2012，33（2）：259-262.

[14]范美玲.面向场景的TD-LTE无线参数优化配置系统设计与实现[D].北京：北京邮电大学，2014.

Improved convex hull algorithm combined with probability optimization evolutionary algorithm

CUI Dong，YU Zhan⁃lin
（Bohai University，Jinzhou121000，China）

The approximate algorithm can not obtain the high accuracy optimization solution（or sub optimal solution）when solving the problem of super large scale traveling salesman problem.Although the intelligent algorithm can obtain the solution of the algorithm with higher accuracy than the approximate algorithm，it is difficult to obtain the.By using the improved convex hull approximation algorithm and genetic algorithm are combined to constitute the initial solution of the probability optimization strategy to solve large scale traveling salesman problem，based on the rl11849（962313），brd14051（489721），and pla33810（70757880）and other examples of experiments in the ideal time to obtain optimal solution.It is proved that the hybrid algorithm has the advantage of solving the problem of super large scale TSP.

intelligent algorithm；approximation algorithm；large traveling salesman problem；hybrid algorithm

TN609

A

1674-6236（2017）22-0026-05

2016-09-24稿件编号：201609220

崔东（1992—），男，辽宁沈阳人，硕士研究生。研究方向:规划识别。