改进的弹性补偿有限元法在河堤极限承载力计算中的应用研究

2017-12-01贾秀娟

水利规划与设计 2017年10期

关键词：抗拔有限元法堤防

贾秀娟

（铁岭市水利工程规划设计技术审核中心，辽宁铁岭 112608）

改进的弹性补偿有限元法在河堤极限承载力计算中的应用研究

贾秀娟

（铁岭市水利工程规划设计技术审核中心，辽宁铁岭 112608）

文章引入改进的弹性补偿有限元法对辽宁北部某河道堤防的极限承载力进行了计算，并结合原位螺旋桩抗拔试验对比分析不同方法的极限承载力计算精度。结果表明：改进的弹性补偿有限元法结合弹性模量对承载比阈值进行调整和改进，相比于传统方法，其计算误差减少13.9%，且迭代计算收敛效率也明显高于传统方法，改进效果明显。通过工程实例的极限承载力分析，表明河道堤防较易在其中心轴线出现失稳情况。改进的弹性补偿有限元法可在实际工程设计中进行推广和应用。

改进的弹性补偿有限元法；弹性模量；承载比；原位螺旋桩抗拔试验；河堤极限承载力

河道堤防工程设计需要对堤防的极限承载能力进行计算，极限承载力是衡量河道堤防安全的重要指标。目前针对极限承载力计算的方法主要有经验分析法［1］、模型试验法［2］以及数值分析计算法。在各种数值分析方法中，基于有限单元的弹性补偿方法在极限承载力计算中应用较为广泛［3-6］。但是传统弹性补偿方法在失稳判定时存在较多的人为主观性，受主观要素影响较大，因此极限承载力计算误差相对较大。近些年来，可综合考虑弹性模量的改进弹性补偿有限元法在许多领域极限承载力的计算中得到应用［7-9］，但在河道堤防的极限承载能力计算中还未得到具体应用。为此本文引入改进的弹性补偿有限元法对辽宁北部某河道堤防的极限承载力进行了计算，并结合原位测试数据对比分析了改进前后的弹性补偿方法在极限承载力计算的精度。

1 改进的弹性补偿有限元法的河道堤防极限承载力计算原理

传统的弹性补偿有限元法以承载比来表征计算单元的内外屈服程度，其计算方程为：

式中，ηe，i-河道堤防极限承载比；Se，i-不同计算有限单元的等时效堤防承载应力；Se，0-不同计算有限单元承载比屈服度，其中Se，i的计算表达式为：

式中，σij-计算有限单元的应力分量；σs-有限单位的材料强度系数。

在进行承载比的基础上传统的弹性补偿方法以承载比均匀程度对河道堤防的极限承载结果进行定义，承载均匀度计算方程为：

式中，d-河道堤防极限承载均匀度；-ηi-各有限元承载比的均值； ηmax，i和 ηmin，i-计算有限单元最大和最小承载比值，其计算方程为：

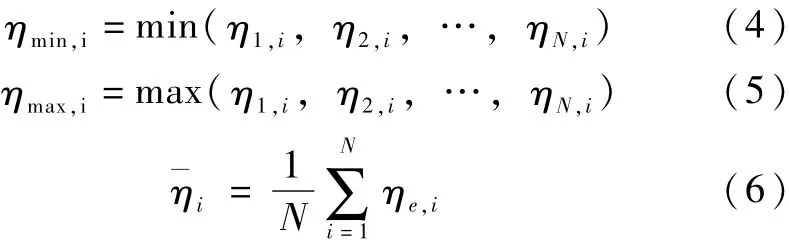
在方程（4）、（5）、（6）中 N表示计算的有限单元的总数。传统弹性补偿有限法采用弹性模量来对承载比的阈值进行调整和改进，改进方程为：

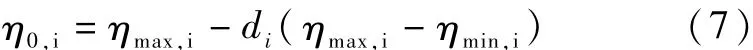
在方程（7）中 η0，i表示为河道堤防稳定结构的承载比基准值。

结合能量守恒定量，进行调整后的河道堤防弹性模型与调整前的有限单元变量耗能总和为：

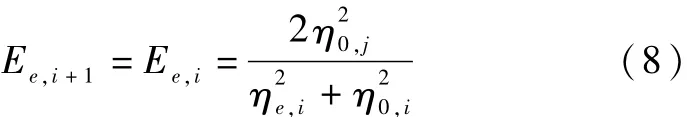
改进的弹性补偿有限元法对不同有限单元的弹性模型进行改进，改进后的能量方程为：

此外改进的弹性补偿方法在进行有限元分析时，第i次迭代计算时最大承载比和堤防外力负荷呈现线性变化关系，则计算的第i次极限荷载的计算方程为：

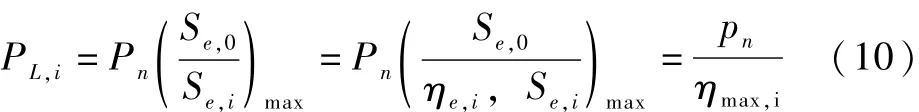
其中在方程（10）PL，i表示为第 i次迭代计算得到的河道堤防极限承载；Pn表示为基准荷载值。

2 实例应用

2.1 河道堤防概况

本文以辽宁北部某河道堤防为工程实例，该河道堤防的主要岩性特征参数见表1。该河道堤线长3.0km。现状堤顶高程11.4～12.8m，堤顶宽5.5～12.5m，有宽3m左右泥结碎石路面；迎水坡比大部分地段约1∶3，局部较陡处约1∶2.5。本文基于河道地形数据，采用有限体积单元格式对河道堤防进行空间离散（见图1），河道堤防共离散112856个有限单元。

图1 河道堤防离散单元

表1 河道堤防各岩体材料特性参数

2.2 原位螺旋桩抗拔试验及堤防极限承载力计算结果对比

采用螺旋桩抗拔试验对不同桩号堤防极限承载力进行了原位测试，并结合改进前后的弹性补偿方法结合表2中各桩段的特性参数，计算了不同桩段堤防的极限承载力，计算结果见表3。

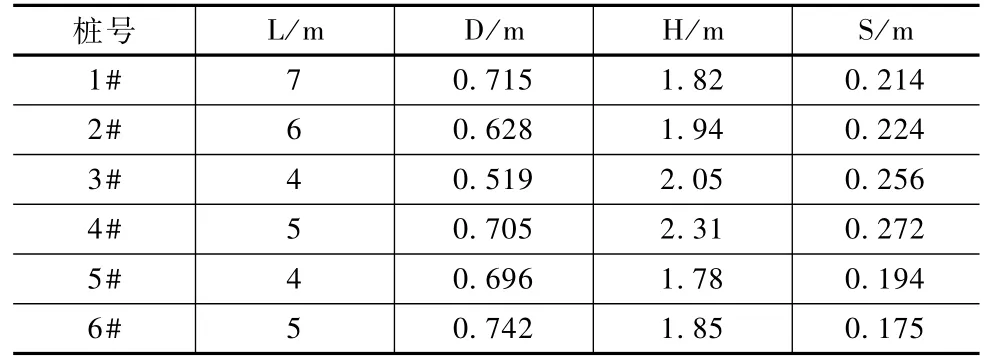
表2 螺旋桩抗拔试验各桩号特性参数

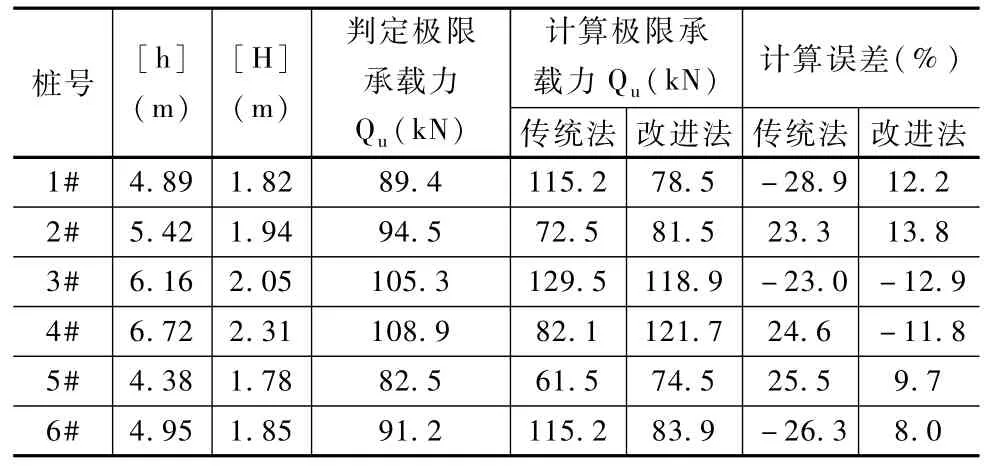
表3 螺旋桩抗拔试验各桩号极限承载力

本次对6个桩段进行了7组抗拔试验，结合沈保汉［10］进行的螺旋桩抗拔试验研究成果，当螺旋桩抗拔试验的桩头顶部荷载及其荷载位移变化曲线突然上升点位移达到20mm时，则可以判定其堤防荷载为极限荷载，从表3中可以看出，当1#桩段其打桩深度达到4.89m时，其判定的极限承载力为89.4kN，2#桩段打桩深度为5.42m时，其桩段出现失稳现象，判定该桩段出现极限承载现象，2#桩段极限承载力为94.5kN，3#和4#桩段在螺旋桩的打桩深度达到6.16m和6.72m时，其桩段出现极限承载现象，其极限承载力分别为为105.3kN和108.9kN。第5#和第6#桩段在进行抗拔试验时，当抗拔深度为4.38m和4.95m时，其桩段达到极限承载，极限承载分别达到82.5kN和91.2kN。从计算误差可以看出，改进的弹性补偿方法计算的极限承载力和原位螺旋抗拔试验判定的各桩段极限承载力之间的误差在8.0%～13.8%之间，而传统的弹性补偿方法计算误差在-23.0%～-28.9%之间，相比于传统方法，改进方法在极限承载计算误差上减少13.9%。产生计算误差的主要原因在于假定的堤防基准面和实际的堤防基准面有所差距。

2.3 河道堤防极限承载比计算对比试验

河道堤防极限承载比是河道堤防稳定性评价的重要参数，为此本文采用对比试验的方式分析不同计算方法对河道堤防极限承载比的影响，分析结果见图2。

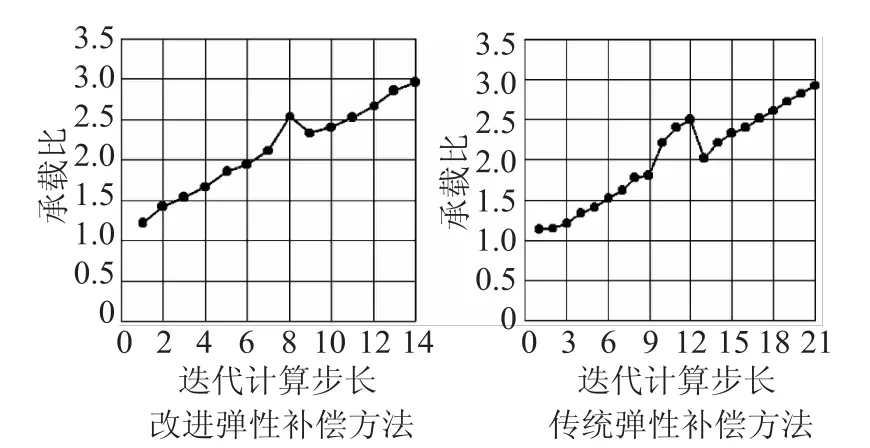
图2 不同方法河道堤防极限承载比计算对比结果

从图2中可看出，改进的弹性补偿有限元法随着迭代步长的增加，其河道堤防极限承载比也逐步增加，当迭代步长达到14时，不同计算单元承载比的差小于收敛最小方差，计算迭代终止。而传统的弹性补偿方法下其迭代计算步长达到21时，其计算单元的承载比小于收敛最小方法，迭代计算终止。从对比试验结果可以看出，改进的弹性补偿有限元法计算收敛速度要快于传统的弹性补偿方法，改进的弹性补偿有限元法计算效率要明显高于传统方法。

2.4 基于改进弹性补偿有限法的河道堤防极限承载能力分析

在对比试验分析的基础上，结合改进的弹性补偿有限元法对河道堤防的极限承载力的纵向分布进行了计算分析，计算结果见图3。

图3 河道堤防上下两弦段极限承载应力纵向分布图

从图3中可以看出，在河道堤防的上弦截面，其最大值应力变化过程的最大点主要出现在800m处，该段堤防的的材料主要为IVa类岩体，其极限承载力最大，而同样在2400m和2600m处也同样出现极限承载最大值。而从1100～2300m河道堤防上弦截面的极限承载呈现下降变化，这部分主要由于刚度较低原因使得其极限承载力下降较为明显。从堤防上弦截面应力最小值极限承载最大值分别出现在1000、2400、2800m处，经过分析该三处截面堤防主要的材料为Ⅲb类岩体，属于承载比较大的岩体，而其他部分出现极限承载下降的原因也同样是因为刚度较低。从图中堤防下弦截面应力最大最小纵向变化过程可以看出，其下弦截面应力最大值的极大点分别出现在1000、2000、2800m处，出现极大点的原因主要这三段堤防的岩体材料的极限承载比较大。当下弦刚度降低时，其下弦截面应力最大值也逐步出现极小承载点。从堤防下弦截面应力最小值的纵向分布中可以看出，在 600、1000、3000m出现最小应力的极大点。综上可以看出，改进的弹性补偿方法可有效的对河道堤防纵向的极大承载力分布进行分析，随着极限荷载的增加，其极限荷载沿着河道堤防纵向沿轴线不断加大，应注重河道堤防轴线出现极限承载的失稳性。