不同潮汐预报模式在近海海域的准确度评估

刘 潘，李树军，艾丛芳

（1.大连理工大学水利工程学院，辽宁 大连 116024；2.中交天津港湾工程设计院有限公司，天津 300400）

不同潮汐预报模式在近海海域的准确度评估

刘 潘1，李树军2，艾丛芳1

（1.大连理工大学水利工程学院，辽宁 大连 116024；2.中交天津港湾工程设计院有限公司，天津 300400）

潮流是海岸河口主要水动力因素之一。为了解海岸河口潮流场特性，一般采用物理模型实验模拟和数值模拟的方法，这两种方法都涉及到开边界的问题。文章介绍两种用于预测潮汐变化从而获得开边界条件的模式，即大洋潮汐同化模式（TPXO）与调和分析模式，并对其在近海海域预测的准确性进行对比分析。结果表明：两种模式均能较好的拟合实测数据，调和分析模式在近海海域的精度更高，更适合计算河口潮流场模拟的开边界条件。

开边界；近海潮汐预报；TPXO；调和分析

随着科技的发展，卫星高度计在潮汐学中的应用越来越广泛，TOPEX/Poseidon卫星（以下简称T/P卫星）以及其后继的Jasan1/2卫星的发射升空，为潮汐分析积累了大量高精度、高分辨率的测高数据［1-3］，在此基础上全球大洋潮汐模式已发展了数十种。迄今人们已经建立了多种全球大洋潮汐模式，根据其方法的不同，可以把它们大致分为三类［4-5］：第一类是大洋潮汐的经验模式。这类模式主要基于地面或卫星测高资料，利用主观或客观分析等；第二类是潮波动力学模式。这类模式利用潮波方程进行数值模拟得到全球大洋潮汐分布经验的方法获得大洋潮汐分布；第三类是大洋潮汐同化模式。这类模式是基于潮波动力方程，采用各种同化方法，利用潮汐实测资料来提高潮汐模拟结果的准确度，从而获得全球大洋潮汐更准确的分布。数据同化技术将潮位观测资料与动力模式有机结合，从而反演出潮流信息，对于中、小尺度问题，数据同化方法优势非常明显［6］。

调和分析作为传统的潮汐预报方法是以潮汐静力学和动力学为基础，经过多年发展，已经能够实现对潮汐进行稳定、长期预报，需要利用大量长期的潮位观测数据得出准确的调和分析模型。

1 大洋潮汐同化模式（TPXO）预报潮位的原理

本文选用属于第三类大洋潮汐模式的由美国俄勒冈大学开发的大洋潮汐同化模式（TPXO），TPXO［7-8］使用一种 Generalized Inverse Method 从潮位观测数据中提取潮流信息。这种方法基于将38周的T/P数据获得的交叉点分析结果同化于潮波动力学方程而获得的全球反演解。模型的分辨率为0.6°×0.7°（纬差 ×经差）， 模型域跨越 80°S到 70°N的纬度范围。

1.1 TPXO模型对T/P数据的交叉点分析

该模型计算的分潮数 L=8（K2， S2， M2， N2，K1， P1， O1， Q1）， 分潮的频率记为 ωl，l=1，L。该模型用复振幅以及流量的纬向和经向分量ul和vl，再加上海拔高度 hl描述某个分潮的状态，这些量都是位置x的复值函数。通过复杂的3L维向量场给出潮汐状态的完整描述［8］：

从中可以计算可观测的潮汐量。例如，由潮汐仪观测的海平面作为通用时间和位置的函数由下式表示：

式中，Vl（t0）-组分l在 t0时刻的天文参数。如果掌握足够长时间序列的潮位计测量数据，经过调和分析，可以直接分离计算出某个分潮的海拔高度；但是对于只掌握短期观测数据，尤其是卫星测高数据，调和分析是不可行的。因此需要对（2）式进行假设和简化［9］，不考虑次要分潮：

式中，αl（t）-具有长周期（18.6年）的振幅和相位调制［10］， 用来代替（2）式中的指数函数［8］。

在对h（x，t）进行修正，必须考虑另外两个影响因素：

一是源于地球的弹性屈服而产生的地心潮h′（x，t） ， h 和 h′的关系近似为下式［11］：

为了更加准确估计潮汐状态u并得到校正的高度数据h′（x，t），这里采用一种通用的简单标量校正因子，校正的高度数据可以表示为：

二是为了消除大地水准面（其非常大）中的不准确性影响，需要考虑消除在相同位置不同时间的高度数据之间形成的差异。具体采用的方法是交点差异法，卫星在10天的轨道周期中升轨和降轨的过程中存在I个轨迹交点，随机选取xi（1≤i≤I）处卫星升轨和降轨时对应时间和得出的校正高度数据，以此计算交叉差异：

“当时野生菌在深圳的市值差不多是40元每公斤，而酒店里一盘炒鸡枞卖到120元，一盘菜也就只需要一公两的原料而已，相当于一公斤鸡枞就可以卖到八九百元。”李志勇和酒店顺利达成了合作协议，他也明白，要让家乡的产品走出去，我们首先要自我“包装”，更要将家乡丰富的纯天然产品也好好包装一下。他风风火火赶回家，跟妻子一起精心挑选了20几个品种的野生菌发往深圳，不到半年，生意逐渐有了方向。

该方法同时对潮汐测高数据的调和分析和T/P卫星数据的交叉差异两种情况进行考虑。在这两种情况下，数据可以被视为作用于状态空间中元素的具有附加测量误差的线性函数输出，将全部数据集设为长度为K的向量d，其满足下式：

1.2 TPXO模型的潮波动力方程

为了使频率ωl处的潮汐场ul=（ulvlhl）T满足线性浅水方程，对自身吸引力和潮汐负荷的影响进行了校正［12］，在计算域O中满足下式：

该方程受∂O的边界条件约束。域O可以表示全海域或者部分海域。式中，-构成 l的天文强迫，用于校正固体地球潮汐，差分运算符Sl由下式给出：

式中，H=H（x）-海洋深度；f-科里奥利加速度；ωl-分潮的频率；▽和 ▽·-地球的二维梯度和发散算子；κ-耗散；G*-潮汐载荷和自身吸引力的格林函数的卷积，在（9）式中，对G*进行近似简化，取为常数β=0.9［13］。式（9）需要满足下面两个边界条件：

在求解过程中，水深H取自ETOPO5数据库，以10m水深作为限定勾勒出计算域O的边界，在北冰洋的北部边缘设置开边界条件（11）；深度采用Schwider的模型“SCH80”测得的数据。再将耗散κ进行简单的参数化：

在该返演方法中，动力学被用作弱约束，因此可以进行上述简化；基于同样的原因，在求解潮汐方程中忽略了水平粘度，并使用标量近似法简化潮汐负荷和自吸力。

综上所述，采用这种广义逆方法对卫星数据进行的返演，充分考虑测量误差和动态误差，在最小二乘的前提下，所得的数据最能满足拉普拉斯潮汐方程和T/P交叉点数据。与仅基于卫星资料提取的经验潮汐模式相比，同化模式具有可以在浅水区域用潮波动力模式进行补插的优点；与纯潮波动力学模式相比，同化模式可以用卫星资料和验潮站资料来提高准确度。

2 调和分析预报潮位的原理

调和分析预报潮位变化是用分潮调和常数预报潮汐［14］，将潮汐看成是以不同频率传播的各种潮波叠加产生的现象，调和分析的目的就是求出各个分潮的振幅和迟角，本文选取海域 K2，S2，M2，N2， K1， P1， O1， Q1， Sa等 9个主要分潮， 并利用沿海验潮站资料以及卫星高度计资料进行调和分析，进而获取分潮的调和常数，通过内插从而获得计算域范围内任意点处的调和常数，进而利用POM三维潮汐数值模式计算潮位变化［15-16］。

任意一个分潮的潮位表达式如下：

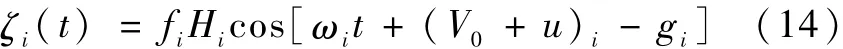
式中，i-分潮序列号；ζi-分潮潮高；ωi-分潮的角速度；fi-分潮i的交点因子，表示由于月球轨道18.61年的周期变化引进的对平均振幅H订正值，交点订正角；V0-格林威治初相角；（V0+u）i-i分潮的格林威治零时平衡潮分潮的初相角；Hi和gi-分潮i对应的平均振幅和迟角。潮汐理论指出：由月球和太阳的引潮力引起的潮汐是多个余弦函数的叠加［17］，因此潮位可表达为：

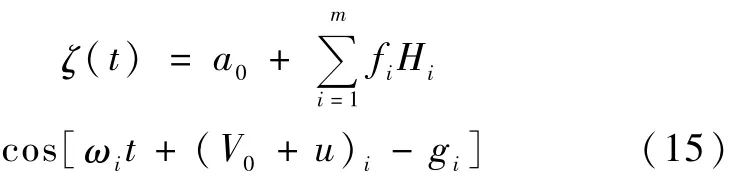
式中，a0-平均海平面；m-分潮数。这里没有考虑非天文潮位，视 a0-ω=0°/h的一个特殊分潮，潮高表达式可写为［18］：

只要通过潮汐分析得到各分潮的A、B值，即可得到分潮的振幅R和初相角θ，从而可求得调和常数。

3 两种模式误差对比及结果分析

TPXO模式预测潮汐在全球范围内的准确性已经得到充分验证［8］，这里主要考察该模式在渤海范围内潮汐预报的准确性。

为了对比两种潮汐预报模式在中国近海海域的差异，并对它们的精确度进行对比分析，我们利用中国海事服务网的潮汐预测数据作为实测数据，将计算得出的结果进行对比分析。中国海事服务网发布的潮汐表是依托国家海洋信息中心的专业数据支持，其准确度可以满足对比的要求。本文选择的潮位验证点为大连老虎滩验潮站（121°41′E， 38°52′N）， 验证时间为 2015-07-1300∶00～2015-07-1524∶00 以及成山角验潮站（122°41′E， 37°23′N）， 验证时间为 2015-07-3100∶00 ～2015-08-0224∶00， 各 72h整点潮位数据，两种模式预报结果与实测结果比较见图1～2（统一到平均海平面）。

为了更加直观的说明对比结果，这里采用一种考察潮高之差的均方根误差的方法，潮汐预报的均方根误差ERMS，其表达形式为：

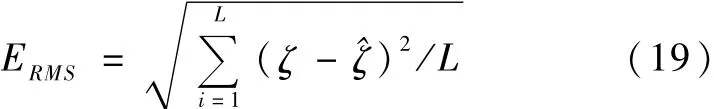
式中，L-潮汐样本数目；ζ-潮汐实测值；^ζ-潮汐预报值。对比结果见表1：

图1 两种模式预报与实测结果对比

图2 两种模式预报与实测结果对比（成山角验潮站）

表1 对比结果（单位：cm）

由图1～2和表1的对比结果，两种模式预测潮汐数据均能较好的与实测数据拟合，但调和分析模式比TPXO模式在近海海域具有更加精确的预报效果。

4 结语

为了提供潮流场模拟时开边界条件，本文分别简述了大洋潮汐同化模式（TPXO）和一种基于调和分析方法预测潮汐的原理，并针对中国近海海域对两种潮汐预报模式的准确性进行了对比分析。分析结果表明，采用广义逆方法的TPXO模式虽然在全球尺度的准确性已经被证实，但其在中国近海尤其是在水深较浅的渤海海域，准确度较低；而采用调和分析对潮位进行预测，在近海海域的准确度较高，能够满足模拟潮流场时对开边界条件精度的要求。

［1］ Munk W H.Once again： Once again-tidal friction［J］.Progress in Oceanography， 1997（40）： 7-35.

［2］ Tapley B D，Chambers D P，Shum C K.Accuracy assessment of the large-scale dynamic ocean topography from TOPEX/POSEIDON altimetry［J］.Journal of Geophysical Research， 1994， 99（C12）：24605-24619.

［3］何宜军，陈戈，郭佩芳，等.高度计海洋遥感研究与应用［M］.北京：科学出版社，2002.

［4］ Zahran K H，Jentzsch G，Seeber G.Accuracy assessment of ocean tide loading computations for precise geodetic observations［J］.Journal of Geodynamics， 2006（42）： 159-174.

［5］ Matsumoto K， Takanezawa T，Ooe M.Ocean tidemodels developed by assim ilating TOPEX/POSEIDON altimeter data into hydrodynamicalmodel： A globalmodel and a regional model around Japan［J］.Journal of Oceanography， 2000（56）： 567-581.

［6］ Shum C K，Woodworth P L，Andersen O B，et al.Accuracy assessments of recent global oceantide models［J］.Journal of Geophysical Research， 1997， 102（C11）： 25173-25194.

［7］ Egbert G D， Erofeeva S Y.Efficient Inverse Modeling of Barotropic Ocean Tides［J］.Journal of Atmospheric and Oceanic Technology，2002（19）： 183-204.

［8］Egbert G D，Bennett A，Foreman M.TOPEX/POSEIDON tides estimated using a global inverse model［ J］.Journal 0 f Geophysical Research， 1994（99）： 24821-24852.

［9］ Munk W H， Cartwright D E， Tidal spectroscopy and prediction［J］.Philos.Philosophical Transactions of the Royal Society，1966（259）： 533-581.

［10］ CartwrightD E，Tayler R J.New computations of the tide-generating potential［J］.Geophysical Journal International， 1971， 23（01）：45-73.

［11］ Ray R D，Sanchez B V.Radial deformation of the earth by oceanic tidal loading［R］.NASA Technical Reports Server， 1989： 10074.

［12］ Hendershott M C.Long waves and ocean tides［M］.Evolution of physical oceanography， MIT Press， 1981.

［13］ Accad Y， Pekeris C L.Solution of the Tidal Equations for the M2 and S2 Tides in the World Oceans from a Know ledge of the Tidal Potential A lone［J］.The Royal Society， 1978： 235-266.

［14］冯士笮，李凤岐，李少菁，等.海洋科学导论［M］.北京：高等教育出版社，1999.

［15］ Qian chengchun， Shen Yujiang.Distribution of 9 principal tidal constituents and tide prediction for the East China Sea［J］.China OceanEngineering， 2000， 14（04）： 541-548.

［16］钱成春，沈育疆.中国海域潮汐数值预报［R］.2004.

［17］ FRANCO A S.Tide： fundamentals， analysis and prediction［M］.Sao Paulo，Institutode Pesquisas Techologicas do Estado de Sao Paulo， 1981： 171-232.

［18］方国洪，郑文振，陈宗镛，等.潮汐和潮流的分析和预报［M］.北京：科学出版社，1986.

P731.23

A

1672-2469（2017）10-0073-04

10.3969/j.issn.1672-2469.2017.10.020

2017-03-16

刘 潘（1989年-），男，硕士研究生在读。