316L不锈钢槽的小直径铣刀高速铣削工艺研究
2017-12-01毛丹丹陈远玲阙燚彬
毛丹丹,陈远玲,阙燚彬
(1.柳州职业技术学院 机电工程学院,广西 柳州 545006,2.广西大学 机械工程学院,广西 南宁 530004)
316L不锈钢槽的小直径铣刀高速铣削工艺研究
毛丹丹1,陈远玲2,阙燚彬1
(1.柳州职业技术学院机电工程学院,广西柳州545006,2.广西大学机械工程学院,广西南宁530004)
通过多因素正交实验方法,借助SPSS软件建立316L不锈钢窄槽小直径铣刀高速铣削的最大切削合力回归经验公式,可以对高速铣削316L不锈钢窄槽加工所选刀具(小直径)的铣削合力进行提前估算。论文介绍了具体方法和步骤,所得回归经验公式通过了显著性验证。
小直径铣刀;高速铣削;316L不锈钢;切削力;经验公式
0 引言
316L不锈钢是淡化海水工程领域设备所用液压元器件的常用材料,由于较强的黏附性和铣削时产生的较大冲击、振动,铣刀的损耗非常严重。当前,不锈钢窄槽的小直径高速加工技术,国内外学者鲜有研究。所以,通过进行316L不锈钢窄槽的小直径铣刀进行高速铣削的加工实验并得出切削力回归经验公式,对优化不锈钢窄槽加工的切削参数、提高其加工效率和降低加工成本等方面具有重要的意义。
1 实验条件
1.1 加工设备
实验选用主轴最高转速为24 000 rpm的Fanuc加工中心机床(见图1所示);选用刃口直径为2 mm,刀柄直径为4 mm的钛铝涂层钨钢硬质合金平底铣刀(两刃)。
1.2 数据采集设备
数据采集设备包括电荷放大器(YE5850)、压电式铣削测力仪(YDX-III9702)、数据采集软件数据采集卡和计算机组成。选用的铣削测力仪可测出任意方向力的三个相互正交的分量,具有高灵敏度、高刚度、高固有频率等特性。
设备使用要求:测试前,首先给电荷放大器(见图2)和测力仪设置地线,并参照说明书结合实验数据对电荷放大器进行调试,选择适当的量程和档位。由于进行的是小直径刀具(两刃)小切深高速铣削实验,所测数据应在100 N以内,通过公式换算,数据采集软件选取5 kHz的采样频率。

图1 加工中心(Fanuca-t14iFlb)

图2 电荷放大器(YE5850)
1.3 实验材料
实验材料为316L不锈钢,尺寸规格:120 mm×70 mm×48 mm。
2 槽加工实验方案及数据处理
2.1 槽加工实验方案
根据分析确定对3个切削参数(切削速度、进给速度、轴向切深)对工件切削合力产生的影响通过正交实验和回归分析法进行研究[1]。实验选用四因素三水平实验,实验参数如表1及表2(27组)所示,为得到科学的不锈钢窄槽的小直径铣刀高速铣削的切削合力回归模型,因素的水平是通过单因素实验选定的。
表1 槽加工同侧铣正交实验参数表

因素 水平 切削速度/V轴向切深/Ap每齿进给量/Fz18000600102100008001531200100020
2.2 数据处理方法
由三向石英测力仪测得X,Y,Z方向的切削合力信号,每组参数组合进行3次重复铣削实验(铣削方式为顺序),最终将3次实验值取平均得到切削合力值[2]。
3 实验结果
根据单因素分析及正交实验表选定原则,决定选用四因素三水平L27(313)正交实验表,依次单独进行槽加工实验,研究切削参数对切削合力的影响,最终建立铣削力的回归经验公式[3]。实验参数以及实验分析结果如表2所示。
表2 槽加工L27(313)正交实验参数安排表及实验结果分析

试验号A/VB/Ap空白列空白列C/Fz空白列空白列B×C-1空白列空白列B×C-2空白列空白列合力F111111111111112979211112222222224142311113333333334794412221112223335729512222223331115865612223331112224507713331113332226100813332221113335805913333332221114141102123123123123360911212323123123149251221233123123125087132231123231312508914223123131212363281522313121232316398162312123312231672417231223112331250691823123122311236148193132132132132277220313221321321338822131323213213214319223213132213321488923321321332113248582432133211322134633253321132321213477826332121313232150262733213212131324451K144063651426740804115K249384830459043404610K339614824444848854581
注:A为切削速度,B为轴向切深,C为每齿进居量。
4 回归模型经验公式的建立
假设变量y与x的关系设为P次多项式,则多项式的模型为:
yi=β0+β1xi+β2xi2+…+βpxip+εi(i=1,2,…,n)
(1)
用不同的线性项来替代非线性项,就可通过多元线性回归分析来解决。即令
xi1=xi,xi2=xi2,…,xip=xip则式(1)化为
yi=β0+β1xi1+β2xii2+…+βpxiip+εi(i=1,2,…,n)
(2)
多元多项式回归问题同样也可以通过转化为多元线性回归问题来解决。
本文中,由于事先分析铣削合力与切削速度、进给速度、轴向切深的指标之间的回归曲线类型未知,因此,决定先采用多项式逼近,建立完全二次多项式模型

(3)
其中y为实验的合力值F,xi(i=1,2,3)为实验的3个考察指标因素;系数βi表示xi的线性效应,βii表示xi的二次效应,βij表示xi与xj的交互作用效应。
应用SPSS软件统计分析结果,得到铣削合力F与切削速度、进给速度、轴向切深3个因素的回归模型:
y=-349.24+4.07x1+3 920x2+5 335.67x3-0.021x12-16 445.83x22-64 183.33x2x3
(4)
为了进一步验证该模型能否准确描述变量y与3个因素的关系,还需对回归模型(4)以及各个变量进行显著性检验[4]。
5 回归模型的显著性检验
前面所建立的经验概率模型,区分不了实验过程中由于实验条件的改变而导致实验误差引起的数据波动,对实际结果的拟合程度需采用方差分析对该模型进行显著性检验。方差分析基本思想是将总的离差平方和QT分解为回归平方和QA和剩余平方和QE两部分来构造F统计量,并作F检验,从而判断各因素对实验结果的作用是否显著。
(5)
(6)
(7)
F表达式为:
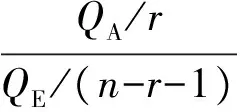
(8)
其中:n代表实验组数,r代表实验因素个数,根据实验安排,已知n=27,r=3。
代入运算式(5)—式(8)可得显著性检验结果如表3所示。
表3 回归模型显著性检验表

模型平方和自由度均方FP回归20685226344754129600000残差5320212026601总计260054226
模型的决定系数R2=0.795,说明y的79.5%可以由模型确定。
回归模型的F统计量=12.96gt;F0.01(6,20)=3.87,显著性检验的P值=0.000,远小于显著性水平0.01,说明所建立的切削力的经验预测模型显著,能够较好地预测切削力。
然后,对模型中各个变量的系数进行显著性检验,得到表4所示结果。
表4 回归模型系数显著性检验表

模型非标准系数标准回归系数BStdErrorBetatP常数项-34924163731-54800000转速(x1)40661055676638560001切削深度(x2)3920000873460652344880000进给量(x3)53356671215663222043890000x2x3-6418333314888767-2705-43110000x12-00210005-6983-39800001x22-164458335263974-4390-31240005
表5 预测模型误差分析表

试验号试验值F/N预测值F/N误差值误差/%1297932823031018241424025-117283347944767-027056457295234-495864558655334-5319056450754359282059761005870-230378858055328-477821941414787646156010360938732647311149254615-3106291250875358271532135089582473514451463285925-4036371563986025-3735821667246460-264392175069591985016771861485378-770125319277227870150562038823530-3529072143194272-0471092248894739-1503072348584839-0190382446334940307663254778537559712492650264833-1933832744514292-159357
从表4可知,各个变量的显著性检验的P值均小于0.05,各个变量都显著。进一步说明了建立的模型的合理性。
运用切削合力回归模型计算预测值,比较该模型的预测值与实际实验结果误差如表5所列。从误差分析表可以看出,有20组参数组合预测误差均限制在10%的范围以内,有6组参数组合预测误差限制在10%~16.8%的范围,可见本文所建立的切削合力预测模型预测较为准确稳定,可以用于316L不锈钢槽加工切削合力的预测。
6 结语
本文通过正交实验,建立了顺铣316L不锈钢窄槽的铣削小直径高速铣削合力经验公式,并进行了显著性验证。所得公式可以对加工生产中所选刀具(小直径)高速铣削316L不锈钢窄槽的铣削合力进行提前估算,对优化316L不锈钢窄槽的铣削工艺参数、提高窄槽加工效率、降低加工成本有重要参考意义。
[1]王庭俊.不锈钢的车削加工[J].金属加工(冷加工),2008(2):89-91.
[2]白琨.超高速切削加工及其关键技术[J].新技术新工艺,2009(9):63-65.
[3]陈锦江,孙博,季景兰,等.基于NSGA-Ⅱ算法的高速铣削参数多目标优化[J].机床与液压,2016,44(19):56-58,177.
[4]张宝磊,熊艺文,王为庆,等.高速铣削TC4表面粗糙度预测模型研究[J].组合机床与自动化加工技术,2015(3):108-110.
2017-08-23
[责任编辑姚胜勋]
SmallDiameterCutterwithHighSpeedMillingCuttingResearchGrooveof316LStainlessSteel
MAODandan1,CHENYuanling2,QUEYinbin2
(1.CollegeofMechanicalandElectricalEngineering,LiuzhouVocationalamp;TechnicalCollege,Liuzhou,Guangxi545006;2.CollegeofMechanicalEngineering,GuangxiUniversity,Nanning,Guangxi530004,China)
This paper holds that through multi-factor orthogonal experiment,using SPSS software to establish a narrow groove small diameter stainless steel 316L high-speed milling cutter maximum cutting force regression empirical formula,high speed milling can be 316L stainless steel narrow groove processing the selected tool (small diameter) of the milling force can be estimated in advance. The paper introduces specific methods and steps,and passes a significant validation.
small mill;high-speed milling;316L stainless steel;cutting force;empirical formula
TH16
A
1672-9021(2017)05-00087-06
毛丹丹(1981-),湖南平江人,柳州职业技术学院机电工程学院讲师,工程硕士,主要研究方向:机械设计与制造。
医疗器械及海水淡化工程所用316L不锈钢的高速切削研究(KY2016LX516)。
