面向供应链追溯的RFID路径编码策略研究
2017-12-01杨乐川杨仙佩张海艳廖国琼江西财经大学信息管理学院
杨乐川 杨仙佩 张海艳 廖国琼 江西财经大学信息管理学院
面向供应链追溯的RFID路径编码策略研究
杨乐川 杨仙佩 张海艳 廖国琼 江西财经大学信息管理学院
随着无线射频技术(RFID)在供应链领域的广泛应用,产生了海量的对象位置移动的路径信息。如何对这些路径信息进行有效编码以支持路径追溯查询是RFID系统面临的挑战性问题。RFID路径编码策略主要分为素数编码和复合编码两大类。素数编码主要用于对路径的位置信息进行编码,复合编码则是在素数编码的基础上,引入区间编码对时间信息进行编码,实现面向时间的路径追溯。本文主要对RFID路径编码策略进行分析和讨论,并指出未来研究方向。
RFID 供应链 路径编码
1 引言
供应链是指产品生产和流通过程中所涉及的原料供应商、生产商、分销商、零售商以及最终消费者等环节通过上下游成员连接组成的网络结构。由于供应链中存在大量移动物品,故会产生海量路径信息。而RFID技术拥有自动快速扫描、穿透性无屏障识别等特点,故RFID技术已广泛应用于供应链物品跟踪与监控,可有效提高管理效率及降低运营成本。同时,RFID数据存储与管理也逐渐成为一个研究热点,如何对RFID路径信息进行有效编码以支持路径追溯查询是RFID系统面临的挑战性问题,近年来得到学者们的关注,并取得了一定研究成果。
通常,衡量一个编码策略性能主要考虑因素包括:1)查询效率。查询速度要尽可能快,查询响应时间尽量要短;2)更新代价。更新代价指的是在对编码树进行插入、删除结点时,对时间空间的开销。好的编码应使各个结点要相互独立,从而使得更新某一个结点时,对其他结点影响尽量少,且更新速度尽量快;3)存储空间。存储空间指的是编码的码值长度以及编码表的硬盘存储开销。由于供应链环境中的RFID数据具有其自身的特点,在进行编码时,还需考虑以下特殊问题:
①环路问题。供应链中的编码对象多为位置信息,但商品在供应链中流通时,可能经过同一个位置多次,于是形成了环路,因此编码应考虑环路情况。
②溢出问题。RFID供应链会产生海量的时空信息,对于编码而言对应的就会产生大量的结点。若编码容量过小,则可能导致结点的码值超出其规定的数据类型。因此,良好的编码应具有较大的编码容量。
③实时更新问题。对象在供应链环境中移动时,其路径是实时产生的,因此良好的编码策略应能对路径进行实时更新,随到随编。
本文将对已有RFID路径编码策略进行分析和讨论,具体介绍其基本实现原理,并分析其优缺点。
2 素数编码
2.1 素数编码基本原理
素数编码(prime_label)是一种充分利用素数唯一性和独立性的编码方式,其具体编码原理为:①在一棵编码树中自顶向下为每个结点指定唯一素数(self_label);②每个结点的prime_label值为其父结点的prime_label值与self_label值的乘积(根结点的prime_label为1);③用叶子结点的prime_label值作为该路径的编码值。
在素数编码中,利用素数的特性引进了两个定理:
定理1 算术基本定理。任何大于1的自然数都可以由有限个且唯一的素数相乘得到。
定理2 中国余数定理。假设存在n个素数a1,a2,…,an,则一定存在一个同余值SC使得SC mod a1=1, SC mod a2=2,…,SC mod an=n。
根据定理1,通过将一结点的prime_label因式分解得知到达该结点前经过了哪些结点。根据定理2中的SC值,可以知道路径所经过结点的先后顺序,因此可以利用素数对路径进行编码。
基于素数的路径编码存储形式可记为(Element_enc,SC),其中Element_enc表示该路径中所有位置对应self_label的乘积(即一条路径最后一个结点的prime_label值),SC表示同余值,用于计算每个self_label对应位置的次序。例如,在图1中,三个位置A,B,C的self_label分别是2,3,5。可计算得到该路径的Element_enc值为30,即2×3×5=30;SC顺序编码值为23:23mod2=1;23mod3=2;23mod5=3。通过这两个值,可以还原出一条路径经过的所有结点及其顺序。
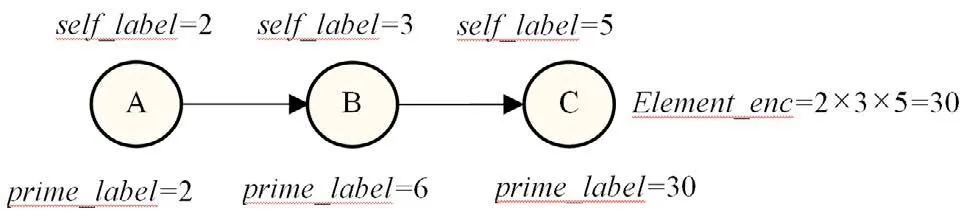
图1 素数编码样例
由于素数编码具有唯一性和独立性,因此更新较为简单。但是,每次更新都需重新计算路径每个结点的SC和Element_enc。在存储方面,尽管存储的是整数,但素数容易溢出,且不能表示环路。
2.2 溢出问题解决方案
当供应链中路径过长时,素数的码值和同余值的数据长度将超过其本身的数据类型长度,我们将这种问题称为溢出问题。
假设存在一条路径,其每个位置的self_label都使用最小素 数 来 编 码:2->3->5->7->11->13->17->19->…->..., 在self_label仅为19的时候,即仅有8个位置长度的路径时,其编码值就达到了2×3×5×7×11×13×17×19=9699690。在实际供应链中,路径数量巨大,且起点与路径总长度各不相同,实际编码的长度将会更大。溢出问题主要以下有两类方法。
2.2.1 利用小素数减缓溢出
文献[9]在素数编码基础上充分利用小素数减缓编码数据的增长速率。对于非叶子结点,它像素数编码一样,为每一个结点都分配一个素数,但不同之处于其素数分配算法优先为根结点的孩子分配较小的素数,其他的结点依次分配除此之外的小素数。因为供应链大批量物品运动时,越靠近根结点在路径中会反复出现,从而在Element_enc中被反复计算,分配小素数给最频繁计算的结点能使码值整体偏小,减缓溢出。
对于叶子结点的编码,使用2的倍数,且兄弟叶子结点的编码是整除关系。这样对叶子结点编码,可以容易计算父结点的编码及判断两条路径有无共同子路径,有利于追溯查询和面向路径查询。在该编码中,由于依次使用小素数,因此也省去了SC值的计算,用素数编码计算出的素数,按大小排序便是每个结点在路径中的顺序。例如,在图2中,编码为3,5,7的结点全部分布在第一层,因为之后的路径都要经过这些位置,所以给他们分配了较小的素数,而结点F的编码值为66=33×21,因为它是其亲代的第一个叶子结点,所以分配2给它而不是23。同时,若一条路径的编码值为260,可将其分解为5,13,2,2。将除2以外数字从小到大排列可知其先后经过了C,B;而有两个2,代表再经过了B的第二个孩子A,由此可推出路径C->B->A。
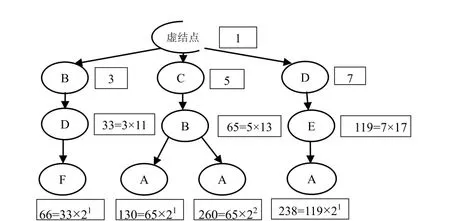
图2 小素数减缓溢出
2.2.2 路径分裂法
为了解决素数的溢出问题,文献[10]中提出了一种路径分裂方法,其基本思想是规定一个最大长度MAX,当路径的Element_enc值超过了MAX值后,将一条长路径分裂成几个片段,使分裂后的路径片段的Element_enc长度小于MAX值,从而将一条长路径分割成多条较短路径,从而缓解溢出问题。
如图3(a)中路径的Element_enc=2×3×5×7×11×13=30030。假定MAX=1000,2×3×5×7=210<MAX;2×3×5×7×11=2310>MAX。因此路径从self_label=7的结点开始分裂,也就是D处,从而得出图3(b)中的两条路径。
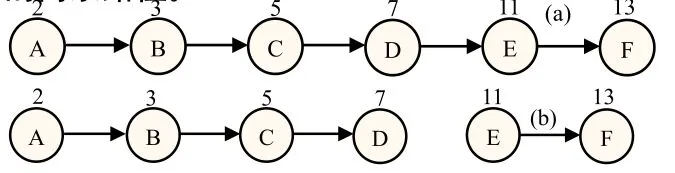
图3 路径分裂法减缓溢出
利用小素数的方法在一定程度上缓解了素数编码的增长速率,但要做到给根结点的孩子分配较小的素数,需要等全部数据到达后再进行编码,难以做到实时更新。虽然路径分裂方法能较好地解决溢出问题,但由于每条路径分裂的次数需计算得出,且可能各不相同,会增加存储表的复杂度与不稳定性,间接影响查询效率,且当路径够长时,单个结点的self_label有可能超出MAX值,导致一个结点一条分路径,此时表的数据会更加冗余。
2.3 环路问题解决方法
设 物 体 经 过 的 路 径 为 L1->L2->…->Ln,若 存 在i,j(1<=i<=j<=n)使得 Li=Lj,则说明路径中至少存在一个环,我们称此类路径为带环路径,反之,称为无环路径。例如,存在 一 条 路 径 A->B->C->A->C->A。可 以 看 出,L1=L4=L6,L3=L5,构成了一个复杂的嵌套环路。由于素数编码中相同位置的self_label相同,SC值无法计算,因此用原始的素数编码无法描述环路问题。而供应链中编码树结点的海量性,使得在编码中不可避免会遇到环路问题。主要有以下两种解决方法。
2.3.1 结点重命名
文献[11]采用重新命名结方式解决供应链中出现的环路问题,即将物体在不同时间到达的同一个结点看成是两个不同的结点,以此来满足各种查询需求,但该解决方法一定程度上加快了溢出的速度,且增加了对带环路径查询的复杂度。
如图4所示,物品重复经过了几次A和C,但由于经过的时间不同,可将A和C当做不同的位置看待。因此图中六个位置的self_label编码依次为2,3,5,7,11,13;Element_enc为30030,SC值为29243。

图4 环路结点重命名
2.3.2 环路编码
对于环路问题,文献[12]提出一种考虑环路的素数编码策略,称为环路编码。其给出了一种新的计算同余值(SC)方法,即将计算SC时除数相同的项合并为一项并把它们的序号(即余数)信息加入到合并后的公式(1)中:

其中primet表示每个位置的self_label,即唯一的素数,kt表示该位置在路径中出现的次数,its表示该位置在路径中的序号。考虑素数编码中可能出现余数大于除数的情况,每个位置分配的素数应大于其在路径中的次序,primet>its。
文献还证明了素数编码是其环路编码的一种特例,并给出了相应的解码方法,以还原出原路径的位置和序号。
例如,如图5所示,C和D重复出现形成环路。A、C、D三个位置的self_label编码依次为2,5,7。路径的Element_enc值为2×5×7×5×7=2450,SC值满足:
SC<Element_enc;
SCmod2=1;
SCmod52=2+4×5;
SCmod72=3+5×7;
于是。可以得出SC=2047。

图5 环路编码示意图
编码(2450,2047)的解码过程如下:
①2450因式分解为2×52×72,得到经过位置A,C,D,且两次经过C和D。
②由SC=2047得到A位置对应序号SCmod2=1,位置C对应序号i1=2047mod5=2,i2=(2047mod52-2047mod5)/5=4。位置D对应序号i1=2047mod7=3,i2=(2047mod72-2047mod7)/7=5。
③还原路径为 A->C->D->C->D.
由以上实例可看出,环路编码可以很好的解决带环路径问题,且整个编码解码的过程中没有信息丢失。
此外,该文献在环路编码的基础上给出了针对长路径编码溢出的路径分裂方法。不同的是,在分裂路径时,对计算每个位置的SC值时,所用的位置结点序号仍是该位置在长路径中的绝对位置序号。
3 复合编码
素数编码是面向路径的编码,只能存储路径位置信息。然而,在RFID供应链中不可避免会遇到面向时间的查询需求。为了应对素数编码在面向时间的编码缺失问题,已有文献给出了面向路径的素数编码和面向时间的区间编码的复合编码模型。
3.1 素数与区间相结合的复合编码
文献[11]提出了一种素数编码和区间编码共同使用的复合编码,分别建立一棵路径树和一棵时间树,即用素数编码方法编码路径的位置信息,用区间编码方法编码路径的时间信息,在区间编码中,使用对编码遍历的方法给每个结点一个start值和 end值(图为后序遍历)。若A.Start<B.Start且B.End<A.End,可以判断A是B的祖先。
例如要对如下路径数据进行编码时,采用复合编码方案,将路径里的位置信息抽出来进行素数编码,将带时间的路径数据进行区间编码,区间编码用后序遍历产生,生成的编码树如图6,图7所示。
A[2,3]->B[5,7]->C[8,9]
A[2,3]->B[5,7]->D[13,16]
A[2,3]->B[7,8]->D[14,18]
A[2,3]->E[6,4]->C[7,8]
A[2,3]->D[4,5]
A[2,3]->D[5,6]
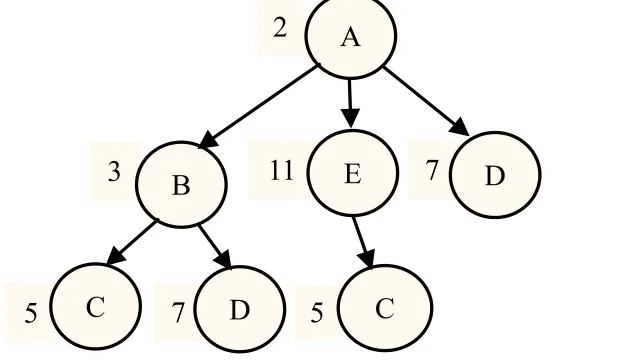
图6 复合编码中的路径树

图7 复合编码中的时间树
查询实例1(不带时间的路径查询):查询经过了B的所有路径。在图7中,B的self_label为3,找到所有能整除3的Element_enc值即可,于是找到了Element_enc值30和42,从而找出路径 A->B->C 和 A->B->D。
查询实例2(带时间的路径查询):查询在5到7时间内经过B点的所有路径。在图8中,B[5,7]的区间编码为(2,7),查询所有结点中Start<2且End>7找到B[5,7]的亲代结点A[2,3],A[2,3]为根节点,停止追溯。再查询所有结点中Start>2且End<7的结点,找到C[8,9],D[13,16],都为叶子结点,停止追溯。由此,查询出路 径 A[2,3]->B[5,7]->C[8,9]和 A[2,3]->B[5,7]->D[13,16]。
区间编码实现了时态信息查询,但是一旦有一个结点发生改变,可能就会导致其它结点要重新编码。如图7中在C[8,9]与D[13,16]之间插入结点X,其编码变为(5,6),替代了原先D[13,16]的编码,使原本的结点码值往后移,整棵树的编码仅有C[8,9]不用变化,其他结点的编码全都要改变,因此更新代价较大。
3.2 DRB编码
为解决上述问题,文献[9]在复合编码的基础上,提出一种改进的区域编码方法“DRB(Durable Region-Based numbering scheme)编码”代替上述区间编码。DRB编码方法使用深度遍历时间树得到一对整数值(order,size)。每条路径的编码只用该路径上最后一个位置的编码来表示。
对于DRB编码有三个性质:
①对于任意一个节点B,若它的父节点为A,则必须满足order(B)>order(A)且 order(B)+size(B)<order(A)+size(A)。
②对于任意两个兄弟节点B和C,若B是C的前驱,则必须满足 order(B)+size(B)<order(C)。
③对于树中的任意节点A,size(A)是一个任意的正整数值,A的孩子集合为B,则必须满足size(A)>=∑B(size(B))。
该编码方法相比较于区域编码方法最大的优点在于它的更新代价更低,它为以后要插入的新的路径结点预留了空间。当新的路径插入时,该路径后面的位置结点不需要重新编码。
如图8中,X结点是待插入结点,按DRB编码的三个性质得出如下不等式:
order(X)>order(B)=10 且 order(X)+size(X)<order(B)+si ze(B)=40
order(C)+size(C)=16<order(X)且 order(X)+size(X)<order(D)=20
size(B)=30>=size(C)+size(X)+size(D)=10+size(X)
化简后可得:
10<order(X);order(X)+size(X)<40;
16<order(X);order(X)+size(X)<20;
size(X)<=20
X的三个可能取值为:order=17 size=1;order=17 size=2;order=18 size=1;但无论是哪一种,在此例中其他结点的码值都不会发生变化,更新代价较小,但当插入位置没有size和order的可行解时,仍会同区间编码一样产生大面积更新。
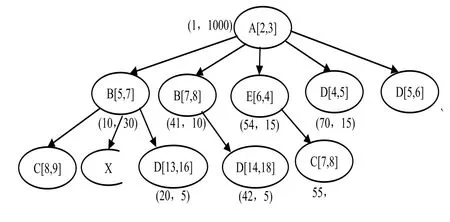
图8 DRB编码
可以看出,与区间编码相比,DRB编码更新性能有明显提升。但由于很难预测新插入的结点需要多大的预留空间,因此可能会导致不必要的空间浪费。
4 工作总结
从目前来看,RFID路径编码中的主要使用的方法有素数编码及复合编码。素数编码在对路径追溯查询时有较好的表现。通过对素数编码的不断完善,解决了长路径溢出问题及供应链中的环路编码问题,使得素数编码能较好的满足供应链中各种面向路径的查询。复合编码方法是在素数编码的基础上引入区间编码,存储路径中的时间信息,能满足面向时间的路径查询需求。但是,由于素数编码和区间编码的更新代价较大,不能较好满足路径实时更新需求,因此需进一步研究更新代价低、支持实时动态更新的路径编码策略。另外,为保证供应链环节的信息保密需求,分布式编码策略也是将来研究方向之一。
[1]Derakhshan R, Orlowska M E, Li X. RFID Data Management: Challenges and Opportunities[C]//Proceedings of 2007 IEEE International Conference on RFID. IEEE,2007:175-182.
[2]Want R. An introduction to RFID technology[J]. IEEE Pervasive Computing, 2006, 5(1): 25-33.
[3]Hector G,Han Jiawei, Cheng Hong,et al. Modeling massive RFID data sets:A gateway-based movement graph approach[ J].IEEE Transactions on Knowledge & Data Engineering, 2010, 22(1): 90-104.
[4]Wang Y, Zhang G, Sheng F, et al. A RFID data cache structure based on Dual T-Tree for spatio-temporal query[C]// Proceedings of the 4th International Conference on Information Science and Technology. IEEE, 2011:357-362.
[5]刘敏,李战怀,陈群,智能超市中在线与离线 RFID数据仓库技术研究 [ J]. 计算机工程与科学,2011,33 (11):171-176.
[6]Lee C H, Chung C W. Efficient storage scheme and query processing for supply chain management using RFID[C]// Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. ACM,2008: 291-302..
[7]Wu W, Guo W, Tan K L. Distributed Processing of Moving K-Nearest-Neighbor Query on Moving Objects[C]//Proceedings of the 23rd International Conference on Data Engineering. IEEE, 2007:1116-1125.
[8]Li Q, Moon B. Indexing and Querying XML Data for Regular Path Expressions[C]// Proceedings of the 27th VLDB Conference, Roma:University of Arizona.2001:0.
[9]伏楠, 郑丽英, 朱宇航. RFID路径数据编码压缩存储技术研究[J]. 兰州交通大学学报, 2013, 32(1):82-87.5.
[10]陈雄, 王笑梅. 基于素数编码技术对供应链中路径编码的研究[J]. 上海师范大学学报(自然科学版), 2012, 41(5): 483-489.
[11]Lee C H, Chung C W. RFID Data Processing in Supply Chain Management Using a Path Encoding Scheme[J]. IEEE Transactions on Knowledge & Data Engineering, 2011,23(5): 742-758.
[12]Lu Y, Chen L. An improved RFID data encoding scheme for cycling path problem[C]// Proceedings of the 4th IEEE International Conference on Software Engineering and Service Science. IEEE, 2013: 611-615.
本研究受江西财经大学大学生创新创业训练计划项目(201710421025)和江西省自然科学基金项目(20151BBG70046)项目资助。
