局部均值伪最近邻算法在降水预报中的应用

林润生,黄明明

(北京市气象信息中心,北京 100089)

局部均值伪最近邻算法在降水预报中的应用

林润生,黄明明*

(北京市气象信息中心,北京 100089)

分析北京地区日降雨量资料发现,相较于其他降雨事件,大雨或暴雨事件发生的次数较少,因此该地区的降水量预报属于样本不均衡问题.在样本不均衡的情况下,K最近邻算法的分类误差率将会大大提高,这也就使传统的基于K最近邻算法的降水量预报方法的应用受到了限制.针对北京地区降水量预报这一样本不均衡问题,应用局部均值伪最近邻算法构建了北京市的降水量预报模型.该方法利用北京地区日降雨量资料和美国国家环境预报中心全球格点资料,将降雨量作为类,将美国国家环境预报中心全球格点资料的各种因子场作为天气样本特征,计算得到不同天气样本在所有类中的局部均值伪最近邻,通过决策规则实现最优分类.利用提出的降水预报模型对北京市2010年6-8月进行了24 h降水预报,实验结果表明,提出的预报方法对于降水等级预报的预报准确率以及晴雨预报的TS评分、正样本概括率、空报率和漏报率均优于传统的K最近邻预报方法,该方法具有较好的预报效果.

局部均值伪最近邻算法;K最近邻算法;降水量

降水是影响气候的主要因素之一,它对农业、能源产业以及社会和经济的发展具有至关重要的作用,并且也为各物种提供了一个稳定的栖息地[1-5].然而,短期强降水通常会导致洪水、山体滑坡和城市洪涝等严重灾害,给人们的经济和生命财产安全造成巨大损失[6].因此,精确的短期降水预报对于防灾减灾,保护人民群众的生命财产安全和维护社会稳定具有重要作用.但是天气形势复杂多变,特别是降水天气的产生极为复杂,降水被认为是天气预报中最重要也是难度最大的一项[7].因此,如何提高降水预报的准确度也是研究者们一直关注的热点问题.

刘还珠等[8]应用MOS(Model Output Statistics)数值预报产品释用方法建立方程,制作了温度、风、降水、云量、相对湿度和能见度等气象要素预报,但预报检验结果显示降水预报尚未达到可用程度,需加以改进.邵明轩[9]利用KNN算法从历史样本集中搜索出近邻子集,并根据近邻子集做出未来天气预报.翟宇梅[10]提出了一种制作概率天气预报的K近邻非参数估计仿真模型(简称KNN-M),利用该模型进行了云量和降水的概率预报试验.闵晶晶等[11]在传统BP算法的基础上,提出一种改进的BP算法进行降水预报.该方法在网络训练过程中自动确定最优的学习训练和网络结构参数,并利用这一方法建立江淮流域68个站24 h降水3个等级的预报.范严等[12]为提高降水预报的准确率,提出模糊聚类算法来构建降水预报模型.该方法根据空气的流动特性,采用模糊聚类算法分析预报因子的内部特性来表述预报因子间的联系,构建初始预报模型,并根据最小二乘回归方法训练得到降水预报模型.邓小花等[13]应用支持向量机(SVM)方法分别建立海水浴场不同预报时效内的气温、降水和能见度预报模型,使预报准确率得到提高.

综上易见,K最近邻(K-Nearest Neighbor,KNN)算法[14]被广泛应用于天气预报中.事实上,KNN算法过程简单、有效而且易于理解,属于一种非常简单有效的分类方法[15].此外,基于KNN算法的天气预报方法即K近邻预报方法不需要建立预报方程,可避免建立预报方程时所需作的种种假设以及假设和实际不一致时产生的误差,是一种稳定的预报方法[16].然而,研究表明[17-18],在不平衡样本以及样本集受到离群点的影响时,KNN算法的分类误差率较高.此外,KNN算法对于近邻点个数也就是K值大小的选择较为敏感.目前在气象领域中,在处理不平衡气象数据集的天气预报问题上,应用KNN算法进行降水预报的研究较为少见.陈凯等提出了基于加权的KNN算法,采用权值的方法来改进在不平衡数据集中的预报性能.曾晓青[16]考虑了小概率事件的天气如强降水与无降水事件的样本数不均衡的情况,在选择K近邻域时,分别考虑两类不同天气的样本,通过交叉检验方法,分别获取有天气事件的正样本值和无天气事件的负样本值,从而有效的确定了K值的最优组合.并利用这一方法制作了不同站点的晴雨预报和不小于10 mm的降水预报,使得降水预报评分得到提高.然而,该方法仅对降水样本类别数是两类的情况适用,不是普遍适用的,不适用于本文的降水量预报,具有一定的局限性.因此,对于降水量样本集不均衡的问题,选取合适的机器学习算法来进行降水量的分类,制作降水量预报,是本文的研究重点.

局部均值伪最近邻(Local Mean-based Pseudo Nearest Neighbor,LMPNN)算法[19]是在KNN算法基础上提出的一种新的机器学习算法.研究表明[19],与KNN算法相比,在不平衡样本以及样本集受到离群点的影响时LMPNN算法具有较低的分类误差率,分类性能较好.此外,LMPNN算法对于K值的选择鲁棒性更强.因此,本文应用局部均值伪最近邻算法构建北京市降水量预报模型,并利用该模型制作了北京地区的降水量预报试验.实验结果表明,应用局部均值伪最近邻算法的降水量预报方法的预报效果比传统的K最近邻算法有明显的提高,该方法具有较好的降水量预报能力和预报准确率.

1 基于KNN算法的降水量预报模型简介

通常情况下,给定一组输入和输出数据(X,Y),参数估计方法通过拟合寻找函数的具体关系式:

其中α是模型参数,拟合的过程就是在全部训练数据集对(xi,yi)样本上最小化准则函数J(α).模型建立后,可以利用这个模型计算新的输入数据x～的输出估计值y～.与参数模型相比,KNN算法属于非参数估计技术,基于KNN算法的降水量预报模型不关心公式(1)中函数g的具体形式,而是在全部训练数据对样本集也就是历史降水样本数据集(xi,ci)(ci是降水样本xi的所属类别)上寻找关于待预报样本x～的k近邻子集待预报降水样本被分类为k近邻子集T中出现最多的那个类别,如公式(2)所示.

若

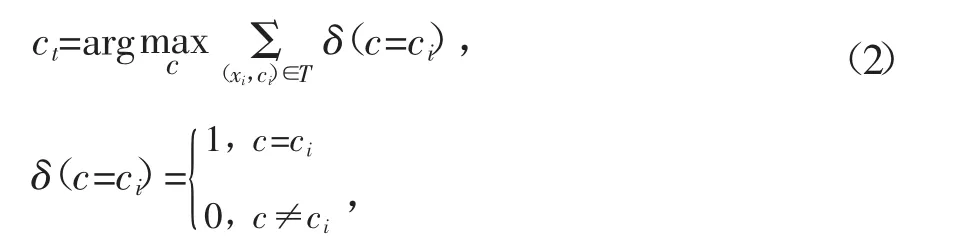
则x∈ct.

研究表明[20-21],基于KNN的分类算法都是以训练样本集合中类分布基本平衡为假设前提的,在不均衡数据集上的分类效果倾向于多数类.曾晓青在文献[16]中也指出,对于有无降水来说,有无中雨或有无大雨等类型的天气样本数是不均衡的,特别是在北方地区.因此,对于北京市降水量预报这一降水量样本不均衡的问题,基于KNN算法的降水量预报方法将导致待预报日的降水量类别预报(分类)错误.如图1所示,以历史降水样本集合中包含无雨和暴雨两个降水量类别为例.显然,相较于无雨类别,暴雨类中包含的样本数量较少,即降水量样本集的分布是不均衡的.由图1可见,根据基于KNN算法的降水量预报模型即公式(2)计算可得,待预报降水样本属于降水样本较多的无雨类.然而,该预报样本事实上应该属于暴雨类.因此,样本数量的严重不均衡导致了KNN分类器判别错误.

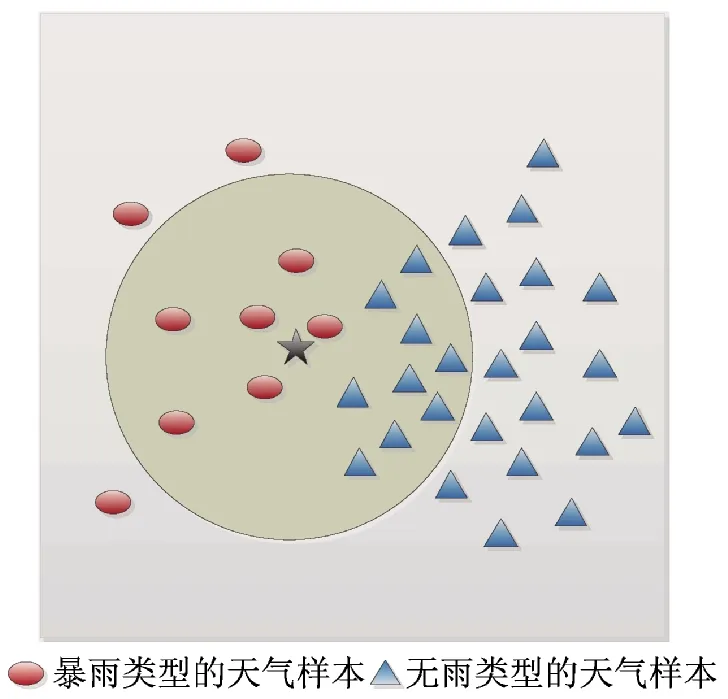
图1 不均衡数据集上的基于KNN算法降水量分类

2 局部均值伪最近邻算法在降水量预报中的应用

针对降水量预报中历史降水样本集不均衡问题,本文将局部均值伪最近邻算法用于构建降水量预报模型.局部均值伪最近邻算法首先在历史降水样本集的每一类别中寻找待预报降水样本的k个近邻样本,然后计算这k个近邻样本的局部均值向量,并分别赋予这k个局部均值向量不同的权重,最后根据待预报降水样本的k局部均值向量得到该待预报降水样本的伪近邻来进行分类.下面首先介绍基于LMPNN算法降水量预报模型所用到的资料,然后给出LMPNN算法,最后应用LMPNN算法构建北京市降水量预报模型.

2.1 资料

基于LMPNN算法的降水量预报模型的历史降水样本集采用的降水实况数据集和因子场资料如下所示.

(1)本文采用的降水实况数据集来源于北京市气象信息中心提供的20个国家站2006-2010年6-8月北京市逐日20:00到次日20:00的24 h降水量实况.将实况集中的样本按照降水量进行分类,分别把无雨、小雨、中雨、大雨、暴雨五类标记为{0,1,2,3,4}.由于气象部门的降水量分类类别太多,且不同降水量类别有重叠现象,本文采用了防汛部门的24 h降水量划分法来对降水量进行划分,具体划分标准见表1.

表1 降水量等级划分

(2)因子场资料选取的是2.5°X2.5°的美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)全球格点资料,利用NCL软件读取地面和高空1000～50 hPa资料,范围为107.5°～125°E,30°～47.5°N,包括温度场、位势高度场、径向风速场、湿度场、地面可降水量场.

预报因子场范围和预报因子的好坏直接影响预报效果,参考文献,本文最优预报因子场范围和因子的选择如下:

考虑到预报地北京市的地理位置(东经116.3°,北纬39.9°),选取以北京为中心,范围为12.5～12.5经纬度(即112.5°～120°E,35°～42.5°N,总共4X4个格点)作为最优因子场的范围.

选取的预报因子如表2所示.为了避免各项预报因子量级的差异,对预报因子进行归一化处理,从而达到消除不同单位和量纲影响的目的[22-23],归一化公式如下所示.

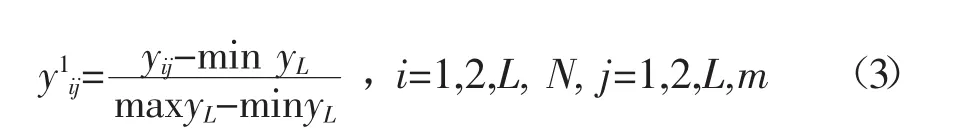
表2 降水预报选取的预报因子

2.2 局部均值伪最近邻算法

(1)计算测试样本x与类ωi,i=1,2,……M的类子集Tωi中各样本的欧式距离,即d根据该距离获得测试样本在Tωi中距离最近的k个训练样本,并将这k个训练样本按照其与测试样本x的距离由小到大的顺序排列,记为

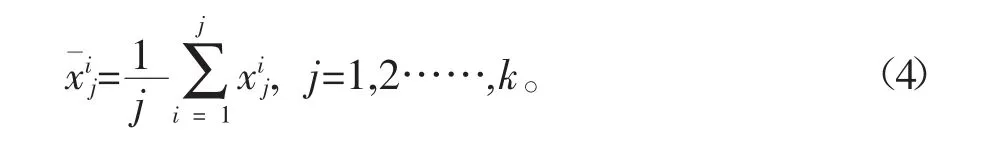
(4)设测试样本x在类ωi,i=1,2,…,M中的局部均值伪近邻(Pseudo Nearest Neighbor,PNN)是满足如下约束函数

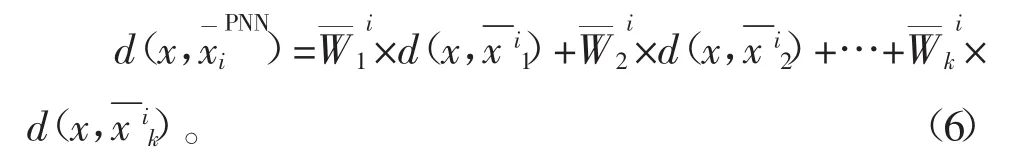
(5)定义ωi,i=1,2,…,M类的判别函数是f(ix)=d,决策规则为:若

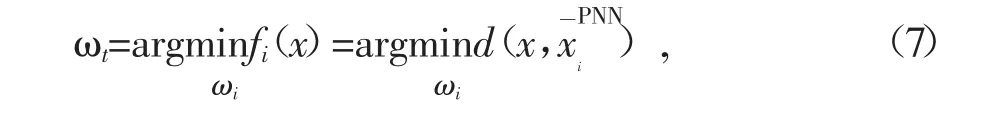
则决策x∈ωi.

显然,由LMPNN算法的步骤(1)可知,不同于传统KNN算法在整个训练样本集即历史降水样本数据集里搜索k近邻,LMPNN算法在每类训练样本集合里搜索k近邻,考虑了未分类样本在每类训练样本里的最近邻信息,这也就采用了分而治之的思想来降低训练样本集上样本分布不均衡对正确分类造成的影响.由LMPNN算法的步骤(2)、步骤(3)和步骤(4)可知,该算法在每类训练样本集合里搜索得到k近邻后,计算这k个近邻样本的局部均值向量,这也就充分利用了每类训练样本集的整体均值信息.特别是根据待预报降水样本与这k个局部均值向量距离的远近来添加不同权值,这又进一步采用权值的方法来改进在不平衡数据集中的预报性能.因此,应用该局部均值伪近邻算法构建北京市降水量预报模型将会提高该地区降水量预报的预报效果.

2.3 基于局部均值伪最近邻算法的降水量预报模型

应用LMPNN算法构建的北京市降水量预报模型可表述如下:

用xi,i=1,2,…,n表示第i个历史降水样本,采用上文3.1节选取的预报因子作为该样本的特征,即xi=(xi1,xi2,…,xim)其中xij表示第i个样本的j个气象因子,xij是利用公式(3)进行归一化处理后的因子值.此外,yi,i=1,2,…,n表示样本日第二天的降水量类别yi∈{0,1,2,3,4}.因此,基于LMPNN算法的降水量预报模型的历史降水样本集如式(8)所示,该样本集包括M=5类.

另外,给出待预报样本如公式(9)所示,

基于LMPNN算法的降水量预报模型可表述为:

若

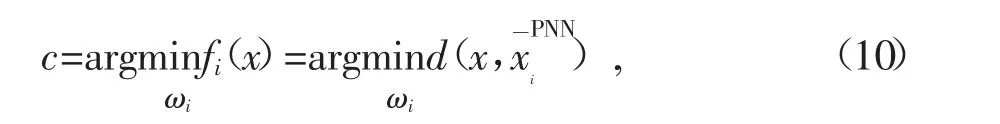
则预报结果是x∈c.

本文提出的基于局部均值伪最近邻算法的降水量预报模型中需要确定的参数是k,也就是待预报样本搜索得到的近邻样本的个数.在k值的选择中,采用交叉验证的方法获取最优k值.首先确定某一k值,本文从k=1开始.把训练样本平均分成10份,取训练样本中一部分(占训练样本的29%)作为试预报样本集即测试样本集,剩余部分作为训练样本集(占训练样本的71%),通过不断地交叉更换预报样本,直到遍历整个样本集为止.然后再改变k值,重复上述过程,直到k值实验完毕.事实上,由2.1节所述的LMPNN算法易知,k值应小于等于所有训练样本类中含最少样本类中的样本数目值即k≤min{Ny}i=1,2,…,M.

对于上述预测结果采用2种评分标准,分别是准确率和TS评分:

TS(Threat Score)评分是目前国内外降水评估最常用的一个评判工具[24].为了取得较好的预报效果,既考虑总体样本的准确率,又要考虑TS评分.本文提出如下k值选择公式:

经过交叉验证,选出准确率和TS评分都达到最优的k值也就是说使得公式(13)中(1-准确率)与(1-TS)的和取最小值时对应的k值作为最优k值.

3 实验结果与分析

本文以北京地区6、7、8月的降水量为研究对象,以2006-2009年6-8月的数据作为训练样本,以2010年6、7、8月的24 h降水量为测试样本.根据2.3节所述的应用局部均值伪最近邻算法构建的降水量预报模型,制作2010年6、7、8月的逐日24 h降水量预报实验.本实验在Eclipce3.7.2下采用Java语言编程实现,硬件环境为Inter Core i7-6700 CPU 3.40GHz.

首先由2.3节所述的k值选择方法,通过交叉验证方法,交叉变换训练样本中的测试样本集,选出准确率和TS评分都达到相对最优的k值即k=5.然后根据选取的最优k值,制作2010年6、7、8月的逐日24 h降水量预报.为了直观反映本文应用LMPNN算法构建的降水量预报模型的预报效果,并与传统的基于KNN算法的降水量预报模型进行比较,制作2010年6-8月的实际观测和预报降雨量的降水量预报效果图,如图2、图3和图4所示.为了公平起见,基于传统KNN算法的降水量预报方法的因子场采用与本文提出的降水量预报方法相同的因子场如本文2.1节所述.

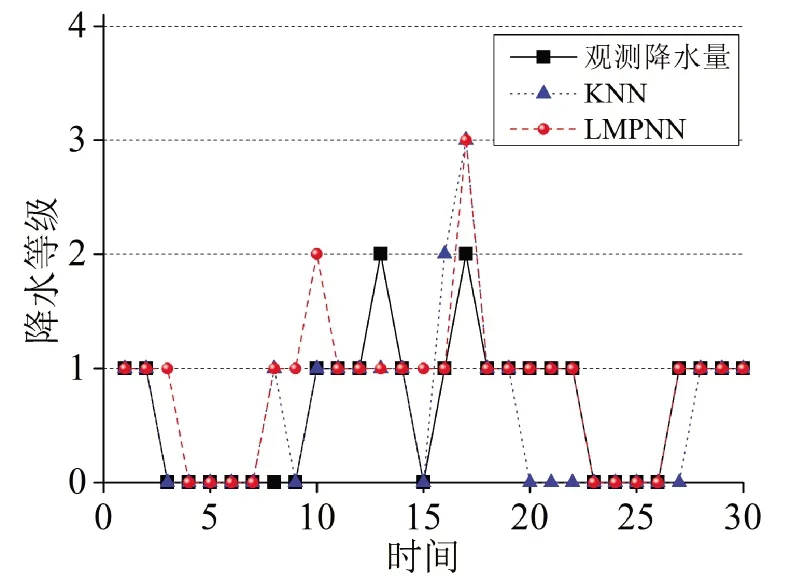
图2 2010年6月两种预报方法的预报效果及观测降水量

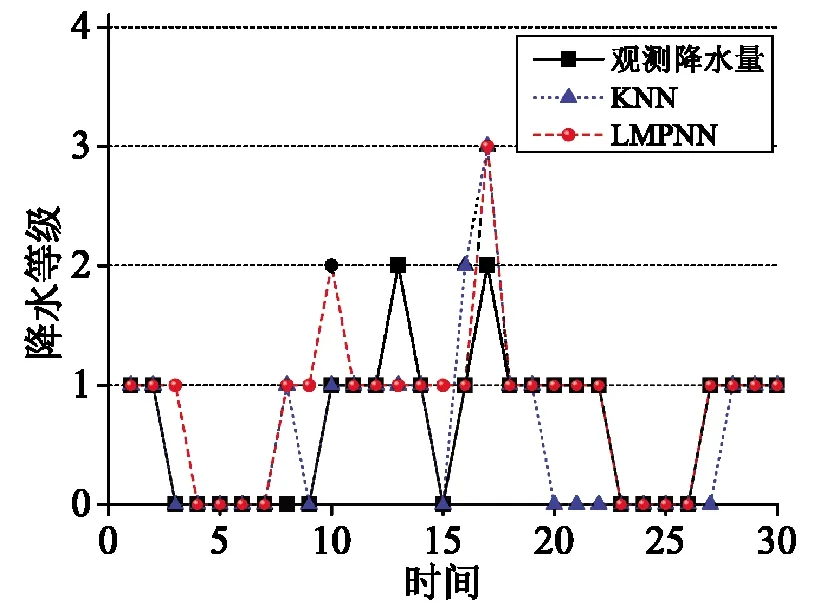
图3 2010年7月两种预报方法的预报效果及观测降水量

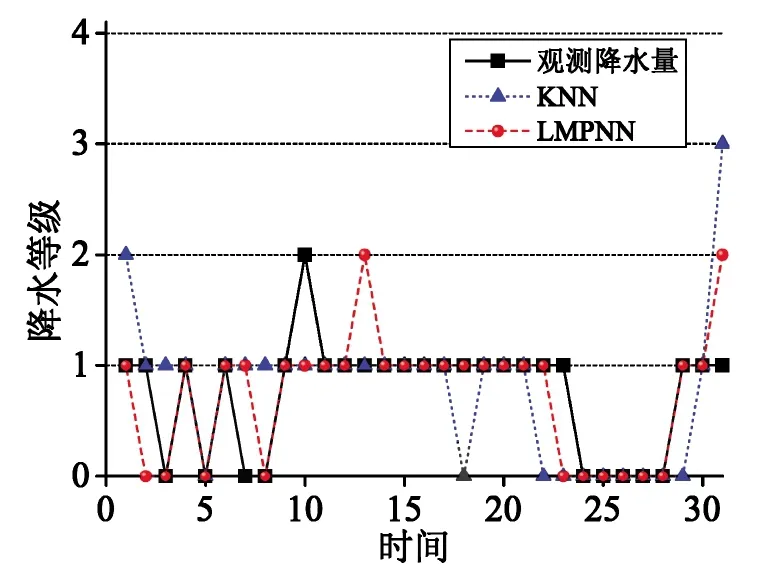
图4 2010年8月两种预报方法的预报效果及观测降水量

由图2～4分析得到2010年6-8月北京地区两种降水量预报方法的预报准确率如表3所示.由表3可见,相比传统的基于KNN算法的降水量预报方法的准确率,基于LMPNN算法的降水量预报方法的准确率分别高出3.34%,12.91%,12.91%.由分析结果可以看出,本文提出的基于LMPNN算法的降水量预报方法具有较好的预报效果.此外,对2010年6-8月北京地区的降水样本进行了统计,统计结果显示,2010年6-8月并无暴雨样本,因此本文对降水样本中无雨、小雨、中雨、大雨这4个等级进行了预报,如表4所示.由表4可见,基于LMPNN算法的降水量预报方法的等级预报准确率和晴雨预报的TS评分略高于传统的基于KNN算法的降水量预报方法.由晴雨预报的TS评分公式(12)可知,对于无雨这一降水量级,该等级中的样本均是负样本即无雨的情况而没有正样本,因此,对无雨这一等级进行晴雨预报时TS评分应均为0%,如表4所示.

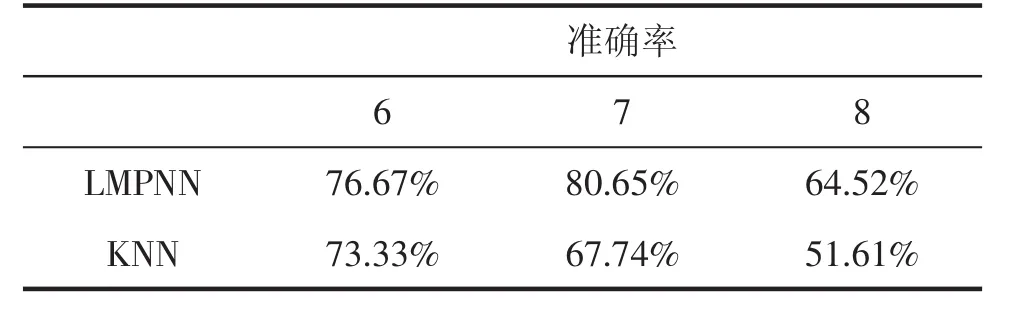
表3 2010年6-8月两种降水量预报方法的预报准确率对比

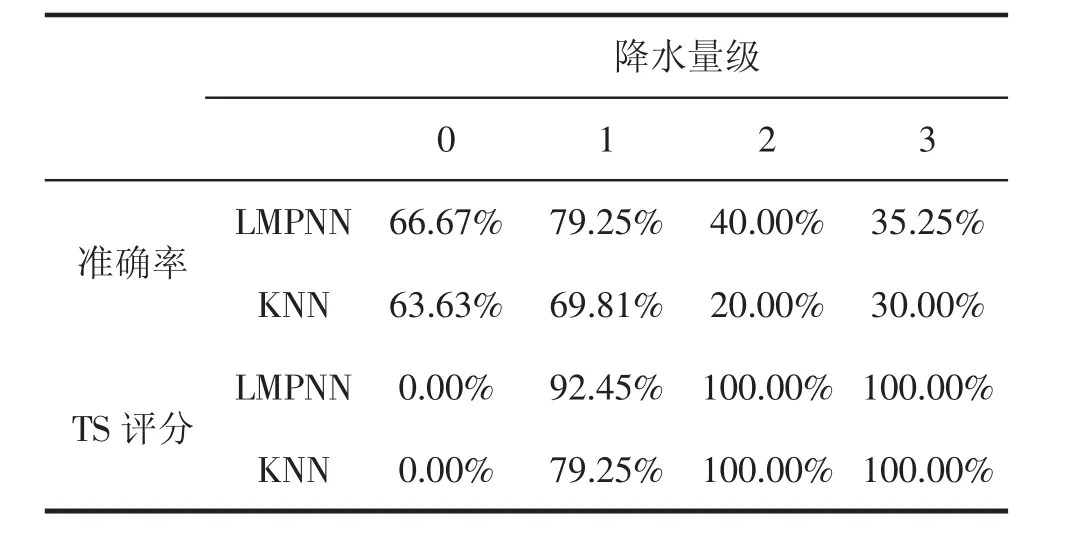
表4 2010年6-8月两种降水量预报方法的分级预报准确率和TS评分对比

为了进一步验证本文提出的降水量预报方法的性能,对2010年6-8月逐日20:00-20:00 24 h降水量进行大于或等于0 mm的晴雨预报.晴雨预报采用国内外公认的降水量预报评价标准TS评分、正样本概括率、漏报率和空报率来评估本文所提出的降水量预报方法的晴雨预报效果.TS评分公式如2.3节公式(12),空报率和漏报率计算公式如式(14)、(15)和(16).

2010年6-8月总共92 d的逐日24 h晴雨预报效果如图5、图6所示.图5、图6是上述两种方法晴雨预报的TS评分、正样本概括率、空报率和漏报率.根据图5的TS评分和正样本概括率结果可知,传统的基于KNN算法的降水量预报方法的2010年6-8月晴雨预报的TS评分和正样本概括率分别是67.14%、79.66%,而本文提出的基于LMPNN算法的预报方法分别为78.57%、93.22%,分别比基于KNN算法的降水量预报方法的评分高11.43%、13.56%.由图6易见,传统的基于KNN算法的降水量预报方法的晴雨预报的空报率和漏报率分别是18.97%、20.34%,而LMPNN方法仅为16.67%、6.78%,分别比传统方法降低了2.3%和13.56%.这也就表明,本文提出的基于LMPNN算法的降水量预报方法在做晴雨预报时,更多地减少了漏报,对空报情况也有所改进.因此,由以上分析结果可以看出,本文提出的应用LMPNN算法构建的北京市降水量预报模型的定量降水预报能力及预报可信度均得到很大提高.

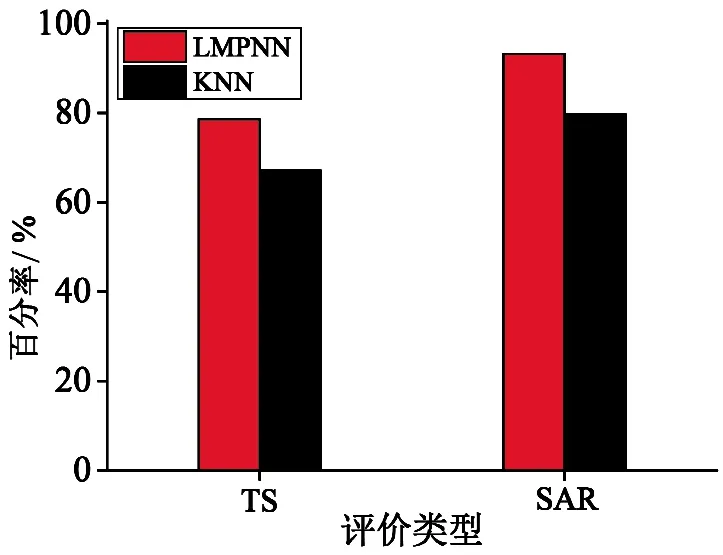
图5 2010年6-8月两种预报方法的TS评分和正样本概括率对比

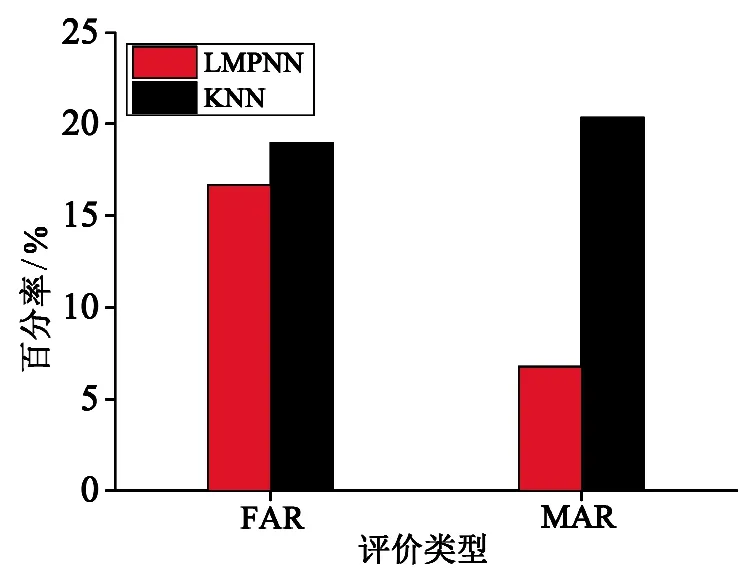
图6 2010年6-8月两种预报方法的空报率和漏报率对比

4 结语

以北京市降水量为研究对象,针对降水预报中降水样本数不均衡的问题,应用局部均值伪最近邻算法构建降水量预报模型,制作了北京地区降水量预报.本文所提出的降水量预报方法对于降水等级预报的预报准确率以及对于晴雨预报的TS评分、正样本概括率、空报率和漏报率明显优于传统的基于KNN算法的预报方法,具有较好的预报效果.此外,本文提出方法的空报率和漏报率均较小,使得预报的可信度得到很大提高.然而,基于LMPNN算法的降水量预报方法选取了与已有参考文献中相似的预报因子场,显然不十分合理,具有很大的局限性.事实上,因子场的好坏直接影响预报效果,有效的预报因子场选择方法有助于提高预报水平.因此,合理的最优预报因子场选择方法是下一步工作中需要改进的地方.

[1] Jermey P M,Renshaw R J.Precipitation representation over a two-year period in regional reanalysis[J].Q J R Meteorol Soc,2016,142(696):1300-1310.

[2] Huang Y J,Cui X P,Li X F.A three-dimensional WRF-based precipitation equation and its application in the analysis of roles of surface evaporation in a torrential rainfall event[J].Atmospheric Research,2016,169(123):54-64.

[3] Balana B B,Vinten A,Slee B.A review on costeffectiveness analysis of agri-environmental measures related to the EU WFD:Key issues,methods,and applications[J].Ecological Economics,2011,70(6):1021-1031.

[4] Ross I,Misson L,Rambal S,et al.How do more extreme rainfall regimes affect ecosystem fluxes in seasonally water-limited Northern Hemisphere temperate shrublands and forests?[J].Biogeosciences Discussions,2011,8:9813-9845.

[5] Dubus L.Monthly and seasonal forecasts in the French powersector [C].In ECMWF SeminarProceedings:Seasonal Predictions,ECMWF:Reading,UK,2012:131-142.

[6] Qiu X X,Zhang F Q.Prediction and predictability of a catastrophic local extreme precipitation event through cloud-resolving ensemble analysis and forecasting with Doppler radar observations [J].Science China Earth Sciences,2016,59(3):518-532.

[7]陈凯,王立松.一种新的加权最近邻算法的降水预报试验[J].计算机仿真,2014,31(6):325-328.

[8] 刘还珠,赵声荣,陆志善,等.国家气象中心气象要素的客观预报-MOS系统[J].应用气象学报,2004,15(2):181-191.

[9] 邵明轩,刘还珠,窦以文.用非参数估计技术预报风的研究[J].应用气象学报,2006,17:125-128.

[10] 翟宇梅,赵瑞星.概率天气预报的K近邻非参数估计仿真模型[J].系统仿真学报,2005,17(4):786-788.

[11] 闵晶晶,孙景荣,刘还珠,等.一种改进的BP算法及在降水预报中的应用[J].应用气象学报,2010,21(1):55-62.

[12] 范严,程琳.实现准确预报的降水预报模型构建方法研究[J].计算机仿真,2013,30(2):351-363.

[13] 邓小花,魏立新,黄焕卿,等.运用支持向量机方法对数值模拟结果的初步释用[J].海洋预报,2015,32(2):14-23.

[14] CoverT M,HartP E.Nearestneighborpattern classification[J].IEEE Trans Inform Theory,1967,13:21-27.

[15] Song Y,Huang J,Zha H,et al.IKNN:Informative KNearest Neighbor Pattern Classification[C].Knowledge Discovery in Databases:PKDD,2007:248--264.

[16] 曾晓青,邵明轩,王式功,等.基于交叉验证技术的KNN方法在降水预报中的试验 [J].应用气象学报,2008,19(4):471-478.

[17] Mitani Y,Hamamoto Y.A local mean-based nonparametric classifier[J].Pattern Recognition Letters,2006,27(10):1151-1159.

[18] Zeng Y,Yang Y,Zhao L.Pseudo Nearest Neighbor Rule forPattern Classification [J].ExpertSystems with Applications,2009,36(2):3587-3595.

[19] Gou J,Zhan Y,Rao Y,et al.Improved pseudo nearest neighbor classification[J].Knowledge-Based Systems,2014,70(C):361-375.

[20] 吴洪兴,彭宇,彭喜元.适用于不平衡样本数据处理的支持向量机方法[J].电子学报,2006,34(12A):2395-2398.

[21] 杜娟,刘志刚,衣治安.一种适用于不均衡数据集分类的KNN算法 [J].科学技术与工程,2011,11(12):2680-2685.

[22] 刘赛艳,黄强,王义民,等.基于统计降尺度和CMIP5模式的泾河流域气候要素模拟与预估[J].农业工程学报,2015,31(23):138-144.

[23] 韩越.基于TOPMODEL模型的泾河流域水资源演变规律研究[D].西安:西安理工大学,2014.

[24] MCLOYMC.Severe storm forecast results from the PROFS 1983 forecast experiment[J].Bull Amer Mteoro Soc,1986,63:155-164.

Application of Local Mean-based Pseudo Nearest Neighbor Algorithm in Precipitation Forecast

LIN Runsheng,HUANG Mingming*
(Beijing Meteorological Information Center,Beijing 100089,China)

After analyzing daily precipitation data in Beijing city,the number of heavy rainfall events or torrential rainfall events,as compared to the number of other events such as no rain events,light rain events and moderate rain events,is significantly few.Therefore,the precipitation data of precipitation forecast in Beijing city is imbalance.In the case of the precipitation data with an uneven distribution,the forecast performance of the traditional k-nearest neighbor algorithm based precipitation forecast method will degrade dramatically due to the classification error rate of the k-nearest neighbor algorithm rising greatly.To overcome the problem which is the sample size of the precipitation forecast in Beijing city is not balanced,the precipitation forecast model is established using Local Mean-based Pseudo Nearest Neighbor(LMPNN)algorithm.Using the observed precipitation data in Beijing as the class and factors of the National Centers for Environmental Prediction-National Center for Atmospheric Research reanalysis dataset as the feature of the sample,we firstly calculated the local mean-based pseudo nearest neighbor of the sample in each class and then obtained the class label of the sample by the LMPNN rule.The extensive experiments of 24 hour precipitation forecast of Beijing city from June 1st to August 31st in 2010 were conducted.The proposed approach could get more accuracy,threat score,summary alarm rate,false alarm rate and missing alarm rate than that of the precipitation forecast method based on k-nearest neighbor algorithm.The comprehensively experimental results suggest that the proposed approach is effective.

local mean-based pseudo nearest neighbor algorithm;k-nearest neighbor algorithm;precipitation

P456.1

A

1002-0799(2017)05-0001-08

林润生,黄明明.局部均值伪最近邻算法在降水预报中的应用[J].沙漠与绿洲气象,2017,11(5):1-8.

10.12057/j.issn.1002-0799.2017.05.001

2017-02-23;

2017-03-09

预报预测核心业务发展专项quot;基于云计算环境的气象数据环境应用试验quot;(CMAHX20160701)资助.

林润生(1962-),男,高级工程师,主要研究方向为气象信息技术研究和开发.

黄明明(1986-),女,博士,主要研究方向为机器学习、模式识别.E-mail:mmhuang1205@163.com