基于改进遗传算法的孔群数控加工路径优化*
2017-11-30龚玉玲武美萍徐晓栋
龚玉玲,武美萍,徐晓栋,龚 非
(1.泰州学院 船舶与机电工程学院,江苏 泰州 225300;2.江南大学 机械工程学院 江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122;3.中国航天科工集团8511研究所,南京 210007)
基于改进遗传算法的孔群数控加工路径优化*
龚玉玲1,武美萍2,徐晓栋1,龚 非3
(1.泰州学院 船舶与机电工程学院,江苏 泰州 225300;2.江南大学 机械工程学院 江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122;3.中国航天科工集团8511研究所,南京 210007)
针对孔群加工路径优化中遗传算法存在的局部最优和收敛速度慢等问题,提出采用模拟退火算法改进遗传算法进行路径优化。首先根据孔群数控加工的特点建立数学模型,采用遗传算法设计种群编码,建立适应度函数选择优秀种群,并对保留的优秀种群进行交叉、变异等操作,实现种群进化,其次引入模拟退火算法对其适应度函数进行拉伸处理,调整种群进化差异性而加速寻优进度,同时采用改进的Metropolis准则调整接受概率,调节旧种群和新种群的进化程度,增强遗传算法的全局搜索能力。实例表明:改进算法用于某模具的孔群加工,有效克服遗传算法的早熟现象,缩短收敛次数,平均路径缩短比例达6.9%,提高了加工效率,效果良好。
孔群加工;改进遗传算法;模拟退火算法;Metropolis准则
0 引言
在孔群的数控加工中,孔群加工路径的优化设计,有利于缩短刀具空行程距离,提高加工效率和设备的使用率[1-2],因此孔群路径的优化问题成为目前CAM中研究热点问题[3-4]。目前,在解决工程实际问题时,通常采用插入法[5]、单元划分法[6]等方法,但随着孔群加工数量和规模日益增大,此类方法计算误差较大。随着近年来计算机技术的不断发展,许多学者将智能算法,如启发式算法[7]、蚁群算法和相邻排序算法[8]、遗传算法(genetic algorithm,GA)[9]等算法用于解决路径优化问题,取得了一定效果。
遗传算法借签生物进化“优胜劣汰”的遗传机制,求解简单,并行计算能力强,鲁棒性强等优点,被广泛地用于较多领域[10],在孔群的路径优化方面取得了成功的案例[11-12],如文献[11]重点研究遗传算法中参数影响,以寻找合适的参数进一步缩短孔群加工路径,但是仍存在迭代慢,甚至迭代难于收敛等问题,文献[12]采用编码、交叉和变异等方案,解决迭代中无法收敛等问题,提高优化效率,但是遗传算法优化过程中存在容易陷入局部最优。针对遗传算法中容易出现局部最优和收敛速度慢等问题,本文通过对遗传算法中适应度函数与接受概率进行模拟退火处理,实现改进遗传算法对孔群路径优化处理,获得全局最优解并提高收敛效率。
1 孔群数控加工路径模型
孔群数控加工路径优化问题与典型旅行商问题有相似的地方,即为保证数控刀具遍历每个待加工孔,寻找刀具加工的最短路径;但是也有较大区别,待加工的孔一般需要多种刀具、加工多道工序完成一个孔的加工:如钻孔、扩孔、铰孔、镗孔等工序,加工过程中需要换刀,对刀等操作,根据孔群加工的特点,建立孔群加工模型。设孔群加工模型集合表达式为:
G=(V,E,D)
(1)
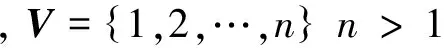
F(x)=f(x)+βd(x)
(2)
式中,f(x)为刀具孔间的行程路径长度,
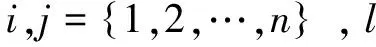

β为加权系数,取β=1.5;
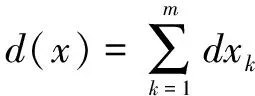
在寻找满足式(2)最优解的前提下,还需要满足工艺的加工规律:①先粗加工在精加工;②先光孔加工后螺纹加工等机加工要求。
F(x)为全局孔群加工路径总长度,优化目标是寻找一条最优的路径,使得F(x*)=min{F(x)}。
2 改进遗传算法的加工路径优化
遗传算法是通过种群编码和种群选择、交叉、变异等操作,生成新后代,在新后代中选择优秀后代作为下一代的种群进行循环操作,留下最优子代作为最优解。
2.1 种群编码
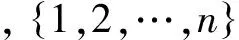
2.2 种群适应度函数
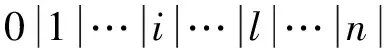
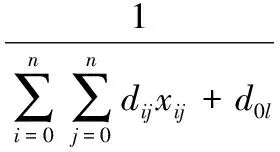
(i≠j)
(3)
适应度函数为遍历所有孔且回到初始机床参考点的距离倒数。优化目标是选择适应度大的染色体,适应度越大,路径越短,染色体质量越好,反之染色体质量越差。
2.3 种群选择、交叉、变异操作
(1)种群的选择操作
根据进化论理论,由式(3)计算的染色体适应度,选择适应度强的染色体,删除差的染色体,根据选中的染色体概率作为其适应度占种群里适应度总和的比例,根据比例选择一定百分比的优秀个体进行下面的交叉、变异操作,以保证全局性的优化选择[13]。
(2)种群的交叉操作
对保留的染色体,采用映射杂交方式,确定交叉操作父代,将父代样本两两分成一组,随机选择任意位置按照概率px交叉操作。交叉后,如果同个个体染色体之间出现重复基因,利用部分映射的方法消除重复基因。假定在[1 10]范围随机选择整数r1和r2,确定两个位置,对两个位置中间数据进行交叉操作。假设r1=3,r2=6,则:
位置:1 2 3 4 5 6 7 8 9 10


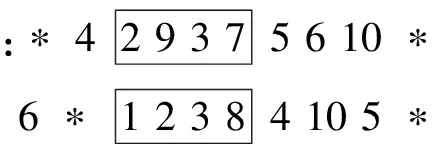
交叉操作后,不重复的数字保留,重复的数字暂时以*代替,并利用中间段对应关系进行映射,消除冲突,结果为:
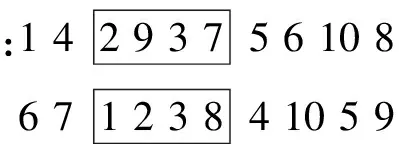
(3)种群的变异操作
随机选择任意位置按照概率pm变异操作,变异后,产生新染色体。如在[1 10]范围内随机挑选整数r1和r2,确定两个位置,假设r1=3,r2=6,则:
位置: 1 2 3 4 5 6 7 8 9 10
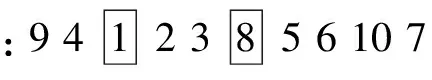
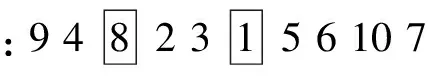
2.4 改进遗传算法的种群进化
文献[11]采用的遗传算法,通过种群的编码、选择、交叉和变异方案,实现了种群的优化,但是计算中随机性较大,对进化程度控制不足,首先,在进化初期,一些个体会因竞争力很强而控制优化过程,容易陷入局部最优而无法获得全局最优解;其次,在进化后期,由于个体的适应度差异慢慢变小,选择机制可能趋于随机任意选择,进化缓慢,难以搜索到全局最优解。因此引入模拟退火算法,种群进化中,不仅接受优秀种群,而且还以一定概率接收恶化解,从而增强种群的多样性,使搜索方向回退,跳出局部最优陷阱,以寻找全局最优解;同时通过模拟固体退火过程(升温过程、平衡过程、冷却过程三个阶段)的温度控制,对适应度函数进行退火拉伸处理,以提高全局收敛速度。
(1)适应度函数退火处理
令初始最高温度Tmax,最低温度为Tmin,降温函数采用衰减函数:
Tk+1=αTk(k=0,1,2,…)
(4)
式中,α为降温系数,该值为常数,取0.5~0.99,该值决定了降温速度。衰减量少时迭代次数增加,从而搜索更大的解空间,返回更好的解。每个温度下对应的循环次数为gmax,当循环次数为g。
通过温度调整,适应度函数在温度Tmax高时(遗传算法初期),温度降低较快,计算的各个染色体的适应度函数差别比较小,染色体被复制的概率也低,避免个别好的染色体充斥全部种群,造成早熟;而随后温度以α倍率缓慢降低,目标函数相近的染色体适应度函数值差异将不断增大,优秀染色体优势更加明显,防止种群进化停滞不前。通过对适应度函数的拉伸处理,可以解决遗传算法的早熟和进化停滞等缺陷,提高寻优速度。
(2) 接受概率退火处理
若路径长度函数为f(d),当前解的路径为f(d1),新解的路径为f(d2),路径差为df=f(d2)-f(d1),采用Metropolis准则修改种群规则为:
(5)
①当df<0时,表示新解路径比当前路径短,则保存该新个体,即f(dcurrent)=f(d2);
②当df>0时,表示新解路径比当前路径长,则按照概率P1对新个体随机与其它子染色体位置对换后保存,计算df,当df<0则保存,否则还原成原种群。
③当df=0时,按照概率P2对新个体随机与其它子染色体位置对换后保存,计算df,当df<0则保存,否则还原成原种群。
2.5 改进遗传算法的实现
改进遗传算法需要从大量路径中寻找一条满足式(2)的最优路径,流程见图1所示,其具体步骤如下:
Step1:设置算法参数:即设置种群规模s,初始温度Tmax,终止温度Tmin,降温系数α,交叉概率px,变异概率pm,内循环次数gmax,最优染色体pbest;
Step2:设置当前温度t=Tmax;
以上案例表明伊匹单抗和曲美木单抗无论是单药还是联合PD-1/PD-L1通路的单克隆抗体帕博利珠单抗和纳武利尤单抗,均获得了较好疗效,联合治疗具有更高的抗瘤效果。但是均出现了少数心脏不良反应,如心肌缺血、心肌纤维化、心律失常、免疫性心肌炎、心肌病及心力衰竭症状,可能与免疫相关性心肌细胞保护缺失有关,CTLA-4在维持包括心肌在内的不同组织起保护性作用,上述小鼠实验及临床案例充分证实使用CTLA-4单克隆抗体抑制CTLA-4基因表达,心肌细胞不能得到有效保护,进而出现心肌细胞不同程度的缺血和坏死,而自身免疫性心肌炎及心衰可危及生命。
Step4:设置当前循环次数g=1;
Step5:根据种群的适应度选择策略,选择优秀染色体种群p;
Step6:对选择的染色体种群p,按照交叉概率px,变异概率pm操作生成新种群p′;
Step7:对于新种群p′,利用Metropolis准则,选择是否替换当前种群p;
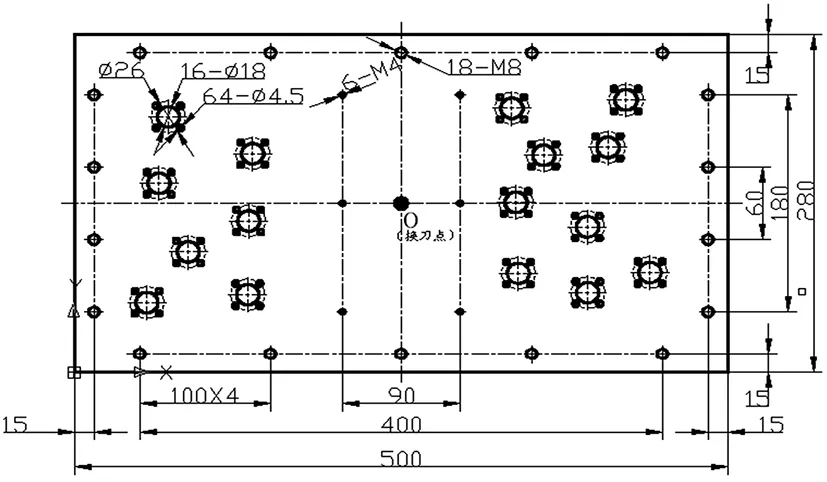
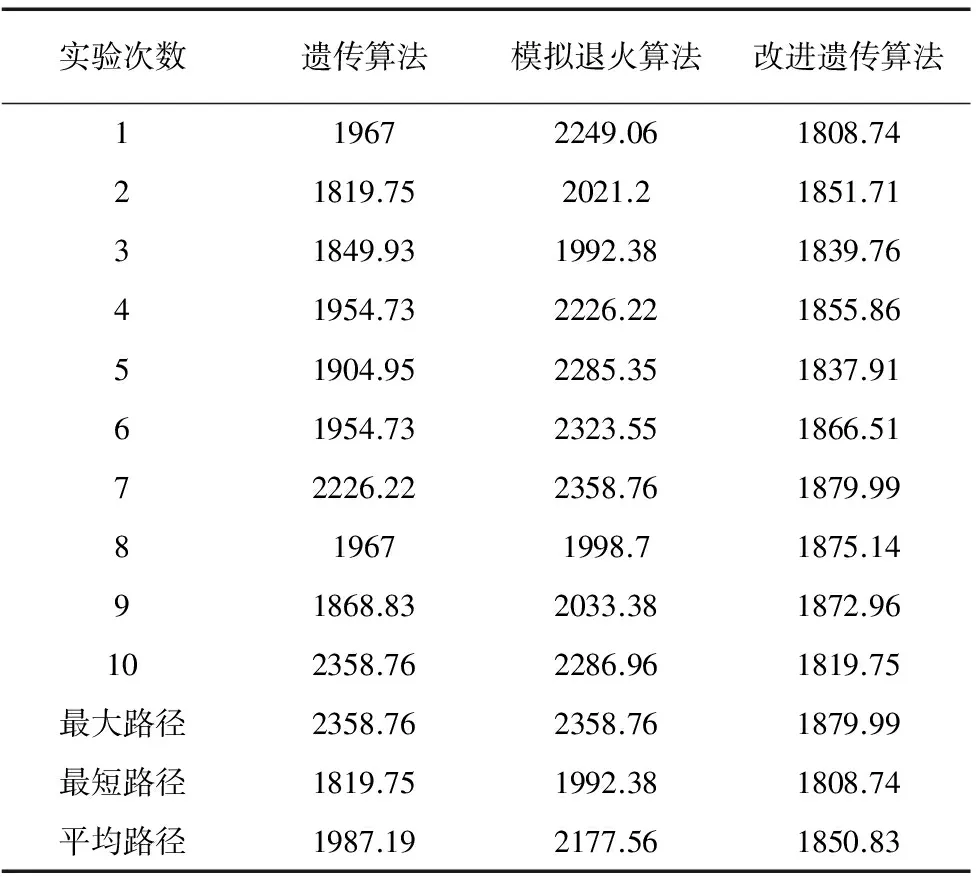
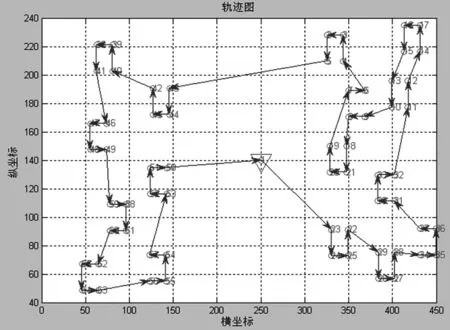
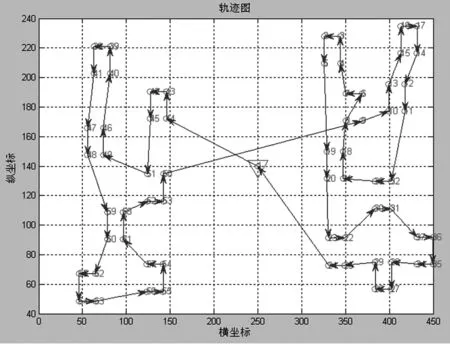
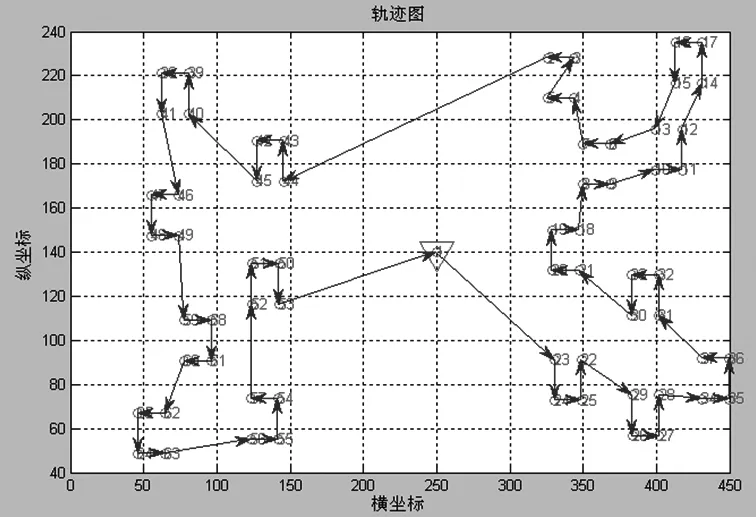
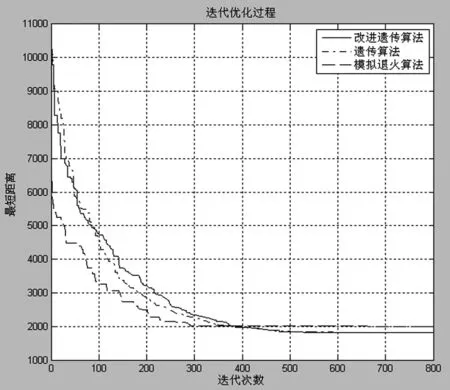
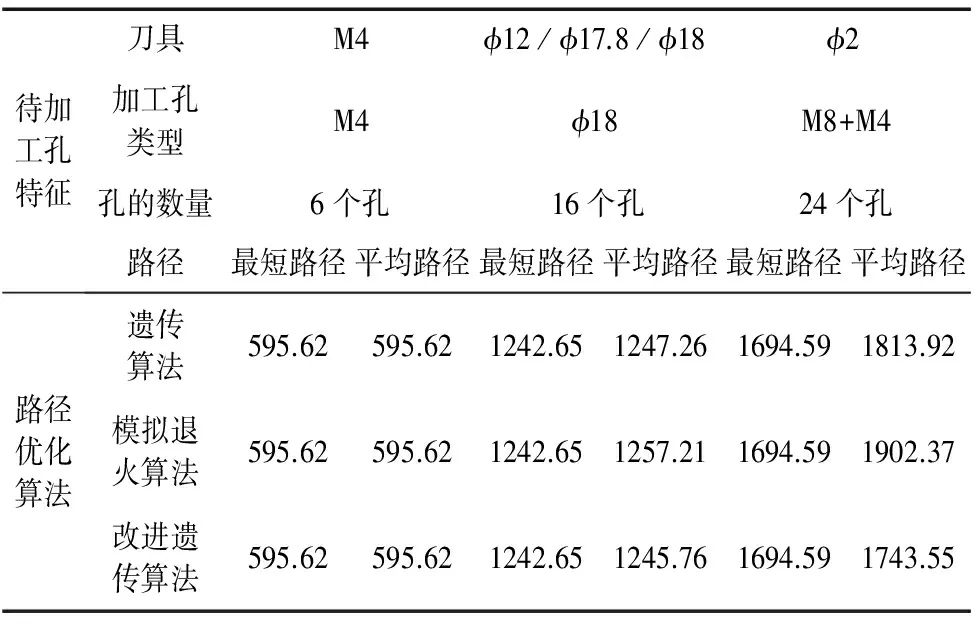
Step8:令g=g+1,如果g Step9:令t=αT,如果t>Tmin,转入Step4;否则转入Step10; Step10:输出最优解pbest及最短路径f(dbest)。 图1 改进遗传算法的孔群路径优化流程图 本文以某模具孔群加工为例,见图2所示,孔的特征及加工方式见表1所示。 图2 某模具孔群加工布置图 孔特征尺寸数量钻刀1钻刀2钻刀3攻丝1攻丝2铰刀1键槽刀1立铣刀1立铣刀2a1M818ϕ2ϕ6M8a2M46ϕ2M4a3ϕ4.564ϕ4.3ϕ4.5a4ϕ1816ϕ12ϕ17.8ϕ18 由图2和表1可见,该板有4类待加工孔,尺寸分别为M8、M4、φ4.5、φ18,对应的孔的数量分别为18、6、64、16个。首先采用中心钻孔定位,然后用不同直径钻刀钻孔,最后攻丝、开键槽或铰孔等加工。其中M8与M4均需要钻刀1φ2加工,加工时为减少换刀次数可以同时加工。具体的加工工序为中心孔钻刀1φ2→钻刀2φ6→攻丝1M8→攻丝2M4→钻刀3φ4.3→铰刀1φ4.5→键槽刀1φ12→立铣刀1φ17.8→立铣刀2φ18 。刀具均在0处完成换刀,完成各道工序加工。 改进遗传算法的参数设置为:初始种群规模s=100,初始温度Tmax=100℃,终止温度Tmin=0℃,降温系数α=0.99,各温度下的最大迭代次数gmax=200,交叉概率px=0.7,变异概率pm=0.01。 为验证改进遗传算法的优化效果,选择与遗传算法[12],模拟退火算法[14]分别进行路径优化比较。以铰刀1φ4.5(64个孔)的刀具加工路径为例,分别进行10次优化实验,优化结果见表2所示。 表2 优化实验路径长度 由表2中10次路径优化结果可见,改进遗传算法在最大路径,最短路径和平均路径都优于前两种算法,其中平均路径缩短比例分别为6.9%和17.7%,10次路径优化中最短路径见图3所示,最短路径优化迭代搜索过程图见图4所示。 图3中三种算法的最短路径分别为1819.75,1992.38,1808.74,改进遗传算法相比遗传算法、模拟退火算法,其路径缩短了11.01,183.64。 由图4分别为改进遗传算法、遗传算法、模拟退火算法最短路径的迭代次数,其迭代次数分别为:551,591,663次,搜索迭代次数减少了40次,112次,可见改进遗传算法以较快的速度获得全局较优解。 (a)遗传算法最短路径图 (b)模拟退火算法最短路径图 (c)改进遗传算法最短路径图图3 三种算法钻孔最短路径图 图4 三种算法最短路径迭代搜索过程图 对图2中其它几种特征孔进行路径优化,重复做10次实验,统计路径长度见表3所示。 表3 各种孔的优化实验路径长度 由表2和表3可见,加工6个规则孔时,三种算法计算结果一样,但是随着孔群的数量从6个增加到64个孔,相比传统遗传算法,平均路径缩短0.1%(16个孔),4.0%(24个孔),6.9%(64个孔);相比模拟退火算法,平均路径缩短0.9%(16个孔),9.1%(24个孔),17.7%(64个孔),由此可见孔的数量越多,排列不规律时,该算法的优势越明显。 本文采用改进遗传算法解决孔群加工路径优化问题。通过对遗传算法中种群选择、交叉、变异等操作,并在种群进化过程中引入模拟退火算法的Metropolis准则,调节新旧种群的更新,有效改进了传统遗传算法早熟、局部搜索能力不强等缺陷,特别是针对数量多、排列不规则的孔群加工,优化程度更加明显。 [1] ONWUBOLU G C,CLERC M. Optimal path for automated drilling operations by a new heuristic approach using particle swarm optimization[J]. International Journal of Production Research,2004,42(3):473-491. [2] HSIEH Y C,LEE Y C,YOU P S. Using an effective immune based evolutionary approach for the optimal operation sequence of hole-making with multiple tools[J]. Journal of Computational Information Systems,2011,77(2):411-418. [3] Luong L, Spedding T. An integrated system for process planning and cost estimation in hole making[J]. International Journal of Advanced Manufacturing Technology,1995,10(6):411-415. [4] 陈琳,刘晓琳,潘海鸿,等. 孔群分类加工路径的优化算法[J]. 制造业自动化,2013,35(17):46-49. [5] 童行行,王凌,何京芮. 旅行商问题基于参考点的相邻插入法及其改进[J]. 计算机工程与应用,2002(20): 63-65. [6] 赵玉成,袁树清,许庆余. TSP问题的单元划分法[J]. 力学与实践,1998,20(6):35-36. [7] 曾议,孙莉,孙友文,等. 启发式算法的孔群加工路线模糊多目标优化[J]. 现代制造工程. 2016(4):44-50. [8] 潘海鸿,刘晓琳,廖小平,等.钣金激光切割加工CAD/CAM软件的孔群加工路径优化算法[J].组合机床与自动化加工技术,2013(11):110-113. [9] 李国闻,张丹,杜海遥,等. 基于遗传算法的机电产品布线结构优化设计方法[J].中国科技论文,2015, 10 (16):1944-1948. [10] Li S, Liu Y, Li Y,et al. Process planning optimization for parallel drilling of blind holes using a two phase genetic algorithm[J]. Journal of Intelligent Manufacturing , 2013, 24(4):791-804. [11] 许兆美,金卫凤,李健.基于遗传算法的孔群加工路径优化[J]. 机械设计与制造,2011(2):31-33. [12] 肖军民.一种改进遗传算法在孔群加工路径中的优化[J].组合机床与自动化加工技术,2015(2):151-153. [13] Li YH,Guo H,Wang L,et al. A hybrid genetic-simulated annealing algorithm for the location-inventory-routing problem considering returns under E-supply chain environment[J]. Scientific World Journal, 2013(11):1653-1656. [14] 裴小兵,贾定芳. 基于模拟退火算法的城市物流多目标配送车辆路径优化研究[J]. 数学的实践与认识,2016,46(2):105-113. ResearchonPathOptimizationofHoleGroupMachiningBasedonImprovedGeneticAlgorithm GONG Yu-ling1,WU Mei-ping2,XU Xiao-dong1,GONG Fei3 (1.School of Shipbuilding & Electromechanical Engineering,Taizhou University, Taizhou Jiangsu 225300, China; 2.Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment & Technology, School of Mechanical Engineering, Jiangnan University, Wuxi Jiangsu 214122, China) Aiming at the problems of local optimum and slow convergence of genetic algorithm in the optimization of hole group machining path, an improved genetic algorithm based on simulated annealing algorithm is proposed. Firstly, mathematical model is established according to the characteristics of hole group machining, then the encode model of the population is designed based on genetic algorithm, the operations of crossover and mutation of outstanding population retention are implemented by the fitness function to make the population evolve. Secondly, the genetic algorithm is combined with simulated annealing algorithm to draw the fitness function for adjusting the evolution of population differences and accelerating the optimization progress, at the same time the improved Metropolis standards are used to adjust the probability of acceptance and evolution degree of the old and new regulation of population for enhancing the global search ability of genetic algorithm. Examples show that the algorithm has been used in hole group machining of the mould. The improved genetic algorithm compared with traditional genetic algorithm can overcome the prematurity of traditional genetic algorithm effectively, reduce the number of convergence and reduce by more than 6.9% on average path, which has increased of efficiency and has good effect. hole group machining; improved genetic algorithm; simulated annealing algorithm; Metropolis criterion 1001-2265(2017)11-0052-05 10.13462/j.cnki.mmtamt.2017.11.014 2017-01-07; 2017-02-20 2016年度泰州学院校级科研课题(TZXY2016YBKT002);泰州学院双语教学课程建设项目(泰院教发[2016]11号) 龚玉玲(1978—),女,湖北襄阳人,泰州学院讲师,硕士,研究方向为船舶与机电工程技术,精密加工和检测的教学与研究,(E-mail)79043638@qq.com。 TH166;TG659 A (编辑李秀敏)
3 实例分析
3.1 孔群加工特点

3.2 路径优化实验及数据分析
3.3 实验数据分析
4 结论
