紧水滩水电站厂内经济运行分析
2017-11-29刘国富楼其禄陈海荣
刘国富,楼其禄,陈海荣
(国网浙江省电力公司紧水滩水力发电厂,浙江 丽水 323000)
紧水滩水电站厂内经济运行分析
刘国富,楼其禄,陈海荣
(国网浙江省电力公司紧水滩水力发电厂,浙江 丽水 323000)
通过分析紧水滩水电站机组特性曲线,应用动态规划法提出各机组最优运行组合,实现机组安全高效运行,达到节能降耗的目的。
水电站;动态规划法;经济运行
0 引言
水电站机组的经济运行主要是充分发挥其性能,最大限度地利用水资源,创造出一系列的综合经济效益。水电站经济运行的任务是在负荷一定的情况下,以耗水最小为优化准则;或在水量一定的条件下,以发电量最大为优化准则,寻求机组最优台数组合和机组间负荷最优分配。水电站经济运行是水电厂调度的重要内容,它不仅是电力系统安全、可靠、优质运行的基础,而且是提高电力系统经济效益的重要措施之一[1]。水电站经济运行主要通过厂内经济运行、短期经济运行和长期经济运行进行实施。而厂内经济运行即实时调度,主要任务是将每个小时分配到的负荷分配到各个机组,并根据负荷因素的实时变化,调整各机组出力配置,实现实时控制,保证水轮机组在高效区运行。
1 动态规划法
动态规划法作为运筹学的一个分支,是一种用以求解决策过程最优化的数学方法。美国数学家贝尔曼等人在研究多阶段决策过程的优化问题时,提出了非常著名的最优化原理。他们把多阶段过程转化为一串单阶段问题,再利用各阶段之间的关系,逐个进行求解,由此便创立了解决这类过程优化问题的新方法一动态规划法。
在解决多阶段决策问题中,各个阶段釆取的决策一般来说是与时间有关的,决策即依赖于当前状态,又引起状态的变化转移,一个决策序列就是在不断变化的状态中产生出来的,故有“动态”的含义,而这种方法被称为动态规划方法。在面对水轮机组最优配置的选择问题时,正是一种多阶段决策问题。
寻找水电站水轮机组最优化组合方案,所要找寻到的决策对象为,每一台水轮机组,在满足给定条件下,所分配到的负荷量,以实现最大发电量或者最小耗水量。水电站经济运行的机组负荷分配问题,实质上是空间最优化问题,装机n台机组的电站,其机组间负荷分配构成了n阶段决策问题。固定机组编号,每台机组就可视为一个阶段,如果各阶段决策即机组出力是最优的,那么由这些决策所构成的策略即为最优策略,也就是我们说的电站最优运行方式。这样便使得寻求水电站厂内经济运行方案的问题变成了一个多决策过程的最优化问题。可以按如下思路把水电站厂内经济运行问题化为动态规划问题。
阶段的确定:假设我们的水电站有n台机组,则我们将动态规划递推过程分为n个阶段,每个阶段由i表示,i=1,2,3,…,n;每个阶段有i台机组出力。
状态变量:第i阶段由i台机组所发出的有功负荷,用Pi表示;
决策变量:第i阶段,第i台机组出力Ni;
状态转移方程:

目标函数为:
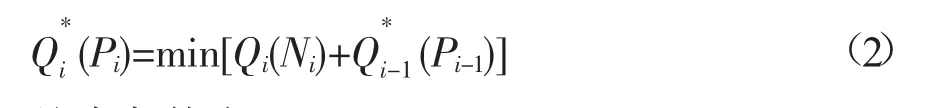
约束条件为:

式中:——第i-1阶段,i-1台机组出力为Pi-1时的流量最优值;
Qimin、Qimax——第i台机组允许流量的上下限;
Nimin、Nimax——第i台机组允许出力的上下限;
N——该时段所有机组规定的出力总和。
2 电站概况
紧水滩水电站是浙江省瓯江流域大溪上的一座梯级电站,是浙江省电力系统主力调峰水电厂,电站以220 kV和110 kV电压接入浙江电网,主要担负浙江省电力系统调峰、调频、调相、进相及事故备用等任务,为浙江电网的安全供电发挥了重要作用,并且在电网AGC自动发电运行中担当主力。紧水滩水电站总装机容量300 MW(6台×50 MW),水轮机型号为HL220-LJ-300,发电机型号为SF-K50-30/6400,机组先后于1987-1988年投产[2]。
由于紧水滩HL220-LJ-300水轮机存在着双水力振动区这一设计缺陷,使其高效运行范围受到限制,而随着自动发电控制系统投运后,又加剧了机组振动,严重威胁电站安全稳定运行。为此,紧水滩电站经过前期调研、试验、专家论证以及报批,并取得有关部门的批准,启动紧水滩水电站机组增容改造工程,对机组转轮进行换型改造,以解决水轮机组稳定性问题,并提高机组额定出力10%,分别对1号、2号、5号、6号机组进行改造,增容改造内容包括转轮更换、导水机构部件更换、接力器更换、发电机定子铁心更换、定子线棒更换及相关配套电气设备更换等。
3 水轮机数学模型建立
紧水滩电站总装机容量为300 MW,有三种不同水轮机型号共6台机组,具体参数如表1:
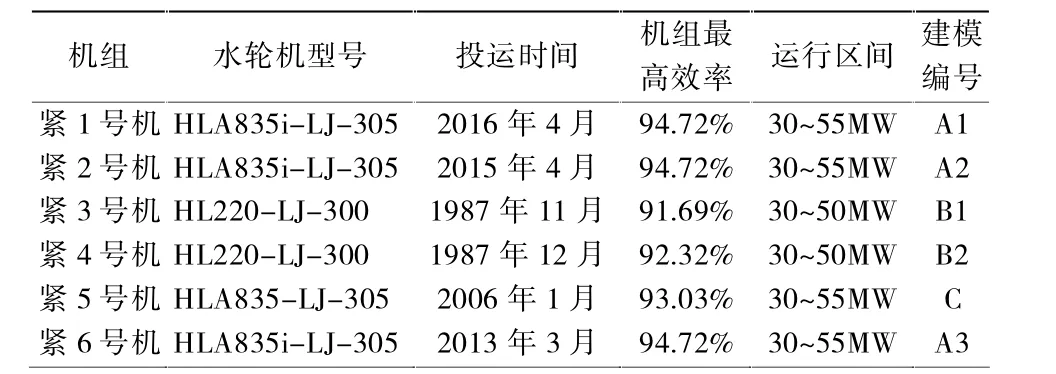
表1紧水滩电站水轮机信息
(1)首先需要得到由水轮机厂家提供的转特性曲线(H-P)和(H-Q)。
(2)在(Hmin,Hmax)区间内将运转特性曲线的 H轴分为若干等份,每一个点做一条平行于P轴的直线。
(3)该直线与等效率线 η=f(P,H)有若干个交点,摘录对应的效率、出力、水头数据。
(4)利用N=9.81ηQH公式,计算对应的机组流量。
(5)将该直线与等效率线的每一个交点上的Q值都计算出来,便得到在该水头下,出力P与流量Q的离散数学关系Q=Q(P)。
(6)用最小二乘法,选幂函数为拟合基函数,对离散关系进行拟合,得到该水头下的流量特性函数,即 Q=Qc(Pc)。
(7)用同样的方法对另外两类水轮机进行拟合,得到水电站的水轮机组的综合数学模型,即:
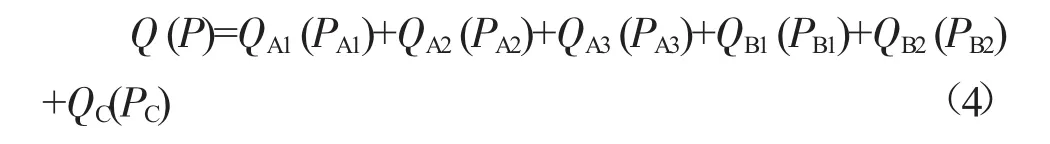
其中:
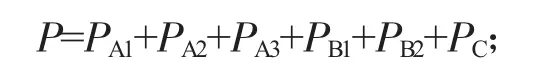
Q(P)为在满足总出力情况下的总耗水量。
利用编程语言建立6台水轮机的数学模型函数。要求在满足给定P的前提下,合理分配PA1、PA2、PA3、PB1、PB2、PC的值,以使得 Q(P)最小,达到经济性最高的目的。
通过各水轮机特性曲线分析,在同一水头下,紧水滩2、6号机耗水量最小,效率最高,1号机次之,5号机再次之,3、4号机耗水量最大。因此,从效率最优条件考虑,机组发电时应先开2、6号机,再开1号机、5号机,最后开3、4号机。
4 动态规划法应用
4.1 动态规划法计算
紧水滩电站共有6台水轮机,则选择为六个阶段。
以A1为第一阶段,计算在其出力范围(30~55MW)内各个点的最优值;以A1与A2共同出力为第二阶段,计算在其出力范围(30~110MW)内各个点的最优值;以A1、A2与A3同时出力为第三阶段,计算在其出力范围(30~165 MW)内各个点的最优值:以此类推,计算至第六阶段各个点最优值,各出力条件下机组最优出力分配见表2。
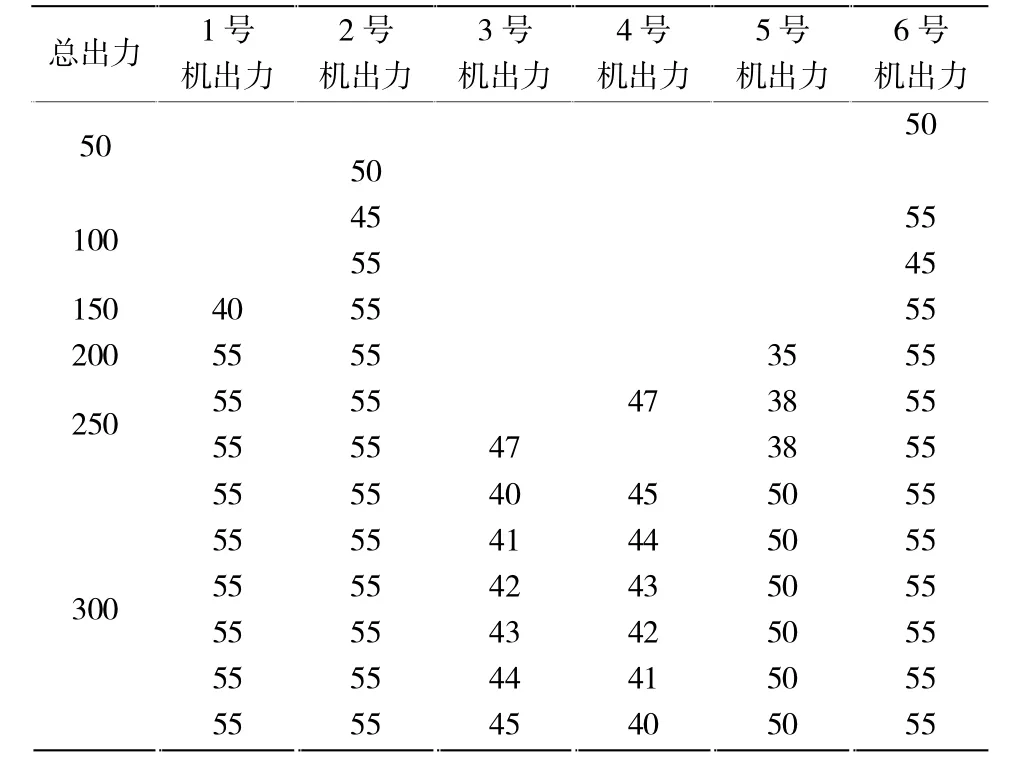
表2各出力条件下机组最优出力分配 单位:MW
从表2的优化计算结果看出,符合水轮机特性曲线分析结论,即先开启2、6号发电机组,再开1号和5号机组,最后才开3、4号发电机组。
4.2 优化组合结果
当N=100 MW,水位为180 m时,优化组合结果见表3:N=100 MW优化配置结果。

表3 N=100MW优化配置结果
当N=300 MW,水位为180 m时,优化组合结果见表4:N=300 MW优化配置结果。

表4 N=300MW优化配置结果
4.3 优化效益分析
根据水电站的发电运行方案及各发电机组实际出力安排,计算实际发电流量。按该原则下的流量损耗如表5水电站实际发电出力安排所示:
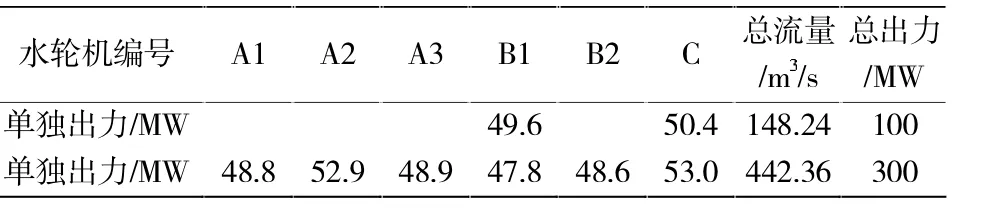
表5水电站实际发电出力安排
通过使用优化百分数进行分析:

其中:
Qc表示水电站常用方案耗水量;
Qt表示优化后方案耗水量;
OPT越大,表示方案越好,经济性越强。
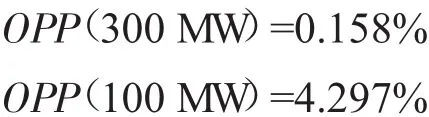
5 结语
通过对电站水轮机特性曲线分析和动态规划法应用,提出机组开机组合及开机次序,并对机组发电出力进行优化分配,提高水电站的经济效益,特别在机组未满负荷运行情况下,合理安排高效率机组在高效发电区间运行,电站发电效益提高明显。当水电站发电机组较多,且需要更精确分析时,该方法可能出现维数灾,应尽量避免[3]。
[1]胡军富.乌溪江水电厂经济运行分析[J].小水电,2011,160(4):149-151.
[2]浙江省瓯江紧水滩水电站运行设计报告[R].电力工业部华东勘测设计研究院,1980.
[3]向凌,周建中,杨敬涛.一种消除动态规划法中维数灾的新方法[J].电力系统及其自动化学报,2004(6):76-78.
F407
A
1672-5387(2017)11-0056-03
10.13599/j.cnki.11-5130.2017.11.021
2017-08-25
刘国富(1977-),男,高级工程师,从事水电站水库调度及水调自动化管理。
