基于在线增量LSSVM的污水软测量模型

周文君，李明河

（安徽工业大学 电气与信息工程学院，安徽 马鞍山 243002）

基于在线增量LSSVM的污水软测量模型

周文君，李明河

（安徽工业大学 电气与信息工程学院，安徽 马鞍山 243002）

出水COD浓度的精准预测是污水处理期望实现的目标，然而现有的离线模型对大规模时变更新的水质数据，预测效果会逐渐变差.针对该情况，采用离线模型结合增量学习的思想，提出基于在线增量LSSVM污水软测量模型，即首先建立基于LSSVM污水软测量模型，然后针对不断更新的增量样本，通过误差阈值进行筛选，有选择地增量学习，并结合合适的剪枝操作，实现样本长度的固定，对出水COD浓度在线预测.仿真结果表明：相较于标准LSSVM模型，本模型在预测精度、预测时间上，都具备不同程度的优势，很好地解决了离线学习的问题，实现在线精准预测.

污水软测量；在线增量LSSVM；出水COD浓度；误差阈值；剪枝操作

随着工业现代化的不断发展,环境污染特别是工业污水问题尤为突出.污水处理是一个具有强非线性、时变性、大滞后等特点的复杂工业过程,重要水质出水COD浓度的检测以及预判都显得非常困难,因此软测量技术作为传统检测技术的延伸和发展,应用于污水处理具有重要的现实意义.

支持向量机(support vector machine,SVM)由于其良好的非线性系统辨识能力,近年来在污水处理中取得了广泛应用［1-3］.然而其中大部分都是属于离线模型的范畴,一旦遭遇数据大规模时变更新时,模型的离线学习方式将不能够满足实际需求,预测效果逐渐降低.因此,很多专家学者提出离线模型结合增量学习的思想［4-10］,使模型可以随着时间更新变化具备不断调整的能力.由于大多数增量式算法都是基于传统支持向量机,即在线求解凸二次规划问题,计算效率较低,运算时间较长.为了提高运算效率,本文引入最小二乘支持向量机(LSSVM),用线性方程组取代二次规划运算,建立基于在线增量LSSVM学习算法,并添加筛选机制和剪枝操作,使模型相较于标准LSSVM模型,在准确性和在线性都有一定的改善和提高.

1 改进的在线增量LSSVM

1.1 在线增量学习

最小二乘支持向量机通过引入非线性变换ϕ:Rn➝Rm,把样本数据从低维输入空间映射到高维特征空间,在高维特征空间中构造线性回归函数.增量学习中,样本数据随着时间不断添加,也就是样本集随着时刻t每次产生一个增量样本.设更新后的样本集表示为｛(xt,yt)｝,其中,x(t)＝［x1,x2,…xt］,y(t)＝［y1,y2,…yt］,x(t)∈Rn,y(t)∈R.

LSSVM回归函数表示为:

令U(t)＝H(t)-1＝(Qt＋C-1I)-1,得到:

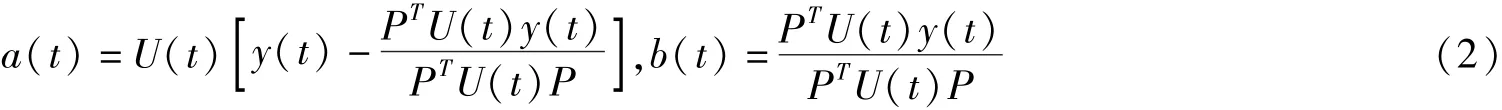
由式(2)可知,对矩阵U(t)的求解,本文选择矩阵迭代的方式求逆运算.

当t＋1时,添加新增样本,相应H(t)则变成(t＋1)*(t＋1)的方阵:

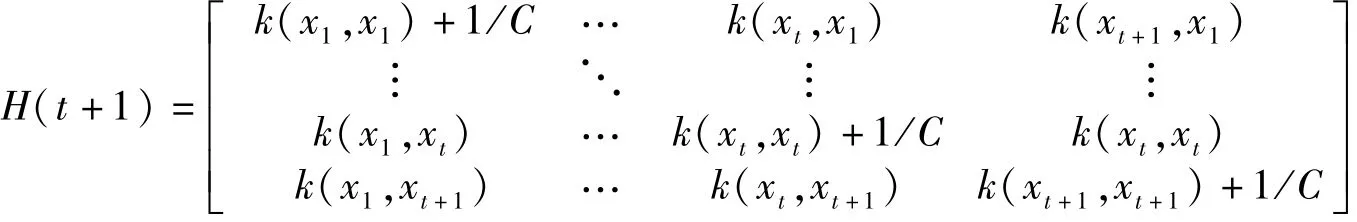
矩阵分块可得

式(3)是U(t＋1)和U(t)之间的一个递推公式,可知当添加增量样本时,新矩阵求解可以根据以前存储结果进行迭代求解,避开对大维度矩阵求解,缩短了运算时间,提高了运算效率,给大规模数据在线预测提供了可行性.

1.2 改进措施

1.2.1 误差阈值

污水处理数据是时变更新的,当大规模参数数据无差别地当作增量样本进行学习时,模型的负担将会加重,效率将会下降,所以一定的筛选机制实现有选择学习,在保证准确度的前提下减少学习次数,提高学习效率［11］.本文以模型训练结果为参照,所选取样本训练偏差的平均值作为误差阈值ek,即其中,n是所选训练样本的个数,yi是实际值,是预测值.

该方法的思想是针对每个样本进行样本增量之前,首先由预测模型进行预测,求偏差,当预测偏差超过误差阈值,才对样本进行增量学习,而对于没有超过的样本,则认为该类样本对LSSVM模型的效果影响不大,没有多余其它信息的产生,不对其进行增量学习.

1.2.2 剪枝操作

当模型面临庞大的预测集数据时,计算机储存的历史结果不断增多,矩阵维度也相继增大,对应的迭代运算也将会变得更加复杂,所以增量学习的同时需要添加必要的剪枝操作,本文参照文献［11］的剪枝操作,认为时变模型中原始数据包含的信息最弱,选择剪掉最早加入的样本数据.

假设当前模型已经学习l个样本,然后选择去除最早的样本,此时迭代矩阵可以表示为:

图1 在线增量LSSVM算法流程

其中,v＝k(x1,x1)＋1／C,V＝［k(x1,x2)…k(x2,x1)］.

由式(4)可知可以通过剪枝进行迭代求解.改进算法的流程如图1所示.

2 模型仿真

本文基于对BAF污水处理出水COD的预测研究,实验数据来源于某环保公司BAF项目正常运作下各仪表现场检测,并通过PLC传输,在上位机显示的实时采样值.采样系统定时在线采集与出水COD有着密切联系的变量,即进水COD浓度、进水NH3-N、溶解氧(DO)浓度、进水PH、水力停留时间(HRT)、TN(总氮)、TP(总磷)等.为了保证建模的准确和便利,通过主元分析法选取部分过程变量取代之前的所有变量,并反映之前变量的所有信息,即通过SPSS软件利用贡献率大小对出水COD浓度影响因子进行筛选,最终选取进水COD浓度、进水NH3-N、溶解氧(DO)浓度、进水PH作为模型的输入变量,建立出水COD浓度的污水软测量模型.

2.1 预测精度

为了验证本文改进算法在精度上的有效性,筛选出其中的200组污水数据,其中150组作为训练数据,且当作滑动窗口的大小,后50组作为在线预测数据.核函数选用RBF核函数,并且选用PSO算法进行参数优化,用本文改进的在线增量LSSVM算法进行训练预测,仿真曲线如图2和图3所示.

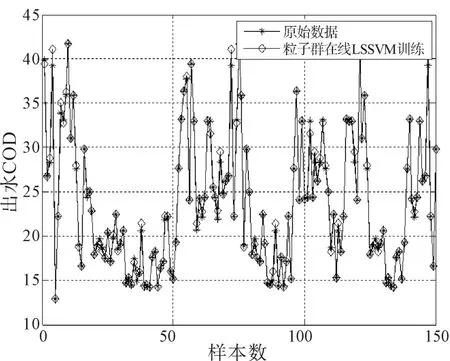
图2 在线增量LSSVM模型训练曲线

图3 在线增量LSSVM模型测试曲线

由图2和图3可以看出,在线算法的模型准确度较高,当模型遭遇大规模时变数据时,可以实现对出水COD浓度在线准确预测.为了更直观地验证在线模型的准确性,从选择数据的角度进行分析,以均方根误差作为模型优劣的评判依据,公式为.选择在线增量LSSVM、增量LSSVM和标准LSSVM三种模型分别进行建模,并且记录各自的均方根误差,结果如表1所示.

由表1可知,相比于标准的LSSVM模型,增量LSSVM模型均方根根误差为0.4979 mg/L,略有提升,即增量学习解决了离线模型面临的问题,但对于计算精度的提升并没有很好效果.在线增量LSSVM模型均方根误差为0.3442mg/L,相较于以上两者,预测精度得到一定幅度的提升.由此可见,在线算法可以避免离线学习的弊端,实现对出水COD浓度的准确预测.

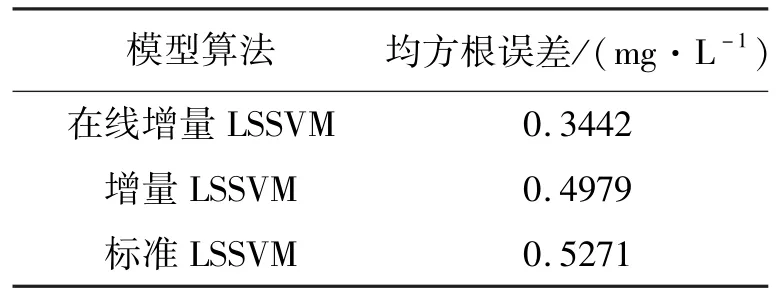
表1 不同预测模型均方根误差对比

表2 在线增量LSSVM和标准LSSVM运算时间对比

2.2 预测时间

增量学习主要通过矩阵迭代代替复杂的求逆运算,缩短了运算时间,提高了效率.本文选择标准LSSVM和在线增量LSSVM,分别记录面对不同数量样本情况下模型运算时间,结果如表2所示.

由表2可知,无论样本个数是多少,在线增量LSSVM模型的运算时间都比标准LSSVM要短,且随着样本数量的增多,在线模型时间的增量幅度比标准LSSVM要低很多,对处理数量规模庞大样本的优势就更明显,提高运算效率.

3 结论

本文以LSSVM为模型算法,结合增量思想,将增量学习算法应用于出水COD浓度的预测,很好地解决了离线模型面临大规模数据时预测效果变差的弊端,在保证预测准确度的前提下,实现了在线测量.并且,本文也添加相应的改进措施,即误差阈值的设置以及剪枝操作对模型进行进一步的完善,是模型的稀疏性和在线性得到一定的改进和完善,更好的实现对出水COD浓度的在线精准预测.

［1］ 尹先清,罗晓明,王文斌,等.基于SVM方法的含聚污水电化学处理过程控制研究［J］.西安石油大学学报:自然科学版,2016(3):92-97.

［2］ 程 呈.混合多模型曝气生物滤池污水处理软测量建模研究［D］.马鞍山:安徽工业大学,2016.

［3］ 连晓峰,李晓婷,潘 峰.机理模型与补偿模型相结合的污水处理工艺出水指标软测量预测模型研究［J］.计算机与应用化学,2013(10):1143-1147.

［4］ 潘世超.增量支持向量机学习算法研究［D］.太原:山西大学,2015.

［5］ 陈沅涛,徐蔚鸿,吴佳英.一种增量向量支持向量机学习算法［J］.南京理工大学学报,2012(5):873-878.

［6］ 王 玲,穆志纯,郭 辉.一种基于聚类的支持向量机增量学习算法［J］.北京科技大学学报,2007(8):855-858.

［7］ GU B,SHENG V S,WANG Z,et al.Incremental learning for v-support vector regression［J］.Neural Networks,2015,67:140-150.

［8］ LIANG Z,LI Y F.Incremental support vector machine learning in the primal and applications［J］.Neurocomputing,2009,72(10):2249-2258.

［9］ CAUWENBERGHS G,POGGIO T A.Incremental and decremental support vector machine learning［C］ //NIPS.the 13th International Conference on Neural Information Processing Systems.Cambridge:MIT Press,2000:388-394.

［10］ LIU X,ZHANG G,ZHAN Y,et al.An incremental feature learning algorithm based on least square support vector machine［C］//International Workshop on Frontiers in Algorithmics.Changsha:Springer Berlin Heidelberg,2008:330-338.

［11］ 梅 倩.LS-SVM在时间序列预测中的理论与应用研究［D］.重庆:重庆大学,2013.

［12］ 刘双印,徐龙琴,李振波,等.基于PCA-MCAFA-LSSVM的养殖水质pH值预测模型［J］.农业机械学报,2014(5):239-246.

［13］ 杨 柳,孙金华,冯仲科,等.基于PSO-LSSVM的森林地上生物量估测模型［J］.农业机械学报,2016(8):273-279.

［14］ 张浩然,汪晓东.回归最小二乘支持向量机的增量和在线式学习算法［J］.计算机学报,2006,29(3):400-406.

［15］ 苏书惠,张绍德,谭敬辉.基于支持向量机的污水处理软测量算法的研究［J］.自动化与仪器仪表,2009(6):6-9.

Wastewater Soft Sensor Modeling Based on Online Incremental LSSVM

ZHOU Wenjun，LI Minghe
（School of Electrical and Information Engineering， Anhui University of Technology， Maanshan 243002， China）

Precise prediction of COD concentration is the desired target in the wastewater treatment process.How⁃ever,the existing off-line soft-sensing model’s predictive effect will be gradually worse facing large-scale real-time updated water quality data.Aiming at this,it proposed a wastewater soft sensor model based on on-line in⁃cremental least squares support vector machine(LSSVM)was proposed in this paper.Firstly,a wastewater soft sensor model based on on-line incremental LSSVM was built up；secondly,the error threshold was set to achieve a selective incremental learning and constantly update support vectors；thirdly,the matching pruning operation was selected to achieve the size of the sample fixed.The simulation results demonstrated that the model can solve the problems of off-line learning,and can realize online precise forecasting.

wastewater soft-sensing；on-line incremental LSSVM；effluent COD concentration；error threshold value；pruning operation

X703；TP301.6

A

2095-4476（2017）11-0005-04

2017-08-02

安徽省软科学研究计划项目(1502052034)

周文君(1992—),女,安徽无为人,安徽工业大学电气与信息工程学院硕士研究生.

(责任编辑:饶 超)