基于高度函数的旋转机械轴心轨迹识别方法
2017-11-29孙国栋艾成汉汤汉兵
孙国栋,艾成汉,周 振,汤汉兵
(湖北工业大学机械工程学院,湖北 武汉 430068)
基于高度函数的旋转机械轴心轨迹识别方法
孙国栋,艾成汉,周 振,汤汉兵
(湖北工业大学机械工程学院,湖北 武汉 430068)
针对旋转机械轴心轨迹的识别准确率低、识别速度慢等问题,结合BP神经网络,提出基于高度函数的旋转机械轴心轨迹识别算法。该算法首先利用小波滤波对旋转机械不同故障的轴心轨迹进行预处理,其次采用高度函数描述子提取预处理后的轴心轨迹图像特征,然后使用部分图像的特征训练BP神经网络,最后将训练好的BP神经网络用于剩余图像的识别。实验结果表明:在自建的模拟轴心轨迹数据库中,该算法识别率最高,达94.2%,单个样本识别耗时0.006ms,满足实时性要求;对于实际测量的转子不平衡故障检测准确率也达91.6%,有较高的实用价值。
高度函数;BP神经网络;轴心轨迹;特征提取;故障诊断
0 引 言
旋转机械随处可见,小至洗衣机等家用电器,大到水电机组、离心压缩机等大型设备,与人们的生活息息相关。这些设备一旦发生故障,会造成大量的时间和经济损失,甚至有可能危及人们的生命安全。因此,旋转机械的故障诊断显得尤为重要。对旋转机械而言,其转子的运动状态包含了大量的故障信息,可以通过分析转子的轴心轨迹来诊断旋转机械可能出现的故障[1]。
目前,对于轴心轨迹的识别,国内外学者相继提出了不同的方法。陈坚等[2]使用Hu不变矩作为特征向量,采用BP网络进行特征训练,以实现轴心轨迹的自动分类。万书亭等[3]在Hu不变矩的基础上,将其改进为不变线矩,但由于不变矩自身特性,对于复杂图形的检测率还有待提高。付波等[4]提出了基于改进傅里叶描述子的轴心轨迹识别方法,并证明了其可行性,但傅里叶变换无法将频谱的相位信息充分使用[1],且算法复杂度高,严重影响了识别算法的实时性。Wang等[5]使用链码作为特征对轴心轨迹进行识别,陈晓玥等[6]使用一种模拟人眼的方法对轴心轨迹进行识别。然而,这些方法都难以准确表述轴心轨迹的特征,迫切需要一种新的有效方法对轴心轨迹进行识别。
王军伟等[7]提出基于高度函数(height function,HF)的特征描述子,采用传统动态规划(dynamic programming,DP)寻找形状间的最佳对应关系,并在MPEG-7等多种形状匹配数据库上进行了测试,实验结果表明HF含有丰富的形状特征,能有效表征形状的轮廓特征。虽然并行DP算法[8]能有效提升形状匹配的效率,对于含有1400张图像的MPEG-7数据库,识别1张图像仍需4.23s,难以满足轴心轨迹识别的实时性需求。并由于BP神经网络在特征分类中优秀的表现,因此使用BP神经网络来对提取后的特征进行分类。
1 基于高度函数的轴心轨迹识别算法
1.1 高度函数
高度函数,来源于视觉曲率理论,是一种使用“高度”这一物理特征来描述图像轮廓信息的方式,这里的“高度”指轮廓上某一点的切线到另外一点的距离。基本原理如图1所示。
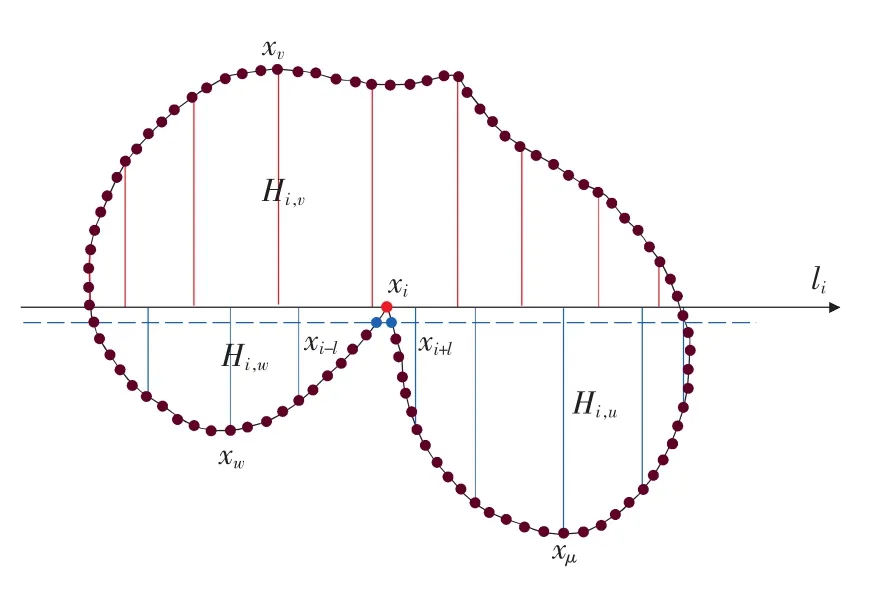
图1 高度函数基本原理示意图
对于图中所示轮廓,平均选取轮廓上的N个采样点,设点集为 X={xi}(i=1,2,3,…,N)。规定逆时针为正方向,则每一点xi的高度函数Hi即为过该点处的切线到剩余点距离的有序序列,如下式所示:

式中Hi,j代表过点xi处轮廓的切线到点xj的距离,但由于并非每一个轮廓点都存在切线,因此使用最邻近的两点xi-1与xi+1的连线代替过该点的切线。轴心轨迹轮廓的高度函数则为逆时针方向所有点X的高度函数的集合,因此该轮廓的高度函数描述子为一个(N-3)·N 维矩阵。
高度函数的优点在于其丰富的局部特征,具有平移、旋转、缩放不变性[7],并且计算方便,易于实现。尽管如此,高度函数也有其自身的局限性:包含数据量大,计算用时长。文献[7-8]使用动态规划(DP)算法来进行分类,DP算法需要大量的时间来进行样本HF描述子的比对计算,耗时长、效率低,难以满足算法实时性要求。为此,需要寻求一种更加合理的方式,来对轴心轨迹的高度函数进行分类。
1.2 基于高度函数和BP神经网络的轴心轨迹识别方法
BP神经网络即反向传播算法,是一种按误差逆向传播的前馈神经网络,在机器学习中应用十分广泛,其基本结构包括输入层、隐藏层和输出层3个部分,本文所用BP网络结构如图2所示。BP神经网络的训练过程包括正向传播和反向传播两种过程,先由输入层开始正向传播,将输入信息传递给隐含层,再经过输出层得到结果;若结果与实际结果不符,则进入反向传播过程,采用梯度下降方式修正隐含层的权值。在输入层输入HF描述子;隐藏节点通过经验试凑的方法[9]选取15个隐藏节点,激励函数使用S型logsig函数;输出层节点数与要识别的种类对应,这里选5,输出层激励函数为线性函数purelin。

图2 BP神经网络基本结构

图3 算法流程图
根据高度函数和BP神经网络,所设计算法的主要流程如图3所示。首先分别对轴心轨迹训练集和测试集提取轮廓,然后在所得轮廓上选取N个采样点,根据采样点计算高度函数描述子,对于每个轴心轨迹样本图得到一个 (N-3)·N维的特征矩阵;最后使用训练样本的特征矩阵训练BP神经网络,并对测试样本的特征矩阵进行测试,得到识别结果。
2 实验与结果分析
实验环境如下:Windows 10(×64)操作系统,Inter Corei7的处理器和8GB内存,编程软件为Matlab2015b。
在上述环境下,先模拟出轴心轨迹数据库,然后采用本文算法HF+BP对轴心轨迹进行训练与识别,并以Hu不变矩和形状上下文分别替代HF与本文方法进行对比实验,同时对BP算法和DP算法的优劣进行了实验验证。
2.1 轴心轨迹模拟
使用Matlab软件,按照下式对轴心轨迹进行模拟[10]:

式中:A1、A2、B1、B2——x、y的一、二倍频分量;
ω——角速度;
α、β——x、y的初始位置相位。
各种故障对应图形如表1[10]所示。

表1 故障对应轴心轨迹图形
由于实际轴心轨迹常常含有噪声,向模拟的轨迹中加入信噪比为25dB的高斯噪声。对于含有噪声的轴心轨迹,常采用小波滤波[10]对轴心轨迹进行提纯,提纯效果如图4所示。从图中可以看出,小波滤波的提纯效果良好。

图4 小波滤波前后
对所有模拟的图像都进行小波滤波,得到滤波后的各类图像共计1000张,每类200张,其中100张图像用来训练,剩余100张用来测试。模拟出的部分图像见图5和图6。

图5 部分训练所用轴心轨迹

图6 部分测试所用轴心轨迹
2.2 轴心轨迹识别实验
在模拟得到训练图像和测试图像之后,使用图3所述流程对轴心轨迹进行训练和识别。选取HF采样点60个,计算得到1 000个57×60的特征矩阵。再将Matlab工具箱中的BP神经网络周期设置为1 000,目标误差设置为0.000 1,隐藏层节点个数为15个,设置完成后再使用训练样本的HF特征训练该网络,训练过程如图7所示。为了便于实验对比,以下所有BP神经网络参数设置均与此处一致。
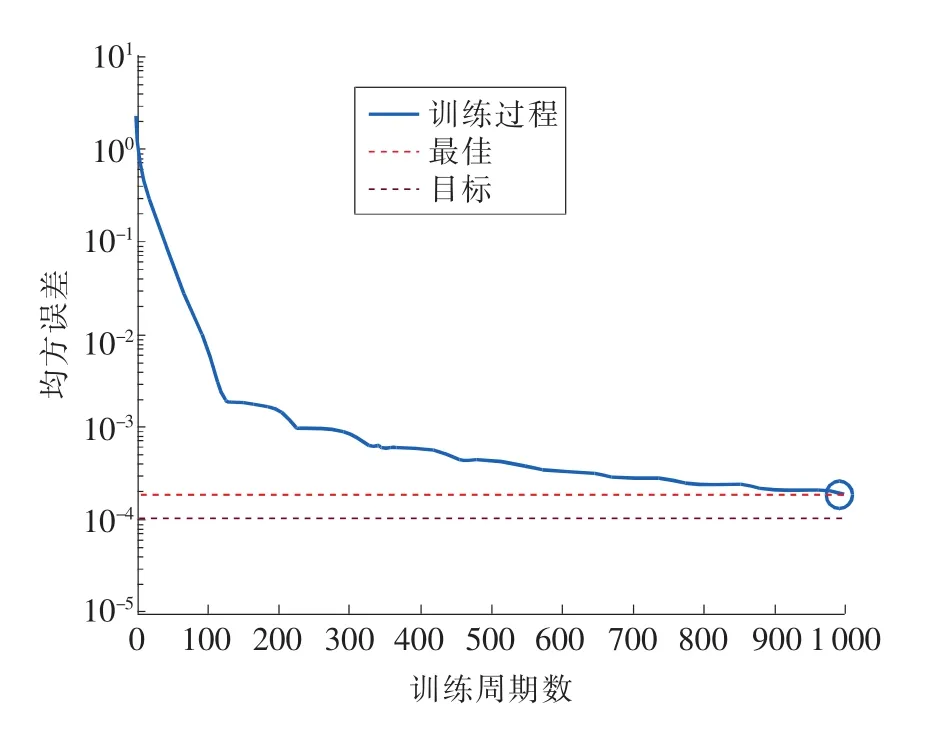
图7 HF+BP训练过程
由图可知,HF+BP训练过程中,前100周期均方误差收敛速度较快,300周期以前还有一定的波动,300~1000周期除偶尔小波动外呈稳定下降趋势,到1000周期已经基本收敛,均方误差达0.00018。训练完成后统计10次测试样本准确率均值,最终结果如表2所示。

表2 实验结果
使用Hu不变矩[11]进行的对比实验过程见图8。如图所示:Hu+BP训练周期达到120后均方误差变化已基本不大,在0.1以下,收敛较快,1000周期后均方误差为0.349,已基本收敛完成,但误差远远大于HF+BP训练同样周期后的误差0.00018。可见Hu对图形的分类描述远远不及HF精细,到一定程度以后已无法对图像进一步分类。
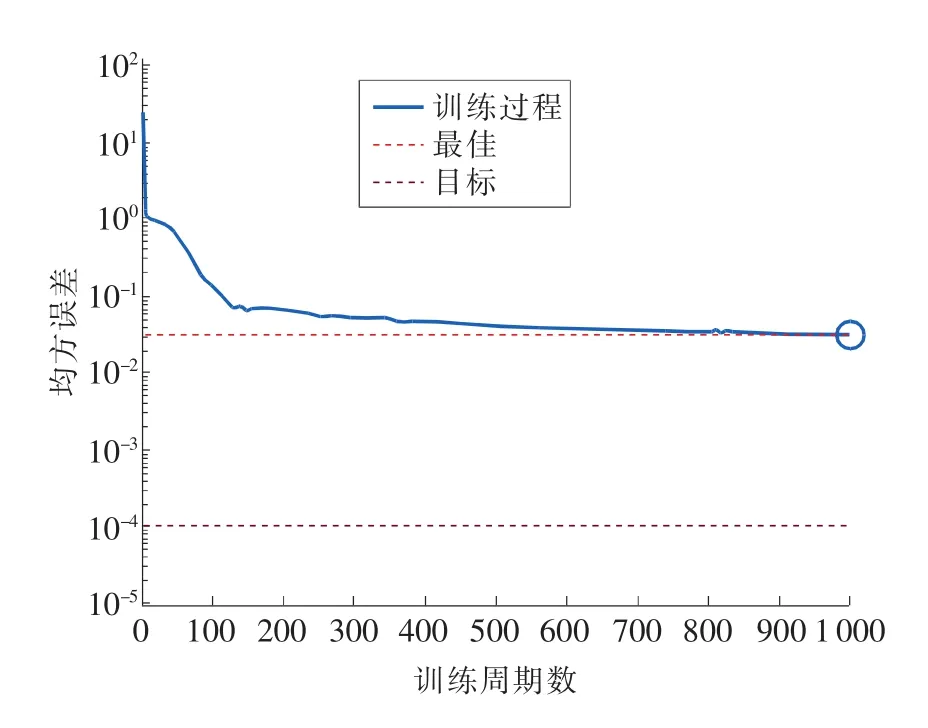
图8 Hu+BP训练过程
为了进一步验证高度函数的优越性,使用另一种经典的轮廓特征提取方法——形状上下文[12](shape context)对轴心轨迹进行特征提取。形状上下文的特征点选取和高度函数一致,为60,并使用相同的BP神经网络识别。
此外,为了对比BP神经网络与动态规划算法效果,使用DP算法对高度函数与形状上下文特征分别进行识别。在使用DP算法的过程中,针对自建数据库采用如下评价方式:对于每一个检测样本,使用动态规划算法进行匹配相似度排序后,在最相似的前10个样本中统计,认为种类数目最多的那一类即为该检测样本的检测结果。
2.3 实验结果分析
由表2可知:同样使用BP神经网络进行训练的3种特征描述子中,Hu不变矩对轴心轨迹特征的描述有一定的效果,其优点在于描述简单,仅用7个不变矩就能表达一定的轨迹信息,单个样本检测时间仅为0.002 ms,实时性好,但识别准确率低;相较而言,SC+BP算法比Hu+BP准确率略有提升;而HF+BP实验准确率比Hu+BP高出14.5个百分点,比SC+BP高出9.8个百分点,准确率大大提升,检测时间虽然所增加,但仅为0.006ms,在实时性要求的范围内。
SC+BP与SC+DP相比,检测时间少了6个数量级,实时性更好,但准确率却下降了2.2%,实验过程中还发现SC+BP多次实验的结果波动范围大,不能满足算法稳定性的要求。说明SC对轴心轨迹的刻画不够深刻,包含大量的干扰信息,导致学习算法的不稳定。
HF+DP算法对轴心轨迹的检测有较高的准确率,但缺点是检测时间过长。将HF与BP神经网络相结合,不仅准确率更高,提升2.4个百分点,且检测时间减少了7个数量级,实时性更好。
2.4 实际应用
为了验证该算法的实用性,将其应用于实际轴心轨迹故障检测。但由于实验条件限制,仅通过滚动轴承转子试验台添加配重螺母的方式模拟出转子不平衡一类故障,该故障对应于椭圆形的轴心轨迹。图9为转子及配重螺母,图10为测得的不平衡轴心轨迹及其经过预处理后的图像。

图9 实验所用转子及配重螺母

图10 实测轴心轨迹及其预处理
通过螺母数目和位置的不同,模拟多种不平衡轴心轨迹图像。选取320幅包含多种不同配重的不平衡轴心轨迹图像,使用前文中使用模拟数据的高度函数所训练的BP神经网络对实际图像进行检测。检测准确率为91.6%。
可见该算法对于轴心轨迹有较强的识别能力,若采用实际测量的不同故障图像的高度函数带入BP神经网络训练,检测结果预计还能进一步提高。
3 结束语
由于传统轴心轨迹识别中特征提取效果不佳,提出基于高度函数描述子与BP神经网络的轴心轨迹图像识别方法,实验结果表明高度函数描述子对轴心轨迹的描述效果优于Hu不变矩和形状上下文描述子,BP神经网络较动态规划算法具有更大的实时性优势,准确率也有一定提升。所提出的轴心轨迹识别方法在模拟实验中识别率高达94.2%,在实际轴心轨迹的试验中也达到91.6%,识别速度快,一个样本识别仅需0.006ms。该算法亦对其他需要识别轮廓和线条的场合有一定的启发作用。后期将搭建更优的转子试验台,对各种不同故障进行实际测量、识别;并针对高度函数本身进行改进研究,通过参考点的选取优化高度函数描述子。
[1]孙慧芳,潘罗平,张飞,等.旋转机械轴心轨迹识别方法综述[J].中国水利水电科学研究院学报,2014,12(1):86-92.
[2]陈坚,叶渊杰,陈抒,等.基于不变矩和神经网络的泵机组轴心轨迹自动识别 [J].排灌机械工程学报,2011,29(1):67-71.
[3]万书亭,吴炳胜.基于改进型不变线矩特征的机组轴心轨迹形状自动识别[J].热能动力工程,2008,23(2):144-147.
[4]付波,周建中,陈文清,等.一种基于傅里叶描述子的轴心轨迹自动识别方法 [J].电力系统自动化,2004,28(12):40-44.
[5]WANG C, ZHOU J, KOU P, et al.Identification of shaft orbit for hydraulic generator unit using chain code and probability neural network [J]. Applied Soft Computing,2012,12(1):423-429.
[6]陈晓玥,周建中,肖剑,等.一种模仿人眼的汽轮机轴心轨迹识别方法[J].振动、测试与诊断,2015,35(4):677-684.
[7]WANG JW, BAIX, YOU X E, etal.Shape matching and classification using height functions[J].Pattern Recognition Letters (PRL),2012,33 (2):134-143.
[8]孙国栋,张杨,李萍,等.用于快速形状匹配的精确型高度函数特征描述[J].光学精密工程,2017,25(1):224-235.
[9]肖锦成,欧维新,符海月.基于BP神经网络与ETM+遥感数据的盐城滨海自然湿地覆被分类[J].生态学报,2013,33(23):7496-7504.
[10]周训强.旋转机械轴心轨迹的提纯、特征提取与自动识别研究[D].重庆:重庆大学,2010.
[11]SIVARAMAKRISHNA R, SHASHIDHARF N S.Hu’s moment invariants:how invariant are they under skew and perspective transformations[C]∥WESCANEX 97:Communications Power and Computing. Conference Proceedings IEEE, 1997:292-295.
[12]吴晓雨,何彦,杨磊,等.基于改进形状上下文特征的二值图像检索[J].光学精密工程,2015,23(1):302-309.
(编辑:刘杨)
Axis orbit identification of rotating machine based on height function
SUN Guodong, AI Chenghan, ZHOU Zhen, TANG Hanbing
(School of Mechanical Engineering,Hubei University of Technology,Wuhan 430068,China)
In order to solve the problems of low accuracy and slow speed of the identification for axis orbit of rotating machine,an algorithm based on height function and BP neural network is presented to identify the axis orbit of rotating machinery.The algorithm firstly preprocesses the axis orbit of the rotating machinery with different faults by using wavelet filter.Secondly,the preprocessed axis orbits image features are extracted by using height function descriptor.Then,a BP neural network is trained by using the features of some images.Finally,the trained BP neural network is used to identify the residual images.The result of test shows that this algorithm has the highest identification rate reaching 94.2%in the self-built simulative axis orbit database,and the time consumed by the individual sample identification is 0.006 ms,which satisfies the real-time requirement.For actual measurement,the accuracy of identifying the image of rotor unbalanced fault is 91.6%,which shows a high practical value.
height function; BP neural network; axis orbit; feature extraction; fault diagnosis
A
1674-5124(2017)09-0118-05
10.11857/j.issn.1674-5124.2017.09.021
2017-05-20;
2017-06-23
国家自然科学基金(51775177,51675166)
孙国栋(1981-),男,湖北天门市人,教授,博士,研究方向为计算机视觉、机器学习。
