基于VMD和谱峭度的滚动轴承早期故障诊断方法

唐贵基，刘尚坤

（华北电力大学机械工程系，河北 保定 071003）

基于VMD和谱峭度的滚动轴承早期故障诊断方法

唐贵基，刘尚坤

（华北电力大学机械工程系，河北 保定 071003）

针对滚动轴承故障信号为多分量非平稳振动信号、故障早期特征微弱诊断困难的问题，该文提出变分模态分解（VMD）结合谱峭度的滚动轴承早期故障诊断方法。首先对振动信号进行VMD分解得到若干分量信号，选择峭度最大分量作为最优分量，然后对最优分量进行快速谱峭度计算并进行带通滤波、凸显故障冲击成分，通过分析滤波信号包络谱中故障频率成分实现故障诊断。实验数据分析结果表明该方法能有效诊断轴承早期故障，有一定的工程应用价值。

变分模态分解；快速谱峭度；滚动轴承；早期故障诊断

0 引 言

泵、风机等旋转机械常以滚动轴承作为支撑，当轴承处于故障早期时损伤点小，产生的故障冲击成分往往比较微弱，早期故障诊断就是从复杂的传感器信号中提取出微弱的故障特征进而判断故障，对监测设备运行和避免重大事故发生有重要意义。

文献[1]利用基于双重Q因子的稀疏分解方法提取出微弱特征进行故障诊断，但该方法需要设置较多参数；文献[2]利用经验模态分解方法进行降噪并结合谱峭度滤波进行了滚动轴承早期故障诊断，然而该分解方法存在模态混叠等问题影响分析准确度[3]；文献[4]将最小熵反褶积和快速谱峭度算法（fast spectral kurtosis，FSK）相结合用于滚动轴承微弱故障提取并进行故障诊断，但最小熵反褶积的鲁棒性欠佳。

Dragomiretskiy等[5]提出了一种新的多分量信号自适应准正交分解方法——变分模态分解（VMD），该方法采用频域迭代方式搜寻变分模型最优解来确定每个分量的中心频率及带宽，通过对频域的自适应剖分实现分离各分量，在机械故障诊断中得到应用[6-8]，VMD方法能够将频率接近的谐波信号，频率突变信号进行有效分离[8]，适于多分量非平稳信号的分离。快速谱峭度计算相当于能自适应选取参数的带通滤波器，能有效抑制噪声干扰凸显故障冲击成分[9]，结合两者的优点本文提出了基于VMD和谱峭度的轴承早期故障诊断方法，即首先利用VMD对振动信号进行分解并选择峭度最大的分量作为最优分量，再用FSK对最优分量进行带通滤波处理，最后通过分析滤波信号包络谱中故障频率成分实现故障诊断。

1 变分模态分解

VMD假设多分量信号f由K个有限带宽的调幅调频分量uk组成，uk被称为本征模态函数（intrinsic mode function，IMF），uk对应的中心频率为ωk，VMD构造的约束变分模型如下：

式中：{uk}——K个IMF分量；

{ωk}——K个频率中心。

各分量的带宽确定方法如下：1）通过Hilbert变换得到uk的解析信号及其单边谱；2）通过乘以指数函数e-jωkt把估计的uk的中心频段移至基频段上；3）计算该调制信号梯度范数L2的平方，估计出各模态信号带宽。

为求解该约束变分问题，通过引入式（2）形式的增广Lagrange函数将式（1）转换为非约束变分问题：

式中：α——二次项的平衡参数；

λ——Lagrange乘子。

对式（2）采用方向交替乘子算法进行求解，从而使uk和ωk不断迭代更新，最后得到式（2）的鞍点即为模型的最优解，而频域中的各个分量由下式求解：

VMD迭代计算流程为

2）n=n+1，循环开始；

VMD算法参数主要包括平衡参数α和分量个数K，文献[10]指出较小的α值适于分析冲击故障（本文取2000），分量个数K采用文献[6]的中心频率观察法进行选取。

滚动轴承故障振动信号通常是包含故障周期性冲击成分、同时也是包含噪声和其他周期成分的多分量信号，本文经过分析发现，振动信号经VMD后，虽然能提取到故障特征频率，但最优分量中仍含有噪声等干扰成分，导致故障特征不够明显，为避免漏诊或误诊有必要再进行后续快速谱峭度计算及滤波处理。

2 谱峭度

谱峭度最初由Dwyer提出，用于在频域中度量信号的非高斯成分并确定所在的频带，Antoni等[11]进一步研究了谱峭度，用四阶谱累积量进行了定义并提出了频带滤波的快速谱峭度算法（FSK），通过计算整个频域的谱峭度，能够准确找到冲击成分所在的谱峭度最大的频带及带宽。

设 Y（t）是非平稳信号 x（t）的系统激励响应，则x（t）在频域的 Wold-Cramer分解表达式为

式中 H（t，f）为 Y（t）在频率 f处的复包络函数。

Y（t）的四阶谱累计量定义为

其中S（f）为谱瞬时矩，用作度量复包络能量，其定义为

定义谱峭度为

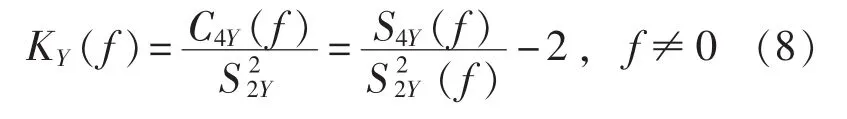
综上所述，本文提出的基于VMD和FSK的早期轴承故障诊断流程为

1）设定VMD参数对振动信号进行分解，以峭度为准则选择包含冲击成分最多的分量作为最优分量。

2）利用FSK算法对最优分量进行带通滤波处理，提取故障冲击特征。

3）对滤波后的分量信号进行包络谱分析，诊断故障。

3 实验数据分析

3.1 内圈故障分析

滚动轴承实验台及内圈故障如图1所示，用线切割在欲测试的圆柱滚子轴承NU205（内圈可拆卸）内圈加工出宽0.1mm、深0.2mm的沟槽模拟故障，振动数据用加速度传感器采集并添加高斯噪声模拟早期故障状态，采样频率为12.8kHz，分析点数6400。轴承节圆直径D=39mm，滚动体直径d=7.5mm，压力角 α=0°，滚动体个数 n=12，轴转频 fr=24 Hz，内圈故障特征频率fi=171.2Hz。

图1 滚动轴承实验台及内圈故障

图2 内圈故障振动信号的时域波形和包络谱

表1 K=4时各分量的归一化中心频率

图3 各IMF分量的时域波形

图4 分量IMF4的包络谱

内圈故障振动信号的时域波形及其包络谱如图2所示，时域波形中没有明显的规律性故障冲击，包络谱中有一定幅值的转频fr，但内圈故障频率fi的幅值不突出，难以诊断发生了内圈故障，也说明故障处于早期阶段。对该信号应用中心频率观察法进行VMD分解，当K=4时各分量的归一化中心频率如表1所示，其对应的各个IMF分量如图3所示，IMF4的峭度（4.424 5）最大，说明该分量包含了最多的冲击成分，为最优分量，其时域波形体现出周期性的冲击特点，对应的包络谱如图4所示，图中转频fr明显，故障频率fi相对也比较突出，表明VMD对分量信号的分解能力较好，但图中内圈故障特征的其他频谱结构不是很清楚且存在干扰成分，有必要进一步滤波处理。图5是分量IMF4的快速谱峭度图，图中表明最优带通滤波器中心频率为3400Hz，带宽为480Hz（椭圆标识），以该参数对最优分量IMF4进行带通滤波得到滤波信号的时域波形及其包络谱如图6所示，时域波形中规律性冲击成分明显，其包络谱中fi、2fi的内圈故障频率成分明确且该故障频率被转频fr调制现象也明显表现出来，说明进行FSK滤波的必要性，同时也表明了本文方法对早期内圈故障的良好分析效果。

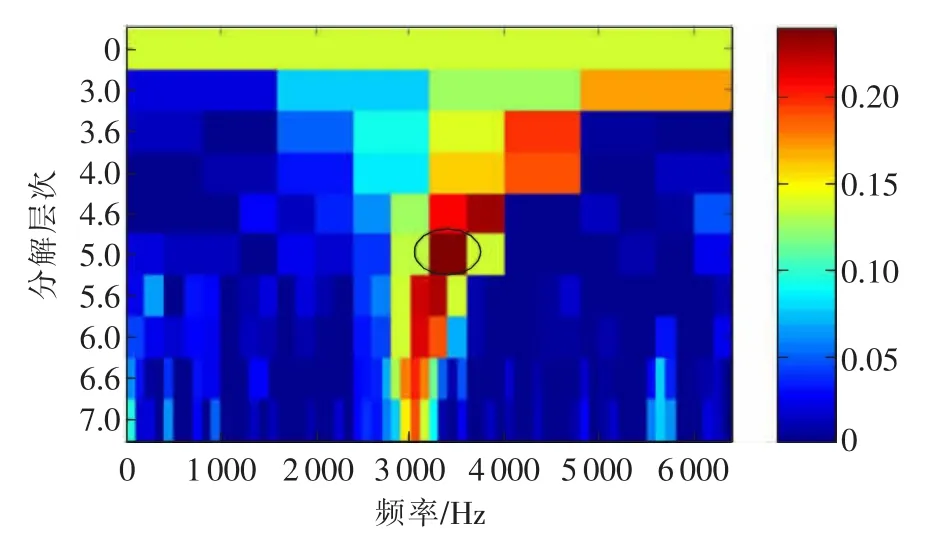
图5 分量IMF4的快速谱峭度图

图6 分量IMF4经FSK滤波后的时域波形和包络谱

为了对比，采用EMD方法对早期内圈故障信号进行分解，共得到12个分量，图7为峭度最大分量的时域波形和包络谱，时域波形中体现出了一定的周期成分，包络谱中转频fr及1倍内圈故障频率fi被解调出来，但幅值不够突出，较本文方法分析效果差。

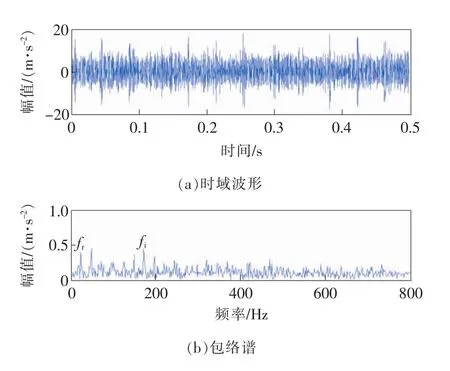
图7 峭度最大分量的时域波形和包络谱

3.2 外圈故障分析

外圈故障信号采用美国辛辛那提智能维护中心的深沟球轴承全寿命实验数据[12]，滚动轴承参数见表2，转速为2000r/min，采样频率fs=20kHz，外圈故障频率为230Hz。图8为故障轴承垂直方向传感器采集的各个实验数据均方根值XRMS的趋势图，图中7 020 min时轴承振动信号出现明显波动，说明轴承出现故障，但是依靠均方根值难以诊断早期故障。

本文选取5 380 min时采集的10 000点数据进行分析，时域波形及其包络谱如图9所示，时域波形中不能观察出周期性的故障冲击，包络谱中没有明显的外圈故障频率fo，不能说明发生了外圈故障，同时也说明故障处于早期阶段。对该信号应用中心频率观察法进行VMD分解，当K=5时各分量的归一化中心频率如表3所示，分量IMF4峭度（7.653 1）最大，选为最优分量。图10为IMF4的时域波形和包络谱，从包络谱可以看出，VMD方法能够分解出230Hz的外圈故障频率fo，说明VMD算法具有较高的分解准确度，但图中仍有一定的干扰频率成分，尤其是493Hz频率易造成误诊，需要进一步滤波处理。通过快速谱峭度计算选取最优中心频率为5625Hz，带宽为750Hz，对最优分量IMF4进行带通滤波得到滤波信号的时域波形及其包络谱如图11所示，时域波形中周期性冲击成分更为明显，包络谱中fo、2fo的外圈故障频率清晰可见，且干扰频率很少，能够准确地判定轴承发生了外圈故障，实现了早期外圈故障诊断，也充分说明了本文方法的有效性。

表2 滚动轴承结构参数

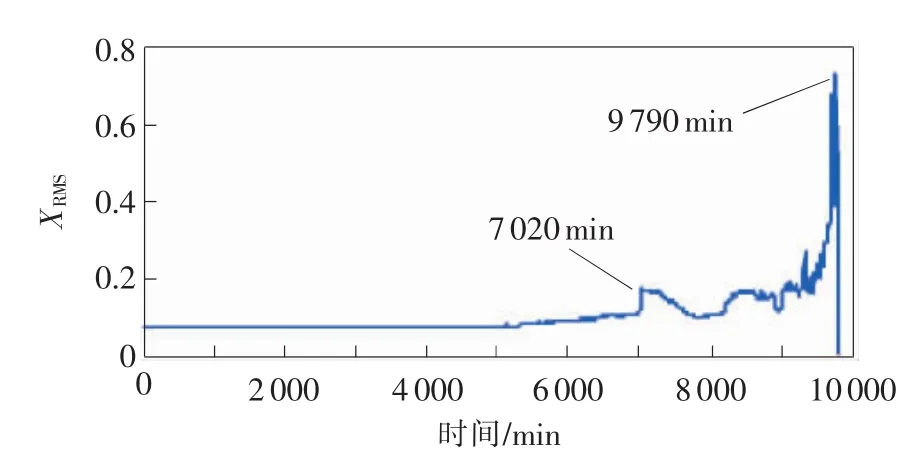
图8 故障轴承垂直方向振动信号均方根值趋势图

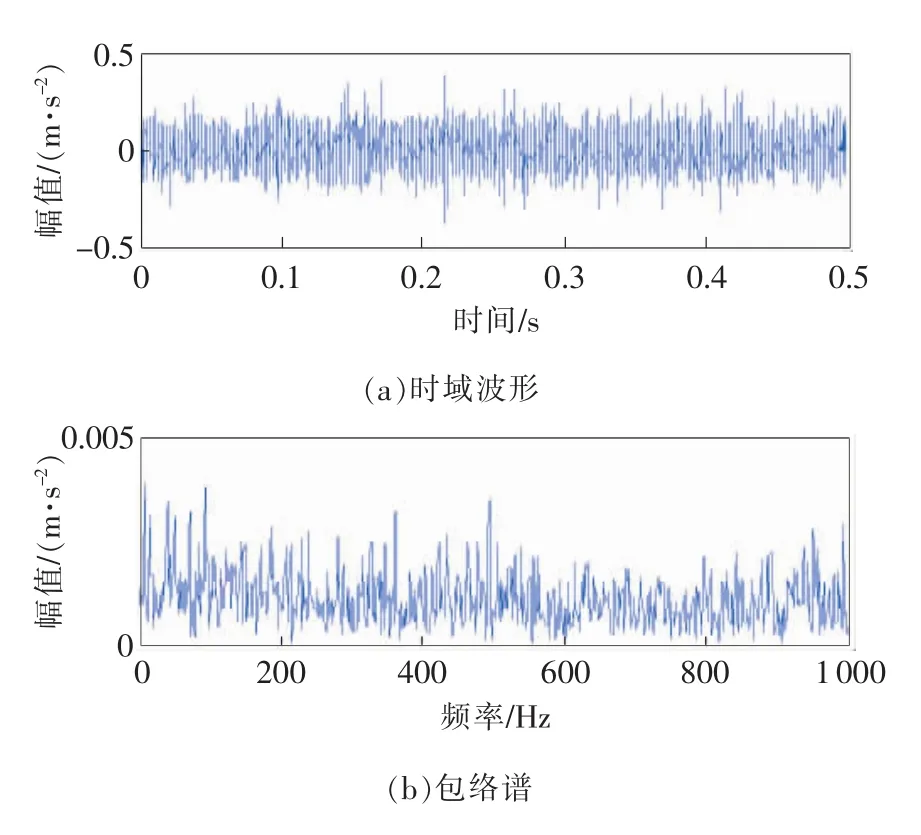
图9 外圈故障振动信号的时域波形和包络谱

表3 K=5时各分量的归一化中心频率

图10 分量IMF4的时域波形和包络谱

图11 分量IMF4经FSK滤波后的时域波形和包络谱

为了与本文方法分析效果进行对比，对早期外圈故障信号进行EMD分解，峭度值最大的分量及其包络解调如图12所示，包络谱中虽然能够看到fo的外圈故障频率，但其幅值相对较小，不能准确、可靠地诊断早期轴承外圈故障，分析效果较本文方法差。

图12 EMD中峭度最大分量的时域波形和包络谱

4 结束语

VMD采用频域非递归的变分分解模式，分解准确度高，以峭度为准则选出VMD分解轴承振动信号的最优分量再进行FSK计算和带通滤波，能够准确提取滚动轴承故障冲击成分，最后通过分析滤波信号包络谱中故障频率实现早期轴承故障的诊断，分析效果比直接包络分析与基于EMD的包络分析好，可为轴承早期故障诊断提供参考。

[1]莫代一，崔玲丽，王婧.基于双重Q因子的稀疏分解法在滚动轴承早期故障诊断中的应用[J].机械工程学报，2013，49（9）：37-41.

[2]苏文胜，王奉涛，张志新，等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击，2010，29（3）：18-21.

[3]向玲，鄢小安.汽轮机转子故障诊断中LMD法和EMD法的性能对比研究[J].动力工程学报，2014，34（12）：945-951.

[4]刘志川，唐力伟，曹立军.基于MED及FSK的滚动轴承微弱故障特征提取[J].振动与冲击，2014，33（14）：137-142.

[5]DRAGOMIRETSKIY K，ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[6]刘长良，武英杰，甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报，2015，35（13）：3358-3365.

[7]唐贵基，王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报，2015，49（5）：73-81.

[8]刘尚坤，唐贵基.改进的VMD方法及其在转子故障诊断中的应用[J].动力工程学报，2016，36（6）：448-453.

[9]彭畅，柏林，谢小亮.基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J].振动与冲击，2012（20）：143-146.

[10]WANG Y，MARKERT R.Filter bank property of variational mode decomposition and its applications[J].Signal Processing，2016（120）：509-521.

[11]ANTONI J. Fast computation of the kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing，2007，21（1）：108-124.

[12]QIU H， LEE J， LIN J， et al.Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J].Journal of Sound and Vibration，2006，289（4/5）：1066-1090.

（编辑：李妮）

Incipient fault diagnosis method for rolling bearing based on VMD and spectral kurtosis

TANG Guiji，LIU Shangkun
（Department of Mechanical Engineering，North China Electric Power University，Baoding 071003，China）

As the problem of the fault signal of rolling bearing is a multi-component and nonstationary vibration signal，which is difficult to diagnose when the signal has weak initial features.A fault diagnosis method based on variational mode decomposition （VMD） and spectral kurtosis（SK） was proposed in the paper.Firstly， the vibration signal was decomposed into several component signals by VMD，and the component which had the maximum kurtosis and had the most fault impact components was selected as the optimal component.Then，the fast SK was computed to the optimal component for band pass filtering and highlighting the fault impact components.Finally，the fault was diagnosed by analyzing the fault frequency appeared in the filtered signal envelope spectrum.The experimental analysis results show that the proposed method can diagnose bearing incipient faults effectively and it has certain engineering application value.

variational mode decomposition； fast spectral kurtosis； rolling bearing； incipient fault diagnosis

A

1674-5124（2017）09-0112-06

10.11857/j.issn.1674-5124.2017.09.020

2016-12-03；

2017-02-19

中央高校基本科研业务费专项资金资助项目（2017MS190，2014MS156）；河北省自然科学基金项目（E2014502052）

唐贵基（1962-），男，山东烟台市人，教授，博士，研究方向为机械设备状态监测及故障诊断。