钻孔岩体结构均质区划分方法研究
2017-11-28,,,,
,,,,
(1.西南石油大学 土木与建筑学院, 成都 610500; 2.重庆大学 煤矿灾害动力学与控制国家重点实验室, 重庆 400044;3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071; 4.东华理工大学 地球科学学院,南昌 330013)
钻孔岩体结构均质区划分方法研究
魏翔1,2,杨春和2,3,王贵宾3,陈世万2,霍亮4
(1.西南石油大学 土木与建筑学院, 成都 610500; 2.重庆大学 煤矿灾害动力学与控制国家重点实验室, 重庆 400044;3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071; 4.东华理工大学 地球科学学院,南昌 330013)
岩体结构均质区是针对实际工程特点而划定的成果,在实践过程中需要根据具体工程,抓住主要矛盾后,选择最具影响性的要素作为划分依据。针对高放废物深地质处置工程中钻孔岩体渗透性研究,提出了定性和定量相结合的钻孔岩体结构均质区划分方法。研究表明:基于结构面力学成因的定性岩体结构均质区划分方法存在对破碎带和蚀变带等细节考虑不足的问题,而以定量分区为主的岩体结构统计均质区划分方法(Miller法),未考虑影响岩体渗透性的主要因素结构面隙宽。最后得出将定性和定量相结合的方法来确定均质区效果更佳,这样既可以考虑到更多的结构面参数,同时也可以细化分区范围。此均质区划分方法结果能为后续的结构面网络建模及渗流计算提供数据支持。
岩体结构;均质区划分方法;力学成因;Miller法;定性与定量相结合的方法
1 研究背景
在地下工程中,结构面空间分布规律的不同,使得地下不同部位的地质、地质力学和水文地质特征等存在差异。因此,在进行地下工程结构面调查时,确定岩体结构均质区是很有必要的工作[1]。
岩体结构均质区划分旨在找出相似结构岩体的边界,将研究区划分为若干个具有相似地质力学性质的独立区域,使每个区域内岩体具有相似的结构特征和地质力学性质[2-6]。目前岩体均质区主要基于结构面几何参数调查统计来确定。因此,提出了一系列成熟的划分岩体结构统计均质区的方法。Stanley和Miller[2]认为对于一般工程来说产状是结构面的主要因素,提出了采用结构面产状为指标进行岩体结构统计均质区划分的方法,即Miller法;肖尚斌等[1]以Miller法的岩体结构分区原理为基础,提出了依据结构面产状和密度2项指标的岩体结构统计均质区划分方法;范留明等[6]在西南某大型水电站工程中,选择结构面密度作为划分均质区的依据,提出了1种基于结构面密度的岩体结构统计均质区划分方法,即密度分区方法,并证明了该方法的可行性;高敬等[7]针对高放废物地质处置预选区2个重点问题核素迁移和围岩稳定,选择了以产状为主迹长和以密度为辅的花岗岩体内结构统计均质区划分;张文等[8]考虑了结构面的产状(倾向、倾角)、迹长、张开度、起伏状态,通过列联表卡方检验法实现了对裂隙岩体结构统计均质区的划分。
岩体中结构面的空间分布是变化的,在高放废物深地质处置工程中,岩体结构合理分区对节理三维网络模拟和岩体渗流特征等工作有重要意义。已有的均质区划分方法是在结构面特征调查的基础上通过各种几何参数在统计上的相对均质来确定均质区的。但是在研究钻孔结构面发育区段的岩体渗透特征时,根据渗透张量计算公式[9]可知,隙宽是影响渗透张量的主要参数。传统方法可以通过岩心直接测量结构面隙宽,但工作量巨大且精度较低,钻孔电视对规模较大的近垂直结构面测得的隙宽远大于实际岩心测得的隙宽[10]。因此,利用结构面调查统计来定量确定钻孔岩体结构均质区存在一定的误差。鉴于此,本文提出依据结构面的力学成因的定性钻孔岩体结构均质区划分方法,并分析将定性法和定量法相结合来确定钻孔岩体结构均质区的优势。
2 结构面力学成因
岩体是地质体,它经历过多次反复地质作用,经受过变形,遭受过破坏,形成一定的岩石成份和结构,其包括结构面、结构体和赋存条件。岩体中结构面是通过原生建造、构造改造和表生改造3个阶段综合作用形成的产物。根据结构面的形成成因,将其分为3种类型:原生结构面、构造结构面和次生结构面[11]。在研究钻孔结构面发育区段的岩体渗透特征时,主要以构造结构面为研究对象。
根据构造地质学,岩石在断裂过程中产生的构造统称为断裂构造。凡是断裂两侧的岩石沿断裂面没有位移或仅有微量位移的断裂,称为节理;而沿断裂面发生较大位移的则为断层。针对钻孔岩体而言,主要对节理进行调查统计。任何节理都是在一定的条件下受了力的作用而产生的,根据节理的力学成因,可将其分为剪节理和张节理[12]。
2.1 剪节理
剪节理是在应力作用下剪切面进一步发展而成,一般剪节理成对出现,形成共轭的X型节理(图1)。

图1 共轭的X型节理Fig.1 X-shaped conjugate shear joints
(1) 剪节理产状较稳定,沿走向延伸较远,常常切过砾岩中的砾石或岩层中的化石而不变方位,剪节理产状基本一致。
(2) 剪节理为剪破裂产生,平行破裂面发生一定量的相对位移,因此剪节理面平直光滑,且多紧闭。但由于后期风化或地下水的溶蚀作用可以扩大节理张开度。
(3) 剪节理一般发育较密,常密集成带。
(4) 根据剪节理方位可以推测节理形成的主压应力方位(图1(b)),同时通过应力场也可以确定剪节理方位(图1(c))。
2.2 张节理
张节理是由于张性破裂所产生,其两侧相对位移垂直于破裂面,剪切分量为0。因此张节理面是张开的,多数情况下为各种矿物填充。根据其力学成因可知,张节理具有如下特征:
(1) 张节理产状不甚稳定,往往延伸较短,单个节理短而弯曲。
(2) 张节理面粗糙不平,且被岩脉充填,其两壁之间距离较大(图2)。
(3) 张节理一般发育稀疏,节理间距较大,而且即使局部地段发育较多,也是稀疏不均,很少有密集带。
(4) 根据张节理方位可以推测节理形成的拉应力方向,同时通过应力场也可以确定张节理方位(图2)。
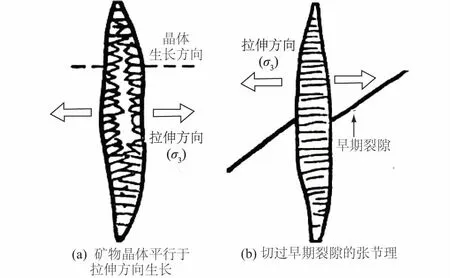
图2 张节理Fig.2 Tensile joints
3 基于结构面力学成因的岩体结构均质区划分
岩体构造结构面是在构造应力场作用下形成和发育的,构造应力是岩体结构形成的根本控制因素。因此,对岩体结构面的研究应建立在岩体应力水平调查的基础上[13]。本文以高放废物地质处置新疆预选区某一钻孔为研究对象,对钻孔进行了水压致裂法地应力测量,并根据应力水平进行均质区划分。
3.1 钻孔岩体应力水平研究
钻孔位于新疆,孔深700 m,孔径为95 mm。钻孔揭露显示,该钻孔地层岩性主要为二长花岗岩,岩芯总体完整。综合钻探时水位、水文试验时水位、地应力测量时水位,确定地应力计算时静水位为75.00 m,试验段长度均为0.80 m。
表1为钻孔中20个深度处水压致裂地应力测量结果。水压致裂应力测量理论[14]表明,水压致裂产生的破裂方向就是最大水平主压应力的方向。
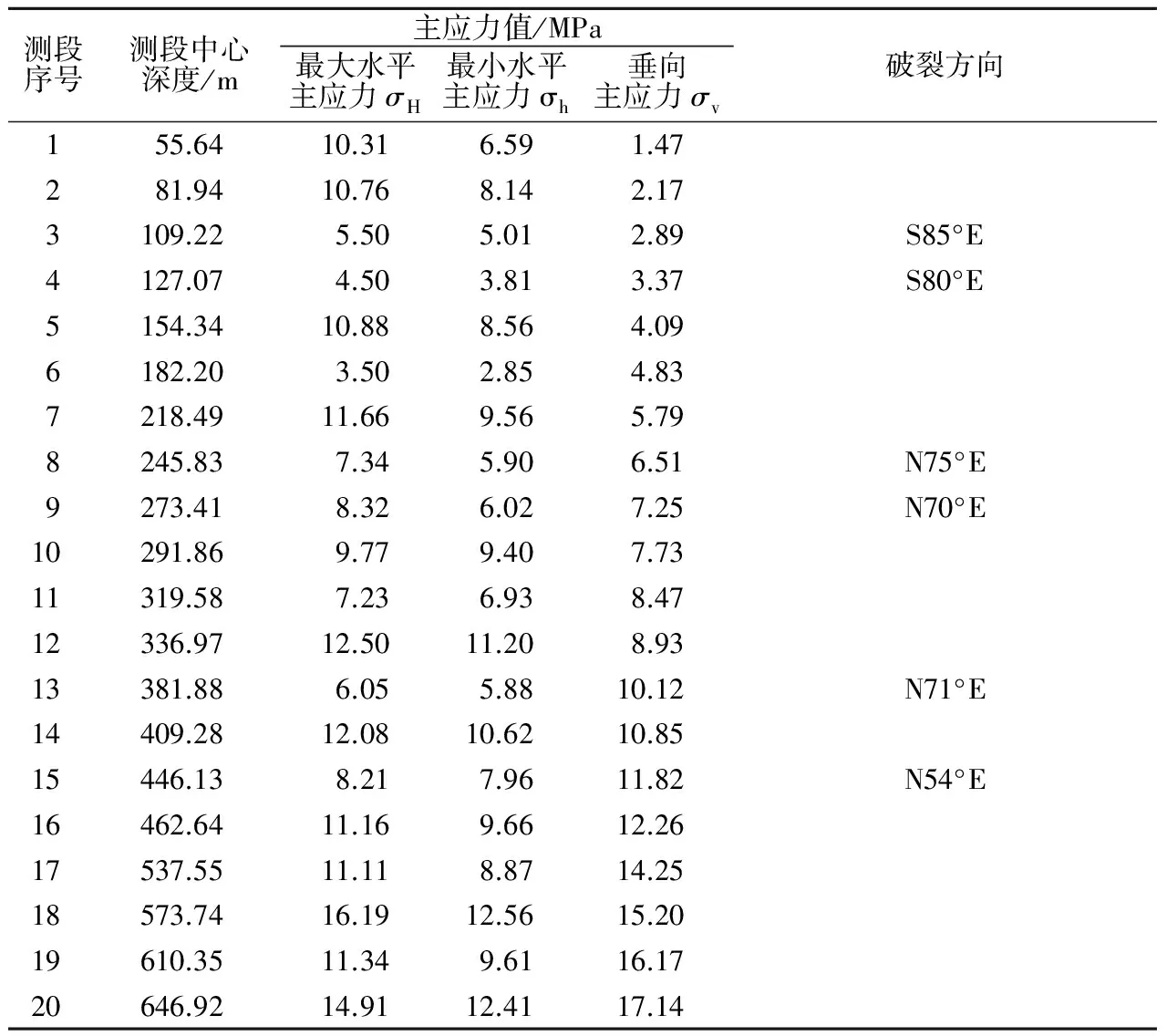
表1 钻孔水压致裂地应力测量结果Table 1 Test results of in-situ geostress in the borehole by hydrofracturing method
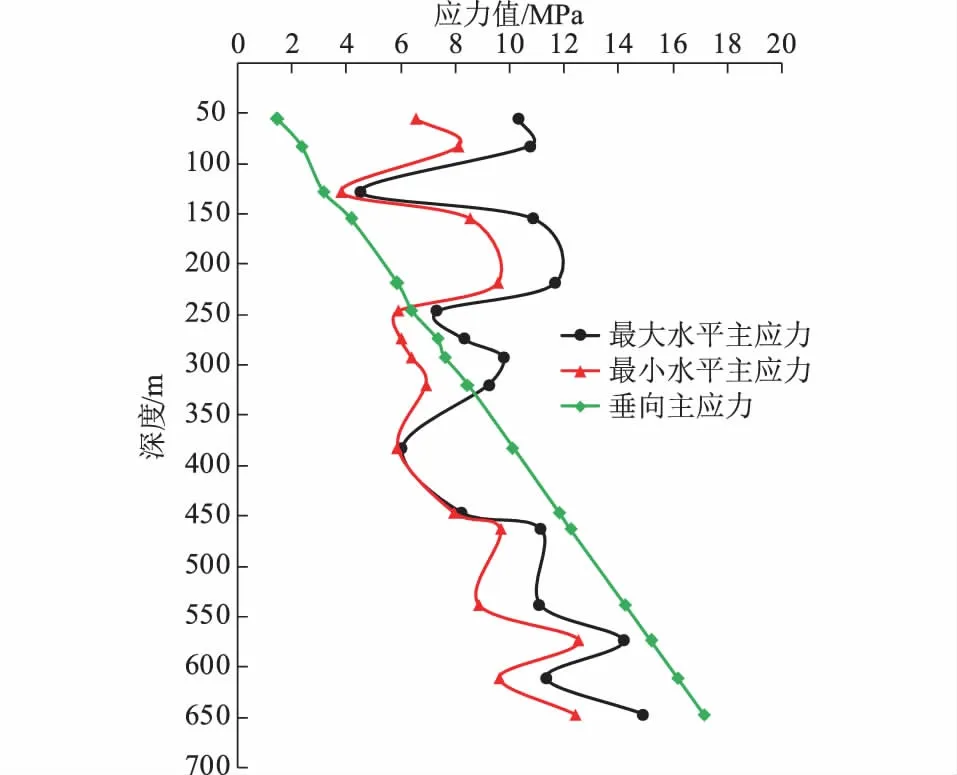
图3 应力值与深度的关系Fig.3 Relationship between stress and depth
图3给出了应力值随深度的变化,可以看出:大致在深度220 m以上,3个主应力的关系总体表现为σHgt;σhgt;σv,表明该深度以上应力场以水平主应力作用为主导;而在180 m左右出现垂向应力最大是由于该区域出现破碎带导致的;大致在[220,420] m深度,3个主应力间的关系总体表现为σHgt;σvgt;σh,表明该深度以最大水平主应力和垂直应力相互作用为主。大致在[420,700] m深度,3个主应力间的关系总体表现为σvgt;σHgt;σh,该深度主要以垂直应力作用为主导。
3.2 钻孔岩体结构均质区划分
根据结构面力学成因可知,钻孔在220 m深度以上,以水平主应力作用为主导,其最大主应力方向在S80°E附近,易形成缓倾角剪节理和近水平张节理(图4),剪节理走向大致为NEE和NWW两组。
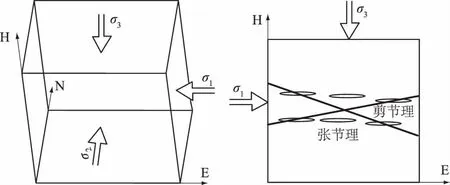
(a)立体图 (b)剖面图图4 钻孔在[0,220]m深度的节理形态Fig.4 Morphology of joints at depth range [0,220]m
钻孔在[220,420]m深度之间,根据3个主应力大小关系和最大主应力方向可知,岩体形成缓倾角剪节理和陡倾角张节理(图5),剪节理走向大致为NE和SE两组,张节理走向大致以SE为主。

(a)立体图 (b)剖面图图5 钻孔在[220,420]m深度的节理形态Fig.5 Morphology of joints at depth range [220,420]m
钻孔在[420,700] m深度,垂直应力作用为主导,岩体形成陡倾角剪节理和陡倾角张节理(图6),剪节理走向大致为SE附近,张节理走向大致也在SE附近。
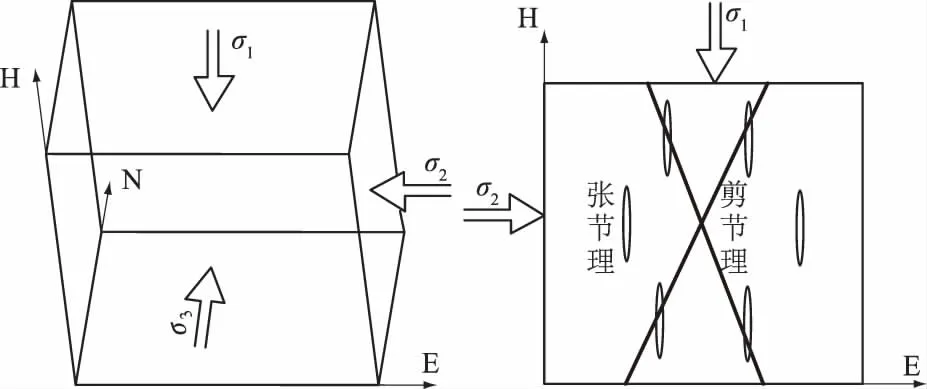
(a)立体图 (b)剖面图图6 钻孔在[420,700]m深度的节理形态Fig.6 Morphology of joints at depth range [420,700]m
结构面间距是指同一组结构面相邻结构面之间的垂直距离。由于岩性、多期构造运动迭加、应力不均匀分布和岩层厚度等多种因素综合作用影响,使结构面间距分布十分复杂。根据室内岩石力学试验[14],岩性不同,岩体力学和物理特性有较大差异,且岩石的抗拉强度远小于抗剪强度,前者约为后者的1/3。随着钻孔深度的增加,岩体将由二维应力状态转为三维应力状态,其发生拉伸破坏的机会较小,最主要的破坏形式是剪切破坏。因此,随着深度的增加,张节理数量减少,间距逐渐变大,而缓倾角剪节理随垂向应力逐渐增加,其数量逐渐减少,陡倾角剪节理受应力影响相对较少。
结构面隙宽是指张开结构面两壁之间的垂直距离。结构面是在特定应力作用形成的,结构面隙宽与应力状态相关,徐光黎[15]根据结构面的法向变形性质,得出在某一应力场作用下,应力与隙宽的关系式为
E=E0-σijninj/Rn。
(1)
式中:E0为初始隙宽;σij为有效应力张量;Rn为法向刚度。
根据式(1),徐光黎[15]还推导了结构面隙宽随深度的变化关系式,即
E=E0-mz/(n+z) 。
(2)
式中:z为钻孔深度;m和n为与岩石有关的常数。
根据式(2)可知,结构面隙宽随深度增加而逐渐减小,但是衰减速度逐渐变慢。
因此,可将钻孔划分为[0,220],[220,420]和[420,700] m 3个均质区。
4 基于Miller法的的岩体结构均质区划分
1977年,国际岩石力学学会野外实验方法标准化委员会(现称实验方法委员会)建议使用产状、间距、迹长、粗糙度、张开度、充填胶结特征、面壁抗压强度、渗流、组数和块体大小10个参数描述岩体结构面[16]。在岩体结构统计均质区确定时,原则上应该把描述岩体结构面全部参数进行均质区划分,但是实现比较困难,既费时又耗力。因此,在划分均质区时,要综合考虑工程的具体需要和实际操作的实现情况,选择最具影响性的要素作为划分依据。目前,由于结构面产状容易通过测量获得,因此用结构面产状来描述岩体结构均质区是广泛应用的方法。
针对以结构面产状为要素的均质区划分,1983年Stanlty和Miller[2]采用概率论中的列联表和施密特等面积投影网结合的办法,利用卡方检验分析相关性,来确定以结构面产状为指标进行岩体结构均质分区。本文利用钻孔电视调查的结构面产状,采用Miller法对钻孔岩体进行了统计均质区划分见表2,最终将钻孔划分为[0 ,180],(180,220],(220,500]和(500,700]m 4个均质区。
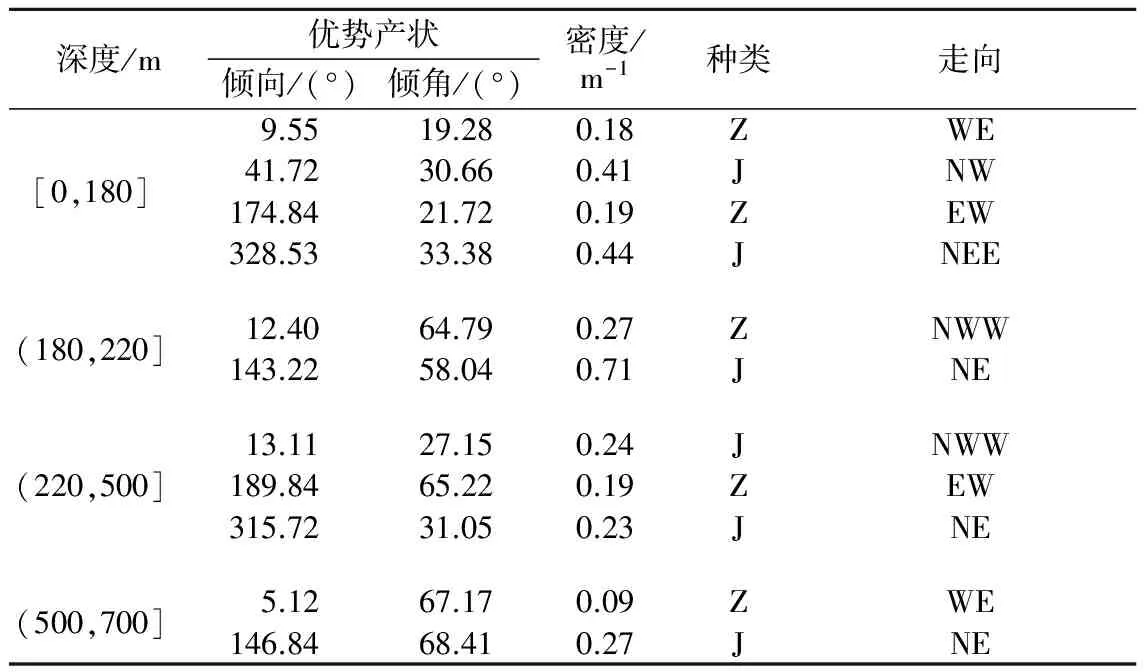
表2 钻孔节理优势产状Table 2 Dominant attitudes of joints in the borehole
注:J代表剪节理,Z代表张节理
5 讨 论
根据结构面力学成因可以定性划分钻孔岩体结构均质区,基于Miller法可以定量确定钻孔岩体结构均质区,但是通过2种方法得出的均质区结果存在一定的差异。这主要是由于定性法存在对破碎带和蚀变带等细节考虑不足的问题,而定量法未考虑影响岩体渗透性的主要因素结构面隙宽。因此通过将定性法和定量法相结合来确定钻孔岩体结构均质区,这样既可以更加细化分区范围,也可以避免单一划分方法存在的不足。具体表现为:
(1) 钻孔深度在[0,220] m区间,利用定性法将其作为一个均质区,在此区间岩体主要发育陡倾角结构面;而根据定量法将该区间分为[0,180] m和 (180,220] m 2个均质区。这是由于在[0,180] m深度即地表是在外力(如风化、地下水、卸荷等)的作用而形成的次生陡倾角结构面;在(180,220] m深度,由于岩体处于破碎带,结构面比较发育,导致岩体应力状态重新分布来达到平衡。因此通过定性和定量法相结合将钻孔该深度区间划分为[0,180] m和 (180,220] m两个均质区。
(2) 钻孔深度在(220,500] m区间,利用定量法将其作为一个均质区,而根据定性法将其分为(220,420] m和 (420,500] m 2个均质区。这是由于钻孔(420,500] m深度处于由水平最大主应力向垂直最大主应力转变的过渡带,缓倾角剪节理随着垂向应力增加而逐渐减少,过渡带还是发育缓倾角结构面为主,但是该深度与(220,420] m深度的应力方向不同。因此通过定性和定量法相结合将钻孔该深度区间划分为(220,420] m和 (420,500] m 2个均质区。
因此可以将钻孔划分为[0,180],(180,220],(220,420],(420,500],(500,700] m 5个均质区。这样分区结果为后续的结构面网络建模及渗流计算提供更加准确和合理的数据支持。
6 结 论
岩体结构均质区是针对实际工程需要而划定的成果,在实践过程中必须针对具体性的要素作为划分依据。在对钻孔岩体进行渗透性分析时,提出了基于结构面力学成因的定性岩体结构均质区划分和以定量分区为主的岩体结构统计均质区划分方法(Miller法),通过对2种方法比较得出如下结论:
(1) 结构面是在一定的应力条件下产生的,利用水压致裂测得钻孔岩体的应力状态,根据结构面力学成因对钻孔岩体进行结构均质区划分。
(2) 利用钻孔电视调查统计结构面产状,采用Miller法(以产状为主要因素)确定了钻孔岩体结构统计均质区。
(3) 2种方法分别以定性和定量来确定均质区,将2种方法相结合能很好地弥补各自的不足并使划分结果更加合理。
上述钻孔岩体结构均质区划分为后期岩体渗透特征提供了依据,而钻孔岩体结构还受环境和人为等不确定因素影响。因此,岩体结构均质区划分方法还有待进一步深入研究。
[1] 肖尚斌,张艳君,郑美霞.蒲石河抽水蓄能电站地下厂房区岩体结构统计均质区划分[J].东北水利水电,1997,35(8):39-41.
[2] STANLEY M, MILLER A. Statistical Method to Evaluate Homogeneity of Structural Populations [J]. Mathematical Geology, 1983, 15(2): 317-328.
[3] KULATILAKE P H S W. Bivariate Normal Distribution Fitting on Discontinuity Orientation Clusters[J]. Mathematical Geology, 1986, 18(2): 181-195.
[4] KULATILAKE P H S W,FIEDLER R, PANDA B B. Box Fractal Dimension as a Measure of Statistical Homogeneity of Jointed Rock Masses[J]. Engineering Geology, 1997, 48: 217-229.
[5] BINGHAM C. Distributions on the Sphere and on the Projective Plane[D].New Haven: Yale University,1964.
[6] 范留明,黄润秋,丁秀美.一种基于结构面密度的岩体结构均质区划分方法[J].岩石力学与工程学报,2003,22(7):1132-1136.
[7] 高 敬,杨春和,王贵宾.甘肃北山岩体结构均质区划分方法的探讨[J].岩土力学,2010, 31(2): 588-592,598.
[8] 张 文,陈剑平,刘存合,等. 卡方检验在裂隙岩体统计均质区划分中的应用研究[J]. 岩土工程学报,2011, 33(9): 1440-1446.
[9] 田开铭,万 力.各向异性裂隙介质渗透性的研究与评价[M].北京:学苑出版社,1989.
[10] 王锡勇,苏 锐,陈 亮,等. 基于超声波钻孔电视的深部岩体结构面特征研究[J].世界核地质科学, 2014, 31(1): 39-44,62.
[11] 蔡美峰. 岩石力学与工程[M].北京:科学出版社,2002.
[12] 刘春原,朱济祥,郭抗美.工程地质学[M].北京:中国建材工业出版社,2000.
[13] 黄润秋. 复杂岩体结构精细描述及其工程应用[M].北京:科学出版社,2004.
[14] 朱焕春,陶振宇.不同岩石中地应力分布[J].地震学报,1994,16(1):49-63.
[15] 徐光黎. 节理张开度水力学分析[J]. 勘察科学技术,1993,(2):3-6.
[16] International of Society of Rock Mechanics.Suggested Method for the Quantitative Description of Discontinuities in Rock Masses[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1978, 15(6): 319-368.
(编辑:刘运飞)
Dividing Structural Homogeneity of Rock Mass by Using Boreholes
WEI Xiang1,2, YANG Chun-he2,3, WANG Gui-bin3,CHEN Shi-wan2, HUO Liang4
(1.School of Civil Engineering and Architecture,Southwest Petroleum University, Chengdu 610500,China; 2.State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China; 3.State Key laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics of Chinese Academy of Sciences, Wuhan 430071, China; 4. School of Earth Sciences, East China University of Technology, Nanchang 330013, China)
Structural homogeneity of rock mass is divided according to project features. In practice, we must choose influential elements of the project as the basis of dividing. In this article, a method integrating qualitative and quantitative approaches of dividing structural homogeneity of rock mass is put forward for researching the permeability of
rock mass with boreholes for deep geological disposal of high-level radioactive waste. Research results revealed that fracture and alteration zone were not fully taken into account in the qualitative method based on mechanical causes of structural plane. On the other hand, in quantitative method such as Miller method, fracture width as a major factor affecting the permeability of rock mass was ignored. In conclusion, to combining qualitative and quantitative methods could achieve better results by taking into account more parameters of structural plane as well as more detailed dividing parts. The proposed method provides data support for subsequent network modeling and seepage calculation.
rock mass structure; dividing method for homogeneous area; mechanical causes; Miller method; combining qualitative and quantitative method
2016-07-04;
2016-08-10
国家自然科学基金项目 (51104144)
10.11988/ckyyb.20160678 2017,34(11):72-76,83
TU45
A
1001-5485(2017)11-0072-05
