基于马尔科夫过程的高堆石坝施工度汛决策模型

，， ，

(三峡大学 水利与环境学院，湖北 宜昌 443002)

基于马尔科夫过程的高堆石坝施工度汛决策模型

刘潋，胡安娜，宋玲，罗舒

(三峡大学 水利与环境学院，湖北 宜昌 443002)

高堆石坝施工挡水风险的时变性和填筑进度的不确定性增加了坝体施工期度汛方案决策的难度。针对高堆石坝施工度汛过程动态变化的特点，随机模拟大坝挡水风险，并将其划分3个风险状态以判断度汛行动。以整个度汛施工期成本最小化为目标，考虑洪水来流、填筑进度和决策成本等关键因素，建立基于马尔科夫过程的高堆石坝施工度汛决策模型，分析逐月大坝挡水风险状态下的度汛策略、成本函数和风险状态转移概率。在检验其马尔科夫特性基础上，采用决策迭代算法求解每一决策时刻状态下的最优施工度汛方案及度汛过程的决策路径。工程实例分析表明，该决策模型对高堆石坝施工度汛计划策略的调控结果符合实际施工度汛高程变化情况，为指导快速准确制定大坝施工度汛方案提供了参考。

高堆石坝；施工度汛；风险决策；马尔科夫过程；成本最小化

1 研究背景

高堆石坝多集中在高山峡谷地区，洪枯水位流量变化幅度大、填筑周期长[1]。与其他坝型相比，高堆石坝汛期施工考虑因素更多，尤其在大坝高程高于围堰高程后，度汛方案与时空联系紧密，决策难度更大。寻求科学的决策方法来有效、实时控制风险，确保大坝在汛期安全经济施工显得尤为重要。近年来，施工导流度汛决策研究取得了一系列进展。范锡峨等[2]、Rasekh等[3]关注导流风险与收益间的关系，建立了基于效用函数的导流方案多目标决策模型；钟登华等[4]根据期望值、风险承受能力评价施工导流方案；张超[5]计算了高堆石坝中期度汛挡水风险，为中期度汛标准的确定提供了参考；李宗坤等[6]建立基于改进突变评价法的土石坝施工期风险评价模型；刘潋等[7]考虑施工进度对风险交互影响，构建挡水风险自适应动态控制模型；薛进平等[8]将单一主体风险预期下的决策行为拓展为多元主体，引入协商机制解决群体参与下的施工导流度汛决策问题。上述研究大多针对施工过程中单一或关键节点进行度汛风险分析及方案的评价和择优。

针对高堆石坝施工度汛过程的时序动态变化的特性，考虑洪水来流、填筑进度、漫顶损失等因素的影响，提炼度汛决策过程的马尔科夫特性和参数表达，构建基于马尔科夫过程的高堆石坝施工度汛决策模型，运用迭代决策法求解度汛最优决策路径，为高堆石坝施工度汛措施方案的优选提供方法支撑。

2 高堆石坝施工度汛决策特征分析

2.1 度汛动态决策理论

为实现高堆石坝施工度汛风险实时调控，将马尔科夫过程模型引入到施工度汛动态决策中。马尔科夫过程是一种描述复杂系统状态转移的数学模型，其特点是：当前的决策时刻的系统状态只与前一个决策时刻状态和行动有关，与更早决策时的状态和行动独立[9]。因此，可以根据当前状态和发展趋势预测未来状态发生及决策过程。高堆石坝施工汛期来临前需要做出临时施工资源调度决策，决策者需要根据水文预测或洪水预报及现阶段施工进度情况确定下一阶段的度汛方案。除此之外，随着大坝施工面貌的变化，也要根据上一阶段实施方案的效果和目前的状况，多阶段制定决策向量。因此，高堆石坝度汛可看作一个马尔科夫决策过程。

2.2 度汛风险定义

高堆石坝施工度汛风险率是确定施工导流方案的关键因素之一。本文定义度汛风险为：入汛后当坝体修建到围堰高程以上，决策时间点n的坝前水位超过该时间点所达到的填筑高程的概率，如式(1)所示。

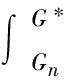
(1)

式中：P(n)为高堆石坝施工度汛风险率；Dn为n时刻洪水来流量预测；Hn为随机模拟得到的坝前最高水位；Gn为计划填筑的挡水高程；G*为高堆石坝的设计高程；f(H|D)为D发生条件下的n时刻坝前水位概率密度函数。

直接求解坝前水位分布函数困难，因此采取蒙特卡罗(MC)随机模拟方法[10]。以P-Ⅲ分布作为洪水序列(洪量)分布，泄流能力参数假设仅受到泄流建筑物糙率影响，其服从三角分布，大坝挡水高程可以通过施工进度计划获取。

高堆石坝风险率模拟过程为：①汛期来临前的当月月末为计算起始点；②确定下月洪水序列分布参数和MC方法的模拟次数M；③生成洪水过程随机数并模拟下月决策时间点n的来流；④生成泄流能力参数随机数，拟合泄流曲线；⑤结合泄流过程线和洪水过程线，经调洪演算模拟出坝前最高水位Hn；⑥比较Hn和下月计划高程Gn；⑦通过反复模拟，统计出Hn超过Gn的次数为MR，则第n个月的挡水风险P(n)=MR/M；⑧回到步骤②计算下月挡水风险P(n+1)，直至Gn=G*。

2.3 度汛方案成本分析

施工度汛主要采取3种策略：加快填筑进度，坝面过流度汛以及按原计划施工[11]。当高堆石坝挡水高程高于围堰高程时，其决策成本函数为Lk(k为策略序号，k=1,2,3)。为最大程度减少其他因素对成本的影响，本文只考虑单一决策的成本函数。

(1)加快挡水高程填筑进度。该策略在汛前加大了大坝填筑强度以减小风险，但增加了额外的资源和成本，其成本函数L1如式(2)所示。

L1=-Cq(n,Δh)-Cp(n,Δh) 。

(2)

式中：Cq为加快进度额外增加的成本，例如夜间施工消耗的人工和机械成本；Cp为在有限资源条件下的机会成本。L1与决策时间节点n和该月水位上升高度Δh相关。

(2)坝面过流保护。当坝高在施工过程中低于临时防洪标准时，可采取坝面过水措施。这种情况下，坝面停止填筑作业进行防止过流侵蚀坝面的保护措施。通常在整个或部分坝面上采用钢筋笼、砂浆、干砌石作为保护，或预留缺口、或设置溢流槽。停工进行坝面保护导致进度延迟，使得蓄水发电时间推后，且发电效益下降，故该策略成本函数L2如式(3)所示。

L2=-(C1+C2+C3) 。

(3)

式中：C1为用于围堰和大坝保护的钢筋笼、砂浆和干砌石工程量与单位价格的乘积；C2为清理费用；C3为工期成本，主要包括发电量损失。

(3)按原进度计划施工。如本月计划上升高度若可满足防洪要求，可按原施工进度计划进行度汛策略选择。尽管该策略节省了赶工和保护成本，但一旦超标洪水发生，决策者需要承担漫坝风险损失。该策略成本函数L3如式(4)所示。

(4)

式中：Cfi为当大坝遭遇超标洪水时未能采取坝面保护措施和风险预警措施时的损失，包括坝面清理与修复成本Cf1，淹没区域的社会经济损失Cf2(如果形成溃坝洪水)以及工期损失Cf3。Cf1，Cf3分别与C1，C3的计算基数相同，Cf2计算如式(5)所示。

(5)

式中：Cy为灾害救援费用；δ为间接损失系数；S为淹没区个数；βi为第i个淹没区每hm2损失率；Vi为第i个淹没区的淹没面积。

3 高堆石坝施工度汛决策模型构建

3.1 参数设计

将高堆石坝施工度汛过程进行分解，汛期从t0到tn划分n个决策时间点(以月为时间间隔)，通过设定5个参数(X,P,A,R,V)构建离散时间动态决策数学模型。

(1)X(tn)=i(i=1,2,3)表示汛期施工过程中大坝的3种风险状态集合，按P(t)的大小归类。

(2)A(i)=ak(k=1,2,3)为度汛行动集合，包括：①加快临时挡水断面的填筑速度；②坝面过流保护措施；③按原施工计划实施。不同风险状态下的度汛行动可组成策略向量Π(i),Π(i)∈A(i)。

(3)P=[Pij]为转移概率矩阵，Pij=P{X(tn)=j|X(tn-1)=i,A(i) }(i,j=1,2,…,m)表示在tn通过行动A(i) (n=0,1…)使得状态i转移到j的概率，可通过经验估计或统计手段获取。

(4)R(i,Π(i))=Rk为回报函数，表示决策者采取策略Π(i)从状态i转移到状态j时的预期收益或成本。影响回报函数的因素有挡水风险、进度(发电)收益或损失、漫坝损失、过流保护措施成本等。

(5)在度汛方案决策时，要共同考虑当前和未来的决策回报。VΠ(n)为第n时刻在i状态下选择策略Π(i)的总成本，令其为目标函数，使其最小。

3.2 马尔科夫检验

检验高堆石坝施工度汛随机过程是否具有马尔科夫性，是应用马尔科夫过程分析的必要前提。通常离散序列的马尔科夫决策过程可以用χ2分布来检验。本文所涉状态集包含m个可能的状态，用Nij表示在(t1,t2,…，tn)时间序列中高堆石坝挡水风险状态从i转移到j的频数。将转移频数矩阵第j列之和除以各行列的总和所得的值称为“边际概率”，记为Pj*，状态i转移到状态j的概率记为Pij，如式(6)所示。

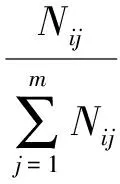
(6)

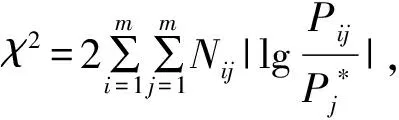
3.3 迭代过程

由于风险状态集X(tn)以及策略Π为有限集，因此可采用折扣公式。通过比较各策略下的折扣总期望收益，运用策略迭代法，在Π中寻找最优策略。首先计算VΠ显式，然后用行动函数QΠ和最优策略函数进行策略改进，如式(7)和式(8)所示。

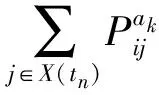
(7)

Π′(i)=arg maxQΠ(i,ak) 。

(8)

式中：QΠ为在状态i下采取行动ak，其他状态采用策略Π的期望回报；γ为折扣因子，0lt;γlt;1。由于策略数目有限，算法经过有限次迭代最终可收敛于最优策略。计算步骤如下：

(1)设定初始值。选取高堆石坝施工原进度计划下的度汛策略作为初始平稳策略Π。

(2)策略求解。通过解m元m次线性方程组求得策略Π下的VΠ函数值，如式(9)所示。

(9)

(3)策略改进。应用式(7)、式(8)，任意组合行动求解，但优先考虑当前初始选定的行动[12-13]。

(4)收敛检验。如果Π′与Π相等，进入步骤(5)，否则令Π=Π′，回到步骤(2)。

(5)返回该时刻下的最优策略Π*。

高堆石坝施工度汛最优决策计算流程见图1。

图1高堆石坝施工度汛决策计算流程

Fig.1Flowchartofdecision-makingforconstructionofhighrock-filldaminfloodperiod

4 算例分析

4.1 项目背景

TK水电站的拦河坝为面板堆石坝，坝顶高程171.00 m，根据施工导流方式，结合进度安排，上下游围堰均采用土石过水围堰型式。围堰的挡水标准为枯水期(10月份—次年4月份)10 a一遇洪水，相应设计流量为2 420 m3/s，过水标准为全年20 a一遇洪水，相应设计流量为10 400 m3/s，结合导流洞泄流。根据施工总进度安排，围堰过水1个汛期后可由坝体临时断面挡水或过水。TK电站施工期导流度汛计划方案如表1所示。

表1 TK水电站施工期导流度汛计划方案

4.2 风险计算

大坝汛期挡水风险分析参数来源分别如下：汛期洪量统计服从P-Ⅲ分布，其均值、变差系数和偏态系数均通过坝址历史洪水资料统计得出；导流系统采用导流隧洞泄流，泄流能力服从三角分布，其分布参数下限a=0.011，中值b=0.015，上限c=0.020；通过对入流流量和泄流流量的随机模拟，结合调洪演算，可以得出分月可能的最高坝前水位Hn+1；通过随机模拟法统计Hn+1超过Gn的次数MR，并除以模拟次数M得出该月的大坝挡水风险率。将汛期施工从第3年10月份至第4年9月份按月划分为8个决策时间点，施工期大坝汛期挡水风险模拟计算结果如表2所示。

表2 不同月份大坝汛期挡水风险计算结果

4.3 月度汛策略

将风险由小到大排列，为符合马尔科夫模型计算要求，经检验，应用聚类法[14]将风险计算结果分为3种状态类型较为合适。结果lt;0.2%为低风险，[0.2%,0.6%]为中等风险，gt;0.6%为高风险。频率矩阵Nij和转移矩阵Pij通过风险状态之间的转移频率获得，如式(10)所示。

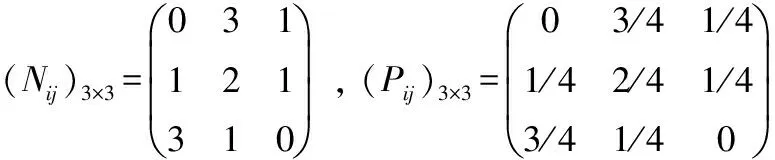
(10)

设定折扣因子γ=0.9，将预期成本最小的一组度汛行动Π0(1)=(a2,a3,a2)作为初始策略。进而采用策略迭代算法进行策略改进，其结果如表4所示。

表3 风险状态转移概率及回报函数结果

表4 策略改进的迭代过程

由表4可知，通过2次迭代找到了不同风险水平下的最优度汛策略。这意味着无论此刻挡水风险大小如何，采用坝面过流方案可确保成本最小，为该时间点的最优度汛策略。

4.4 度汛决策路径

同理，依次得出每个决策时间点的任一状态所对应的最优策略，将最优策略的集合存储在离线策略表中，根据实际每月的风险预测值进行状态划分，查表得到优化后的方案序列，组成施工期度汛决策最优路径，如表5所示。

表5 原度汛决策与优化后决策路径对比

由表5可知，而在洪水流量较小的9—11月份，决策的方案与原计划方案相同，均为计划填筑下的临时坝面挡水，不采取其他防汛措施。而在汛期的第4年的6月份、8月份和9月份二者结果产生差异。6月份原计划的过水变为抢筑，8月份原计划的临时挡水策略变为过水，9月份原计划挡水策略变为加快施工进度抢筑高程，更大程度上减小了施工期度汛成本。在实际工程建设中，TK电站坝体在6—9月份进行了填筑高程的修改，由原计划的30～37 m增加至44 m，恰好符合该模型预测出的在该时间段需要采取高程抢筑的策略。

5 结 语

本文针对高堆石坝施工期当前风险状态，构建基于马尔科夫过程的度汛决策模型，对未来风险状态和度汛方案决策进行预测。算例分析表明，该模型对高堆石坝施工度汛计划策略的调控结果符合实际施工度汛高程变化情况，对确定大坝中后期度汛标准与方案制定以及施工进度计划安排具有一定的指导作用。然而，水电工程施工具有较强的实时性，前一阶段预测的方案执行后的结果对下一阶段风险状态具有反馈影响，在本文中未有考虑。为解决此问题，预测模型必须具备外部环境进行交互的能力，最终实现预测—控制—修正—反馈的决策机制，将是后续研究的侧重点。

[1] 刘 潋,胡志根.时变条件下高堆石坝施工度汛协商决策的演化分析模型[J].水利学报,2013,44(11):1359-1365.

[2] 范锡峨,胡志根,刘 全.基于效用的施工导流方案多目标决策模型[J].中国工程科学,2008, 10(7):137-140.

[3] RASEKH A, AFSHAR A, AFSHAR M. Risk-cost Optimization of Hydraulic Structures: Methodology and Case Study[J].Water Resources Management, 2010, 24(11): 2833-2851.

[4] 钟登华,毛寨汉,刘东海.施工导流方案的多目标总体综合评价方法[J].水利水电技术,2002,33(5): 17-20.

[5] 张 超,胡志根.高堆石坝中期度汛挡水风险率估计[J].水科学进展,2014,25(6):873-879.

[6] 李宗坤,葛 巍,王 娟,等.改进的突变评价法在土石坝施工期风险评价中的应用[J].水利学报, 2014,45(10):1256-1260.

[7] 刘 潋,胡志根.高堆石坝施工度汛挡水风险动态控制模型研究[J].水力发电学报,2015,35(2):82-89.

[8] 薛进平,胡志根,刘 全.施工导流方案动态交互协商决策[J].系统工程理论与实践,2014,34(11):2995-3000.

[9] 刘 克,曹 平.马尔可夫决策过程理论与应用[M].北京:科学出版社,2015.

[10] 胡志根,刘 全, 贺昌海.等.基于Monte-Carlo方法的土石围堰挡水导流风险分析[J].水科学进展,2002,13(5):634-638.

[11] 崔金铁.坝体施工期临时度汛问题探讨[J].水利规划与设计,2006,(2):44-46.

[12] HANSEN E A, ZILBERSTEIN S. LAO*: A Heuristic Search Algorithm that Finds Solutions with Loops[J]. Artificial Intelligence, 2001, 129 (1/2): 35-62.

[13] MOON T, WEISSMAN T. Universal Filtering via Hidden Markov Modeling[J]. IEEE Transactions on Information Theory, 2008, 54(2): 692-708.

[14] 张玉芬,朱雅琳.马尔可夫性及其检验方法研究[J].价值工程,2012,31(2): 312-313.

(编辑：罗 娟)

Decision-making Model for High Rock-fill Dam Construction in Flood Period Based on Markov Process

LIU Lian，HU An-na，SONG Ling，LUO Shu

(College of Hydraulic and Environmental Engineering，Three Gorges University，Yichang 443002，China)

Time variation of water-retaining risk and uncertainty of filling progress aggravate the difficulties in making decision for high rock-fill dam construction in flood period. Accordingly, the water retaining risk of high rock-fill dam was calculated by stochastic simulation, and then was classified into three risk states which could indicate the decision actions. With the objective of minimizing the cost of the entire construction process in flood season, the critical factors such as incoming flood flow, filling schedule and cost of decisions were taken into account to build a decision-making model based on Markov Processes. By using this model, the flood prevention strategies, cost functions and transfer probability for each risk degree were analyzed. After testing the Markov property, the optimal strategy for each state at current time and a sequential risk decision path in this process can be predicted by strategy iteration method. A study case shows that the adjustment results by the proposed model consists well with the actual construction plan change for water retaining elevation. The results offer reference for timely and accurate flood prevention scheme in construction period.

high rock-fill dam; construction in flood period; risk decision making; Markov Process; cost minimizing

10.11988/ckyyb.20160740 2017,34(11):39-43

2016-07-21；

2016-09-05

国家自然科学基金项目(51509143)；长江科学院开放研究基金项目(CKWV2016398/KY)

刘 潋(1986-)，女，湖北宜昌人，讲师，博士，研究方向为水电工程施工与管理，(电话)13986742217(电子信箱)313293608@qq.com。

TV51

A

1001-5485(2017)11-0039-05