流体注入过程中井筒温度场计算及影响因素分析
2017-11-28陈超峰王补信付前进李雪彬胡广文
陈超峰,王补信,付前进,李雪彬,胡广文,刘 奥
(1.中国石油新疆油田公司勘探事业部,新疆 克拉玛依 834000;2.中国石油西部钻探工程有限公司井下作业公司,新疆 克拉玛依 834000;3.长江大学石油工程学院,湖北 武汉 430100)
流体注入过程中井筒温度场计算及影响因素分析
陈超峰1,王补信1,付前进2,李雪彬1,胡广文1,刘 奥3
(1.中国石油新疆油田公司勘探事业部,新疆 克拉玛依 834000;2.中国石油西部钻探工程有限公司井下作业公司,新疆 克拉玛依 834000;3.长江大学石油工程学院,湖北 武汉 430100)
在压裂、酸化等注入过程中,若井筒温度场发生变化,不仅会导致注入流体的性能发生变化,井下管柱、套管也会受到“温度效应”的影响,导致管柱变形。为此我们利用能量守恒定律,建立井筒传热数学模型,并结合计算机技术,对实际生产数据进行计算求解,实现了注入过程中井筒温度场的预测,为注入作业参数的合理选择提供了理论依据。
井筒;温度场;温度;传热
目前,大多数致密、低渗透油气藏常采用大规模的体积压裂及酸化等措施进行储层改造,提高地层渗透率,从而提高单井产量[1]。由于在压裂、酸化等注入过程中,流体温度低于周围环境的温度,随着液体的注入,井筒温度场重新分布,井筒及环空的温度降低[2-4]。因流体注入而产生的“温度效应”,使管柱承受轴向拉力,同时油套环空及套管外环空压力降低,进而影响管柱、套管的强度安全性。注入排量越大,注入时间越长,地面温度越低,井筒及环空的温度降低越多,环空压力降低也越多,管柱安全性受到的影响越大。因此,在油气藏的压裂和酸化过程中,为了保证管柱、套管的强度始终在安全范围内,我们进行了注入过程井筒温度场研究,进一步提高井筒评价和管柱力学的校核精度,为后续工作的进行提供保障。
1 井筒传热模型建立
1.1 井筒传热物理模型
油气井井身结构一般包含表层套管、技术套管、油层套管。表层套管段、技术套管、油层套管外有水泥环,井筒模型如图1所示。
注入过程中,热量的传递过程有以下几个环节:1)油管中的流体在流动时经对流把热量传递给油管内壁;2)经过热传导,热量从油管内壁传递到外壁;3)经对流和热辐射的形式,热量从油管外壁经油管和套管间的环形空间传递到套管内壁;4)经热传导,能量从套管内壁传递到套管外壁;5)最后以导热形式热量从套管外壁经水泥环传到地层。
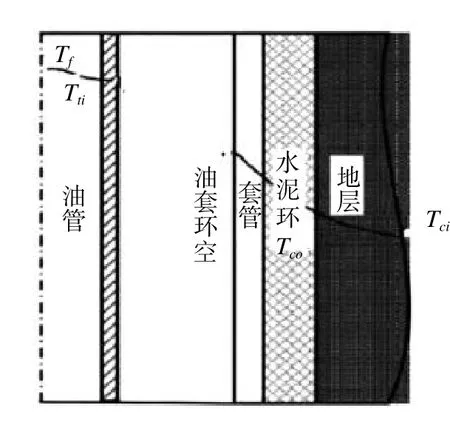
图1 井身结构纵向局部示意
对物理模型的描述和传热过程进行分析,为简化计算,作如下假设:
1)井筒内的传热为稳态传热,周围地层中的传热为非稳态传热,并且满足Ramey[5]无因次时间函数;2)井筒及地层间的传热是径向的,不考虑沿井身方向的传热;3)井筒中任一截面上各点的温度都相等;4)油管、套管和水泥环为同心圆;5)忽略井筒内流体流动过程中的摩擦生热;6)井筒周围地层温度是线性的。
1.2 井筒传热数学模型
以井口为坐标原点,垂直向下为正的坐标系。在油管上取一长为dz的微段,根据能量守恒,从微段进口流入的热量等于从微段出口流出的热量与微段向套管和地层接触面间传递的热量之和(图2)。
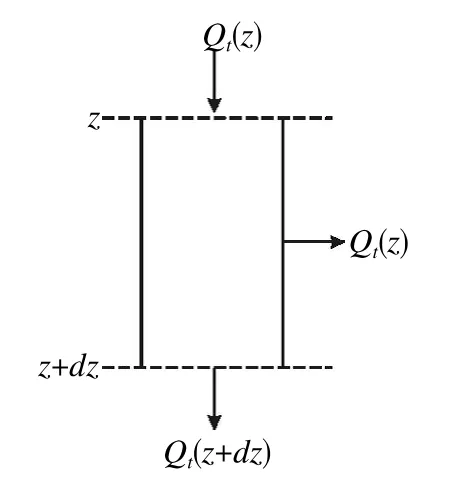
图2 井筒能量守恒微元体分析
流出微元体的热量为:

流入微元体的热量为:
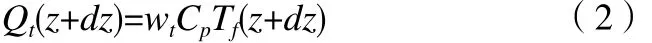
式中,wt为进入微元体的流动流体的质量流量,kg·m-3;Cp为液体的定压比热,J·(kg·℃ )-1;Tf为井筒内流体温度,℃;Qt为井筒周围某点的热量,J。
由于dz很小,可以认为径向的热量损失为从井筒到井筒与地层的交界面之间温差引起的热量传递[6],所以井筒中流体向井筒和地层交界面之间传递的热量为:
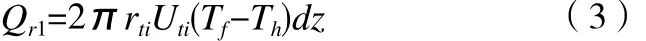
其中,rti为油管内径,m;Uti为以油管内径为起算点的总传热系数,W·m-2;Th为水泥环和地层交界面的温度,℃。
由能量守恒可得:

将式 (1)、(2)、(3)代入式 (4),可得:

从第二接触面(水泥环和地层的交界面)向周围地层传递的热量服从Ramey 无因次时间函数:

井筒向第二接触面传递的热量与第二接触面向周围地层传递的热量相等,故有:

由此可得:
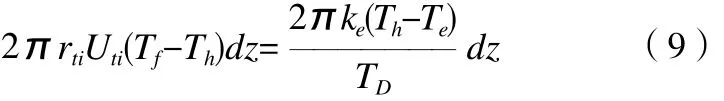
可解得第二接触面温度:


令

周围地层温度根据假设为线性,其表达式为:

式中,g为地温梯度,℃·m-1。
式(12)是一个一元一次非齐次偏微分方程,其解为齐次方程的通解与非齐次方程的特解叠加。将井筒分为许多小段,认为在每一小段内井筒压力为定值,液体定压比热为定值,A为定值。式(12)的解为:

式中,t为生产时间,s;C为待定系数,需要代入边界条件来求取。
由于井套管层次较多,不同深度范围的井筒结构不同,因此需要分段代入不同的边界条件以确定每段的待定系数。各段边界条件可以表示为:

式中:Tfx为第x段井筒入口处流体温度,℃;Tf(x-1)为第x-1段井筒出口处流体温度,℃;zx为井筒分段处与井底距离,m。
根据井筒内一维稳态传热的假设,可以计算井筒内部任意深度和任意半径处的温度:
式中:r为计算点处半径,m;Th为微元处水泥环外边缘温度,℃;Rzro为计算点到水泥环外边缘的热阻,m·℃·W-1;Te为对应井深处的地层温度,℃。
井筒可以简化为由套管、水泥环和环空流体组成的多层组合圆筒体,公式中热阻的计算方法为:

式中:R为热阻,m·℃·W-1;h为对流传热系数,W·(m2·℃)-1;dti为油管内径,m;n为套筒层数,无因次;kj为第j层套筒的导热系数,W·(m2·℃)-1;doj为第j层套筒的外径,m;dij为第j层套筒的内径,m。
2 压裂过程中井筒温度场算例分析
为了验证建立的井筒温度场分析模型的准确性,我们编制了相应的计算程序,利用实际生产数据进行模拟计算,对计算结果进行绘图与分析,最终实现注入过程中井筒温度场的预测。
以某深井压裂施工为例,该井完钻井深6000m,设地层温度梯度为 2.8℃·(100m)-1,年平均地表温度为20℃。在0~1500m油管外径为Φ88.9mm,内径为 74.22 mm;在1500~6000m 其油管外径为Φ88.9mm,内径为76mm。油层套管外径Φ139.7mm,内径为124.3mm。根据地层特点,取参数:岩石热导率为1.75W·(m·℃)-1,地层热扩散率为1.2×10-6m2·s-1。对注入过程中井筒温度场分布进行模拟计算与分析,计算所需参数如表1所示。

表1 油管温度计算参数
2.1 注入时间对井筒温度分布的影响
由于地层温度梯度较高,而注入的液体(水或者压裂液等)温度一般较低,随着注入时间的增加,油管温度会降低。考察了注入排量为4m3·min-1时,注入时间10min、30min以及60min后井筒的温度分布,计算结果如图3所示。注入时间10min、30min以及60min后,6000m井深处的温度分别降低到62℃、50℃及43℃(初始井底温度为140℃)。

图3 注入时间对油管内液体温度的影响
从图3可以看出,随着注入时间增加,井筒温度逐渐降低,其中前10min与30min的温度差距较大,30min与60min的温度差距逐渐减小[7]。这是因为随着井深的增加,地层温度变高,井筒温度也随之升高。注入的液体温度远低于井筒温度,液体受到井筒的加热,温度升高,随着注入时间的增加,井筒与液体之间的热传递逐渐趋于稳定,温度的变化逐渐减小。
2.2 注入排量对井筒温度的影响
注入排量对井筒温度分布具有重要的影响。固定初始温度为20℃,注入时间为1h,考察不同的注入排量时油管内的流体温度分布,计算结果如图4所示。注入排量分别为 2m3·min-1、4m3·min-1及6m3·min-1时,6000m井深处的井筒温度分别从140℃降低到了61℃、43℃及36℃。

图4 注入排量对油管内流体温度分布的影响
从图4可以看出,随着注入排量的增加,井筒温度逐渐降低,并且排量越大,井底温度降低得越严重。因此必须考虑注入流体对管柱的冷却效应,从而考虑温度效应,进行管柱安全评价[8]。
2.3 注入过程对环空温度的影响
对于高温高压井的储层改造过程,由于注入流体温度较低,使得井筒内温度场重新分布,除了油管温度降低以外,还会引起环空内温度降低。环空温度降低会引起套管变形,可能会影响套管安全,造成严重的事故。因此,需要对套管内流体温度进行分析。图5为注入排量分别为2m3·min-1及6m3·min-1时,地层、油管和套管内流体的温度分布。

图5 注入排量对油管和环空内液体温度分布的影响
可以看出,注入排量为2m3·min-1时,油管内温度降低到了61℃,而环空液体温度则降低至69℃。注入排量增加至6m3·min-1时,油管和环空内液体温度则分别降低到了36℃和41℃。在高温环境下,管柱的温度会升高,管柱体积膨胀,水泥环产生的径向应力和切向应力也会增加。随着液体的注入,井筒和环空温度逐渐降低,导致环空压力降低,但若温度降低值过大,环空压力降低较大,套管受到的外挤力将会增加,套管损坏的风险将会增大[9-10]。因此必须考虑注入过程的环空温度降低导致的环空压力降低,避免套管在较高的地层压力下被挤毁,造成安全事故。
3 结论
1)利用能量守恒定律,建立了井筒传热数学模型,并结合计算机技术对实际生产数据进行计算求解,实现了注入过程中井筒温度场的预测。
2)计算结果表明,井筒温度随着注入排量的增大而减小,并且排量越大,井底温度降低得越严重;井筒温度随着流体注入时间的增加而降低,10min与30min的温度差距较大,30min与60min的温度差距逐渐减小。
3)随着流体的注入,井筒内温度将会减小,环空压力将会降低,套管所受的外挤力将会增加,套管的损坏风险也会增加。
[1] 王友启,周梅,聂俊.提高采收率技术的应用状况及发展趋势[J].断块油气田,2010,17(5):628-631.
[2] 李平全.油气田生产开发期套管的损坏原因分析[J].钢管,2006,35(5):53-60.
[3] Hasan A R,Kair C S. Fluid Flow and Heat Transfer inWellbores[M].SPE,Richardson,TX,2002.
[4] 朱德武.凝析气井井筒温度分布计算[J].天然气工业,1998,26(3):28-32.
[5] Ramey H J. Wellbore heat transmission[J].Journal of Petroleum Technology, 1962, 14(4): 427-435.
[6] 卢祥国,赵学猛,袁国英.循环注液过程中井筒温度场的数值计算法[J].石油钻采工艺,1991,8(5):1-4.
[7] 郑杰,张雅蓉,李洁月,等.基于注入与产出过程中的井筒温度场分析[J].石油化工应用,2017,36(5):8-14.
[8] 刘杰,段永刚,何玮,等.高温井井筒温度分布计算方法[J].重庆科技学院学报(自然科学版),2010,12(1):191-193.
[9] 桥智国,叶翠莲.注入井井筒温度分布数学模型的建立与求解[J].天然气技术,2008 (3):30-32.
[10] 窦亮彬,李根生,沈忠厚,等.注CO2井筒温度压力预测模型及影响因素研究[J].石油钻探技术,2013,41(3):76-81.
Calculation of Wellbore Temperature Field and Influence Factors Analysis during Fluid Injection
CHEN Chaofeng1,WANG Buxin1,FU Qianjin2,LI Xuebin1,HU Guangwen1,LIU Ao3
(1.Exploration Utility Department of Xinjiang Oilfield Company, Petro China, Karamay 834000, China; 2. Downhole Service Company, XDCE, CNPC, Karamay 834000, China; 3. College of Petroleum Engineering, Yangtze University, Wuhan 430100, China)
In the fracturing and acidification during the implantation process, if wellbore temperaturefield was changed, it would not only caused the performance of fluid injection, but also underground pipe and casing would influenced by the temperature effect and resulting in deformation of pipe string. Based on the law of conservation of energy, the wellbore heat transfer mathematical model was established,combined with the computer technology, the actual production data was calculated. The injection wellbore temperaturefield in the process was predicted, a theoretical basis for the reasonable selection of injection operation parameters was provided.
wellbore; temperaturefield; temperature; heat transfer
TE 357
A
1671-9905(2017)11-0055-04
陈超峰(1971-),男,高级工程师
刘奥(1991-),男,长江大学石油工程在读硕士研究生,研究方向:岩石力学及钻采工艺技术研究。E-mail:454669722@qq.com
2017-07-24
