新的基于身份认证的群密钥协商协议

陈海红，李军义

1.湖南永州职业技术学院 计算机系，湖南 永州 425000 2.湖南大学 信息科学与工程学院，长沙 410082

新的基于身份认证的群密钥协商协议

陈海红1，李军义2

1.湖南永州职业技术学院 计算机系，湖南 永州 425000 2.湖南大学 信息科学与工程学院，长沙 410082

群密钥协商（GKA）协议在构建安全多播信道中扮演着主要角色。由于公钥管理的简洁性和高效性，基于身份的认证群密钥协商协议密码系统近年来成为热门研究方向。提出了一个基于Weil对和完全三叉树结构的群密钥协商协议，同时提出了成员加入和离开子协议。对新方案的安全性进行了分析，结果显示，新方案可以抵抗常见的攻击。在性能方面，新方案在参与者较多时有较明显的计算优势。

群密钥协商；基于身份的认证；Weil对；三叉树

1 引言

密钥建立协议可以帮助一组参与者通过公开、不安全的网络交换信息来生成一个会话密钥。该密钥能够用来实现参与者的安全目标，例如认证、保密和数据完整。生成会话密钥的方法有两种：密钥分发和密钥协商。密钥分发需要一个群控制者来持有群组中所有参与者的信息。如果群控制者被攻击，那么群组密钥生成即告失败。该方法的优势在于：由于群成员可以随时加入或者离开群组，群控制者在这种情况下有明显的存在价值。相反的，密钥协商不需要群控制者，群中的所有参与者通过密钥协商生成会话密钥。由于会话密钥包含了所有参与者的信息，因此任何一个参与者都无法控制或者预测会话密钥。

第一个密钥协商协议是由Diffie与Hellman在文献[1]中提出的。Diffie-Hellman协议能够保证两个参与者之间的通信安全。但是没有对参与者身份进行认证，因此容易遭到“中间人攻击”。1986年，Matsumoto、Takahima和Imai[2]扩展了Diffie-Hellman协议，提出了三个双方认证密钥协商协议：MTI/A0、MTI/B0和MTI/C0。这些协议能够通过巧妙的消息传递而不需要签名，为通信双方产生能够抵抗被动攻击者攻击的双向认证的会话密钥。Joux[3]利用Weil对实现了三方的密钥协商协议。当有三个参与者想要协商一个公共的会话密钥时，协议中每个参与者只需要传送一条消息。但是，Joux提出的协议也无法认证参与者，而且同样容易遭到“中间人攻击”。

以上两种密钥协商技术都能够重复步骤为动态的群组建立会话密钥。然而，如果群成员较多或者协议的通信代价非常昂贵，上述方法的效率则会降低。因此，许多动态群密钥协商协议为增加和离开的群成员而设计高效的操作[4-6]。例如，Sherman在文献[7]中首次提出了将单向的函数树（OFTs）用来计算密钥树。在该方案中，密钥是从叶子节点到根节点来进行计算的。另外，满足一些特殊性质的任意两个参与方的密钥协商协议都能够通过使用单向函数树扩展成为n个参与方的密钥协商协议。

Reddy和Nalla[8]利用单向函数树设计了首个基于身份的群密钥协商协议，同时将两方认证的密钥协商协议扩展为可认证的群密钥协商协议。Shiau等人[9]的协议同样使用密钥树结构。但是该方案使用完全二叉树结构，也就是说树中的每一个节点代表一个参与者。Barua等人[10]将Joux等人[3]提出的基础协议成为多方协议。在他们的协议中树的叶子节点表示个体参与者并且每一个内部节点分别与以该节点为根节点的子树相对应的参与者集合匹配。但是该协议同样没有认证。Dutta等人在文献[11]中利用多方签名实现了该协议的认证性。

本文提出了一种新的基于Weil对的群密钥协商协议。本协议利用基于身份的认证和完全三叉树结构，使得树中的每一个节点代表群中的一个参与者。如果一些参与者想要加入或者离开群，不需要群中的所有参与者重新更新他们的计算来获取密钥，因此这适合于动态变化的环境。

本文组织如下：第2章介绍一些概念和假设。第3章提出新协议。随后的两章进行安全性分析和性能分析。最后一章为本文结论。

2 准备知识

假设G1是一个阶为素数q的加法群，G2是一个阶为素数q的乘法群。P是G1的生成元。假设离散对数问题（DLP）在群G1和G2中是难解的。e是两个群上的双线性映射e:G1×G1→G2，这一双线性映射满足下面的性质。

（1）双线性：对于所有 P,Q∈G1和 a,b∈Z*q，有e(aP,bQ)=e(P,Q)ab成立。

（2）非退化性：如果 P是 G1的生成元，那么e(P,P)≠1。

（3）可计算性：存在有效的算法计算e(P,Q)，其中P,Q∈G1。

为了使用双线性映射来实现协议，给出以下问题和假设[12]：

（1）G1中的HDH（Hash Decisional Diffie-Hellman）问题：给定(P,aP,bP,c)和哈希函数 H1:G1→Z*q，判定等式c=H1(abP)modq是否成立。

HDH假设：不存在多项式时间算法解决G1中的HDH问题。

（2）BDH（Bilinear Diffie-Hellman）问题：给定(P,aP,bP,cP)，计算 e(P,P)abc。

BDH假设：不存在多项式时间算法解决BDH问题。

（3）DHBDH（Decisional Hash Bilinear Diffie-Hellman）问题：给定(P,aP,bP,cP,d)和一个哈希函数 H2:G2→Z*q，判定等式d=H2(e(P,P)abc)modq是否成立。

DHBDH假设：不存在多项式时间算法解决DHBDH问题。

3 提出的协议

新协议分为三个阶段：初始化阶段、密钥协商阶段和成员变更阶段。为了实现基于身份的认证，初始化阶段时每名参与者需要在KGC（Key Generation Center，密钥生成中心）中注册。

3.1 初始化阶段

本小节描述每个参与者如何在KGC中注册。在KGC中注册结束后每名成员能够执行下一阶段来计算群会话密钥。为了达到这个目的，首先由KGC选择随机数 s∈RZ*q，然后计算并公开 Ppub=sP作为公钥。KGC秘密的保存s作为其主密钥。每名参与者的身份和其长期公钥分别是IDi∈{0,1}*和Qi=H(IDi)。每一个参与者将会使用Qi通过安全信道在KGC中进行注册：

步骤1参与者Ui发送Qi给KGC。

步骤2 KGC计算参与者Ui的长期私钥Si=sQi，并将Si发送给Ui。

协议的公共参数为：(G1,G2,e,q,P,Ppub,H,H1,H2,H3)，其中H3:G1×G1→Z*q是安全Hash函数。

3.2 密钥协商阶段

本小节定义被授权的参与者如何共同合作来计算公共的会话密钥。本协议中密钥协商过程保留了基于完全三叉树的结构。树中的每一个节点都代表一个参与者，如图1所示的例子中有16个参与者。

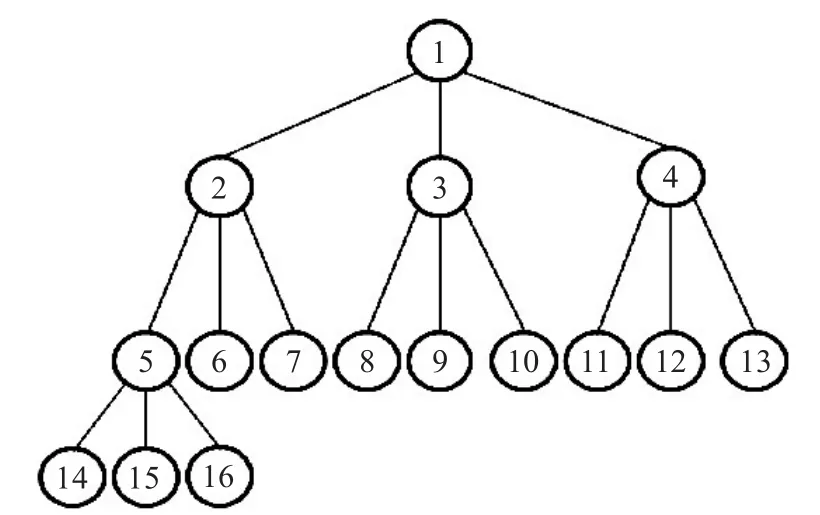
图1 由16个参与者组成的群表示的一个完全三叉树

假设一个群中有n名参与者，每一名参与者Ui(i∈{1,2,…,n})都有他们自己的长期公钥/私钥(Qi/Si)。在每一轮新的协议中，参与者将会选择随机数ai作为临时私钥。在完全三叉树中有四类节点：叶子节点，只有一个左子节点的内部节点，有两个子节点（男孩和女孩）的内部节点以及第四类节点是有三个子节点的内部节点。

类型1节点为叶子节点(3i＞n)。

1.1 令ti=ai。

1.2 参与者Ui发送ti⋅P给他的（她的）父节点以及他的（她的）兄妹节点（兄弟或者姐妹）。

类型2节点只有一个子节点(3i-l=n)。

2.2 参与者Ui发送消息(Pi,,Ti)给参与者U3i-1，其 中 Pi=aiP,以 及 Ti=H3(Pi,+aiPpub。参与者U3i-1发送消息(P3i-1,T3i-1)给参与者Ui，其中P3i-1=a3i-1P以及T3i-1=H1(P3i-1)S3i-1+a3i-1Ppub。

2.3 参与者Ui验证下面的等式e(T3i-1,P)=e(H1(P3i-1)Q3i-1+P3i-1,Ppub)并且参与者U3i-1验证下面的等式 e(Ti,P)=e(H3(Pi,+Pi,Ppub)。

2.4 如果2.3中的等式成立，那么Ui计算 Ki=e(P3i-1,并且 U3i-1计算 K3i-1=e(Pi,。注意K3i-1=e(P,P)=Ki。

2.5 如果i=1，那么会话密钥就是Ki，否则参与者Ui设置ti=H2(Ki)并发送Pi=tiP给他的父节点、兄妹节点和群中兄妹节点的子节点。

类型3该节点有两个子节点(3i=n)。这种情况下，三个参与者Ui、U3i和U3i-1简单地执行三方一轮的密钥交换。

3.1 参与者Ui发送消息(Pi,Ti)给参与者U3i和U3i-1。参与者U3i-1发送消息(P3i-1,T3i-1)给参与者Ui和U3i。最后，参与者U3i发送消息给参与者Ui和U3i-1，其中一般的Pk=akP并且Tk=H1(Pk)Sk+akPpub,(k=i,3i-1,3i)。

3.2 这一步骤中一般的每一个参与者Uk验证从其他两个参与者那里收到的消息(PA,TA),(PB,TB)是否满足下面的等式：e(TA+TB,P)=e(H1(PA)QA+H1(PB)QB+PA+PB,Ppub)。

3.3 如果步骤3.2中的等式成立，那么：

（1）Ui计算 Ki=e(P3i,P3i-1)ai=e(P,P)aia3ia3i-1。

（2）U3i-1计算 K3i-1=e(P3i,Pi)a3i-1=e(P,P)aia3ia3i-1。

（3）U3i计算 K3i=e(Pi,P3i-1)a3i=e(P,P)aia3ia3i-1。

显然Ki=K3i=K3i-1。

3.4 如果i=1，那么会话密钥是Ki，否则参与者Ui设置ti=H2(Ki)并发送Pi=tiP给他的父亲节点、兄妹节点和群中的兄妹的子节点。

类型4该节点有三个子节点。

之前解释过的类型（类型1、类型2和类型3）都类似于Hwang等人提出协议中的完全三叉树类型（本文中使用不同的等式用来认证，该认证需要两个对，然而他们的认证需要三个对）。

这一类型是本文的主要贡献之一，完全三叉树的密钥协商阶段重要部分描述如下：

4.1 每一个参与者选择ak∈RZq*然后计算Pk=akP和T=H1(Pk)S+aPpub。

（1）Ui发送消息 (Pi,Ti)给参与者 U3i-1,U3i和U3i+1。

（2）U3i-1发送消息(P3i-1,T3i-1)给参与者Ui,U3i和U3i+1。

（3）U3i发送消息 (P3i,T3i)给参与者Ui,U3i-1和U3i+1。

（4）U3i+1发送消息(P3i+1,T3i+1)给参与者Ui,U3i和U3i-1。

4.2 每一个参与者验证前一步骤中收到的消息。

（1）一般的，参与者Uk通过下面的等式验证收到的消息(PA,TA),(PB,TB),(PC,TC)：

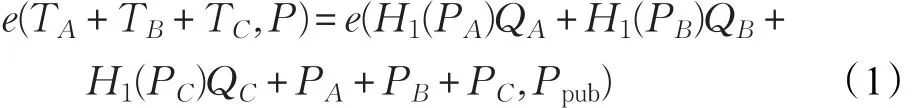
（2）注意每一个参与者都要同时验证其他三个参与者。

4.3 如果对于参与者Ui和U3i关系式（1）验证成立，那么

（1）Ui分别计算并发送消息(Pi,3i+1,),(Pi,3i-1,和 (Pi,3i-1,给参与者 U3i-1,U3i和U3i+1。

（2）U3i同样计算并发送消息 (P3i,3i-1,给参与者Ui。

（3）一般的，Pi,j=aiPj以及=H1(Pi,j)Si+aiPpub。

4.4 一般的，每一个参与者Uk通过下面的等式验证收到的消息 (Pi,j,：

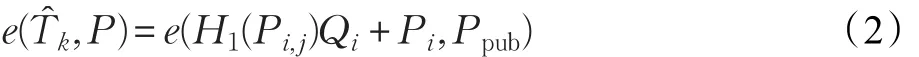
4.5 最后，如果等式（2）成立，每一个参与者计算如下密钥：

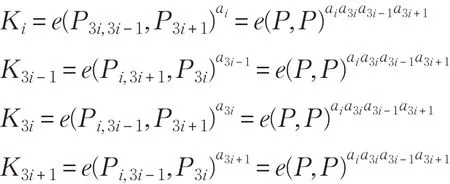
很明显，所有计算的密钥全部相等，也就是说Ki=K3i=K3i-1=K3i+1。

4.6 如果i=1也就是说参与者抵达了树的根节点并且会话密钥为 Ki，否则Ui设置ti=H2(Ki)并发送Pi=tiP给群中他的父节点，兄妹节点以及兄妹节点的子节点。

每一名参与者执行以上过程，直到抵达根节点，因此群中的所有参与者可以获得公共的会话密钥Ki。

3.3 成员变化节点

通信过程中参与者可能想要加入或者离开群组都是有可能的。为了安全考虑，那些在加入群之前和离开群之后的参与者必须不能获取群中发送的消息。因此，必须为那些想要加入或者离开群组的参与者执行一些操作。

3.3.1 加入子协议

假设在任意参与者加入群组之前群中有n个参与者。新来的参与者在完全三叉树中被安放在第n+1个节点的位置。为了加入群组，该参与者将执行下面的步骤：

（1）参与者U1将包含了群参与者数目和所有参与者公钥的群组信息发送给第n+1个参与者。

（2）参与者Un+1选择随机数an+1∈RZ*q作为临时的私钥，然后计算并广播Pn+1=an+1P和签名Tn+1=H1(Pn+1)an+1+an+1Ppub。

当参与者Un+1加入到有n个参与者的群组中时，在原始的群组中，参与者的数量有三种可能的模式。

模式1n=0mod3或者n=3K。

这时，在参与者Un+1加入群组后最后一个父节点有三个子节点，见图2。

图2 新增的第16个参与者

令i=n/3，Ui是新来参与者Un+1的父节点。在这种类型中Ui具有三个子节点并且会话密钥的计算过程类似于类型4中的密钥协商节点。这种情况下，Un+1扮演类型4中U3i+1的角色。在类型4的最后：

Ui计算 Ki=e(P3i,3i-1,Pn+1)ai。

U3i-1计算 K3i-1=e(Pi,n+1,P3i)a3i-1。

U3i计算 K3i=e(Pi,3i-1,Pn+1)a3i。

Un+1计算Kn+1=e(Pi,3i-1,P3i)an+1。

显然，Ki=K3i=K3i-1=Kn+1=e(P,P)aia3ia3i-1an+1。如果i=1，那么会话密钥就是Ki，否则Ui设置ti=H2(ki)并广播Pi=tiP给群中他的父节点，兄妹节点和兄妹节点的子节点。然后他继续执行密钥协商节点直到抵达根节点。

模式2n=1mod3或者n=3k+1

在参与者Un+1加入群组之后，最后一个父节点只有一个子节点（见图3）。令i=(n+2)/3，那么Ui是新来参与者Un+1的父亲节点，此时Ui只有Un+1作为他的子节点。与类型2中的密钥协商节点类似。

图3 新增的第14个参与者

（1）参与者Ui选择另外一个额外的随机数并计算 Pi=aiP,和 Ti=H3(Pi,+aiPpub，然后发送消息 (Pi,Ti)给参与者Un+1。

（2）参与者Un+1同样计算 Pn+1=an+1P和Tn+1=H1(Pn+1)Sn+1+an+1Ppub，然后发送消息(Pn+1,Tn+1)给参与者Ui。

（3）与类型2中的步骤2.3一样，Ui和Un+1同时验证他们收到的消息。如果验证成功，那么Ui计算Ki=e(Pn+1,以及 Un+1计算 Kn+1=e(Pi,。注意 Kn+1=e(P,=Ki。

如果i=1那么会话密钥就是Ki，否则参与者Ui设置ti=H2(Ki)并发送Pi=tiP给群中他的父节点，兄妹节点和兄妹节点的子节点，然后继续密钥协商阶段直到抵达根节点。

模式3n=2mod3或者n=3K-1

这就表示当参与者Un+1加入群组之后，三叉树的最后一个父节点有两个子节点（见图4）。

图4 新增的第15个参与者

令i=(n+1)/3，Ui是新来参与者Un+1的父亲节点。这种类型下Ui有两个子节点，其计算会话密钥的过程就与类型3中密钥协商过程类似，在执行步骤3.1和3.2之后：

Ui计算 Ki=e(Pn+1,P3i-1)ai=e(P,P)aian+1a3i-1。

U3i-1计算 K3i-1=e(Pn+1,Pi)a3i-1=e(P,P)aian+1a3i-1。

Un+1计算 Kn+1=e(Pi,P3i-1)an+1=e(P,P)aian+1a3i-1。

显然，Ki=Kn+1=K3i-1。如果i=1，那么会话密钥就是 Ki，否则Ui设置ti=H2(Ki)并发送 Pi=tiP给他在群中其他的父节点、兄妹节点和兄妹节点的子节点。随后继续进行密钥协商，直到抵达根节点。

为了更新会话密钥，在从第n+1个节点到第一个（根）节点的路径上的每一个节点所保存的每一个会话密钥Ki都会被改变。至此，加入协议的所有三种类型都已介绍，会话密钥K5,K2和后续的K1都会被改变。图5显示了当参与者U16加入群组后这些改变的路径。

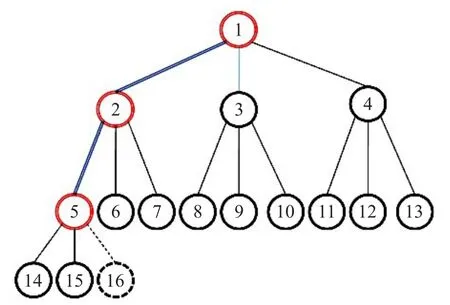
图5 U16加入后 K5，K2和 K1值将被改变

3.3.2 离开子协议

假设原来群组中有n个参与者，令离开的参与者为Ul，那么更换Un和Ul的位置，随后删除参与者Ul并更新会话密钥。根据Ul的位置，有如下三种模式。

模式1l=n

这种模式中，离开的参与者是三叉树的最后一个节点。协议可以直接删除最后一个节点Un，然后生成一个新的公共会话密钥。

（1）如果n=3k+1，令i=(n+2)/3。这种类型中，当Un离开群组后，Ui拥有两个子节点。Ui选择一个新的随机数作为临时秘密密钥并执行类型3中密钥协商阶段的相同操作。

① Ui计算和，然后发送消息给参与者 U3i-1和 U3i，最后计算 Ki=

② U3i-1验证完消息后计算 K3i-1=e(P3i,

③ U3i同样验证消息后计算 K3i=e(P3i-1,

④如果i=1，那么会话密钥就是Ki，否则Ui设置ti=H2(Ki)并发送Pi=tiP给群中他的父节点、兄妹节点和兄妹节点的子节点，然后继续执行密钥协商阶段直到抵达根节点。

（2）如果n=3K，令i=n/3。在这种类型中当Un离开群组后，Ui只有一个子节点，并与类型2中的密钥协商阶段一样重新选择另外一个额外的随机数。

① Ui计 算和aiPpub并发送消息给参与者U3n-1。

②U3n-1同样发送消息(P3n-1,T3n-1)给参与者Ui，其中P3n-1=a3n-1P以及T3n-1=H1(P3n-1)S3n-1+a3n-1Ppub。

③Ui和U3n-1像类型2中的步骤2.3一样验证他们收到的消息。如果验证关系成立，那么Ui计算Ki=计 算其中

④如果i=1，那么会话密钥就是Ki，否则Ui设置ti=H2(Ki)并发送Pi=tiP给群中他的父亲节点、兄妹节点和兄妹节点的子节点，然后继续执行密钥协商阶段直到抵达根节点。

（3）如果n=3k-1，令i=(n+1)/3。这种类型中当参与者Un离开群组后，Ui没有任何子节点，因此他选择一个新的随机数作为他的临时密钥并以替换ti，然后发送和最后 Ui更新Ki并随后继续密钥协商阶段直到抵达根节点。

模式2l=1

该模式离开参与者的位置是在三叉树的根节点。因此，协议删除根节点U1并用最后的一个节点Un替代，然后执行已经解释过的模式1中的离开子协议以生成一个新的公共密钥。图6显示了一个原先有16个参与者的群组中U1离开群的例子。

图6 节点16代替第1个离开节点

模式3l∈{2,3,…,n-1}

该模式中协议用Un（三叉树中的最后一个节点）替换Ul，并继续模式1中的离开子协议来生成一个新的公共会话密钥。

4 安全性分析

新协议可以抵抗未知密钥共享攻击、密钥泄露伪装攻击和密钥控制攻击，还具有可认证性和前向安全性。本章将重点分析这些安全属性。

（1）未知密钥安全性

未知密钥安全是指如果一个会话密钥已经被泄露，那么当前协议的运行不应该受到安全影响。假设群中有四个参与者U1,U2,U3和U4，而之前的会话密钥是

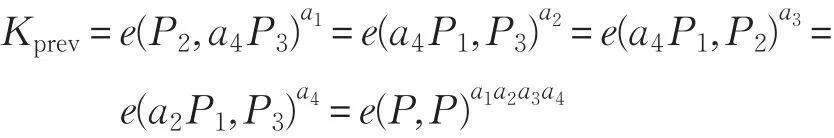
如果攻击者想要提取指定的临时密钥（例如a1），那么他（她）必须解决G2中的BDHP问题，而该问题却是难解的。同样，会话密钥取决于密钥协商中每次运行参与者所选择的随机数，所以会话密钥每次都是不同的。

（2）身份认证性

（隐式的）密钥认证需要每个合法的协议参与者必须确保除了合法参与者之外没有其他成员能够建立群会话密钥。在协议中，每个参与者利用他的/她的长期密钥对生成消息进行签名，因此所有参与者一旦收到从其他人那里的消息，首先验证消息，然后执行协议步骤。因此参与者当前只能被合法的参与者执行并建立群会话密钥。

（3）前向安全性

前向安全是指如果参与者的长期密钥被泄露，那么之前会话密钥的安全性不应该受到影响。在提出的协议中，长期密钥只用作认证，协议并不使用参与者的长期密钥计算公共的会话密钥。因此很明显本文协议满足前向安全性。

（4）密钥泄露伪装攻击的抵抗性

该安全性质防止攻击者获取某参与者的长期密钥后伪装成为其他参与者。长期密钥通常是被用来签名或者解密的密钥，所以长期密钥主要被用来认证的目的，而不是实际的群密钥计算。因此不需要考虑该安全攻击。

（5）密钥控制

密钥控制是指群中的任何合法参与者都不能决定或者影响会话密钥的值。本文协议中公共的会话密钥取决于群中所有参与者的合作，因此没有人能控制或者预先决定会话密钥。

5 性能分析

除了安全性，协议的效率也是影响协议能否面向工业应用的一个重要衡量指标。从协议的轮数、传递信息的总数和对运算的总数三个方面对协议性能进行分析。

由于文献[8]和文献[11]都使用了密钥树结构。由于文献[11]中提出的协议中每一个参与者都代表叶子节点，同样他/她也需要持有从叶子节点到根节点的秘密值。文献[11]使用三叉树结构而文献[8]使用了完全二叉树结构，树中的每一个节点代表一个参与者。新协议使用了完全三叉树结构，同样树中的每一个节点代表一个参与者。相反，与文献[11]中的协议相比，新协议是基于参与者的身份，因此本章不讨论PKI使用代价。

为了计算全部对运算的数量，将所有叶子节点上的对运算和内部节点上的对运算的个数相加。为了计算会话密钥，叶子节点将会继续执行3.2节中（根据其类型）说明的计算步骤直到抵达树的根节点。因此，树的叶子节点代表的参与者应该重复计算R(n)次，其中R(n)表示协议执行的轮数，并且叶子节点上面有个叶子，但是应该注意会有不在最后一层上面的叶子节点（例如 R(n)），并且他们可能会在[R(n)-1]层，因此他们会重复比R(n)层上的叶子节点少一轮的计算。那么应该从中减去他们的数量，并且可以检查最后一层上有个叶子节点。对于内部节点，在每一层l上面，有3l个参与者。他们中的每一个都要重复l+1次3.2节中说明的步骤直到获得会话密钥，因此从第0层到第R(n)-1层共计最后3.2节中说明的步骤共需要重复执行次，并且为了获得步骤3.2中的公共密钥Ki，需要4个对预算来认证消息以及一次对运算计算Ki。因此应该将上面的式子乘以5。显然，当参与者数量较多时，新方案的计算优势比较明显。

为了计算参与者传送的消息数量总数，每个内部节点都会发送9个消息，每个叶子节点都会发送4个消息，分别通过内部节点的总数9与叶子节点的总数4相乘，再分别把他们相加，能够发现B(n)最多≤5(n-1)。本文协议比文献[11]的协议在通信消耗上面更有优势。

表1对文献[8]、文献[11]和本文方案进行了详细对比，如上述分析，新方案在参与者较多时有比较明显的计算优势。

6 小结

本文提出一种利用对运算实现的基于身份的认证群密钥协商协议。在本协议中，每一名参与者能够通过基于身份的认证结构验证收到的消息。协议不需要验证参与者的公钥证书。还研究了参与者如何进入或者离开群组。这表明本文协议适合存在成员变化的组织。

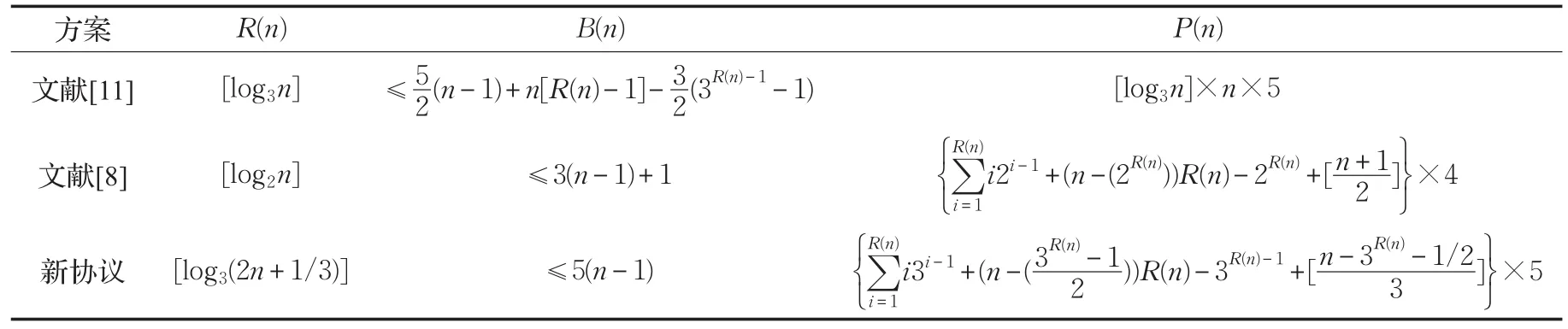
表1 计算和通信负担对比

[1]Diffie W，Hellman M E.New directions in cryptography[J].IEEE Transactions on Information Theory，1976，22（6）：644-654.

[2]Matsumoto T，Takashima Y，Imai H.On seeking smart public-key-distribution systems[J].The Transactions of the IEICE，1986，69（2）：99-106.

[3]Joux A.A one round protocol for tripartite Diffie-Hellman[J].Journal of Cryptology，2004，17（4）：263-276.

[4]李明.新的适用于WSN网络的双方认证密钥协商协议[J].计算机工程与应用，2016，52（3）：100-102.

[5]钱琦锋，程春玲.WSN中基于非双线性对的无证书群组密钥协商协议[J].计算机科学，2015，35（7）：186-190.

[6]袁思敏，马传贵，相生奇.非平衡网络环境下基于身份的组密钥交换协议[J].计算机科学，2015，35（5）：1399-1405.

[7]Sherman A T，Mcgrew D A.Key establishment in large dynamic groups using one-way function trees[J].IEEE Transactions on Software Engineering，2003，29（5）：444-458.

[8]Reddy K C，Nalla D.Identity based authenticated group key agreement protocol[C]//International Conference on Cryptology：Progress in Cryptology，2002：215-233.

[9]Shiau S H，Hwang R J，Lin M F.Key agreement protocol based on Weil pairing[C]//International Conference on Advanced Information Networking and Applications，2005，1：597-602.

[10]Barua R，Dutta R，Sarkar P.Extending Joux’s protocol to multi party key agreement（Extended Abstract）[J].Lecture Notes in Computer Science，2003：205-217.

[11]Dutta R，Barua R，Sarkar P.Provably secure authenticated tree based group key agreement[J].Lecture Notes in Computer Science，2004，3269：92-104.

[12]陈虹，郑艳艳，肖振久.无双线性对无证书两方跨域认证密钥协商协议[J].计算机工程与应用，2015，51（7）：74-79.

CHEN Haihong1,LI Junyi2

1.Department of Computer,Yongzhou Vocational Technology College,Yongzhou,Hunan 425000,China 2.College of Computer Science and Electronic Engineering,Hunan University,Changshan 410082,China

Novel ID-based group authenticated key agreement scheme.Computer Engineering and Applications,2017,53（21）：103-109.

Group Key Agreement（GKA）protocol plays a key role in the construction of secure multicast channels.Because of the simplicity and efficiency of public key management,the ID-based Authenticated Group Key Agreement Protocol（AGKA）cryptosystem has become a hot research direction in recent years.This paper proposes a new Weil pairing and completely trigeminal tree based group key agreement protocol,designs the participants join-and-leave pre-protocol.Security analysis and performance analysis show that the new scheme satisfies all known security requirements.Compared with the existing schemes,the new scheme has obvious advantages in terms of performance.

Group Key Agreement（GKA）;ID-based authentication;Weil pairing;trigeminal tree

A

TP309

10.3778/j.issn.1002-8331.1605-0280

湖南省教育厅课题项目（No.13C971）。

陈海红（1982—），女，讲师，主要研究领域为多媒体制作，安全协议设计，RFID安全；李军义（1970—），男，博士，副教授，研究方向：软件工程，信息安全。

2016-05-19

2016-08-24

1002-8331（2017）21-0103-07

CNKI网络优先出版：2017-02-10,http://www.cnki.net/kcms/detail/11.2127.TP.20170210.0810.014.html