火星全球遥感探测器多学科建模与协同优化

柳明星 张恒 张伟



火星全球遥感探测器多学科建模与协同优化

柳明星 张恒 张伟

（上海卫星工程研究所，上海 201109）

针对火星全球遥感探测器的总体参数设计与优化问题，基于多学科设计优化（Multidisciplinary Design Optimization，MDO）的思想，首先建立以遥感性能和总质量为综合优化目标的总体优化模型，从而实现对总体指标的分解，作为分系统设计的输入条件。基于总体指标分解的结果，然后对探测器的载荷、电源和控制等分系统的变量及约束进行分析，得到分系统优化模型。采用协同优化方法对整个优化问题的耦合关系进行协调并由总体向分系统传递指标和相关耦合参数，采用自适应动态罚函数法和多种优化算法协作优化的寻优机制，来提高总体优化与分系统优化寻优收敛的速度，从而求解获得协同一致的探测器总体参数优化结果与分系统优化结果，验证了MDO方法应用于航天器总体设计的有效性。

建模 罚函数 协同优化 多学科设计优化 火星探测器

0 引言

航天器的设计是一个多学科交叉、权衡和优化的过程[1]。涉及结构、电源、热控、姿态与轨道控制、测控数传等多个分系统。随着航天器功能的不断提高以及现代航天器设计对研制周期等的更高要求，对数字化总体设计技术的需求越来越迫切，数字化总体设计技术将成为航天器设计的发展趋势。

传统航天器设计模式是一种以“经验型”为主的串行迭代设计模式，通过总体与分系统间反复人工协调、迭代，最终得到系统可行解而非优化解，但未能充分利用各分系统间的相互耦合的影响，因而降低了航天器整体性能。

多学科优化设计作为一种考虑多学科耦合关系，旨在解决复杂系统优化问题的方法，则提供了一种有助于提高数字化设计水平的思路与途径。近年来，国内外学者在航天器MDO（Multidisciplinary Design Optimization，MDO）领域取得了一定成果，文献[2]基于协同优化（Collaborative Optimization, CO）的思想，提出了采用分布式设计架构来设计大型复杂系统的方法；文献[3-4]则将MDO方法应用到小卫星的参数优化设计中，大大提升了设计效率；文献[5]对月球基地的多学科优化进行了研究，旨在寻找优良的基地材料组成，对其优化所涉及的热、结构、空间辐射、材料属性等学科进行了分析，采用遗传算法实现了月球基地的优化；文献[6-7]提出了一种非嵌套的协同优化方法（Nonnested Collaborative Optimization, NNCO），并将其应用到遥感卫星的总体参数优化中，相比于传统协同优化方法，其优化效率更高。

火星探测是当今深空探测研究的热点[8-10]。本文以火星全球遥感探测器为研究对象，建立以遥感性能和总质量为综合优化目标的MDO模型，在协同优化框架下，基于罚函数法以及多种优化算法协作优化的寻优机制进行求解，以提高探测器总体设计的整体性能。

1 优化问题建模

1.1 总体优化模型

（1）优化目标

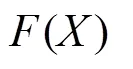
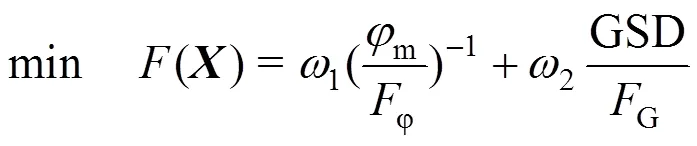
（2）约束条件

探测器为了满足成像要求，中分相机火表像元分辨率GSD和载荷幅宽应满足一定要求，本文假设分辨率优于80m，幅宽不小于240km，故需满足式（2）

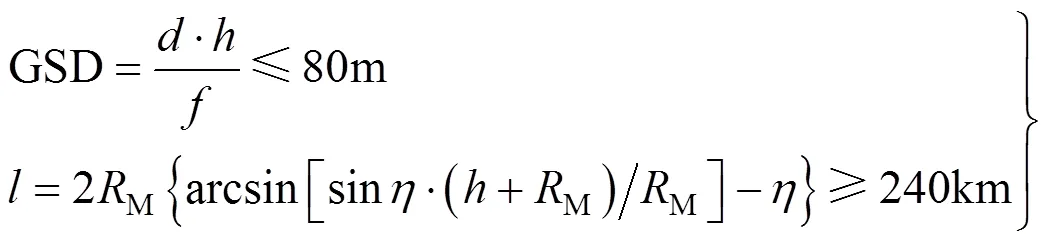
式中为相机像元尺寸；为相机焦距；为探测器离火星表面的高度；M为火星半径；为相机视场半张角。

探测器在近火弧段执行成像观测时，每一幅图观测长度为一个幅宽，要求任意相邻两图具有一定的重叠观测区域，这里假设重叠区域不小于2%。为保证相机载荷相邻两图之间不出现间隙，需保证姿态指向精度j满足式（3）

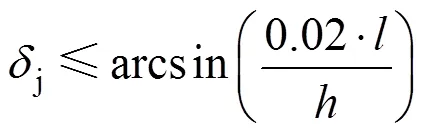
对于稳定度，一般来说，卫星本体在飞行中抖动对图像影响应有一定限制。对于近火弧段轨道高度在时，载荷像元对应地面分辨率GSD时，规定抖动应小于一个像元的20%，则稳定度w需满足式（4）

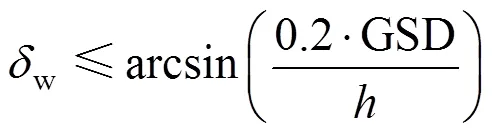
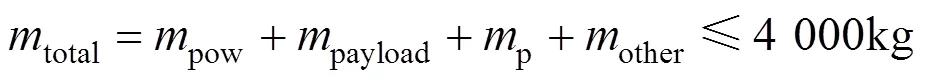
（3）总体优化模型

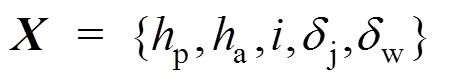
1.2 分系统模型

（1）载荷分系统

探测器的有效载荷为一台中分辨率相机，有效载荷分系统的输入条件为探测器的轨道条件，CCD相机的焦距和像元尺寸，输出为相机功耗、传函、质量等。

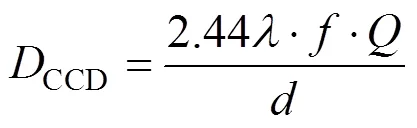
式中为CCD相机焦距；为一个像元尺寸大小；为波长；为成像参数，一般在0.5~2.0之间，这里假设=1.1。

对于一个圆孔径没有遮拦的光学载荷系统，调制传递函数MTF理论计算公式如式（7）[12]

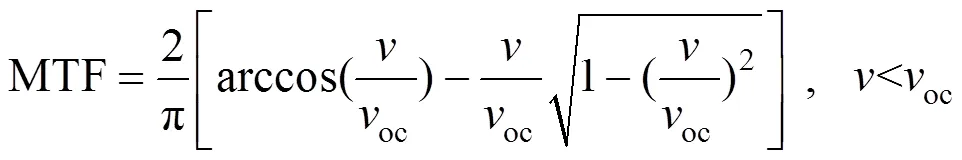
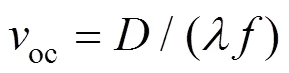
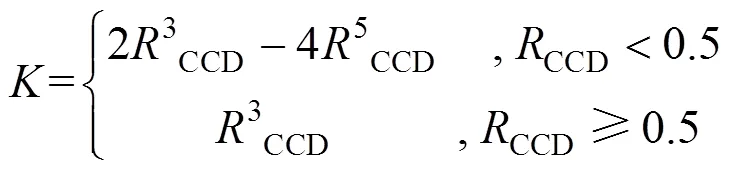
（2）电源分系统

电源分系统负责为探测器提供电能，是航天器重要的服务系统之一。电源分系统分为太阳电池阵和蓄电池两部分。

考虑太阳翼功率输出最紧张的情况，即太阳电池阵工作在寿命末期，其最大输出功率sa为[13]

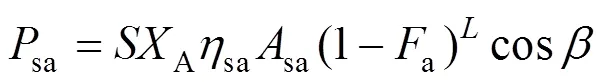
表1 不同太阳电池材料的性能参数

Tab.1 Performance parameters for different solar cell materials

探测器环火任务期间会出现火影，火影期太阳电池的功率输出为0，探测器的整个功耗靠蓄电池放电来支持。出火影后，一方面，太阳电池要维持探测器的功耗需求，另一方面，太阳电池的剩余功率对蓄电池进行充电。

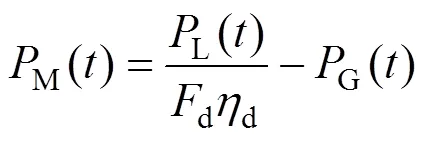
若负载小于太阳电池的供电能力，则太阳帆的剩余功率可对蓄电池进行充电。充电功率为

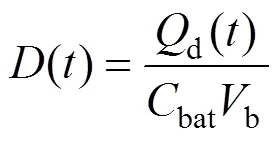
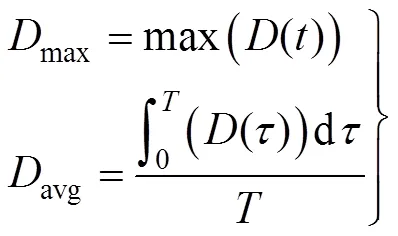
式中为轨道周期，包括火影时间、充电时间以及近火弧段实施遥感的时间。

电源分系统的质量由太阳翼质量、蓄电池质量以及电源控制器质量组成。太阳翼的质量sa可近似表示为

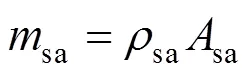
蓄电池质量bat可以根据蓄电池的比能量进行估算，即

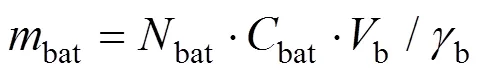
电源控制器为电路部件，其质量模型难以建立，因此本文参考现有工程产品，对其取常值20kg。

综上，电源分系统的质量为

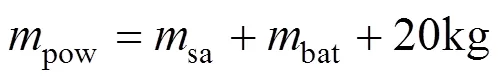
（3）控制分系统

控制分系统设计的目标是根据总体优化分解的指向精度和稳定度要求，结合控制分系统测量装置、执行机构等约束，基于航天器姿态动力学理论，设计出满足环绕器在环火任务期间对火定向遥感的控制规律。

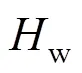
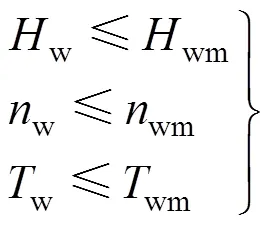
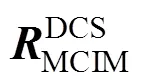
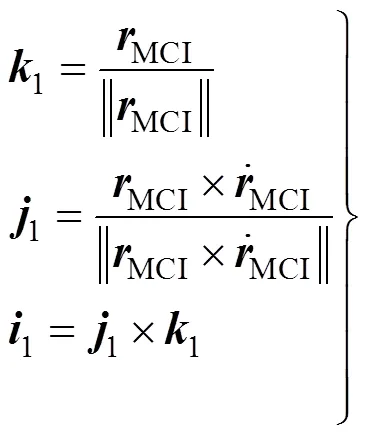
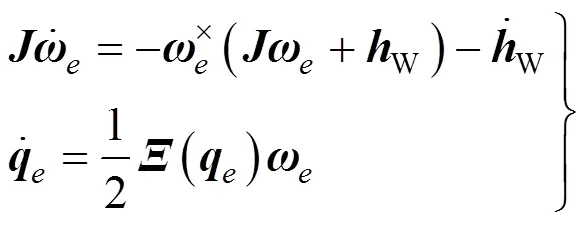
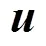
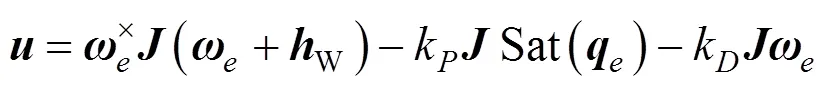
综上，控制学科的分析模型如图1

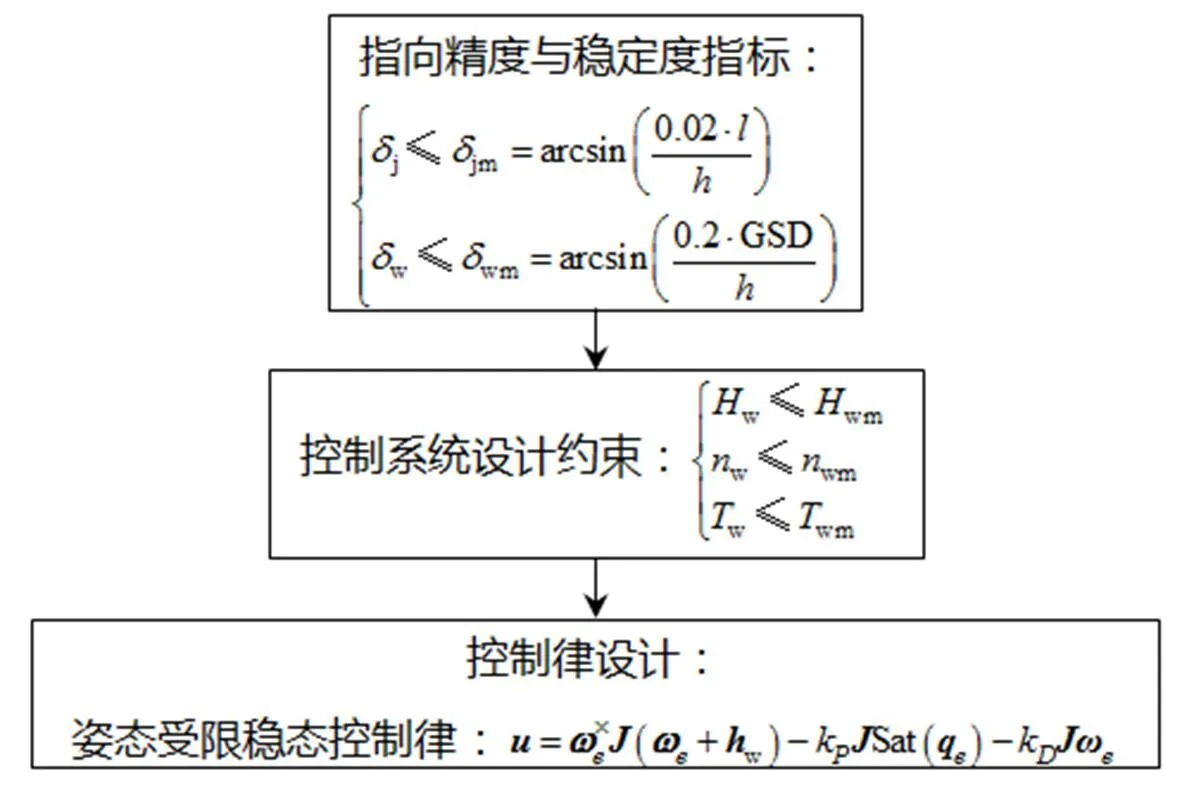
图1 控制分系统分析模型

2 协同优化框架

2.1 协同优化

协同优化的思想是将一个优化问题分为系统层与学科层。学科层与学科层之间保持着相对独立性，学科层之间不进行数据交互，而是通过与系统级之间的一致性约束信息进行信息交互，从而实现学科之间的参数解耦。系统层优化后将系统层的优化值向下传递给学科层，而各个学科层也将其优化后的优化值向上反馈给系统层。系统层优化的目标函数为原始的系统目标函数，约束函数是由各个学科优化问题最优解构成的集合，它用来解决学科之间以及学科与系统之间耦合变量的不一致性。在学科层，优化变量为本学科的状态变量、以及本学科优化所需的系统变量*、*；约束条件由不等式约束与等式约束组成，它们是状态变量、与设计变量的函数；最小化目标函数J则由它们之间状态变量的平方差形式构成。

协同优化的特点在于引入了一致性约束，在优化迭代过程中收敛趋近于0，由于的构造是系统层和学科层耦合变量的平方差形式，当逐步趋近于0时，各个学科之间以及学科与系统之间的耦合变量也就趋于统一，这就是协同优化解决参数耦合的关键，通过一致性约束协调了各个学科层的耦合关系。假设系统可以分为N个子学科，则协同优化的数学形式如图2所示。

2.2 罚函数处理约束

对于系统级一致性约束J的处理，可通过罚函数法将其加权到系统的目标函数中，通过惩罚项的作用迫使优化结果向满足一致性约束的方向靠近。即系统级优化目标转化为[15-16]：

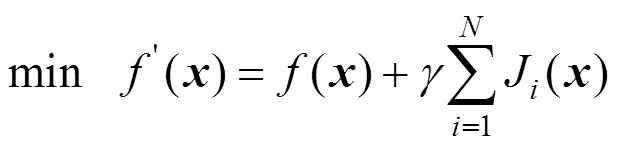
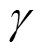
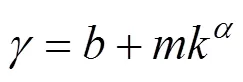
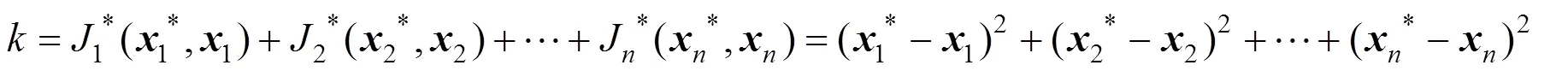
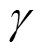
3 优化算法

基于上述建立好的优化模型，考虑优化问题的规模与变量类型以及约束的复杂度，选取相对应的合适的优化算法进行求解。对于总体优化，考虑到目标函数可能存在多峰性、非线性特点，可以考虑采用多岛遗传算法（Multi-Island Genetic Algorithm，MIGA），作为遗传算法的改进形式，它具有比传统遗传算法更为优良的全局求解能力和计算效率[17-19]。

对于分系统优化，针对变量类型为连续的分系统，本文采用序列二次规划算法（Sequential Quadratic Programming，SQP）进行求解，针对具有离散整型变量的分系统，采用混合整型优化算法（Multifunctional Optimization System Tool，MOST）。

表2 系统级和学科级优化算法选取

Tab.2 The selection of optimization algorithm

4 算例分析

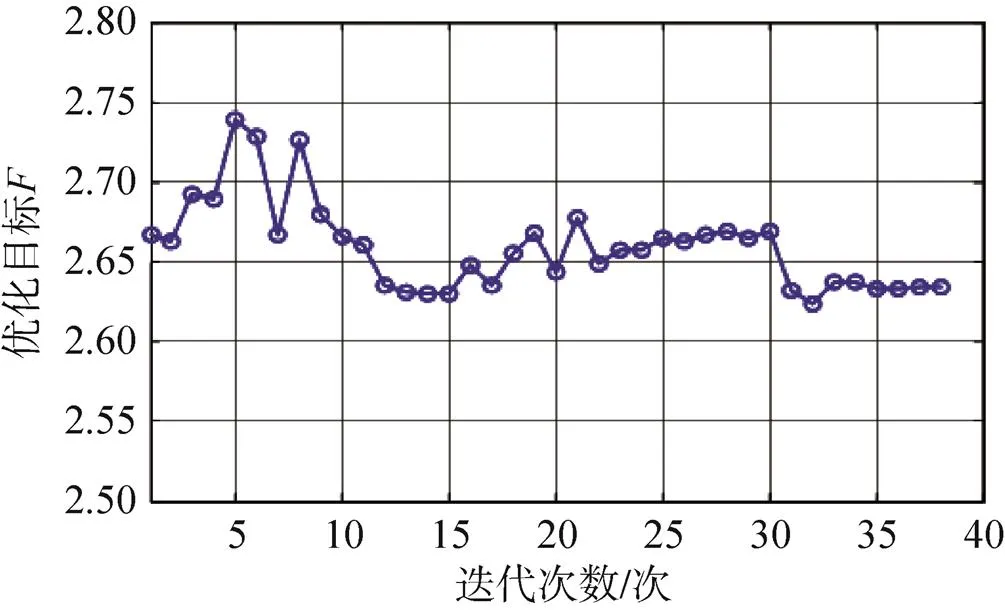
图3 优化目标迭代曲线

表3 总体优化结果

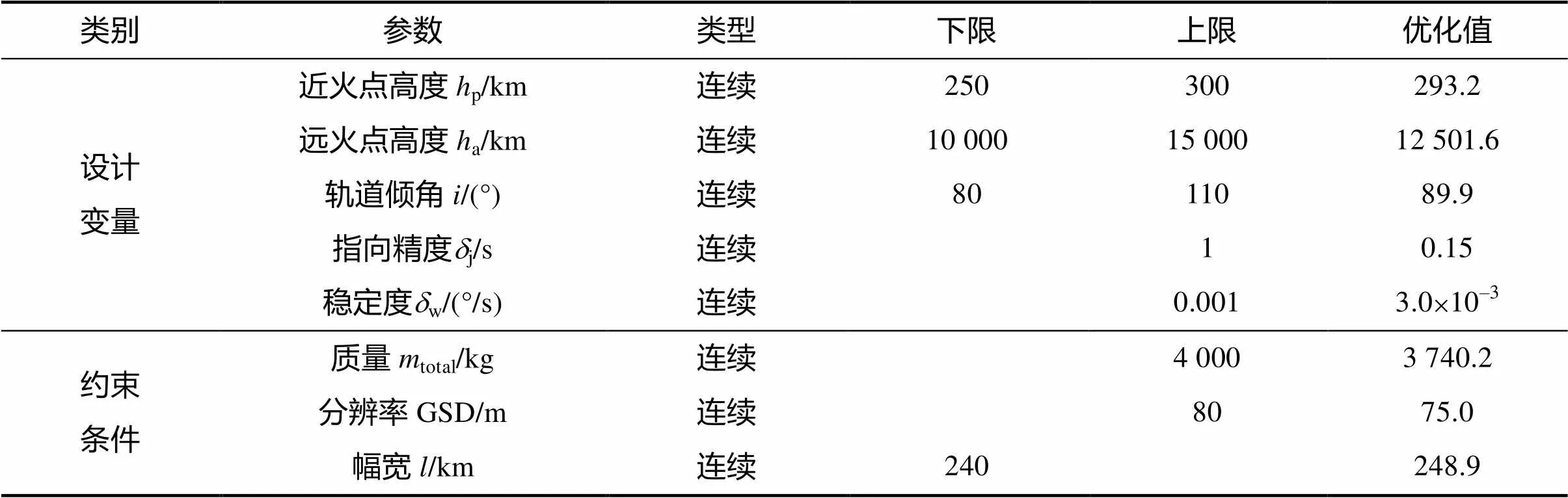
Tab.3 The result of system optimization

基于总体优化给出的指标结果，包括轨道参数以及分系统指标要求，将其作为分系统的设计输入，可以得到载荷学科与电源学科优化的结果如表4和表5所示。可以看出，不仅各分系统的设计变量的优化值满足上下限约束，约束条件也符合相应的要求。

表4 载荷学科优化结果

Tab.4 The result of the payload optimization

表5 电源学科优化结果

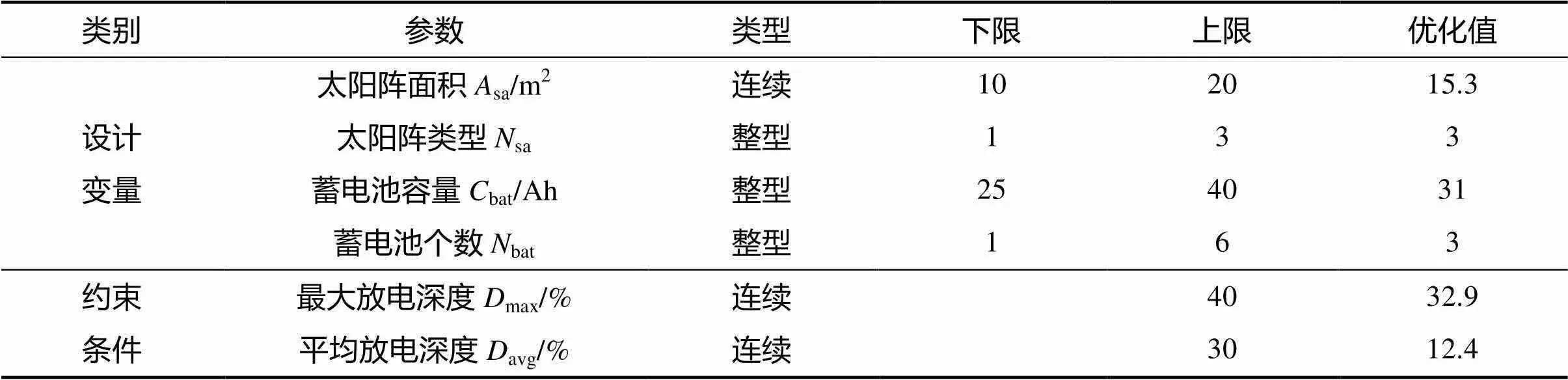
Tab.5 The result of the power optimization

探测器对火定向时，环绕器跟踪对火的仿真结果如图4~图7所示，从仿真结果可以看出，环绕器姿态角最终稳定于±0.05°，角速率最终稳定于±0.001 2°/s，满足总体优化表3中稳定度±0.003°/s与指向精度±0.15°的要求。

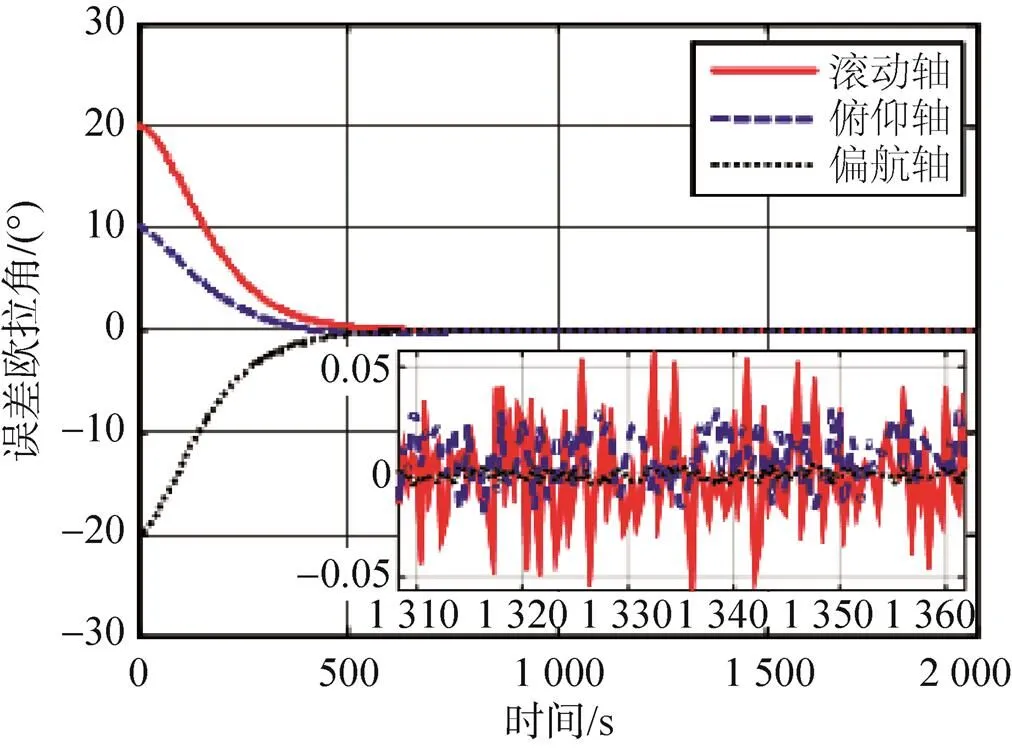
图4 三轴误差姿态角的响应

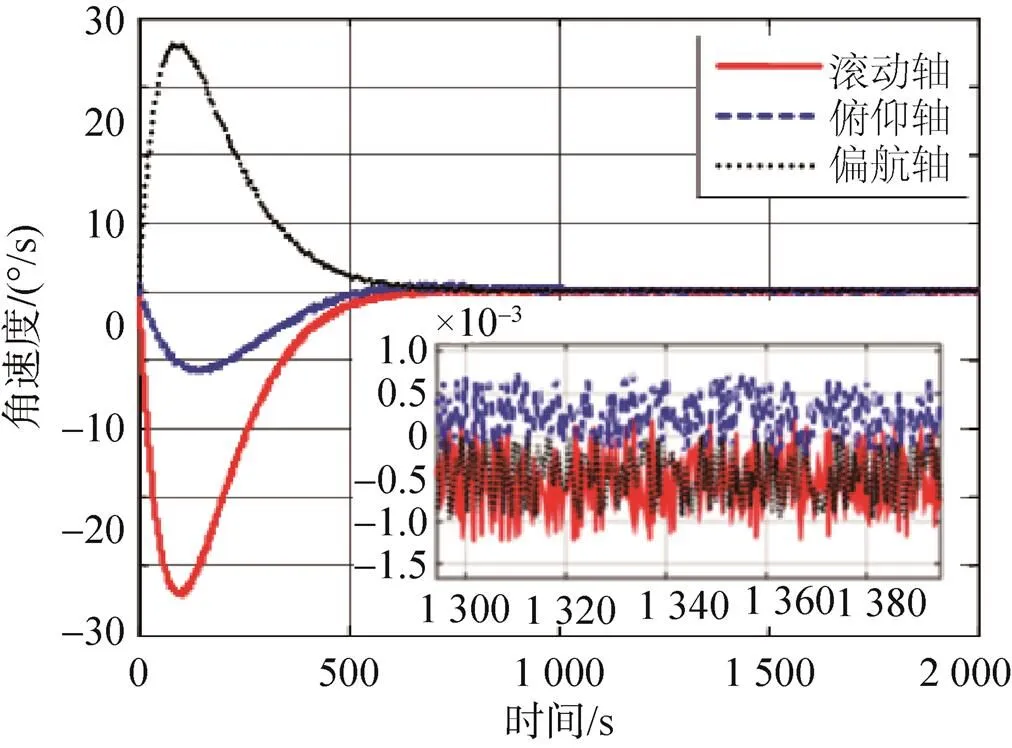
图5 三轴角速度的响应

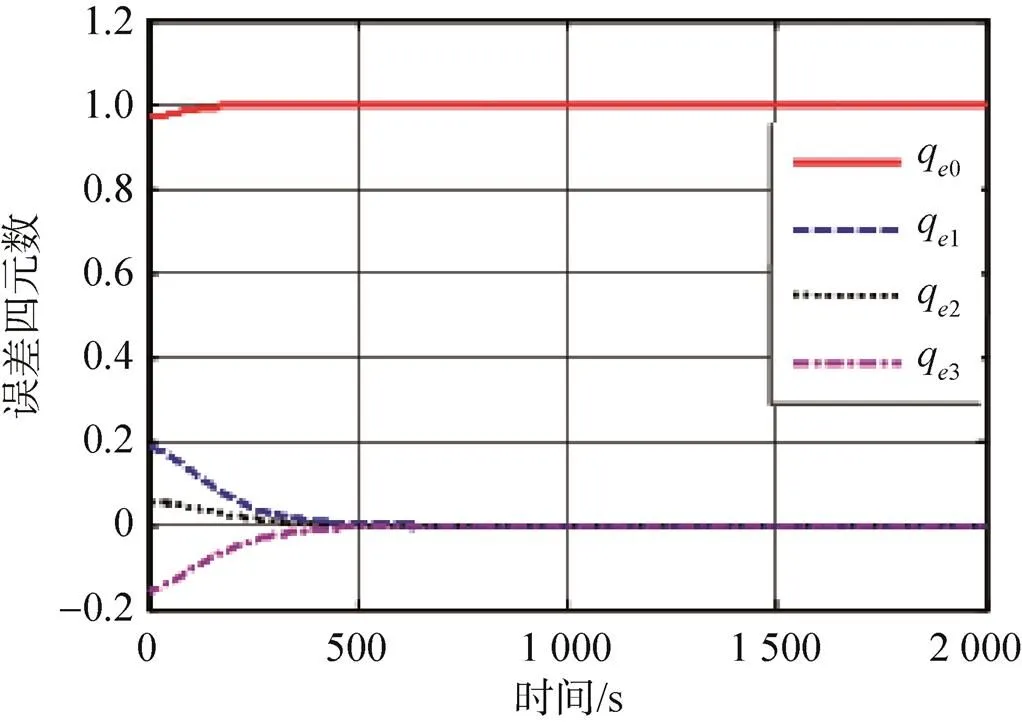
图6 误差四元数的响应

Fig.6 The response of quaternion error

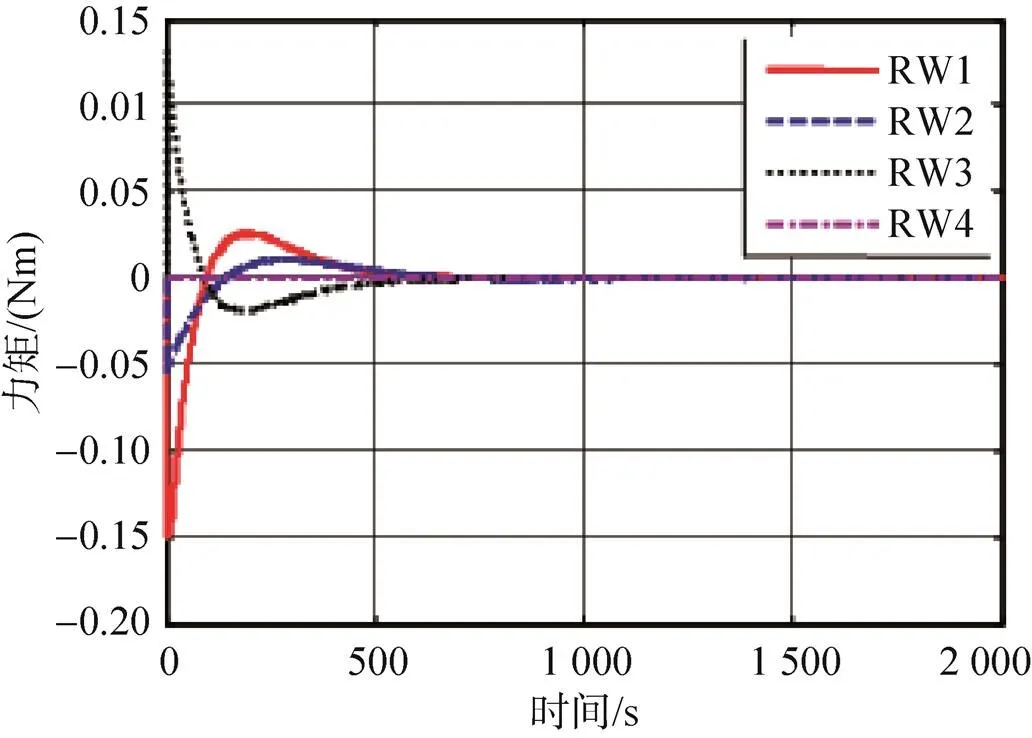
图7 飞轮控制力矩的响应

Fig.7 The response of control torque

5 结束语

本文以MDO方法作为火星探测器总体设计的理论指导，以探测器环火任务段为背景，建立对火全球遥感的总体优化模型与分系统优化模型，基于协同优化对总体优化与分系统优化之间的耦合关系进行协调，采用罚函数处理约束信息，选择MIGA算法作为总体优化算法，求解得到分系统设计指标要求；分系统则采用SQP算法和MOST算法进行优化，控制分系统采用姿态受限下的稳态控制律。整个优化与仿真结果满足指标和约束要求，从而验证了MDO方法应用于火星全球遥感探测器的合理性与有效性。

[1] 王振国, 陈小前, 罗文彩, 等. 飞行器多学科设计优化理论与应用研究[M]. 北京: 国防工业出版社, 2006.WANG Zhenguo, CHEN Xiaoqian, LUO Wencai, et al. Multi-disciplinary Design Optimization Theory and Application of Aircraft[M]. Beijing: Defense Industry Press, 2006. (in Chinese)

[2] BRAUN RD. Collaborative Optimization: An Architecture for Large-scale Distributed Design. Doctoral Dissertation[M]. Stranford University, California, 1996.

[3] YOU Zheng, LI Guanhua, FU Junming. A Distributed MDO Architecture and its Application on Small Satellite[C]. International Conference on Space Information Technology, 2009.

[4] HWANGJ, LEE D Y,CUTLER J,et al. Large-scale MDO of a Small Satellite Using a Novel Framework for the Solution of Coupled Systems and Derivatives[C]//Structural Dynamics and Materials Conference. Boston: AIAA, 2013.

[5] SANSCOUCIEMP, HULL P V, TINKER M L, et al. Lunar Habitat Optimization Using Genetic Algorithms[R].NASA/TP-2007-214852, NASA, 2007.

[6] WU Beibei, HUANG Hai, WU Wenrui. A Nonnested Collaborative Optimization Method for Multidisciplinary Design Problems[C]//2012 IEEE 16th International Conference on Computer Supported Cooperative Work in Design (CSCWD). Wuhan: IEEE, 2012: 148-52.

[7] HUANG Hai, AN Haichao, WU Wenrui, et al. Multidisciplinary Design Modeling and Optimization for Satellite with Maneuver Capability[J]. Structural & Multidisciplinary Optimization, 2014, 50(5): 883-898.

[8] 李大耀. 论航天火星探测[J]. 航天返回与遥感, 2003, 24(3): 59-62. LI Daoyao. On Mars Exploration by Space Probe[J]. Spacecraft Recovery & Remote Sensing, 2003, 24(3): 59-62. (in Chinese)

[9] 徐晴, 牛俊坡, 施伟璜, 等. 基于轨道器的火星着陆器定位及精度分析[J]. 航天返回与遥感, 2016, 37(6): 28-38.XU Qing, NIU Junpo, SHI Weihuang, et al. Positioning and Precision Analysis for Mars Lander Based on Orbiter Measurement[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(6): 28-38. (in Chinese)

[10] 彭玉明, 李爽, 满益云, 等. 火星进入、下降与着陆技术的新进展——以“火星科学实验室”为例[J]. 航天返回与遥感, 2010, 31(4): 7-14. PENG Yuming, LI Shuang, MAN Yiyun, et al. New Progress of Mars Entry, Descent and Landing Technologies——Mars Science Laboratory Case Study[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(4): 7-14. (in Chinese)

[11] 张凌燕. 基于iSIGHT卫星总体参数多学科优化研究[D]. 北京: 北京航空航天大学，2007. ZHANG Lingyan. Multidisciplinary Design Modeling and Optimization for Satellite Based on iSIGHT[D]. Beijing: Beijing University of Aeronautics and Astronautics, 2007. (in Chinese)

[12] 陈世平. 空间相机设计与试验[M]. 北京: 中国宇航出版社, 2003. CHEN Shiping. Space Camera Design and Experiment[M]. Beijing: China Aerospace Publishing House, 2003. (in Chinese)

[13] WERTZ J R, LARSON W J. Space Mission Analysis and Design[M]. Torrance, CA: Microcosm Press, 1992.

[14] 马世俊. 卫星电源技术[M]. 北京: 中国宇航出版社, 2001. MA Shijun. Satellite Power Technology[M]. Beijing: China Aerospace Publishing House, 2001. (in Chinese)

[15] 李海燕, 井元伟, 马明旭, 等. 基于动态罚函数法的协同优化算法[J]. 控制与决策, 2009, 24(6): 911-915. LI Haiyan, JING Yuanwei, MA Mingxu, et al. Collaborative Optimization Algorithm Based on Dynamic Penalty Function Method[J]. Control and Decision, 2009, 24(6): 911-915. (in Chinese)

[16] 李海燕, 马明旭, 黄章俊, 等. 自适应罚函数协同优化算法[J]. 系统仿真学报, 2009, 21(19): 6178-6182. LI Haiyan, MA Mingxu, HUANG Zhangjun, et al. New Adaptive Penalty Scheme for Collaborative Optimization[J]. Journal of System Simulation, 2009, 21(19): 6178-6182. (in Chinese)

[17] 明亮. 遗传算法的模式理论及收敛理论[D]. 西安: 西安电子科技大学, 2006. MING Liang. Genetic Algorithm Model Theory and Convergence Theory[D]. Xi'an: Xi'an University, 2006. (in Chinese)

[18] 李小将, 李新念. 一种基于多岛遗传算法的火力优化分配方法[J]. 装备指挥技术学院学报, 2011, 22(3): 119-123. LI Xiaojiang, LI Xinnian. A Method of Firepower Optimization Allocation Based on Multiple Island Genetic Algorithm[J]. Journal of the Academy of Equipment Command & Technology, 2011, 22(3): 119-123. (in Chinese)

[19] 赖宇阳. Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012. LAI Yuyang. Isight Parameter Optimization Theory and Examples of Detailed[M]. Beijing: Beihang University Press, 2012. (in Chinese)

（编辑：庞冰）

Multidisciplinary Modeling and Collaborative Optimization of Mars Global Remote Sensing Probe

LIU Mingxing ZHANG Heng ZHANG Wei

(Shanghai Institute of Satellite Engineering, Shanghai 201109, China)

According to the analysis of the system parameters of Mars global remote sensing probe, the system optimization model considering remote sensing performance and total weight was established to achieve the distribution of the overall requirements based on the idea of decomposition and optimization of MDO (Multidisciplinary Design Optimization), which can be regarded as the input conditions of the sub-system. Based on the requirements and some parameters delivered from system optimization, many disciplines of the Mars probe such as the payload, the power supply and the control were analyzed including the variables and the constraints, thus the subsystem optimization models were obtained. The cooperative optimization method was used to decouple the parameters in both system and subsystem optimization models. Based on the adaptive dynamic penalty function method and the multiple optimization algorithms, which help to improve the convergence rate, the optimal parameters of the probe were obtained by solving the system and the subsystems optimization models. Therefore, the validity of applying the MDO method to the general design of the detector was verified.

modeling; penalty function; collaborative optimization; multidisciplinary design Optimization; Mars probe

V423.4

A

1009-8518(2017)05-0057-11

10.3969/j.issn.1009-8518.2017.05.008

柳明星，男，1990年生，2017年获上海航天技术研究院控制科学与工程专业工学硕士学位，助理工程师。研究方向为卫星多学科设计与优化。E-mail: liumingxing_1990@163.com。

2017-05-02