多模型随机近似扰动算法的应用
2017-11-24张宇长江大学石油工程学院湖北武汉430100
张宇(长江大学石油工程学院,湖北 武汉 430100)
多模型随机近似扰动算法的应用
张宇(长江大学石油工程学院,湖北 武汉 430100)
油藏自动历史拟合属于复杂的大规模参数反演问题,地质参数的不确定性难以精确表征。基于随机扰动近似梯度算法(SPSA),提出了一种多模型随机近似扰动算法(EnSA)。该算法考虑多模型参数反演,降低了地质参数的多解性和不确定性;目标函数求解中应用SPSA算法避免了真实梯度计算。模型拟合结果表明:相比SPSA算法,EnSA算法降低了地质模型参数的不确定性,能够更精确地刻画油藏地层非均质性。
自动历史拟合;SPSA算法;EnSA算法?
油藏自动历史拟合中准确计算目标函数的梯度极其困难,梯度类算法稳定性差,求解过程异常复杂,如伴随法、有限差分法等。集合类算法如集合卡尔曼滤波算法容易产生滤波发散及梯度伪相关问题。随机扰动近似梯度算法(SPSA)作为一种有效的梯度近似算法,由于计算简单,其扰动搜索方向恒为上山方向且其期望值为真实梯度,是目前拟合问题常用的随机类算法,但SPSA算法只考虑单一地质模型,当初始地质模型与真实油藏差别较大时,该算法拟合所得油藏模型缺乏可靠性。为此,基于随机极大似然方法生成多个反映油藏特征的模型实现,在多模型拟合目标函数求解中应用SPSA算法,降低了地质模型的不确定性,提高了拟合后模型的可靠性。
1 随机扰动近似梯度算法(SPSA)
在第l迭代步,随机扰动梯度的计算公式为:
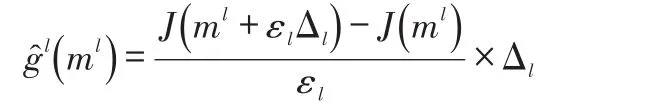
在第l+1迭代步所获得的控制变量为:
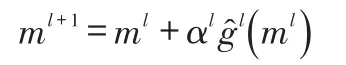
2 集合随机近似扰动算法(EnSA)
对于实际油藏历史拟合问题而言,操作矩阵C-M1(m-mpr)所需的计算代价在实际应用中难以承受,赵辉等[1,2]基于多模型对矩阵δM进行奇异值分解(SVD),将地质参数m降低到p域进行处理,大大降低了拟合参数的维数,有效地解决了大规模参数拟合问题。实际油藏地质模型不确定性强,为了更精确地刻画油藏地质属性,自动历史拟合算法需要考虑多模型进行拟合。它首先基于初始先验信息(ppr)和观测值(dobs)生成多个随机油藏模型实现(puc)及观测向量实现(duc):
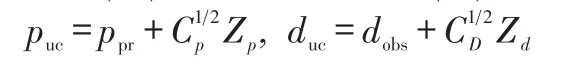
然后,对于每一对puc和duc,通过最小化目标函数JR(p)可获得相对应的MAP估计pc,并考虑随机变量pc的期望为:

pc的期望即为J(p)的MAP估计p∞。可以分别对每个模型实现puci采用SPSA算法进行反演得到MAP估计pci,然后求取pci的期望,即可获得油藏的MAP估计。
第j个模型实现pucj使用SPSA算法在第l迭代步,随机扰动梯度的计算公式为:
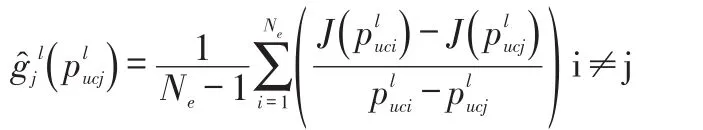
3 实例应用
基于所提出的集合随机近似扰动算法,首先对某概念油藏模型进行参数反演,并与SPSA算法结果进行对比分析。所建油藏模型真实渗透率场分布如图1(a)所示,初始模型渗透率场如图1(b)所示。分别基于SPSA算法和EnSA算法对概念油藏模型进行了参数反演,SPSA算法和EnSA算法的反演结果分别如图1(c)和图1(d)所示,由图1可知,初始渗透率模型与真实渗透率模型分布差异大,未能反映真实的高渗条带,经过SPSA算法和EnSA算法反演后渗透率分布均得到了较好改善,相比SP⁃SA算法,EnSA算法渗透率场拟合后更精确地刻画了高渗条带的位置。

图1 概念模型渗透率场(对数刻度)
4 结语
(1)基于降维的集合随机近似扰动算法(EnSA)能够在考虑初始油藏地质信息的基础上,对地质参数进行反演,在一定程度上降低了油藏自动历史拟合的多解性,降低了拟合参数的自由度。
(2)相比SPSA算法只考虑了单一模型,EnSA算法同时对多模型实现进行拟合,能够更好地考虑油藏地质信息的不确定性,更精确地刻画油藏地层非均质性。
[1]赵辉,曹琳,李阳等.基于改进随机扰动近似算法的油藏生产优化.石油学报,2011,06):1031—1036.
[2]Zhao H,Li G,Reynolds A C,et al.Large-scale histo⁃ry matching with quadratic interpolation models[J].Computa⁃tional Geosciences,2013,17(1):117-138.
[3]Sarma P,Chen W H,Durlofsky L J,et al.Production Optimization With Adjoint Models Under Nonlinear Control-State Path Inequality Constraints
