基于Smith-PID的数字PCR检测仪液路双闭环比值控制系统的设计

陈庆明,刘经龙,李冬梅

广东顺德工业设计研究院(广东顺德创新设计研究院)a.精密仪器部;b.电子信息部,广东 佛山 528311

基于Smith-PID的数字PCR检测仪液路双闭环比值控制系统的设计

陈庆明a,刘经龙b,李冬梅a

广东顺德工业设计研究院(广东顺德创新设计研究院)a.精密仪器部;b.电子信息部,广东 佛山 528311

液路系统输出液体的精度、速度、稳定性是数字PCR检测仪实现功能的基础.针对基于微流控芯片的数字PCR检测仪中液路系统出现的大阻力、大滞后的问题,本文提出基于Smith-PID算法的双闭环控制系统的液路结构.根据注射泵、控制对象的数学模型以及Smith预估控制器原理,构建双闭环比值控制系统,并利用Simulink对于系统进行建模和仿真,得到相比于传统PID较好的系统的响应曲线.在数字PCR检测仪的液路系统验证中,对比响应曲线发现,与传统PID控制的双闭环液路相比,Smith-PID控制的双闭环比值控制系统的样品调节时间减少2/3,稀释液调节时间减少1/3,稳态误差减少8%,提高了系统流量输出的稳定性、准确性、快速性.

数字PCR;Smith-PID控制;双闭环比值控制;液路系统

引言

液滴式数字PCR主要分成液滴生成、PCR扩增、荧光检测3个部分,数字PCR检测仪是的荧光信号检测分析部分.液路系统作为数字PCR检测仪的重要部分,将含有荧光染色的DNA片段的液滴,与作为稀释液的油,按照一定关系注入检测的微流控芯片,利用微流控芯片的结构以及液滴和稀释油关系,使得液滴按依次单个通过微流控芯片的检测段[1-2].控制液滴和稀释油的流速是保证液滴完整、保证液滴单个通过微流控芯片的前提,也是后续信号检测的保证,是整个基于微流控芯片的数字PCR检测仪的核心技术之一[3-4].

传统的液流系统主要采用传统的PID控制器或者模糊PID控制方法,此方法在较大的通道、阻力较小、滞后效应不严重的液流系统是有效的[5-6].但是,在医疗设备的小体积、少样品、精密化的过程中,微流控芯片技术作为创新有效的技术引入到医疗器械中.微流控芯片的结构和流道相比于传统的流道小得多,管道尺寸在毫米量级,因此,微流控芯片的阻力比起传统的管路阻力要大得多,传统液路出现的问题以及解决的方法,并不完全适用于基于微流控芯片检测的液路系统[7-8].

数字PCR检测仪是基于微流控芯片研制的医疗检测设备,其中的液流系统是大阻力、大滞后的非线性系统,并且作为动力源的注射泵输出存在脉动,对液流系统控制流量存在干扰,反馈调节参数滞后,特别在阻力很大的微流控液路系统中,实时精确控制液滴和稀释液的流速存在困难[9-12].

为解决以上问题,本文研究将Smith-PID控制器与液路系统的结构相结合,建立Smith-PID双闭环比值控制系统,建立基于Smith-PID的双闭环比值控制系统仿真模型,结果显示该控制对于液滴样本和稀释液两者的流速控制有很好的准确性,增强液滴样本和稀释油之间的联系,减轻原系统的严重滞后现象.

1 数字PCR检测仪液路双闭环控制系统结构

数字PCR检测仪液路系统的流量流速的设定由控制界面输入,经过控制器的处理,控制信号经过驱动器驱动注射泵的步进电机,通过控制信号的变化达到流体流量速度的目的.又经过流量传感器,将反馈值与设定值比较,实时调节,实现输出的流量速度控制在目标稳定值.简化液路系统模型,进行建模,单液路控制原理,见图1.

图1 液路系统单回路控制原理图

为克服液流的滞后问题,实现液路系统输出的流量速度的精确控制和解决样本液滴与稀释油之间的相关性问题,使用流量传感器的流量反馈,在系统中建立起样本和稀释液的各自的闭环控制以及样本与稀释液之间的比值控制,其中,控制算法采用Smith-PID算法,双闭环比值控制的结构,见图2.

2 数字PCR检测仪控制系统的数学模型

注射泵和驱动器的传递函数[13-14]:

查询所用电机参数[15],经过换算得到电机的传递函数为:

流量传感器是比例环节[16],设为k1;

液体的流量速度关系[17-18],根据泊肃叶公式:

D是管路直径;p是压力;L是管路长度;μ是液体的粘度;Q是流量速度.

可以简化成:

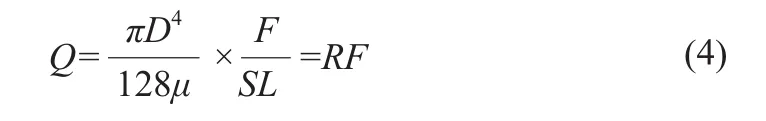
拉普拉斯转换[19],化得理想状态下控制对象的传递函数:

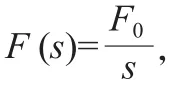
因此,

根据上述结构的数学模型和传递函数,对应图2的数字PCR检测仪的双闭环比值控制系统,整理并化简框图,得到框图,见图3.

图2 数字PCR检测仪液路系统双闭环比值控制系统结构

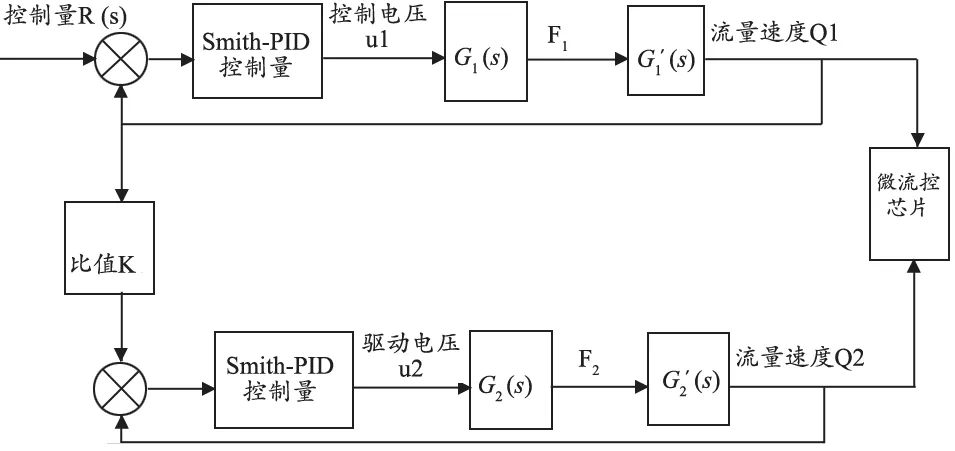
图3 液路系统双闭环比值控制系统数学模型

其中:

3 数字PCR检测仪液路系统的Smith-PID控制算法的研究

3.1 Smith-PID控制原理

在两个闭环回路中主要采用是Smith-PID控制,Smith-PID预估控制是在原来PID控制器的基础上,针对大时延过程的预估补偿,其原理是按照客观过程的特性预估出一种模型加入到反馈PID控制系统中,使被延时了τ时间的被控量超前反映到调节器的输入端,使调节器提前动作,从而明显地减小超调量和加速调节过程.Smith-PID控制系统模型,见图4.

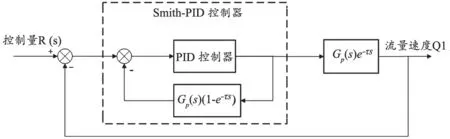
图4 Smith-PID控制系统模型

对照图3建立的控制系统及其数学模型,单闭环控制系统中:

PID控制器的传递函数为:

此时单回路的闭环传递函数为:

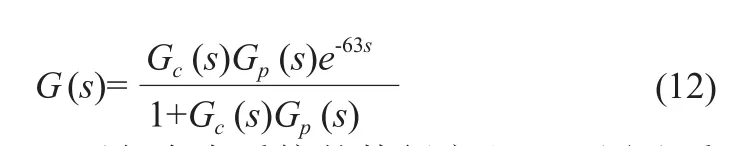
可以看出,已不包含在系统的特征方程里,因此系统性能完全不受纯时延环节的影响.从原理上,设计的Smith-PID闭环控制系统完全不存在滞后效应..

3.2 数字PCR检测仪液路系统的Smith-PID控制算法研究及仿真

Smith-PID控制算法是在PID控制算法基础上,针对数字PCR检测仪的滞后问题,把Smith预估控制增加进控制系统里面,目的是减少系统控制的滞后.本文主要在Simulink上仿真来研究算法的优劣,首先在仿真调节基于PID算法的单闭环控制系统[20],见图5 ,依次调节好比例、积分和微分控制器的参数,不断修改和仿真,最终得到的响应输出,见图6.

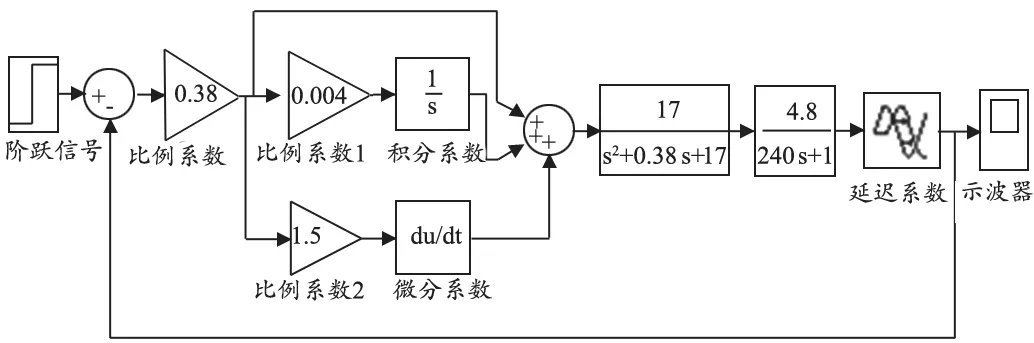
图5 基于PID算法的单闭环控制系统

图6 基于PID算法的单闭环控制系统输出响应

从以上仿真结果可以看出,系统的静差为ess=0,超调量σ=1.9%,调节时间ts=285 s,这是整体效果较好的PID参数.在这基础上如果增加比例环节或者微分环节,加快调节速度,会增加系统从超调量,对于仪器设备来说会有损耗,甚至会对系统的稳定性造成影响.

在图5设置的较好的PID参数基础上,增加Smith预估控制环节,见图7,进一步优化调节PID参数,得到较好的结果,见图8.

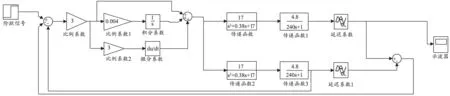
图7 基于Smith-PID算法的单闭环控制系统

图8 基于Smith-PID算法的单闭环控制系统输出响应

系统的静差为ess=0,超调量σ=0,调节时间ts=134 s.对比图6和图8两种算法输出响应可以看出,在基于微流控芯片的数字PCR检测仪的液路系统中,Smith-PID控制算法比传统的纯PID控制算法具有更快的调节速度,缩短调节时间,有效减轻液路系统的滞后现象,控制效果更好.

4 基于Smith-PID的液路控制系统的验证和结果分析

4.1 基于Smith-PID的数字PCR检测仪液路双闭环比值控制系统仿真验证

在数字PCR检测仪的液路双闭环比值控制结构上,Simulink中建立传统PID控制算法的双闭环比值控制仿真模型,见图9,其中结合实际需要,比值为2.仿真效果,见图10.

图9 基于PID算法的双闭环比值控制系统

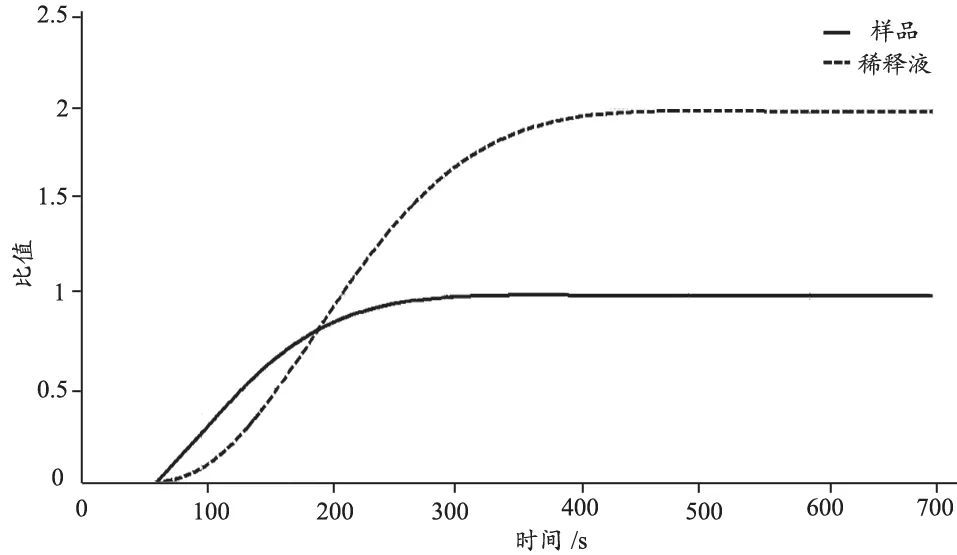
图10 基于PID算法的双闭环比值控制系统输出响应

图10为传统PID双闭环比值控制系统的输出响应Simulink仿真图,主回路-样品控制回路的调节时间为,ts=285 s由于副回路目标值较高是主回路的两倍,所以会增加调节时间,最终稀释液调节时间为ts=404 s.

在对数字PCR检测仪的液路双闭环比值控制系统结构研究,以及数学模型和单闭环Smith-PID最优参数的基础上,本文提出基于Smith-PID的数字PCR检测仪液路双闭环比值控制系统,建立基于Smith-PID控制算法的双闭环比值控制仿真系统,见图11,其中结合实际需要,比值为2.仿真的输出效果,见图12.

如图12为基于Smith-PID算法的双闭环比值控制系统的输出响应Simulink仿真图,其中主回路-样品控制回路保持了Smith-PID算法的单闭环控制算法的控制效果,样品的调节时间为ts=134 s,由于副回路目标值较高是主回路的两倍,所以会增加调节时间,最终稀释液调节时间为ts=168 s.

从Simulink的仿真图图10和图12对比可以得出,控制系统从传统PID算法改进到Smith-PID控制算法时候,样品调节时间从285 s减少到134 s,减少了151 s;稀释液的调节时间从404 s减少到168 s,减少了236 s,很大提高控制性能.

4.2 数字PCR检测仪液路控制系统的验证

根据液路系统双闭环比值控制原理,系统主要由注射泵、电磁阀、微流控芯片、流量传感器、管路、接头等组成.系统工作如下:样本注射泵和稀释液注射泵对液体推进,样品液和稀释液进入微流控检测芯片,根据样品的流量,计算机控制注射泵的速度,按比值调节稀释液的流量;调节过程中,一方面样品流量根据设定值,运用Smith-PID控制算法,不断调节达到目标值,另一方面,稀释液根据样品流量,运用Smith-PID控制算法,不断调节达到样品流量的某个比值.

在数字PCR检测仪的测试液路系统中,采用传统PID的双闭环比值控制,如同图9的仿真模型,采集的流量输出响应得到响应曲线,见图13.

图13上可以得出传统PID控制系统性能参数,控制系统中样品调节时间为ts=302 s,稀释液调节时间为ts=358 s,与仿真的输出响应基本吻合;此外,可能因为积分饱和的原因,存在约为10%输出静差.

图11 基于Smith-PID算法的双闭环比值控制系统

图12 基于Smith-PID算法的双闭环比值控制系统输出响应

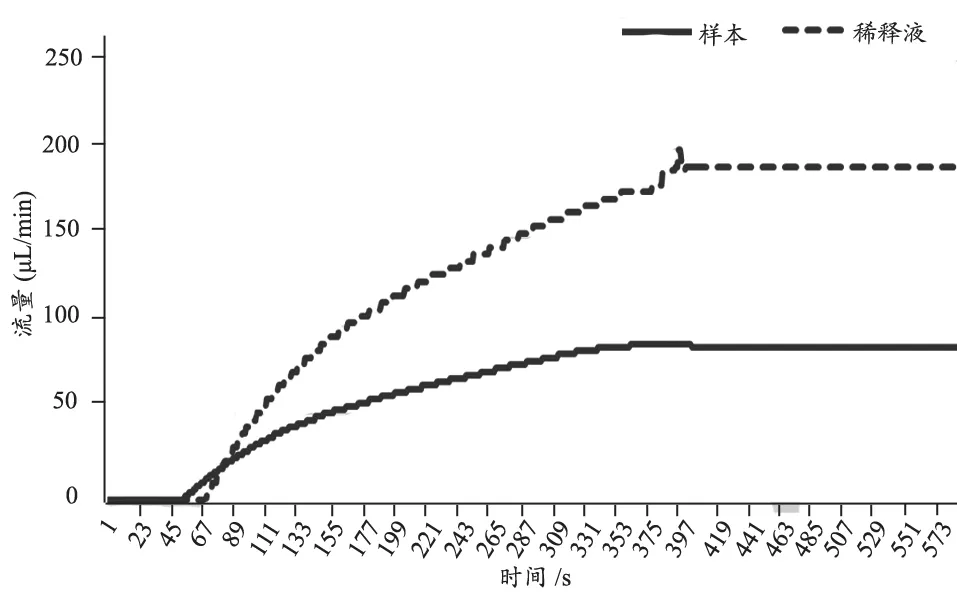
图13 传统PID控制下液路流量的输出响应

在数字PCR检测仪的测试液路系统中,采用Smith-PID的双闭环比值控制,如同图11仿真模型,采集的流量输出响应得到响应曲线,见图14.

如图14的数字PCR检测仪的液路流量响应曲线,趋势上与仿真一致,但是在样本回路即主回路中,调节时间为ts=111 s,中间由于电机脉冲和传感器的影响,输出流量存在一定的脉动,但是脉动没有超过2%,对于仪器的检测效果没有影响;而稀释液回路即副回路中,实际上的超调时间ts=193 s,此误差更多是因为在样本进入芯片过程中对于稀释液回路的影响,本文在建模过程中简化了样本与稀释液之间的作用.

图14 Smith-PID控制下液路的输出响应

4.3 验证的结果分析及讨论

从式(3)泊肃叶公式可以看出,在基于微流控的数字PCR液路系统中,因为内径小在几十微米的数量级,而且油的粘度大,粘度大约为水粘度的300多倍,这样的对象系统下,流体的阻力较大大,流体滞后现象较为严重;从图13也可以看出,在样品给定阶跃为100,稀释液与样品比值为2的控制给定值下,在微流控芯片的液路控制中,采用的传统PID控制存在着响应速度仍然较慢,稳态误差较为严重.

同样的给定值和比值控制,对比图13和图14可以看出,与传统的PID控制器相比,加入了Smith-PID控制器的PCR检测仪的液路系统在性能上有很大的提高,样品的调节调节时间从由302 s减少为111 s,缩短了约2/3时间;稀释液的调节时间由359 s减少为193 s,缩短了约1/3时间;输出的静态误差从10%减小到2%,减少了8%.此外,缩短调节时间不仅提高仪器的整体性能,而且还有利于消减积分饱和,减小系统的稳定误差,使得系统更加稳定.

本文主要针对微流控芯片中流体控制的大阻力、大滞后的问题,提出与传统液路系统不同的新型微流控液路系统中的滞后问题的解决方法,采用Smith-PID控制比起常用的纯PID也有更好的效果.不足之处,本文研究的算法没法克服PID本身的缺点,以及Smith预估对于模型的要求,如果建立的模型不够准确或者简化某些环节,可能存在图14中的稳态偏差.因此,在使用改算法和控制系统,需要对于对象的数学模型的深入了解和长时间的实际试验及修正.

5 总结

针对基于微流控芯片的数字PCR检测仪中,相较于传统PID控制下的液路系统流量的控制,Smith-PID控制器能够更好的克服流体的大阻力、大滞后问题.引入Smith-PID控制器的液路双闭环比值控制系统,较好的克服微流控芯片中流体的大阻力、大滞后问题;同时相较于传统的PID控制下,输出样品的调节时间缩短了约2/3,稀释液的调节时间缩短了约1/3, 稳态误差减小8%,减少了调节时间,提高了调节的效率,有利于减小积分饱和对于系统的影响,提高系统输出流量的精度和稳定性.因此,在数字PCR检测仪的液路中,引入基于Smith-PID控制器的双闭环比值液路控制系统,在系统的稳定性、准确性、快速性都有很好的控制效果.

[1] 吴坚,曹文祺.聚合酶链式反应(PCR)荧光检测研究[J].计量学报,2002,23(2):151-156.

[2] 薛巍,姜雯,苏荣国.微流控芯片检测技术进展[J].化学分析计量,2007,16(3):77-79.

[3] 冯众颖,周兆英,叶雄英.微流体驱动与控制技术研究进展[J].液压与气动,力学进展,2002,32(1):1-15.

[4] Sugiura S,Edahiro J,Kikuchi K,et al.Pressure-driven perfusion culture microchamber array for a parallel drag cytotoxicity assay[J].Biotechnol Bioeng,2008,100(6):1156-1165.

[5] 王志超,董明利,刘超.基于模糊PID的流式细胞仪液流主从控制系统[J].液压与气动,2017,(2):45-50

[6] 赵国普.液压元件试验台计算机辅助检测系统的研究[J].机床与液压,1999,5:77-80.

[7] El-Ali J,Sorger PK,Jensen KR.Cells on chips[J].Nature,2006,442(7701):403-411.

[8] Muto T,Yamada H,Suematsu Y.Digital control of hydraulic actuator system operated by differential pulse width modulation[J].JSME Int,1990,33(4):641-648.

[9] Owens DH,Raya A.Robust stability of smith predictor controllers for time delay systems[J].IEE Proc. Part D,1982,129(6):298-304.

[10] 张峻颖,杨马英,谢启.含有纯滞后系统的控制方法[J].控制工程,2002,9(6):91-93.

[11] 程启明,王勇浩.基于Smith预估的模糊/PID串级主汽温控制系统仿真[J].电工技术学报,2007,22(3):143-147

[12] 陈莉,张锋.串级-Smith预估控制在温度大滞后系统中的应用[J].仪表技术,2007,(2):37-39.

[13] 程树康,刘宝延.步进电动机及其驱动控制系统[M].哈尔滨:哈尔滨工业大学出版社,2007.

[14] 姜德美,谢守勇,甘露萍.步进电机启动控制算法设计[J].西南大学学报(自然科学版),2007,(5):129-132

[15] 王邦继,刘庆想,周幕,等.步进电机速度曲线的设计与FPGA实现[J].微电机,2012,45(8):67-71.

[16] 耿德根.AVR高速嵌入式单片机原理与应用[M].北京:北京航空航天大学出版社,2002.

[17] 邵裕森.过程控制及仪表[M].上海:上海交通大学出版社,2008.

[18] 陈伟,张联志,徐蒙.灌浆压力稳定性控制的流体力学模型研究[J].应用力学学报,2013,30(1):65-69.

[19] 王建辉,顾树生.自动控制原理[M].北京:清华大学出版社,2005.

[20] 陈永清,黄金.基于Simulink的复合节流调速系统仿真分析[J].液压与气动,2011,(10):15-17.

本文编辑 袁隽玲

Design of Double Closed Loop Ratio Control System of the Digital PCR Detector Based on Smith-PID

CHEN Qingming, LIU Jinglong, LI Dongmei
a.Department of Precision Instrument; b.Department of Electronic Information, Guangdong Shunde Industrial Design Institute(Guangdong Shunde Innovative Design Institute), Foshan Guangdong 528311, China

The precision, speed and stability of the liquid output of the liquid system are the basis of the function of the digital PCR detector. In order to solve the problem of large resistance and large delay in the liquid circuit system of the digital PCR detector,the structure of the double closed loop control system based on the Smith-PID algorithm was proposed. A double closed loop ratio control system was constructed according to the injection pump, the control object model and Smith controller principle. In addition,modeling and simulation was performed on the system for the use of Simulink, and a better response curve was obtained compared to the traditional PID. In the digital PCR detector liquid circuit system verification, we found that compared with the traditional double closed loop liquid path of PID control, the settling time of the double closed loop ratio control system Smith-PID control samples reduced 2/3, dilution adjustment time reduced 1/3, the steady-state error reduced 8%. In conclusion, the Smith-PID control algorithm can improve the rapidity, accuracy and stability of the flow output system.

digital PCR; Smith-PID control; double closed loop ratio control; liquid system

TP27;TP774 < class="emphasis_bold">[文献标识码] A

A

10.3969/j.issn.1674-1633.2017.10.009

1674-1633(2017)10-0033-06

2017-05-08

2017-05-23

作者邮箱:653911982@qq.com