半函数部分线性模型的经验似然推断

胡玉萍， 薛留根， 冯三营

(1.北京工业大学 应用数理学院 北京 100024； 2.郑州大学 数学与统计学院 河南 郑州 450001)

DOI: 10.13705/j.issn.1671-6841.2016356

半函数部分线性模型的经验似然推断

胡玉萍1，2， 薛留根1， 冯三营2

(1.北京工业大学 应用数理学院 北京 100024； 2.郑州大学 数学与统计学院 河南 郑州 450001)

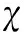
半函数部分线性模型； 经验似然; 函数型数据; 置信域

DOI: 10.13705/j.issn.1671-6841.2016356

0 引言

对函数型数据的分析和处理是统计学的一个热门问题,被广泛应用到计量经济学、生物医学、心理学及其他领域.考虑半函数部分线性模型

其中：Y是实值响应变量；X是取值于Rp上的随机向量；m(·)是未知的光滑实函数；T是取值于抽象无穷维空间H上的函数型协变量；|是随机误差,期望为零,方差有限,且与X和T是独立的.

文献[1]引入了函数线性模型,文献[2-3]利用函数主成分分析法研究了函数型线性回归模型的估计及预测问题.为了更好地拟合数据,一些学者开始研究函数型数据半参数模型.文献[4] 提出了半函数部分线性模型(SFPLM),利用函数核光滑方法并结合最小二乘法给出了参数分量和非参数分量的估计,得到了参数分量的渐近正态性和非参数分量的收敛速度.文献[5]进一步将SFPLM推广应用于时间序列预测问题.文献[6]基于惩罚函数对SFPLM的高维线性回归部分进行了变量选择,得到变量选择的oracle性质及非参数分量的非参收敛速度.文献[7]利用主成分基函数展开及最小二乘法研究了部分函数线性模型的均方预测误差的收敛速度.文献[8]考虑了纵向函数型数据变系数模型,给出了模型中系数函数和历史指标函数的估计,证明了它们的渐近性质.文献[9]研究了纵向函数型数据单指标模型,将经典单指标模型的最小平均方差估计(MAVE)方法推广到函数型数据情形.文献[10]研究了部分函数变系数模型,利用主成分基函数展开及局部光滑法得到了系数函数的估计.

1 估计方法

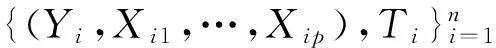
其中|i是相互独立的模型误差,且E(|i|Xi,Ti)=0,Var(|i|Xi,Ti)=σ2lt;∞,i=1,2,…,n.Ti∈H1,H1是H的紧子集.X=(X1,…,Xn)T,Xi=(Xi1,…,Xip)T,Y=(Y1,…,Yn)T.

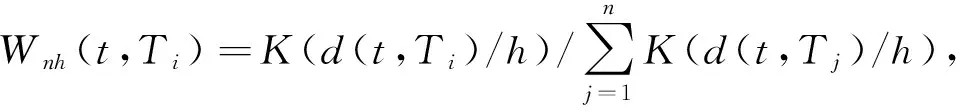
Yi-E(Yi|Ti)=[Xi-E(Xi|Ti)]Tβ+|i.

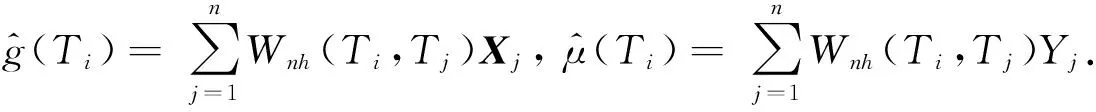
其中λ为Lagrange乘子,满足

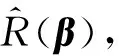
2 主要结果

为叙述方便,始终假设c表示一不依赖于n的正的常数,c每次出现可以取不同的值.引入记号:

B(t,h)={t′∈H:d(t,t′)≤h},qij=Xij-E(Xij|Ti),qi=(qi1,…,qip)T，

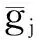
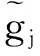
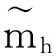
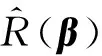
(C1)K满足Lipschitz条件，支撑为[0,1]，并且∃c满足∀u∈[0,1],-K′(u)gt;cgt;0.

(C2) 存在一个(0，∞)上的正值函数φ和正值c0、c1、c2使得

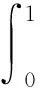
(C3) 存在常数cgt;0，αgt;0，∀f∈{m，g1,…,gp}, 都有|f(u)-f(v)|≤cdα(u,v).

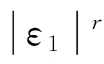
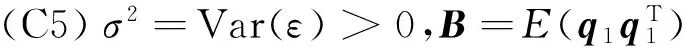
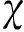
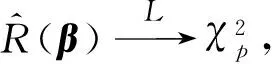
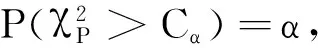
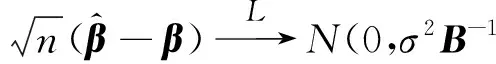
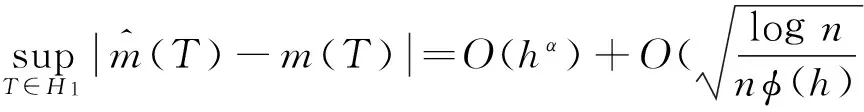
3 定理证明

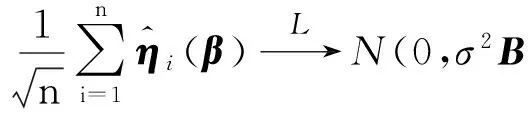
令Sn1j表示Sn1的第j个分量,则有

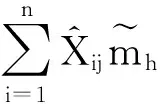
a.s.=

由式(5)～(7)可知Sn1j=Op(n1/2).

令Sn2j表示Sn2的第j个分量,类似可证Sn2j=Op(n1/2)，则，

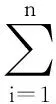
Anij表示Ani的第j个分量,则有

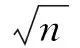
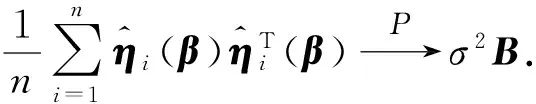
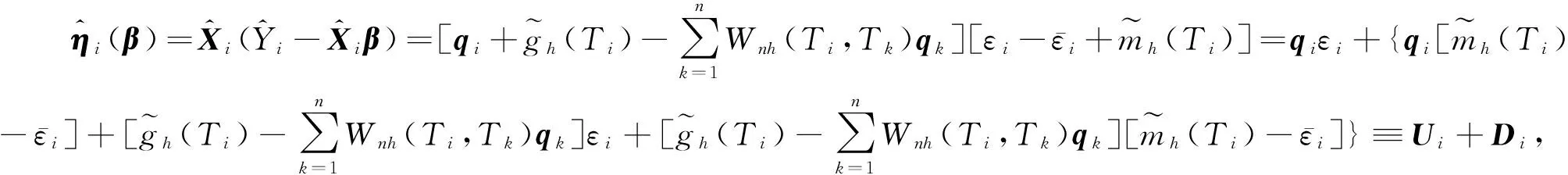
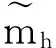
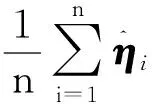
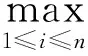
证明利用引理1的证明方法及文献[11]可证得上式.

定理1的证明由式(4)可得

由引理1～3可以证得

由引理1及2可证明定理1.

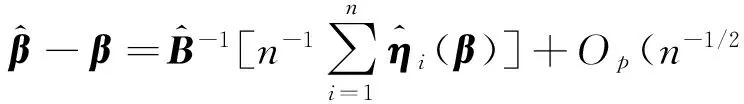
定理3的证明计算可得

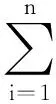
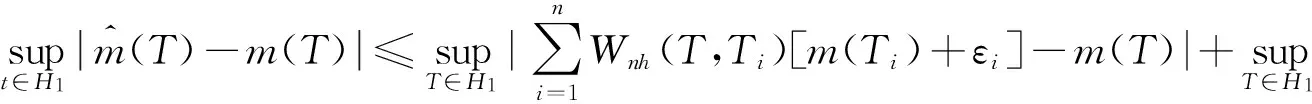
由文献[4]中定理2可得本定理证明.

[1] RAMSAY J O, SILVERMAN B W. Functional data analysis [M]. New York: Springer, 1997.

[2] CAI T T, HALL P. Prediction in functional linear regression [J]. Annals of statistics, 2007, 34(5): 2159-2179.

[3] HALL P, HOROWITZ J L. Methodology and convergence rates for functional linear regression [J]. Annals of statistics, 2007, 35(1): 70-91.

[4] ANEIROS-PEREZ G, VIEU P. Semi-Functional partial linear regression [J]. Statistics and probability letters, 2006, 76(11): 1102-1110.

[5] ANEIROS-PEREZ G, VIEU P. Nonparametric time series prediction: a semi-functional partial linear modeling [J]. Journal of multivariate analysis, 2008, 99(5): 834-857.

[6] ANEIROS-PEREZ G, VIEU P. Testing linearity in semi-parametric functional data analysis [J]. Computational statistics, 2013, 28(2): 413-434.

[7] SHIN H. Partial functional linear regression [J]. Journal of statistical planning and inference, 2009, 139(10): 3405-3418.

[9] JIANG C R, WANG J L. Functional single index models for longitudinal data [J]. Annals of statistics, 2011, 39:362-388.

[10] FENG S, XUE L G. Partially functional linear varying coefficient model [J]. Statistics, 2016, 50(4): 1-16.

[11] OWEN A B. Empirical likelihood ratio confidence intervals for a single function [J]. Biometrika, 1988, 75(2): 237-249.

[12] OWEN A B. Empirical likelihood ratio confidence regions [J]. Annals of statistics,1990, 18(1): 90-120.

[13] WANG Q H, JING B Y. Empirical likelihood for partial linear models with fixed design [J]. Statistics probability letters, 1999, 41(4): 425-433.

[14] CUI H J, CHEN S X. Empirical likelihood confidence region for parameter in the errors-in-variables models [J]. Journal of multivariate analysis, 2003, 84(1): 101-115.

[15] ZHU L X, XUE L G. Empirical likelihood confidence regions in a partially linear single-index model [J]. Journal of the royal statistical society, 2006, 68(3): 549-570.

[16] 胡玉萍，冯三营，薛留根. 部分函数线性模型的经验似然推断[J]. 应用概率统计, 2015, 31(2):146-158.

[17] FERRATY F, VIEU P. Nonparametric functional data analysis [M]. New York: Springer, 2006.

[18] 高集体, 洪圣岩, 梁华. 部分线性模型中估计的收敛速度[J]. 数学学报, 1995, 38(5): 658-669.

[19] 赵培信. 半参数变系数部分线性模型的统计推断[D]. 北京：北京工业大学, 2010.

[20] XUE L G, ZHU L X. Empirical likelihood semiparametric regression analysis for longitudinal data [J]. Biometrika, 2007, 94(4): 921-93.

(责任编辑：方惠敏)

EmpiricalLikelihoodInferenceforSemi-functionalPartialLinearModel

HU Yuping1,2， XUE Liugen1， FENG Sanying2

(1.CollegeofAppliedSciences,BeijingUniversityofTechnology,Beijing100024,China； 2.SchoolofMathematicsandStatistics,ZhengzhouUniversity,Zhengzhou450001,China)

The estimation for semi-functional partial linear model was considered. The empirical likelihood method was developed to make inference for parameter of interest. The empirical likelihood ratio for the parameter was constructed, and it was asymptotically standard chi-square distribution. Therefore, the corresponding confidence region of the parameter was constructed. At the same time, the estimator of the nonparametric function was given, and the theoretical property of the convergence rate was studied under certain regular conditions.

semi-functional partial linear model; empirical likelihood; functional data; confidence region

2016-12-29

国家自然科学基金项目(11501522,11571025,11331011)；北京市自然科学基金项目(1142003,L140003)；郑州大学青年启动基金项目(1512315004)；郑州大学优秀青年基金项目 (32210452).

胡玉萍(1971—), 女, 河南开封人，副教授，主要从事非参数统计研究，E-mail:hyp@zzu.edu.cn.

O212.7

A

1671-6841(2017)04-0005-06