离散跳变无限不定随机线性二次控制

张志铭， 王文莹

(1.山东科技大学 经济管理学院，山东 青岛 266590；2.山东科技大学 数学与系统科学学院， 山东 青岛 266590)



离散跳变无限不定随机线性二次控制

张志铭1， 王文莹2

(1.山东科技大学 经济管理学院，山东 青岛 266590；2.山东科技大学 数学与系统科学学院， 山东 青岛 266590)

主要论述了伴有状态和控制独立噪音的无限离散时间系统的带马尔科夫跳的随机线性二次控制问题. 该问题给出了一个包含等式和不等式约束的广义代数黎卡提方程(GARE). 跳变不定线性二次控制(LQC)问题的适定性被证明与一个线性矩阵不等式(LMI)的可行性是等价的； 并且GARE一个镇定解的存在性等价于跳变线性二次控制问题的可达性. 最后给出了一个基于LMI的方法通过半定规划来解决GARE.

离散时间系统；马尔科夫跳跃过程；不定随机线性二次控制；广义代数黎卡提方程；半定规划；线性矩阵不等式

1 问题的陈述与准备工作

考虑以下离散时间的带有马尔科夫跳跃过程的随机系统:

x(l+1)=Aθ(l)(l)x(l)+Bθ(l)(l)u(l)+[Cθ(l)(l)x(l)+Dθ(l)(l)u(l)]ωl,l∈N,x0∈Rn.

(1)

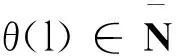
我们指定F(l)是由ω(l)(l∈Ν)生成的σ-代数, 即, F(l)=σ(ω(s):1≤s≤l). 令L2(Ω,Rm)表示满足E‖ξ‖2<的Rm-值随机向量ξ的空间.是由所有的序列y={y(l):y(l)∈Rm}l∈N组成的, 对于l∈N, y(l)∈L2(Ω,Rm)就是F(l-1)可测量的, 在这里我们定义F(-1)也就是说, y0是一个常数. 最后,定义了的l2-范数.

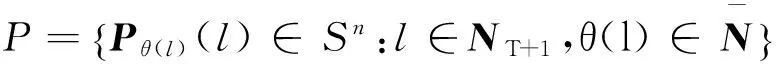
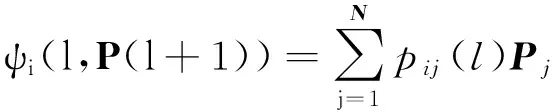
并且我们在后面讨论中令马尔科夫链θ(l)=i, 现给出下面的定义：

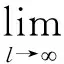
是均方镇定的, 并且Ki(l)是带有马尔科夫跳的适当维数的矩阵, 那么满足u(l)=Ki(l)x(l)的u={u(l)∶l∈N}叫做均方反馈镇定控制.

定义2 如果存在一个均方反馈镇定控制满足u(l)=Ki(l)x(l). 在这里Ki(l)是带有马尔科夫跳的适当维数的矩阵. 那么称系统(1)在均方意义上是镇定的.

对于系统(1), 容许控制集合Uad(x0)定义如下:

对于给定的x0,ul是均方镇定的}.

对任意的(x0,ul)∈Rn×Uad(x0), 关于系统(1)的目标函数定义如下:

(2)

在这里Li(l)∈Rn×m,Qi(l)∈Sn以及Ri(l)∈Sm是给定的带马尔科夫跳的矩阵.

本文线性二次最优控制问题的重点就是要找到一个控制序列u*=(u*(0),…,u*(n),…)∈Uad(x0)满足下列

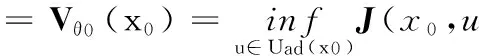
(3)

我们把Vθ0(x0)叫做最优目标值.

定义4 在L∈Sn上

(4)

并且

(5)

满足上述条件的代数方程叫做受约束的GARE.

引理1[2]对任意的矩阵M∈Rm×n, 都会存在一个唯一的矩阵M+∈Rn×m, 使其满足

M+叫做M的广义逆矩阵.

引理2[2]我们给出一个对称矩阵M. 于是就会有

引理3[3]给定矩阵K,M,N, 当且仅当KK+NMM+=N时, 则矩阵方程KXM=N就会有一个解X. 此外, X是由X=K+NM++Y-K+KMM+给出的, 这里的Y是一个带有适当维数的矩阵.

引理4 (舒尔补引理)[4]若具有适当维数的矩阵M=M′,N,R=R′, 则以下条件是等价的:

i)M-NR+N′≥0,R≥0,以及N(I-RR+)=0.

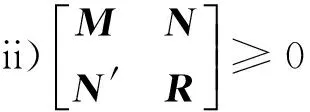
2 广义代数黎卡提方程的充分性

定理1 如果GARE(4)有一个解, 并且存在Yi(l)∈Rm×n和Zi(l)∈Rm满足下面的控制:

(6)

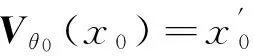
证明 假定L是GARE(4)的一个解. 显然, 当∀T∈N,L∈Sn时, 有

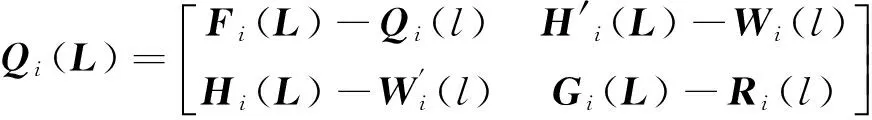
把上述等式添加到性能指标, 我们得到

(7)

定义下面等式

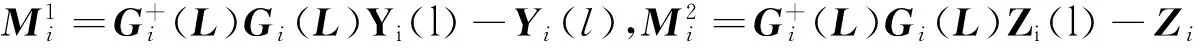
通过配方, 式(7)可以写成

(8)

从而说明以下控制数列

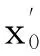
定义5 如果存在一个由公式(6)决定的容许控制, 那么称GARE(4)的一个解L是镇定的.

如果GARE(4)的一个解L是镇定的, 当且仅当对任意x0, 存在Zi(l)∈Rm, 使得控制:

(9)

是容许的, 这里的x(l)是上述控制在初始状态x0下的系统(1)的解.

定义6 如果L≥L*且对任意的L*满足

(10)

通过定义6可知, 如果最大解存在, 那一定是唯一的. 接下来, 我们将讨论GARE(4).

定理2GARE(4)至多有一个镇定解. 而且, 这个镇定解也是它的最大解.

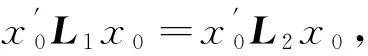
对任何的L*满足式(10)以及GARE(4)的镇定解L. 把L*带入等式(8)中, 可以得到

3 线性二次控制问题的适定性和可达性

引理5 如果LQC问题(1)-(3)是适定的. 当且仅当存在一个对称的常数矩阵Pθ0满足下列等式

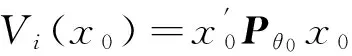
(11)

(12)

添加到下列的目标函数:

然后应用等式(1), 对于任意的(x0,u(l))∈Rn×Uad(x0), 我们可以看出:

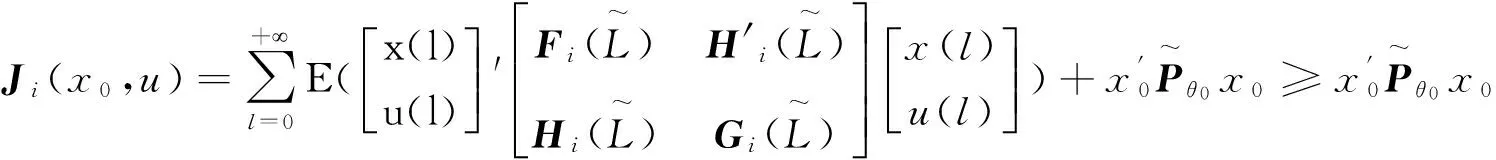
(13)

上述不等式说明了LQC问题的适定性.

通过动态规划原理. 我们得到下列不等式:

基于等式(1)和上述不等式. 我们得出

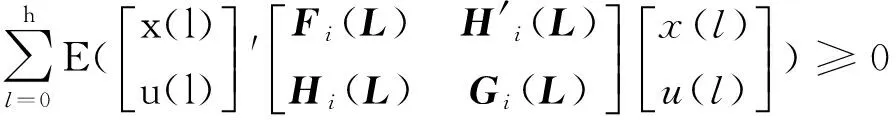
(14)

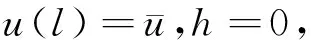
定理4 对于任意的x0,LQC问题(1)-(3)是可达的, 那么GARE(4)就会有一个镇定的解. 而且任意的最优控制都是由等式(6)给出的.

(15)

对任何的初始状态x0, 我们假定u*是一个最优控制. 和定理3一样, 我们得出下列公式:

(16)

接下来, 我们证明了任何最优控制u*(l)均可由公式(6)得出. 通过公式(15), 可以得出

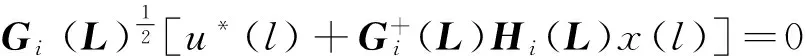
4 通过半定规划表示线性二次控制问题

定义7[5]假设向量c=(c1,…,cm)′∈Rm和矩阵F0,F1,…,Fm∈Sn. 下面最优化问题:

(17)

称之为一个半定规划. 如果存在一个x满足Fi(x)≥0, 则半定规划就是可行的.

考虑下面的半定规划问题:

(18)

下面的定理介绍了LQC问题的适定性, 半定规划的可行性以及GARE三者之间的关系.

定理5 半定规划是可行的, 当且仅当LQC问题(1)-(3)是适定的.

定理7 如果LQC问题(1)-(3)是可达的, 则半定规划(18)的唯一最优解是GARE(4)的镇定解.

5 结束语

本文研究了带有状态和控制独立噪音的离散随机系统的跳变无限不定LQC问题. 文中利用了GARE. 证明了LQC问题的适定性等价于LMI的可行性. 而且,LQC问题的可达性等价于GARE镇定解的存在性. 所有的最优控制都可根据GARE的解来得到. 基本上来说, 本文的结论可以看作是文献[6]一种含马尔科夫跳变系统的版本.

[1]HUANGYL,ZHANGWH,ZHANGHS.Infinitehorizonlinearquadraticoptimalcontrolfordiscrete-timestochasticsystems[J].AsianJournalofControl,2008,10(5):609-615.

[2]PENROSER.Ageneralizedinverseformatrices[J].MathematicalProceedingsoftheCambridgePhilosophicalSociety, 1955, 51(3): 406- 413.

[3]RAMIMA,CHENX,ZHOUXY.Discrete-timeindefiniteLQcontrolwithstateandcontroldependentnoises[J].JournalofGlobalOptimization, 2002, 23(3/4): 245-265.

[4]ALBERTA.Conditionsforpositiveandnonnegativedefinitenessintermsofpseudo-inverse[J].SIAMJournalonAppliedMathematics, 1969, 17(2): 434-440.

[5]VANDENBERGHEL,BOYDS.Semidefiniteprogramming[J].SIAMReview, 1996, 38(1): 49-95.

[6]ZHANGWH,LIY,LIUXK.Infinitehorizonindefinitestochasticlinearquadraticcontrolfordiscrete-timesystems[J].ControlTheoryandTechnology, 2015, 13(3): 230-237.

(编辑：姚佳良)

Infinitehorizon indefinite stochastic LQC for discrete-time Markov jump systems

ZHANG Zhi-ming1，WANG Wen-ying2

(1.College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, China; 2.College of Economics and Management, Shandong University of Science and Technology,Qingdao 266590, China)

This paper primarily discusses discrete-time infinite horizon stochastic linear quadratic control (LQC) problem with state and control dependent noise and Markov jump. The problem provides a generalized algebraic Riccati equation (GARE) that involves equality and inequality constraints. The well-posedness of the indefinite LQC problem with Markov jump is equivalent to the feasibility of a linear matrix inequality (LMI). In addition, the existence of a stabilizing solution to the GARE is equivalent to the attainability of the LQC problem with Markov jump. Definitively, we give an LMI-based approach to figure out the GARE by a semidefinite programming.

discrete-time system; Markov jump; indefinite stochastic LQC; generalized algebraic Riccati equation; semidefinite programming; linear matrix inequality

2016-03-28

张志铭, 男, zhimingzhang1989@163.com; 通信作者：王文莹, 女, wenyingwang1990@163.com

1672-6197(2017)01-0043-06

O231.3

A