r重二元正交多小波的构造

吕 军，石晓煜，轩亚男，陈雅芳，摆 鹏，刘 凯

(新疆农业大学 数理学院, 新疆 乌鲁木齐 830052)



r重二元正交多小波的构造

吕 军，石晓煜，轩亚男，陈雅芳，摆 鹏，刘 凯

(新疆农业大学 数理学院, 新疆 乌鲁木齐 830052)

多小波是小波理论的新发展，研究r重二元正交多小波理论是研究多小波和双向多小波理论必要的奠基性工作.系统给出了相应r重二元正交多小波的构造，讨论了这种小波相应的尺度函数的相关性质，并给出了算例.

r重多小波；正交；多尺度函数

多小波是小波理论的新发展，多小波是指由两个或两个以上的函数作为尺度函数生成的小波，为了区别多小波与传统意义下由一个尺度函数生成的小波，称后者为纯量小波，也称单小波.由于多小波可同时拥有如对称性、短支撑性、正交性和高阶消失矩等许多良好的性质，使得多小波比单一小波具有更多的优势.由于多通道滤波器理论的需要，使得多小波理论在近几年有了迅猛发展.但是多小波的理论发展还有很多问题需要完善,研究r重二元正交多小波理论对研究多小波和双向多小波理论是很有必要的奠基性工作.本文将系统给出相应r重二元正交多小波的构造，讨论这种小波相应的尺度函数的相关性质，并给出算例.

1 r重二元正交多小波的构造

引入L2(R2)r空间上的内积∀f(x,y),g(x,y)∈L2(R2)r.

(1)

而f(x,y)=[f1(x,y),f2(x,y),…,fr(x,y)],g(x,y)=[g1(x,y),g2(x,y),…,gr(x,y)].

定义f(x,y)的Fourier变换

(2)

其逆变换定义为

(3)

设F和G是有限维或可数无限维线性空间.F和G的基底是…,f0,f1,f2,…和…,g0,g1,g2,…，那么以形如figj(i,j=0,±1,±2,…)为基底的空间H，称为F和G的张量积空间，记:H=F⊗G.

{2kφ1(2kx-k1)φ(2ky-k2),2kφ2(2kx-k1)φ(2ky-k2),…,2kφr(2kx-k1)φ(2ky-k2)}

由Φ(x)和φ(y)的两尺度细分方程，我们给出Φ(x,y)的两尺度细分方程.令

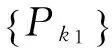
(4)

其中{Pk,k2=Pk1pk2}是Φ((x,y)的r×r两尺度矩阵序列.

对(4)式两端做Fourier变换，可得

(5)

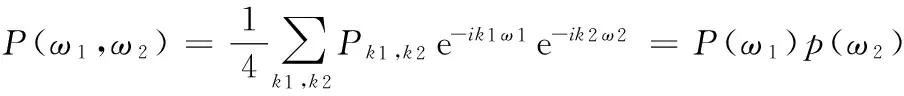
反复应用(5)式可得

(6)

定义1 r重二元多尺度函数向量Φ((x,y)是正交的，若它满足下列等式：

〈Φ((x,y),Φ((x-k1,y-k2)〉=δ0,k1δ0,k2Ir

(7)

定理1 如果Φ((x)和φ(y)是正交的，则由(4)式定义的多尺度函数向量Φ((x,y)也是正交的.

证明 由(4)式及Φ((x)和φ(y)的正交性，得到

对于这种正交张量积的r重二元多尺度函数向量，有

〈Φ((x,y),Φ((x-k1,y-k2)〉=〈Φ((x),Φ((x-k1)〉〈φ(y),φ(y-k2)〉

定理2 如果r重多尺度函数向量Φ((x,y)是由正交的Φ((x)和φ(y)定义的，那么Φ((x,y)的两尺度矩阵符号满足：

(8)

定理3 如果r重多尺度函数向量Φ((x,y)是由正交的Φ((x)和φ(y)定义的，那么Φ((x,y)的两尺度矩阵序列满足

(9)

证明 由上述定理2可知

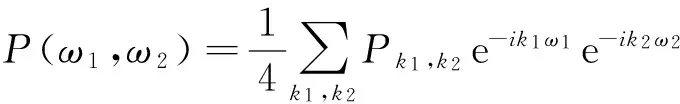
从上述讨论我们知道式(8)与式(9)是等价的，都能表示多尺度函数Φ((x,y)的正交性.

定义2 r重二元多小波Ψ1(x,y)，Ψ2(x,y)和Ψ3(x,y)是正交的，若它满足下列等式：

(10)

其中：i,j=1,2,3.

定理4 如果Φ((x)和Ψ(x)，φ(y)和ψ(y)分别是正交的，则多小波Ψ1(x,y),Ψ2(x,y)和Ψ3(x,y)也是正交的.

定理5 如果r重多尺度函数向量Φ((x,y)对应的多小波Ψ1(x,y)，Ψ2(x,y)和Ψ3(x,y)是由正交的Φ((x)和Ψ(x)，φ(y)和ψ(y)定义的，那么Ψ1(x,y)，Ψ2(x,y)和Ψ3(x,y)的两尺度矩阵符号满足

(11)

定理6 如果r重多尺度函数向量Φ((x,y)对应的多小波Ψ1(x,y)，Ψ2(x,y)和Ψ3(x,y)是由正交的Φ((x)和Ψ(x)，φ(y)和ψ(y)定义的，那么Ψ1(x,y)，Ψ2(x,y)和Ψ3(x,y)的两尺度矩阵序列满足

(12)

从上述讨论知道式(11)与式(12)是等价的.

以上讨论了一种特殊的r重二元张量积多小波，它是基于多分辨分析这个十分重要的工具.我们得到了重要的两尺度方程

(13)

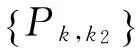
对(13)式两端做Fourier变换，可得

(14)

反复应用(13)式可得

(15)

设两尺度矩阵符号P(ω1,ω2)生成的Φ((x,y)是连续的，且Φ((x,y)的整数平移构成正交系，则1分别是P(0,0)的单特征值，其它的特征值的模都小于1.称此条件为条件E.

下面我们给出多重二元多分辨分析的定义.

Vj=ClosL2(R2)<2jφi(2jx-k1,2jy-k2),i=1,2…,r,k1,k2∈Z>

(16)

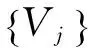
(iii)f(x,y)∈Vj⟺f(2x,2y)∈Vj+1;

(iv) 存在r重二元函数向量Φ((x,y)=[φ1(x-k1,y-k2),…,φr(x-k1,y-k2)]T，使得集合{φi(x-k1,y-k2):i=1,2,…,r,k1,k2∈Z}是V0的Riesz基.即存在正常数A≤B<，使得对于任意系数向量序列有

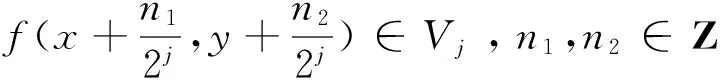
定义Φ(j,k1,k2(x,y):=2jΦ((2jx-k1,2jy-k2)，由多分辨分析定义可知{Φ(j,k1,k2(x,y),k1,k2∈Z}也构成Vj的Riesz基.即

2 算例

例1 给出由C-L多小波和Db2小波构造的张量积小波的2重二元多小波.

C-L多小波：

Db2小波：

则

[1]ALPERTBK.AclassofbasisinL2sparserepresentationofintegraloperators[J].SIAMJMath.Anal,1993,26:246-262.

[2]GOODMANTNT,LEESL.Waveletsofmultiplicityr[J].Trans.Amer.Math.Soc,1994,342(1):307-324.

[3]DONOVANGC,GERONIMOJ,HARDINDP.Constructionoforthogonalwaveletsusingfractalinterpolationfunctions[J].SIAMJMath.Anal,1996,27:1 158-1 192.

[4]CHUICK,LIANJA.Astudyoforthonormalmultiwavelet[J].J.Appl.Number.Math,1996,20(3):273-298.

[5]KWONSG.Two-directmultiwaveletmoments[J].AppliedMathematicsAndComputation.2012,219,(8)：3 530-3 540.

[6] 崔丽鸿.紧支撑的小波、多小波理论及构造[D].西安：西安交通大学,2004.

[7] 杨守志,李尤发.具有高逼近阶和正则性的双向加细函数和双向小波[J].中国科学A辑:数学,2007,37(7):779-795.

[8] 李万社,朱研.双向小波的快速分解和重构算法[J].汕头大学学报(自然科学版),2008,23(4):1-7.

[9] 谢长珍.双向正交的加细函数及其对应双向小波的构造[J].宁夏大学学报,2009,30(1):9-11.

[10]吕卫平.四重正交对称多小波的设计[J].龙岩学院学报,2015(2):8-12.

[11]杨守志,郑贤伟.L2(Rn)上的半正交多小波框架[J].中国科学(数学),2014(3):249-262.

(编辑：郝秀清)

On the construction ofrweight two element orthogonal multi- wavelet

LYU Jun, SHI Xiao-Yu, XUAN Ya-Nan, CHENG Ya-Fang, BAI Peng, LIU Kai

(College of Mathematics and Physics,Xinjiang Agricultural University,Urumqi 830052,China)

Multi-wavelet is the new development of wavelet theory, and study on r weight two element orthogonal multi-wavelet theory is a basic work for the research of multi-wavelet and two-direction multi-wavelet theory. In this paper, we gave the construction of the corresponding r weight two element orthogonal multi-wavelet,discussed on the corresponding properties of the wavelet scale function, and presented examples.

rdimension multi-wavelet; orthogonal; multi scaling function

2016-03-08

新疆农业大学校前期资助课题(XJAU201418)；国家大学生创新训练项目(201510758013)

吕军,男,lvjun136248@sina.com

1672-6197(2017)01-0028-06

O

A