基于Semi-Markov模型的多态系统不完全维修决策

潘刚， 尚朝轩， 蔡金燕， 梁玉英， 孟亚峰,*

1.军械工程学院 电子与光学工程系， 石家庄 050003 2.洛阳电子装备试验中心， 洛阳 471000

基于Semi-Markov模型的多态系统不完全维修决策

潘刚1，2， 尚朝轩1， 蔡金燕1， 梁玉英1， 孟亚峰1,*

1.军械工程学院 电子与光学工程系， 石家庄 050003 2.洛阳电子装备试验中心， 洛阳 471000

为提高复杂多态系统的任务完成能力，降低维修资源消耗，提出了基于Semi-Markov模型的预防性维修和修复性维修相结合的多态系统不完全维修决策方法。采用Semi-Markov模型描述部件的性能衰退过程，利用通用生成函数方法对系统的可靠性指标进行分析，在不完全维修模型基础上，从“系统级维修的角度”出发，提出了预防性维修和修复性维修相结合的不完全维修决策方法，确保系统在有限的服役期内，获得最大净效益。并以某航空发动机压气机子系统的维修决策为例进行分析，该方法可以有效的结合预防性维修和修复性维修的优势，提高了系统的任务完成能力，具有很强的通用性和工程应用价值。

多态系统； Semi-Markov模型； 预防性维修； 修复性维修； 维修决策

大型复杂装备系统中广泛存在着多态(多状态)可修系统，当前，多态系统主要分为两类：多工作(失效)状态系统和多性能水平系统。多工作(失效)状态系统是指系统除了“正常工作”和“完全失效”两种状态外，还具有多种工作(或失效)状态[1]。例如，在航空航天领域中常用的k/n(G)系统就是典型的多工作(失效)状态系统。多性能水平系统是指系统可以在多种性能水平下运行。例如，对于一个300 MW的发电机组，当完全正常时，其发电水平为300 MW，当通风机或粉碎机发生故障时，会使得发电机组的发电水平降低，可能为150、200、225 MW等[1-2]。性能退化系统在工作时可呈现多种性能水平，也是一种典型的多性能水平系统。例如，航空发动机随着工作时间的积累，由于自然磨损、疲劳、腐蚀以及积垢或维修管理不当等原因，部分部件的性能会出现退化，整个系统的技术状态呈现下降的趋势，具有多种性能水平[3]。本文将针对退化型多态系统的相关维修决策问题进行研究。对于性能退化系统，会因系统中部件的失效或性能退化而由性能高的状态向性能低的状态演变，倘若整个系统的性能不能满足最小任务性能需求水平，则可认为系统失效[4]。对复杂多态系统的维修决策进行研究，有助于揭示系统退化和维修措施对系统状态性能影响的潜在规律，从而制定更加合理、高效、经济的维修计划。

多态系统的维修决策研究首先由Levitin和Lisnianski[5]提出，而后引起学者们的广泛研究。从维修效果的角度来分析，针对复杂多态系统的维修决策研究主要分为两类：一是基于“完好维修”和“最小维修”假设的多态系统冗余和维修决策研究[5-7]；二是基于“不完全完好维修”假设的多态系统维修决策分析[8-13]。从维修方式的角度来分析，针对多态系统的维修决策研究主要分为3类：一是多态系统预防性维修决策研究[8,13-17]；二是多态系统修复性维修更换决策研究[10-11]；三是预防性和修复性维修相结合的多态系统维修决策研究[18-19]。由上述研究不难发现，关于多态系统的维修决策研究从维修效果的角度分析经历了由理想的“完好维修”和“最小维修”假设，到更贴近实际的介于“完好维修”和“最小维修”之间的“不完全维修”假设；从维修方式的角度分析经历了单一预防性维修、修复性维修到预防性和修复性维修相结合的维修方式。鉴于此，对当前关于“不完全完好维修”、预防性维修与修复性维修相结合的相关成果进行分析。文献[8]首次从“系统级角度”采用随机恢复因子模型对多态系统的维修决策进行研究。以文献[8]为基础，Liu和Huang[12]针对其可能存在的不足，假设随着维修次数的增加，部件的状态转移率成比例的增加，并以准更新过程理论进行描述，此外将部件的退化规律用非齐次连续时间马尔可夫模型进行描述。当系统的性能低于最小任务需求时，将系统视为失效，并立即采取修复措施以修复系统中的所有部件。文献[19]假设多态系统在有限寿命周期内同时遭受退化损伤和冲击损伤，以此为基础，采用Markov模型描述多态系统的性能退化过程，研究了多态系统的预防性和最小修复性更换维修策略。实际工程中，科学及时地对多态系统进行维修，可以有效的降低系统失效所带来的运行风险，同时可减少非计划拆换维修所带来的资源浪费。对于多态系统，当其性能低于任务性能需求时，系统被认为失效，立即对其进行修复性维修。此外，为了避免失效的发生，并保证多态系统以较好的性能正常运行，根据多态系统的状态性能水平，需对其进行预防性维修(视情维修)。因此，在多态系统的维修决策中，将系统的修复性维修和预防性维修有效的结合对保证系统的可靠性，合理的确定维修时机、优化维修费用，有着重要的工程价值和经济意义。然而，预防性和修复性维修相结合的不完全维修方面的研究相对较少；此外在对部件状态演变描述方面，多态部件任意状态之间的转移时间并一定服从指数分布，因此，采用Markov过程描述部件或系统的状态转移过程并不恰当。鉴于此，本文针对多态系统在有限服役时间内可能存在具有退化失效和泊松(突发)失效的情况，假定部件在某状态的驻留时间服从Weibull分布，采用Semi-Markov过程描述部件之间的状态转移，并以不完全维修为基础，结合预防性维修和修复性维修的优势，提出了基于Semi-Markov模型的预防性和修复性维修相结合的多态系统不完全维修决策方法，并以实例对本文所提的决策方法进行验证说明。

1 模型描述

1.1 基本假设

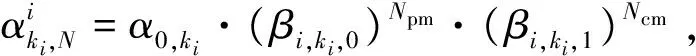
1.2 退化型多状态部件描述

由于部件状态之间的转移时间可能为任意分布，而不单是简单的指数分布，从而限制了Markov 模型的适用性。而半Semi-Markov模型则不要求状态之间的转移时间服从指数分布，可为Weibull等一些常用分布[20-22]，因此，本文选取Semi-Markov模型来描述部件的状态转移过程。

1.2.1 基于Semi-Markov模型的状态概率模型

实际中，部件i可能存在退化失效和突发失效两种失效模式，假定任意时刻(t≥0)，部件i可能具有的状态为{mi,…，ki,…,1}，分别对应状态性能为{gmi,…，gki,…,g1}，部件的性能变化可用连续时间离散状态随机过程gi∈{gmi,…，gki,…,g1}来描述。部件的状态转移过程如图1所示。

假定部件i的初始状态为mi，(初始时刻t=0)令Tκ为完成第κ次转移的时刻，如果对所有κ以及ji,ki∈{1,2,…,mi}有

Qjiki(t)=Pr{Gi(Tκ+1)=gi,ki,Tκ+1-Tκ≤t|

Gi(Tκ)=gi,ji}

(1)

则随机过程{Gi(t),Tκ}为Markov更新过程，Qi(t)为Semi-Markov过程定义的核矩阵，Qi(t)=[Qjiki(t)]。πmiki(t)为部件由初始时刻(t=0)处于状态mi开始，至时刻t(t>0)时转移至状态ki的概率，则概率πmiki(t)可通过求解以下积分方程得到[20-22]

πmiki(t)=δmiki[1-Fmi(t)]+

(2)

图1 多态部件的状态转移过程
Fig.1 State-space diagram of multi-state component

其中：τ(0≤τ≤t)为时间变量；qmili(τ)为Qmili(τ)的微分，代表转移概率函数Qmili(τ)在τ时刻的转移速率；δmiki为指示函数；Fmi(t)为部件i在状态mi驻留时间的非条件概率分布函数，表示在t时刻系统将要离开状态mi的概率。

式(2)是Semi-Markov理论中的主要方程，在给定核矩阵Qi(t)和初始状态的条件下，可求得Semi-Markov过程的所有状态概率πmiki(t)。因πmiki(t)表示部件i在t时刻(t>0)状态性能为ki时的概率[20]，故可令pki=πmiki(t)。

1.2.2 核矩阵的求解

为了得到描述部件i状态变化时Semi-Markov过程的核矩阵Qi(t)，将部件的状态转移看作一个事件，假定对于某类事件，其发生时间间隔的概率分布函数是已知的，转移的实现关键在于诸多事件在竞争中哪一事件最先发生[21-22]。

Qmi,mi-1=Pr{(Tmi,mi-1≤t)&

(Tmi,mi-2>t)…&(Tmi,1>t)}=

图2 Semi-Markov过程状态图空间
Fig.2 State-space diagram of Semi-Markov process

dFmi,mi-1(τ)

Qmi,mi-2=Pr{(Tmi,mi-1>t)&(Tmi,mi-2≤t)…&

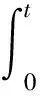
[1-Fmi,1(τ)]dFmi,mi-2(τ)

⋮

Qmi,1=Pr{(Tmi,mi-1>t)&

(Tmi,mi-2>t)…&(Tmi,1≤t)}=

[1-Fmi,mi-2(τ)]dFmi,1(τ)

最终可得到部件i的核矩阵为

1.3 退化型多态系统描述

1) 某全新系统在t=0时刻首次投入使用，计划服役时间为Tend，即当系统的工作时间超过Tend时被全新系统替换。

2) 系统可能有多个退化过程，即其可由“完好性能”状态到“完全失效”状态离散成Ms个离散性能水平状态，“完好性能”状态Ms的性能为gMs，“完全失效”状态1的性能为0，中间状态k的性能为gk，其中，1

3) 系统当前的性能水平，可通过监测到的性能参数进行描述，且监测时间为可忽略的。

4) 假定系统的最小任务性能需求为w，当系统的性能水平低于最小任务性能需求w时，系统不满足任务需求，认为系统失效。

图3 多态系统的状态转移过程
Fig.3 State-space diagram of multi-state system

2 多态系统可靠性指标分析

2.1 部件状态性能定义

定义部件i在状态ki时的状态性能为gi,ki，其表示部件i处于不同性能参数水平时对整个系统正常工作性能的贡献比率，在此以百分比进行表示。通常结合系统结构与部件的性能参数进行定义，可分为以下3种情况：

1) 部件处于不同状态时对整个系统正常工作性能的贡献比率可准确定量时，根据部件处于不同状态时对整个系统正常工作性能的贡献比率，直接对部件的状态性能进行划分。

2) 部件处于不同状态时对整个系统正常工作性能的贡献比率可近似定量时，根据部件处于不同状态时对整个系统正常工作性能的贡献比率，近似对部件的状态性能进行划分。

3) 对于一些复杂的特殊情况，部件处于不同状态时对整个系统正常工作性能的贡献比率无法定量时，可将该部件与其他相邻部件构成的分系统看作为“部件”，然后再结合式(1)、式(2)对“部件”的状态性能进行划分。

采用Semi-Markov模型得到部件的状态概率之后，根据系统的结构函数，利用通用生成函数(UGF)方法对系统的可靠性指标进行分析。

2.2 运算法则

假定部件i在第N个正常运行周期内的通用生成函数为[21-22]

(3)

式中：gN,ki为部件i在第N个正常运行周期内状态为ki时的状态性能；pN,ki(t)为t时刻部件i的状态性能为gN,ki时对应的状态概率；i=1,2,…,n，ki=1,2,…,mN,i，n为系统中部件的个数；mN,i为部件i在第N个正常运行周期内的状态个数。

假定系统的通用生成函数可通过如下运算获得：

UN(z,t)=Ω(uN,i(z,t),uN,i′(z,t))=

根据系统结构特点定义如下运算符：

1) 当gN,ks为gN,ki与gN,ki′的和时，定义δ1运算符为

δ1(uN,i(z,t),uN,i′(z,t))=

2) 当gN,ks为gN,ki与gN,ki′的最小值时，定义δ2运算符为

δ2(uN,i(z,t),uN,i′(z,t))=

2.3 多态系统平均瞬态性能分析

对系统进行维修的关键在于对系统的状态性能进行分析，即当系统的平均瞬态性能小于最小任务性能需求w或某维修阈值时，将对系统采取维修措施。因此对系统的平均瞬态性能分析具有重要意义，在此，采用状态性能的期望来描述多态系统的平均瞬态性能(简称：平均性能)，具体如下所述。

定义多态系统t时刻在第N个正常运行周期内的平均瞬态性能大小为[21]

(4)

式中：gN,ks(t)为t时刻系统在第N个正常运行周期内第ks个状态的状态性能；pN,ks(t)为t时刻系统在第N个运行周期内状态性能为gN,ks(t)时对应的状态概率，ks∈{MN,s,…，2,1},1≤N≤N*。

2.4 基于UGF的系统可靠性分析

据上述运算法则的分析，假定多态系统在第N个正常运行周期内的通用生成函数为

(5)

定义多态系统的最小任务性能需求为w，则系统在第N个运行周期内的可靠度为

RN(t)=P{GN(t)≥w}=

(6)

式中：1(gN,ks(t)-w≥0)为示性函数；当gN,ks(t)-w≥0时，1(gN,ks(t)-w≥0)=1；当gN,ks(t)-w<0时，1(gN,ks(t)-w≥0)=0，GN(t)={gN,Ms(t),…,gN,ks(t),…,gN,1(t)}。

系统在第N个运行周期内，进行第Npm次预防性维修时系统的平均正常运转时间为

(7)

式中：kNpm为系统采取预防性维修时系统所处状态。

系统在第N个运行周期内，进行第Ncm次修复性维修时系统的平均正常运转时间为

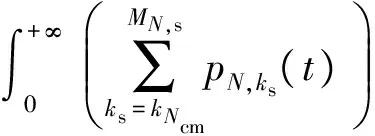
(8)

式中：kNcm为系统采取修复性维修时系统所处状态。

3 多态系统的维修决策模型

3.1 模型假设

在对多态系统的维修决策分析之前，首先对系统做如下假设：

1) 假定多态系统中各部件经过维修后均能恢复到其最好性能状态，但并非完全修复如新。在下一个维修周期内，被修复后的部件从高性能状态衰退到低性能状态的速率变快，换言之，部件的状态转移率将呈比例增长[12]。

2) 假定系统为多个退化型部件以任意的物理连接构成，且系统在任意时刻的状态概率分布ps(t)可通过1.2节Semi-Markov模型和通用生成函数法计算得到。

3) 假定对系统进行预防性维修时，单位时间内所需的费用要小于修复性维修，且所需平均维修时间要低于修复性维修，但是预防性维修的维修效果要比修复性维修差。

5) 假定系统在第N次维修的平均修复时间服从概率密度函数为f(t,αN,λN)=λN·αN(λN·t)αN-1exp(-λN·t)αN，分布函数为F(t,αN,λN)=1-exp(-λN·t)αN的Weibull分布。其中：t≥0,αN,λN>0且分别为形状参数、尺度参数，且分布参数可以通过对维修记录和专家经验知识进行统计分析得到。

6) 假定系统在第N次维修所需时间的分布参数满足如下关系：

αN=(αpm0)ψ(N)·(αcm0)1-ψ(N)·βpmNpm·βcmNcm

λN=(λpm0)ψ(N)·(λcm0)1-ψ(N)·γpmNpm·γcmNcm

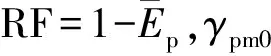
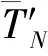
3.2 维修决策目标

1) 令Cw、Cpm、Ccm、Cr分别为单位时间内的系统产生的报酬、单位时间的预防性维修费用、单位时间的修复性维修费用、以及系统的固定购置费用，一般认为Cpm,Ccm≪Cr。

(9)

(10)

3.3 维修决策变量

3.4 维修决策模型分析

基于上述分析，给出如下维修决策分析步骤。

步骤1根据1.2.1节Semi-Markov模型的状态概率求解方法，求解部件的状态概率，并用通用生成函数方法对部件的状态概率分布进行表示。

步骤2由部件的通用生成函数，根据2.1节定义通用生成函数运算法则，求得分系统、系统有关通用生成函数的状态概率分布表示。

步骤3根据2.2节和2.3节求得多态系统的系统可靠度和平均瞬态性能，同时根据式(7)和式(8)求得系统在第N个运行周期内，实施第Npm次预防性维修和第Ncm次修复性维修时系统正常运转的时间。

步骤4根据3.1节假设5)～7)求得对系统进行预防性维修和修复性维修的平均时间。

步骤5由3.1节模型假设3)可知，仅依赖于系统状态性能对其进行维修决策并不是最佳的，因为预防性维修的维修效果相对较差，在某一运行周期内当系统采用预防性维修时，所需的维修时间和维修费用相对较低，但是其正常运行时间可能相对较低。因此，在步骤1～4的基础上，作如下分析：

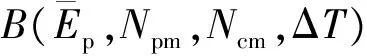
3.5 模型适应性分析

当系统的维修决策满足如下条件时，可采用本文所提维修决策模型对其进行维修决策分析。

1) 维修决策应用的对象为退化型多态系统。

2) 系统的服役时间为有限的。

3) 维修后部件并非处于全新状态，满足非完好维修模型，认为部件经过维修后恢复到其最高性能状态，但是在下一维修周期内，部件的衰退速度加快[4]。

4) 系统在服役期间内开展维修活动时，根据实际工程需求，需要采用修复性维修和预防性维修两种维修方式。

4 算例分析

采用文献[1]实例，将所提决策模型应用到航空发动机压气机子系统的更换维修决策问题中。根据压气机子系统的基本工作原理和组成结构，可用图4所示的可靠性框图表示压气机子系统。性能状态退化部件1和2分别代表了压气机子系统的一级转子和二级转子，主要实现进气和提高空气压力的功能；退化型部件3表示压气机子系统的静子，其主要组成部分包括机匣和整流器，它将辅助转子实现压气功能。因此，整个压气机系统的进气压气效率将由静子和两级转子共同决定。性能水平(%)如图4所示，部件1的性能水平分别为g1,2=35%、g1,1=0%，部件2的性能水平分别为g2,2=65%、g2,1=0%，部件3的性能水平分别为g3,3=100%、g3,2=50%和g3,1=0%。

图4 压气机子系统的结构
Fig.4 Structure of compressor subsystem

表1给出了系统中各部件在第一个维修周期内的在状态驻留分布函数参数，部件的各状态性能及对应的非完好维修的比例参数。其中，部件的性能水平表示为部件处于不同状态时对整个压气机子系统正常工作性能的贡献比率。表2和表3 分别给出维修模型参数和费用相关参数。

表1 退化部件参数Table 1 Degraded component’ parameters

表2 维修模型参数Table 2 Maintenance model parameters

表3 费用相关参数Table 3 Maintenance model parameters 万元

4.1 部件和系统的状态性能及概率分布

4.1.1 部件状态性能及概率分布

现以第一个正常运行周期内的维修决策为例进行说明。根据1.2.1节状态概率求解方法，求解各部件的状态及状态概率，由图4可知，部件1、2具有两个状态，部件3具有3个状态，首选对部件的状态概率求解过程进行分析。

则，核矩阵有

由式(2)可得部件3的状态为

同理可得部件2和部件1的状态概率具体为

1) 部件2

2) 部件1

4.1.2 系统的状态性能及概率分布

在得到系统内各部件的状态概率及状态性能之后，根据2.2节定义的δ1和δ2运算符，对系统的状态概率和状态性能进行求解，结果如下。

4.2 多态系统可靠性指标分析

4.2.1 多态系统的平均瞬态性能

多态系统t时刻在第N个正常运行周期内的平均瞬态性能大小为

通过对图5分析可得出的如下结论：

1) 随着维修次数的增加，系统的平均瞬态性能的退化趋势加快，即执行任务的能力逐渐降低。

2) 在有限服役期内，仅采取预防性维修要比仅采取修复性维修的次数要多，且随着预防性维修次数的增加，系统可正常工作的时间减少的更加明显，其主要是由于预防性维修的维修效果相对较差引起的。

图5 系统平均瞬态性能与维修间隔的关系
Fig.5 Relationship between system mean instantaneous performance and maintenance interval

4.2.2 多态系统的可靠性

假定多态系统的最小任务性能需求为50%，则系统在第N个运行周期内的可靠度为

RN(t)=P{GN(t)≥50%}=

通过对图6分析可得出的如下结论：

1) 随着维修次数的增加，系统到达维修阈值时的可靠度呈降低的趋势，同时，系统的可靠度的降低速率呈增大的趋势，究其原因是由于对系统的不完全维修造成的。

2) 随着时间的推移，对系统的维修次数不断增加，不难发现，采取预防性维修时，系统可靠度下降速率要比采取修复性维修时快。

图6 系统可靠度与维修间隔的关系
Fig.6 Relationship between system reliability and
maintenance interval

4.3 维修决策模型变量灵敏度分析

表4系统净效益与决策模型变量间的关系

Table4Relationofsystemnetbenefitanddecision-markingmodelvariables

EpΔT/monthNpmNcmB(E∗p，N∗pm，N∗cm，ΔT∗)/万元0．510．6103963．70．510．7103963．70．510．8103963．70．510．9132975．10．511．0132975．10．511．1132975．10．511．2161946．10．511．3161946．10．511．4161946．10．511．5210915．60．511．6210915．60．520．684960．50．520．7103964．20．520．8103964．20．520．9103964．20．521．0132966．10．521．1132966．10．521．2132966．10．521．3171955．60．521．4171955．60．521．5171955．60．521．6171955．60．530．694969．80．530．794969．80．530．8113973．10．530．9113973．10．531．0113973．10．531．1132957．70．531．2132957．70．531．3132957．7

续表

续表

通过对表4分析可得出如下结论：

3) 分析时间决策阈值ΔT*的选取对系统净效益的影响，时间决策阈值ΔT*的取值较大时，系统在决策上更加倾向于预防性维修，此时对系统的预防性维修次数会随着ΔT*取值增大而增加，反之修复性维修次数会随着ΔT*取值减小而减少。

4.4 多态系统的维修决策

说明：图7～图10中，方法1为采用预防性维修与修复性维修相结合的维修方式，方法2为采用预防性维修，方法3为修复性维修。

图7 系统净效益与维修方式的关系
Fig.7 Relation of system net benefit and maintenance methods

通过对图7分析可得出的如下结论：

1) 采用预防性维修与修复性维修相结合的维修方式的最大净效益点为(13,2,975.1)，即按图9维修顺序，经过12次预防性维修、2次修复性维修后系统的净效益为975.1万元。

2) 仅采用预防性维修的最大净效益点为(21,0,915.6)，即采用21次预防性维修后系统的净效益为915.6万元。

3) 仅采用修复性维修的最大净效益点为(0,9,949.5)，即采用9次修复性维修后系统的净效益为949.5万元。

系统在总服役时间Tend=120 month内的净效益与维修时间间隔的变化关系如图8所示。

对图7和图8分析可得出的如下结论：

3) 采用修复性维修的维修时刻分别为{16.70,32.67, 47.93, 62.53, 76.51, 89.89, 102.73, 115.04}。

图8 系统净效益与维修间隔的关系
Fig.8 Relation of system net benefit and maintenance interval

4) 由1)～3)分析可知，采用预防性维修与修复性维修相结合的维修方式在规定服役期间内所得净效益最大，由于采用视情维修与事后维修相结合的维修方式是对视情维修与事后维修优势的结合，进一步说明了预防性维修与修复性维修相结合的维修方式要优于其他的两种维修方式。

系统在总服役时间Tend=120 month内的维修费用与维修方式的变化关系具体如图9所示。

系统在总服役时间Tend=120 month内的维修费用与维修时间间隔的变化关系具体如下图10 所示。

通过对图9和图10分析可得出的如下结论：

1) 采用预防性维修与修复性维修相结合的维修方式在完成12次预防性维修、2次修复性维修后系统还能正常使用时系统已到达最高服役时间，且最大维修费用为3.251 7万元。

图9 系统维修费用与维修方式的关系
Fig.9 Relation of system costs and maintenance
methods

图10 系统维修费用与维修间隔的关系
Fig.10 Relation of system costs and maintenance interval

2) 采用21次预防性维修后系统的最大维修费用为3.366 5万元。

3) 采用8次修复性维修后系统的最大维修费用为6.215 0万元。

4) 由1)～3)可知，系统服役年限到达后与其他两种维修方式相比，采用预防性维修与修复性维修相结合的维修方式所需的维修费用最少。

5 结 论

为提高装备系统的任务执行能力，提出了一种提出了基于Semi-Markov模型的预防性和修复性维修相结合的多态系统不完全维修决策方法。

1) 该方法采用Semi-Markov模型描述部件的退化过程，克服了Markov模型状态驻留时间只能为指数分布的不足，提高了求解部件状态概率的精度。

2) 通过分别对预防性维修和修复性维修下系统的平均瞬态性能和可靠度进行分析，可知由于对系统的不完全维修，导致系统执行任务的能力随着维修次数的增加而逐渐降低。

3) 充分结合预防性维修和修复性维修的优势，制定了更加高效合理的维修决策方案，提高了装备系统的任务执行能力。

[1] 李春洋. 基于多态系统理论的可靠性分析与优化设计方法研究[D]. 长沙: 国防科学技术大学, 2010: 2-5.

LI C Y. Research on reliability analysis and optimization based on the multi-state system theory[D]. Changsha: National University of Defense Technology, 2010: 2-5 (in Chinese).

[2] TIAN Z G. Multi-state system reliability analysis and optimization[D]. Alberta: University of Alberta, 2007: 3-4.

[3] 任淑红. 民航发动机性能可靠性评估与在翼寿命预测方法研究[D]. 南京： 南京航空航天大学, 2010: 2-4.

REN S H. Research on methods of performance reliability assessments and life on wing prediction for civil aeroengine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010: 2-4 (in Chinese).

[4] 刘宇. 多状态复杂系统可靠性建模及维修决策[D]. 成都: 电子科技大学, 2011: 48-68.

LIU Y. Multi-State complex system reliability modeling and maintenance decision[D]. Chengdu: University of Electronic Science and Technology of China, 2011: 48-68 (in Chinese).

[5] LEVITIN G, LISNIANSKI A. Joint redundancy and maintenance optimization for multistate series-parallel systems[J]. Reliability Engineering and System Safety, 1999, 64(1):33-42.

[6] MUSTAPHA N, DAOUD A K. Optimization of series-parallel multi-state systems under maintenance policies[J]. Reliability Engineering and System Safety, 2007, 92(12):1620-1626.

[7] NOURELFATH M, DUTUIT Y. A combined approach to solve the redundancy optimization problem for multi-state systems under repair policies[J]. Reliability Engineering and System Safety, 2004, 86(3): 205-213.

[8] CHER M T, NAGARAJAN R. A framework to practical predictive maintenance modeling for multi-state systems[J]. Reliability Engineering and System Safety, 2008, 93(8): 1138-1150.

[9] CHER M T, NAGARAJAN R. Imperfect predictive maintenance model for multi-state systems with multiple failure modes and element failure dependency[C]//Prognostics & System Health Management Conference, 2010.

[10] 狄鹏, 黎放, 陈童. N型更换策略下多状态可修系统可靠性规律研究[J]. 系统工程与电子技术, 2014, 36(3): 603-607.

DI P, LI F, CHEN T. Research for the reliability of multi-state repairable system with replacement policy[J]. Systems Engineering and Electronics, 2014, 36(3): 603-607 (in Chinese).

[11] 成国庆, 李玲, 唐应辉. 多态退化串联可修系统的最优维修更换策略[J]. 系统工程理论与实践, 2012, 32(5): 1118-1123.

CHENG G Q, LI L, TANG Y H. Optimal replacement policy for a deteriorating series repairable system with multi-state[J]. Systems Engineering—Theory & Practice, 2012, 32(5): 1118-1123 (in Chinese).

[12] LIU Y, HUANG H Z. Optimal replacement policy for multi-state system under imperfect maintenance[J]. IEEE Transactions on Reliability, 2010, 59(3): 483-495.

[13] 葛恩顺, 李庆民, 张光宇, 等. 考虑不完全维修的劣化系统最优视情维修策略[J]. 航空学报, 2013, 34(2): 316-324.

GE N S, LI Q M, ZHANG G Y, et al. Optimization of condition-based maintenance for degradation systems under imperfect maintenance[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 316-324 (in Chinese).

[14] 黄傲林, 李庆民, 黎铁冰, 等. 劣化系统周期预防性维修策略的优化[J]. 系统工程与电子技术, 2014, 36(6): 1103-1107.

HUANG A L, LI Q M, LI T B. Optimization of periodic preventive maintenance policies for deteriorating repairable system[J]. Systems Engineering and Electronics, 2014, 36(6): 1103-1107 (in Chinese).

[15] HUANG C C, YUAN J. A two-stage preventive maintenance policy for a multi-state deterioration system[J]. Reliability Engineering and System Safety, 2010, 95(11): 1255-1260.

[16] 李大伟, 张志华, 钟强晖, 等. 复杂退化系统的组合维修策略优化[J]. 航空学报, 2015, 36(3): 872-880.

LI D W, ZHANG Z H, ZHONG Q H, et al. Optimal combination maintenance strategy of deteriorating complex system[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 872-880 (in Chinese).

[17] 葛小凯, 胡剑波, 张博锋. 考虑依赖性的多部件系统状态维修优化仿真建模[J]. 航空学报, 2013, 34(8): 1854-1863.

GE X K, HU J B, ZHANG B F. Simulation modeling for condition based maintenance optimization of multi-component systems with dependencies[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1854-1863 (in Chinese).

[18] ISAAC W S, MUSTAPHA N, DAOUD A. Performance evaluation of multi-state degraded systems with minimal repairs and imperfect preventive maintenance[J]. Reliability Engineering and System Safety, 2010, 95(2): 65-69.

[19] WU J, NG T S A, XIE M, et al. Analysis of maintenance policies for finite life-cycle multi-state systems[J]. Computers and Industrial Engineering, 2010, 59(4): 638-646.

[20] 尚彦龙, 蔡琦, 赵新文, 等. 基于UGF和Semi-Markov方法的反应堆泵机组多状态可靠性分析[J]. 核动力工程, 2012(1):117-123.

SHANG Y L, CAI Q, ZHAO X W, et al .Multi-state reliability for pump group in nuclear power system based on UGF and Semi-Markov process[J]. Nuclear Power Engineering, 2012(1): 117-123 (in Chinese).

[21] LISNIANSKI A, FRENKEL I, DING Y. Multi-state system reliability analysis and optimization for engineers and industrial managers[M]. London: Springer, 2010.

[22] LISNIANSKI A, LEVITIN G. Multi-state system reliability: assessment, optimization and applications[M]. Singapore: World Scientific, 2003: 155-163.

[23] 曹晋华, 程侃. 可靠性数学引论[M]. 北京: 高等教育出版社, 2006： 15-16.

CAO J H, CHENG K. Introduction to the reliability mathematics[M]. Beijing: Higher Education Press, 2006:15-16 (in Chinese).

[24] 茆诗松, 王玲玲. 加速寿命试验[M]. 北京: 科学出版社, 1997: 9-12.

MAO S S， WANG L L. Accelerated life test[M]. Beijing: Science Press, 1997: 9-12 (in Chinese).

(责任编辑： 苏磊)

URL：www.cnki.net/kcms/detail/11.1929.V.20161104.1506.002.html

Imperfectmaintenancedecisionformulti-statesystembasedonSemi-Markovmodel

PANGang1,2,SHANGChaoxuan1,CAIJinyan1，LIANGYuying1,MENGYafeng1,*

1.DepartmentofElectronicandOpticEngineering,OrdnanceEngineeringCollege,Shijiazhuang050003,China2.LuoyangElectronicsEquipmentTestCenter,Luoyang471000,China

Inordertoimprovethemissioncompletioncapabilityofcomplexmulti-statesystem,reducingmaintenanceresourceconsumption,amaintenancedecisionmethodformulti-statesystembasedonSemi-Markovmodelwereprovided,usingSemi-Markovmodeldescribesthedegradationprocessofcomponents，theuniversalgeneratingfunctionwasusedtoanalyzethereliabilityindicatorofsystem.Basedupontheimperfectmaintenancedecisionmodel,from“theperspectiveofsystemmaintenance”,animperfectmaintenancedecisionmethodisproposedcombinedpreventivemaintenancewithcorrectivemaintenance,ensurethatthesystemobtainsmaximumnetbenefitinthelimitedserviceperiod.andverificationandillustrationareconductedwithaero-enginecompressorsubsystem.Thismethodcaneffectivelycombinepreventivemaintenanceandcorrectivemaintenanceadvantages,enhancesthemissioncompletioncapabilityofsystem,andhasastrongversatilityandengineeringapplicationvalue.

multi-statesystem;Semi-Markovmodel;preventivemaintenance;correctivemaintenance;maintenancedecision

2016-03-02；Revised2016-03-23；Accepted2016-06-13；Publishedonline2016-11-041506

s：NationalNaturalScienceFoundationofChina(61271153,61372039)

.E-mailmyfrad@163.com

2016-03-02；退修日期2016-03-23；录用日期2016-06-13； < class="emphasis_bold">网络出版时间

时间：2016-11-041506

www.cnki.net/kcms/detail/11.1929.V.20161104.1506.002.html

国家自然科学基金 (61271153,61372039)

.E-mailmyfrad@163.com

潘刚， 尚朝轩， 蔡金燕， 等． 基于Semi-Markov模型的多态系统不完全维修决策J． 航空学报,2017,38(2):320178.PANG,SHANGCX,CAIJY,etal.Imperfectmaintenancedecisionformulti-statesystembasedonSemi-MarkovmodelJ.ActaAeronauticaetAstronauticaSinica,2017,38(2):320178.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0189

V233; TB114.3

A

1000-6893(2017)02-320178-15