两级动叶可调式轴流风机前后级异常叶片干涉现象的研究

封 遥， 董云山， 司风琪， 白德龙， 解冠宇

(1. 东南大学 能源热转换及其过程测控教育部重点实验室， 南京 210096；2. 内蒙古岱海发电有限责任公司， 内蒙古乌兰察布 012000)

研究与分析

两级动叶可调式轴流风机前后级异常叶片干涉现象的研究

封 遥1， 董云山1， 司风琪1， 白德龙2， 解冠宇2

(1. 东南大学 能源热转换及其过程测控教育部重点实验室， 南京 210096；2. 内蒙古岱海发电有限责任公司， 内蒙古乌兰察布 012000)

针对某电厂SAF 36-25-2两级动叶可调式轴流引风机，借助Fluent研究了引风机前后级动叶片发生不同角度异常偏离时，风机性能参数的变化规律及前后两级异常叶片的相互干涉关系。研究结果表明：第二级异常叶片偏离角度Δβ2=+8°时风机整体性能要优于Δβ2=-8°时风机性能；保持Δβ2不变，随着第一级异常叶片偏离角度Δβ1从-12°增加到+12°，风机整体性能呈现先增大后减小的变化趋势，且在Δβ1=-12°时风机全压和效率在全流量范围内恶化最为明显，异常叶片对风机性能影响最大，而Δβ1=+8°时异常叶片对风机性能影响最小；第一级异常叶片对第二级叶轮性能的干涉影响随异常叶片偏离程度的增大而增强。

轴流引风机； 动叶； 安装角； 性能特征

风机作为电厂中重要的辅机设备之一，主要应用于制粉系统、燃烧系统、风烟系统及仪器辅用等方面，其可靠性对电厂运行的安全性和经济性有着重要的影响。随着火电机组单机容量的不断提高，实际工程中越来越多地用到了动叶可调式轴流风机，其具有调节范围广、变工况性能好、能源利用率高等众多优点。但是，动叶可调式轴流风机在实际运行过程中，动叶片常常会因为加工安装不规范、滑块磨损、叶柄积灰等问题造成风机叶片卡涩，在动叶调整过程中出现一个或多个叶片安装角异常偏离，造成风机性能下降、不稳定工作区增大，稍有扰动甚至会引发风机的喘振和抢风[1-4]。因此，国内外研究学者围绕轴流风机的叶片断裂、风机振动、失速喘振及内流特征、噪声等方面开展了较多的研究[5-10]。

由于火电机组动叶可调式轴流风机体积庞大，难以采用试验的方法进行风机的性能研究，因而越来越多的学者采用CFD数值模拟方法来研究风机的性能特征及内部流动特征。针对单级轴流风机，黄超[11]针对某火电厂脱硫增压风机，模拟研究了不同转速及安装角的风机性能及流动特性。李春曦等[12]应用Fluent软件模拟了OB-84型单级动叶可调轴流风机的流动特性，分析了单动叶安装角异常时的风机内流特征、熵产特性及噪声特性等。叶学民等[13-14]对异常叶片的偏离角度及周向分布情况进行了研究，分析了相邻和相间两动叶、相邻三动叶安装角异常下的风机内流特征和运行特性。对于两级动叶可调轴流风机的性能特征及动叶异常现象也逐渐引起了研究者们的重视，叶学民等[15]也对某600 MW机组配套的两级动叶可调轴流一次风机进行了全三维定常数值模拟，研究了前后级同相单叶片发生相同角度异常偏离时的风机性能变化。实际运行时，两级动叶可调轴流风机前后级动叶片也会发生异常偏离，前后级异常叶片相互影响进而产生干涉现象[16]，对于该异常现象的影响关系及影响机理还需要进行更深入的研究。笔者采用CFD数值模拟方法对两级动叶可调轴流风机进行全三维数值模拟，通过改变前后级单个异常动叶片的偏离角度，研究前后级单个异常动叶的干涉问题，分析前后级异常叶片分别发生不同角度异常偏离时风机相关性能参数及内流特征的变化规律，为两级动叶可调轴流风机的运行及设计提供参考依据。

1 物理模型及数值求解方法

1.1物理模型

以SAF36-25-2两级动叶可调式轴流引风机为研究对象，其结构见图1。

图1 SAF36-25-2 轴流引风机结构示意图

引风机从进口到出口依次为：集流器、第一级动叶、第一级导叶、第二级动叶、第二级导叶、扩压器。叶轮直径为3 600 mm，轮毂比为0.698，第一级、第二级动叶的动叶片数均为20，采用相同的扭曲机翼型叶片，第一、二级导叶的叶片数为23，第一级导叶采用长短相间布置的等厚圆弧板型叶片，第二级导叶采用相同均匀布置的等厚圆弧板型叶片。风机工作转速为745 r/min，旋转方向为逆时针(从进口方向看)，动叶安装角的调节范围为-35°～ +15°，对应开度从0%～100%调整。

1.2数值计算方法

根据风机的结构特点，建立轴流风机的全通道计算模型，将模型划分为集流区，前、后级动叶区，前、后级导叶区和扩压区六个计算区域，采用ICEM与TurboGrid软件结合的方式对各区域采用六面体结构性网格进行划分，对叶轮中流动梯度较大或曲率变化较大的区域进行局部网格加密(见图2)。

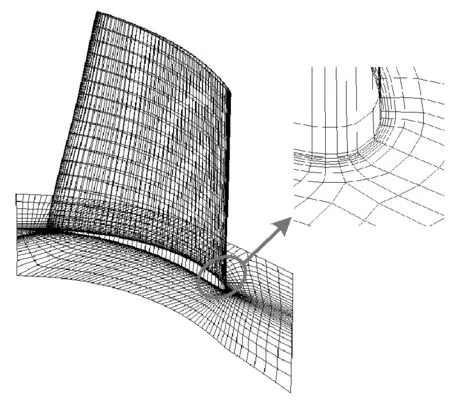
图2 叶片局部网格加密

模型将整个流道内流场视为不可压稳态黏性湍流流动，采用三维、定常、不可压缩的雷诺时均N-S方程组进行封闭，并采用SIMPLEC算法求解方程组。由于叶轮区存在旋转的动叶区和静止的导叶区，于是采用多参考坐标系模型对旋转区域和静止区域进行耦合，不同子域的交界面

上采用Interface进行信息的传递。将集流器进口作为风机进口，扩压器出口作为风机出口，分别采用速度进口、自由出流的边界条件，湍流模型采用旋转机械普遍适用的Realizablek-ε二方程模型，壁面采用标准壁面函数，近壁面采用无滑移边界条件。当计算残差达到10-4，且流场中监测点对应参数变化小于3%时，认定计算收敛。

笔者为研究前后级异常动叶的干涉现象，通过改变第一级异常叶片安装角度，分析第一级异常叶片对第二级叶轮性能及流场的影响。考虑到第二级异常叶片正反向偏离对风机性能影响的差异性，笔者将分别研究第二级异常动叶正反偏离两种情况下，第一级异常叶片对后级异常叶片的干涉问题，即Δβ2=±8°时，Δβ1=-12°～+12°对应的前后级异常叶片的干涉问题，具体变量选取见表1，其中Δβi表示第i级异常叶片的偏离角度。

表1 异常动叶片偏离角度值

图3为异常叶片偏离示意图，规定从叶顶向叶根看去，绕叶片旋转轴顺时针方向为反向偏离(Δβ<0)，逆时针方向为正向偏离(Δβ>0)。

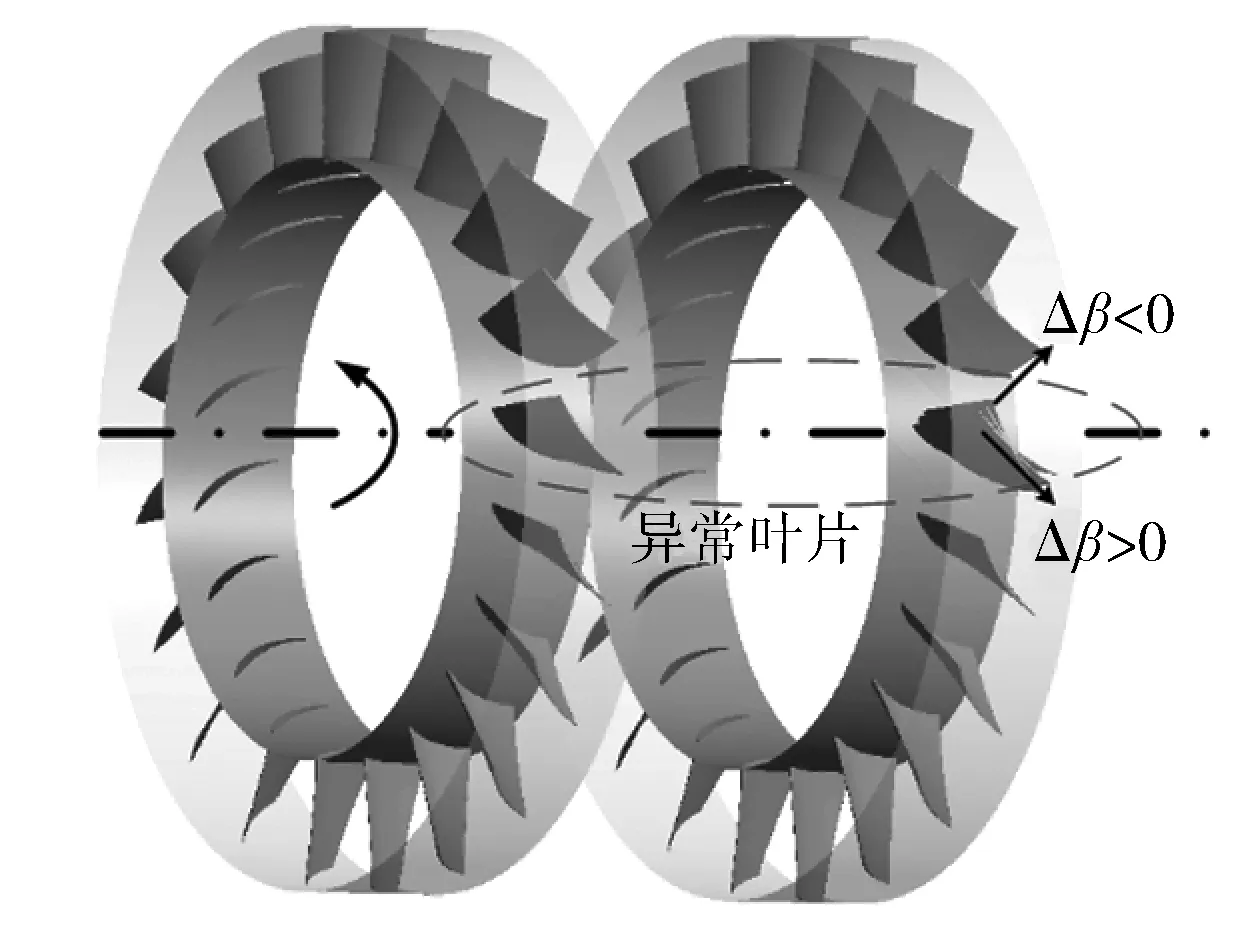
图3 异常叶片示意图

1.3网格无关性验证

为保证数值计算的可靠性，笔者对所选模型进行了网格无关性的验证，分别选取了5.3×106、5.7× 106、6.3×106、6.8×106网格数量进行计算，同时选取风机全压作为衡量值，随网格数增大的计算结果见图4。

由图4可以看出：在设计工况下(对应体积流量为505 m3/s，开度为0°)计算获得的风机全压随着网格数目的增加呈现先增大后趋向平缓的趋势，当网格数超过6.3×106时计算结果变化很小；网格数为6.3×106时模型计算出的全压和效率与实际值的平均相对误差分别为5.7%和6.9%，说明此时风机的数值计算精度满足计算要求且受计算网格数量的影响比较小。同时考虑时间成本，笔者采用总计算网格数为6.3×106的模型，其中动叶区和导叶区的网格数分别约为2.9×106和2.2×106，对于集流器和扩压器等区域设置网格较为稀疏，以减少计算量。

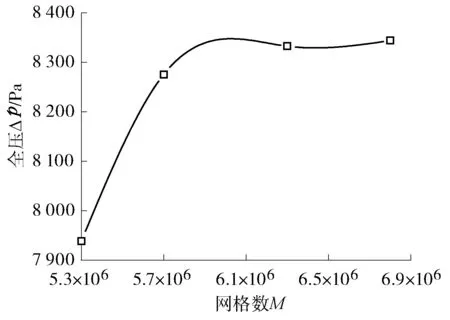
图4 计算网格数对引风机全压的影响

2 结果分析

2.1外特性曲线分析

图5和图6分别是第二级异常叶片偏离角度为+8°和-8°条件下，第一级异常叶片发生不同偏离角度时风机的外特性曲线。

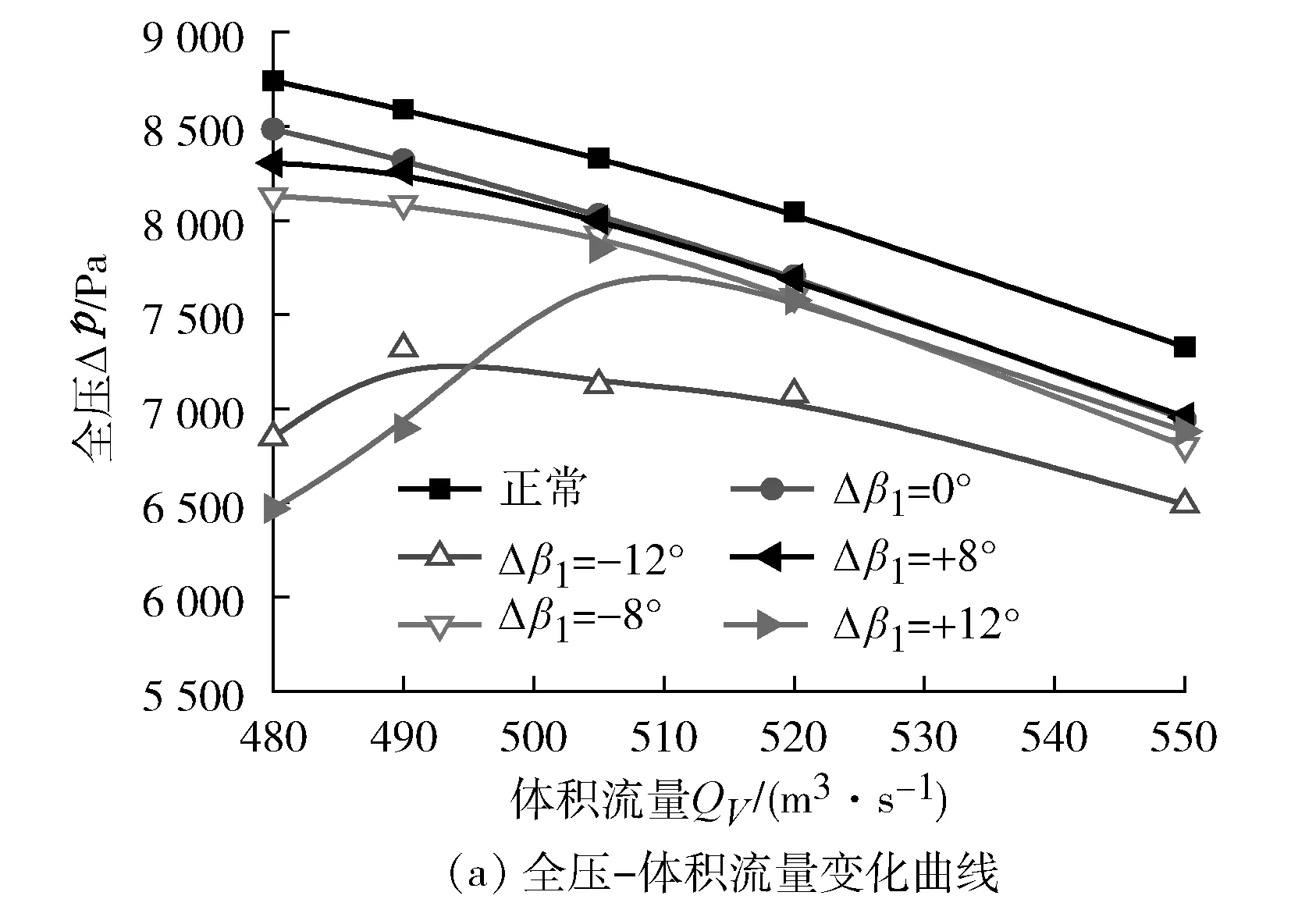
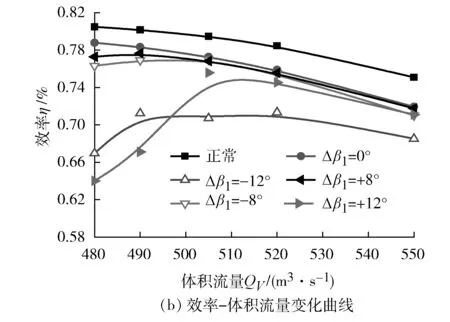
图5 Δβ2=-8°，不同Δβ1对应的风机外特性曲线

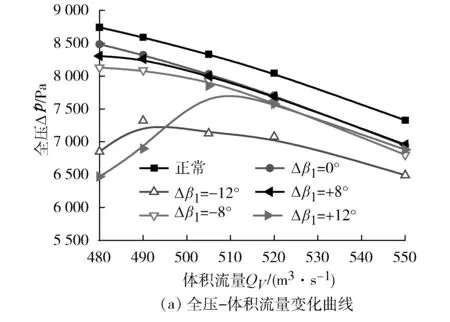
图6 Δβ2=+8°，不同Δβ1对应的风机外特性曲线

对比图5和图6可知：Δβ2正向偏离时，风机整体性能要优于反向偏离时风机的性能。Δβ1=±8°时，全压和效率随体积流量的变化趋势和正常情况基本一致，其中Δβ1=+8°对风机性能的影响最小，甚至在某些体积流量范围内的全压和效率要大于正常情况，这是因为叶片的异常偏离既会影响全压大小也会因为扰动流场造成流动损失，而单动叶安装角较小角度的正向偏离造成的流动损失要小于全压增加值。随着异常叶片偏离程度的增大，前后级异常叶片的干涉作用逐渐加强，造成风机全压和效率出现大幅度降低，在较小体积流量区域内干涉情况尤为明显，从而造成风机全压随体积流量的增加呈现先增大后减小的驼峰形曲线，使风机很容易进入失速状态。

图5表明：当Δβ2=-8°时，风机的全压和效率整体均低于正常情况，且随着异常叶片偏离程度的增大，风机性能出现明显的恶化，全压和效率出现大幅度的下降；当Δβ1=±12°时全压和效率随体积流量的增加呈现先增大后减小的驼峰形变化趋势。此外，Δβ1=+12°相较于Δβ1=-12°，失速点对应的体积流量更大，表明风机对应的不稳定工况区更大，风机更加容易发生失速故障；但是当Δβ1=-12°时，异常叶片在全体积流量范围内对风机性能的影响最大，如Δβ1分别等于-12°、-8°、0°、+8°、+12°时，对应的全压在全体积流量范围的平均降低比例分别为15.62%、6.40%、4.03%、4.67%、13.31%，效率分别平均降低12.14%、4.63%、3.12%、3.94%、11.05%。由此表明：Δβ2=-8°情况下，Δβ1=+8°时对整机整体性能影响较小，Δβ1=-12°时影响较大。

Δβ2=+8°时，异常叶片对风机性能的影响与Δβ2=-8°时风机性能的变化相似(见图6)，随着Δβ1从-12°增大到+12°，风机全压和效率的变化整体呈现先增大后减小的趋势，且在大体积流量工况下变化趋势和正常情况基本一致，但是Δβ2=+8°对应的风机性能要明显优于Δβ2=-8°时。此外，Δβ2=+8°时风机的外特性曲线变化还呈现如下特征：(1)Δβ1=+8°全压和效率基本和正常情况保持一致，甚至在部分体积流量范围内，全压高于正常情况；(2)相同偏离程度下，Δβ1<0°时风机性能明显比Δβ1>0时的风机性能差，以设计体积流量505 m3/s为例，在Δβ1-12°～+12°内，风机全压较正常情况下变化情况分别为-9.84%、-6.22%、+0.68%、-4.19%，效率的变化情况分别为-7.93%、-5.34%、-0.48%、-4.84%。

2.2第二级叶轮特性曲线分析

为探讨两级叶片同时出现异常偏离时第一级异常叶片对第二级叶轮性能的干涉影响，对下列各情况下第二级叶轮的全压及效率随体积流量的变化情况进行分析(见图7)。

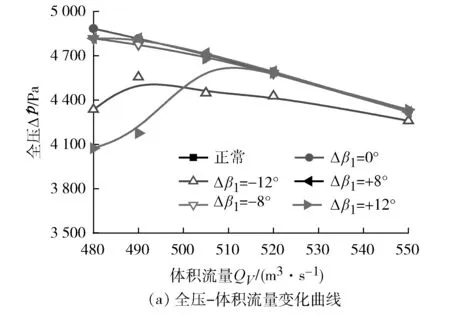
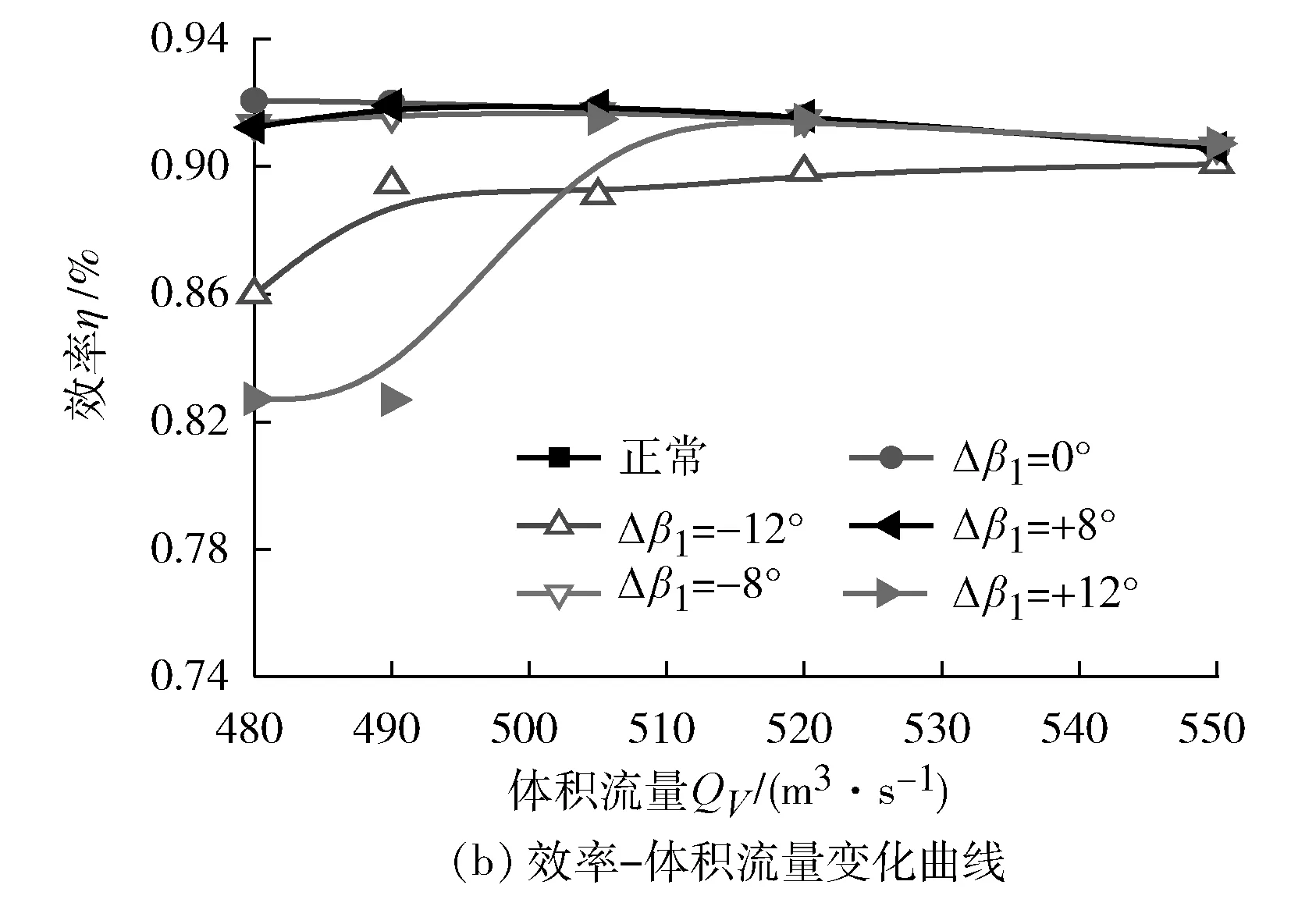
图7 Δβ2=-8°，不同Δβ1对应的第二级叶轮特性曲线

当第二级叶轮异常叶片偏离角度保持不变时(Δβ2=-8°)，第二级叶轮的全压及效率的特性曲线受到第一级叶轮异常叶片偏离角度的影响出现一定程度的变化。

当Δβ1=±8°时，第二级叶轮的全压及效率变化趋势和正常情况基本相同，第一级叶轮的异常叶片对第二级叶轮性能的影响比较小；当Δβ1=±12°时，第二级叶轮的全压及效率随体积流量的增加呈现先增大后减小的驼峰形变化趋势，且Δβ1=+12°与-12°对应的第二级动叶轮的特性曲线存在交点，当体积流量小于交点所对应的体积流量时，Δβ1=-12°时第二级叶轮全压及效率要大于Δβ1=+12°时，当体积流量大于交点对应的体积流量时，情况与之相反。此外Δβ1=-12°，各体积流量范围内全压和效率都出现了一定程度的降低，而Δβ1=+12°时，第二级叶轮的全压仅在小于一定流量时出现明显的降低，且降低幅度较大。

图8为第二级异常叶片偏离角度为+8°时，第一级叶轮异常叶片偏离不同角度时对第二级叶轮做功能力的影响。

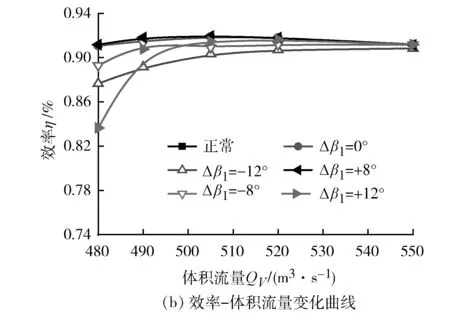
图8 Δβ2=+8°，不同Δβ1对应的第二级叶轮外特性曲线

当Δβ1=+8°时第二级叶轮的测试体积流量范围内全压及效率和Δβ1=0°时基本一致，甚至在某些体积流量范围内高于第一级叶片正常的情况。与图7有所不同的是当Δβ1=-8°时，叶轮全压和效率出现较为明显的降低，且随着异常叶片偏离程度的增大，叶轮性能逐渐恶化，当Δβ1=+12°时，全压呈现明显的驼峰形曲线。

对比分析图7和图8可知：Δβ2=-8°情况下，第一级叶轮同相异常叶片发生较小角度异常偏离时(Δβ1=±8°)，第一级异常叶片对第二级叶轮的干涉影响很小，几乎可以忽略不计，而较大角度异常偏离时(Δβ1=±12°)，第二级叶轮的性能受到第一级异常叶片的干涉影响出现较大幅度变化；而当Δβ2=+8°时，第一级异常叶片偏离角度对第二级叶轮性能影响相对比较明显，除Δβ1=+8°以外，其他异常偏离角度都会使第二级叶轮的做功能力降低，全压和效率出现明显的降低。随着第一级异常动叶偏离程度的增大，第二级动叶轮全压和效率都出现明显的驼峰形曲线，且Δβ=+12°对应的不稳定工况区要比Δβ=-12°时更大，运行过程中第二级叶轮更容易进入失速状态，说明此时第一级异常叶片对第二级叶轮性能的干涉影响更大。

2.3导叶效率

动叶安装角异常不仅会对叶轮自身的做功能力产生影响，其引起的流场变化对导叶的扩压能力也会产生重要影响。第二级叶轮叶片安装角发生一定角度异常情况下，第一级同相叶片发生不同角度异常偏离时对第一级导叶性能的影响见图9(实线和虚线分别表示第二级异常叶片反向偏离-8°及正向偏离+8°时第一级导叶的效率变化情况)。

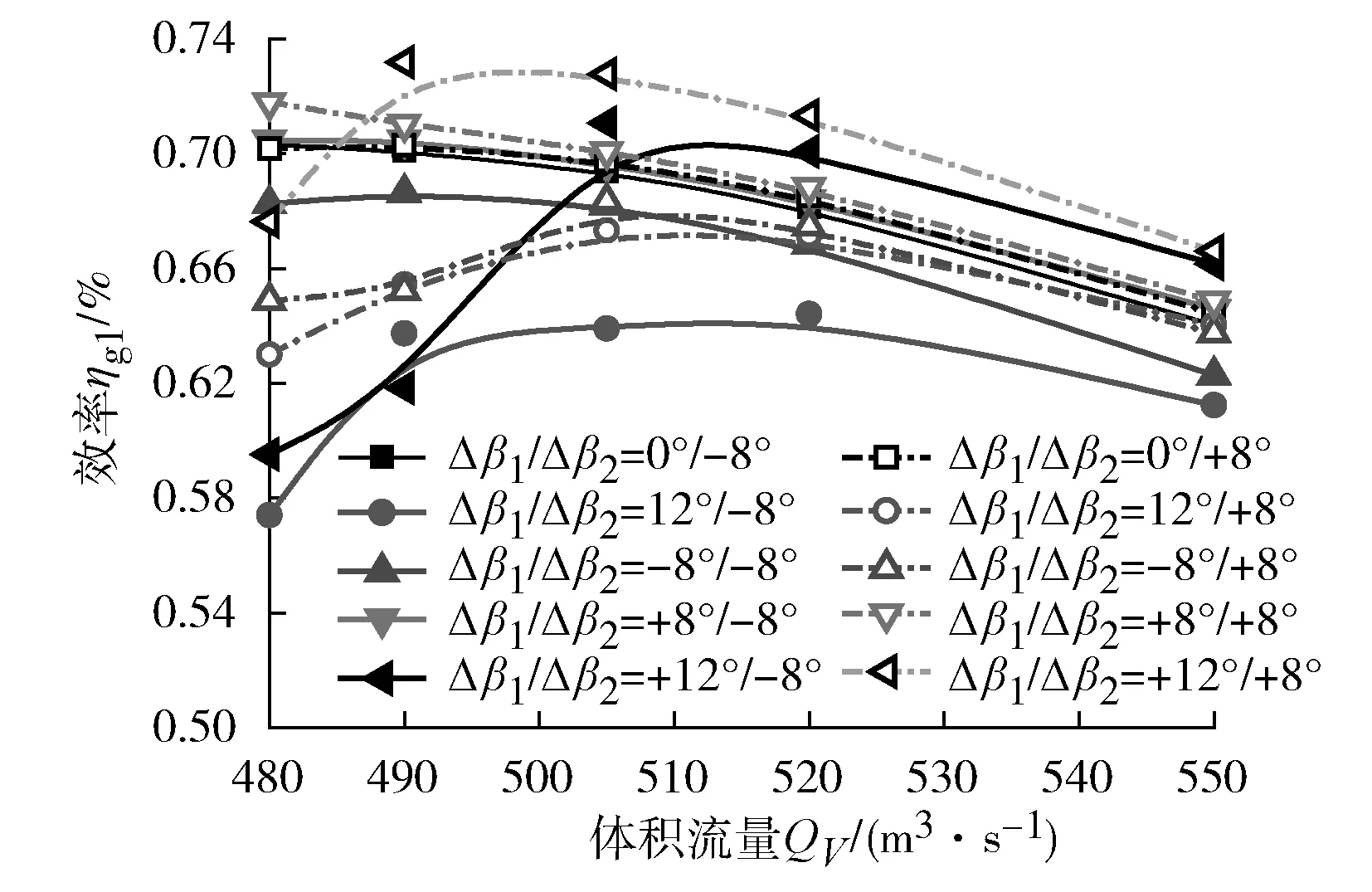
图9 Δβ2=±8°，不同Δβ1对应的第一级导叶效率变化曲线

从图9可以看出：当两级动叶同时发生安装角异常偏离时，第二级异常叶片正反偏离对第一级导叶的导叶效率有着不同的影响。Δβ2=+8°时第一级导叶的导叶效率要整体大于Δβ2=-8°时，说明第二级叶轮异常叶片对前一级导叶的性能也有一定的干涉影响。Δβ2不变情况下，当Δβ1=+8°时，导叶效率受第一级异常叶片的影响比较小，这与第二级叶轮性能的变化情况相类似，说明第一级异常叶片正向偏离+8°时，第一级异常叶片对后面各级导叶及动叶的干涉影响都比较小。当Δβ1=±12°时，第一级异常叶片对后续导叶的扩压性能产生较大影响，导叶效率随体积流量的变化呈现先增大后减小的趋势，但是与风机整体性能变化又有些不同的是，当Δβ1=+12°时，在大部分体积流量范围内，导叶效率较正常情况有很大提高，尤其是当Δβ2=+8°时导叶效率在全体积流量范围内都比较高，而Δβ1=-12°时第一级导叶的扩压能力出现严重的恶化，导叶效率出现大幅度的降低。

2.4风机内部流场分析

叶轮内部流场是反映风机性能的最直观因素，为进一步探讨前后级异常叶片的干涉情况，图10～图12分别给出了设计工况叶片正常、第二级单动叶异常及两级叶轮同相单叶片同时异常偏离情况下0.5叶高截面处流线图(图中旋转部分速度为相对速度，静止部分速度为绝对速度)。

图10 叶轮正常及第二级单叶片正反小角度异常偏离时0.50叶高处叶轮截面流线图

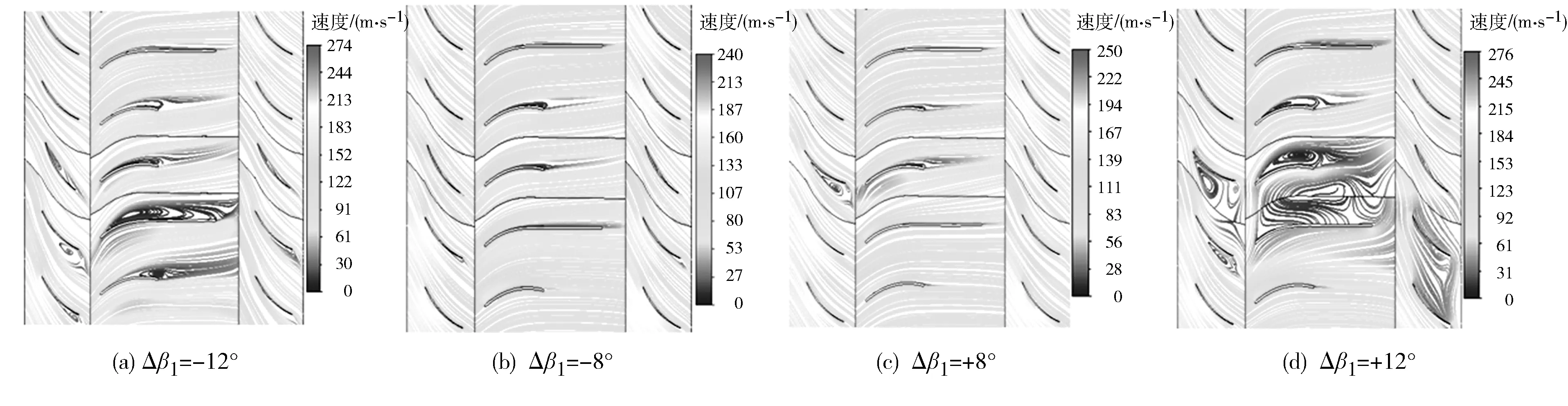
图11 Δβ2=-8°时0.50叶高处叶轮截面流线图

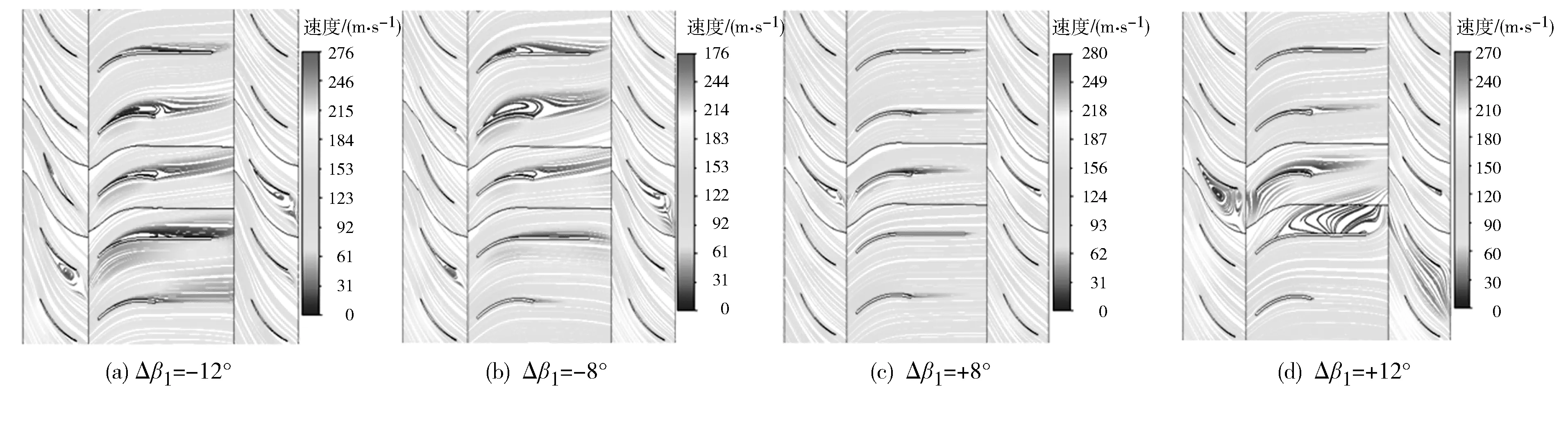
图12 Δβ2=+8°时0.50叶高处叶轮截面流线图

从图10可以看出：风机正常运行时，叶轮内部流场分布相对比较均匀，当第二级发生单叶片正反较小角度异常偏离时(Δβ2=±8°)，异常叶片对前级导叶的影响相对比较小，仅在导叶尾缘出现较小尾涡。对比图11和图12可知：当前后两级同相叶片都发生一定角度异常偏离时，第二级异常叶片的偏离方向对叶轮内部流场的影响则有所不同。Δβ2=+8°时叶轮流道内因异常叶片造成的漩涡区要比Δβ2=-8°时小，说明第二级异常叶片发生正向偏离时风机性能要优于反向偏离时风机性能。由图11(c)与图12(c)可以看出：当第一级异常叶片发生较小角度异常偏离时，叶片尾缘形成尾涡，随着流体的流动带入到导叶中，经导叶对尾涡的整流，尾涡消失，流线在周向上变得均匀，进入到第二级叶轮的流体受第一级异常叶片的影响较小，即第一级异常叶片对第二级叶轮的干涉影响相对较小。而当第一级叶片发生较大角度异常偏离时，异常叶片使第一级导叶流道内产生较大漩涡，阻塞流体流动，导叶虽在一定程度上减小了前后级异常叶片的干涉，但是第二级叶轮流道内流场的均匀性依然受到第一级异常叶片的影响而被破坏。此外Δβ1=+12°异常叶片对流场的影响要比Δβ1=-12°时的影响大。

综合对比图10、图11、图12可以看出：第二级叶轮叶片异常偏离时不仅对本级叶轮内流场产生影响，对上级叶轮内流场也会产生一定干涉影响，第二级叶轮异常叶片发生较小角度的正向偏离时异常叶片对流场的干涉影响要小于反向偏离时。当第一级叶轮叶片发生异常偏离时，异常叶片会破坏第二级叶轮流道内流场的均匀性，使流道内产生漩涡阻塞流道，从而破坏进入第二级叶轮流场的均匀性，使第二级叶轮流道内也很容易发生漩涡阻塞流道造成风机性能大幅下降。另外，前后级异常叶片之间的导叶在一定程度上减小了异常叶片的干涉，但随着异常叶片偏离程度的增大，第二级叶轮受第一级异常叶片的干涉影响则逐渐增大。

3 结语

笔者采用数值模拟的方法在前后级动叶轮单叶片发生不同角度异常偏离时，研究异常叶片对风机性能参数的影响规律及前后级异常叶片的干涉关系。主要结论有：

(1) 第二级异常叶片偏离角度β2=+8°时风机整体的性能要优于β2=-8°时，且β2保持不变情况下，β1从-12°增加到+12°的过程中，全压和效率呈现整体先增大后减小的变化趋势，异常叶片对风机性能的影响在小体积流量区域尤为突出。此外，β1=+8°时对风机整体性能的影响最小，而β1=-12°时影响最大。

(2) 第二级叶轮的做功能力在受到本级异常叶片偏离角度影响的同时，也会受到第一级异常叶片偏离角度的干涉影响。第一级异常叶片对第二级叶轮性能的影响与对风机整体性能影响的变化规律基本一致，即随着第一级异常叶片偏离程度的增大，全压和效率出现明显降低，异常叶片造成的失速点对应流量增大，对应失速区范围增大，第二级叶轮更容易进入失速区。

(3) 两级动叶之间的导叶在一定程度上减小了前后级异常叶片的干涉，第一级叶片发生较小角度异常偏离时，第一级异常叶片对第二级叶轮的干涉影响相对比较小，而第一级异常叶片发生较大角度异常偏离时的干涉影响则相对比较大。

[1] 李海送. 动叶可调轴流通风机动叶漂移原因分析及预防措施[J]. 中国科技信息, 2012(9): 117-118.

[2] 陈建飞. 600 MW机组一次风机故障分析及处理[J]. 华电技术, 2015, 37(6): 48-51, 53.

[3] 李俊, 叶学民, 王松岭. 电站轴流风机常见故障及处理措施[J]. 发电设备, 2008, 22(3): 231-236.

[4] 童红政, 吴伟. 电站轴流风机喘振的危害及预防措施[J]. 发电设备, 2007, 21(4): 292-293.

[5] 张磊, 郎进花, 王松岭. 电站轴流风机旋转失速工况下的叶轮静力特性研究[J]. 动力工程学报, 2015, 35(5): 387-393, 417.

[6] FUKANO T, JANG C M. Tip clearance noise of axial flow fans operating at design and off-design condition[J]. Journal of Sound and Vibration, 2004, 275(3-5): 1027-1050.

[7] KERGOURLAY G, KOUIDRI S, RANKIN G W, et al. Experimental investigation of the 3D unsteady flow field downstream of axial fans[J]. Flow Measurement and Instrumentation, 2006, 17(5): 303-314.

[8] 叶学民, 李新颖, 李春曦. 第一级导叶改进对两级动叶可调轴流风机性能的影响[J]. 动力工程学报, 2014, 34(3): 228-235, 252.

[9] CATTANEI A, GHIO R, BONGIOVI A. Reduction of the tonal noise annoyance of axial flow fans by means of optimal blade spacing[J]. Applied Acoustics, 2007, 68(11-12): 1323-1345.

[10] CAROLUS T, SCHNEIDER M, REESE H. Axial flow fan broad-band noise and prediction[J]. Journal of Sound and Vibration, 2007, 300(1-2): 50-70.

[11] 黄超. 大型动叶可调轴流风机数值模拟与实际工况比较研究[D]. 北京: 华北电力大学, 2011.

[12] 李春曦, 尹攀, 叶学民. 单动叶安装角深度异常对轴流风机性能及噪声影响的数值模拟[J]. 中国电机工程学, 2012, 32(35): 122-129.

[13] YE X M, LI C X, WANG S L, et al. Internal flow characteristics of a variable pitch axial fan under abnormal installation angles of a single blade[J]. Advanced Science Letters, 2011, 4(6-7): 2164-2169.

[14] 叶学民, 李俊, 李春曦, 等. 轴流风机多动叶安装角非同步调节下的内流特征和运行特性[J]. 中国电机工程学报, 2010, 30(32): 77-83.

[15] 叶学民, 李新颖, 李春曦. 两级动叶可调轴流风机内流特征的数值模拟[J]. 动力工程学报, 2013, 33(11): 871-877.

[16] 肖朋, 王军. 对旋叶栅级间内流干涉的数值研究[J]. 热能动力工程, 2006, 21(3): 249-254, 323.

StudyonInterferenceEffectsbetweenFirst-andSecond-StageAbnormalBladesofanAxialFlowFan

Feng Yao1, Dong Yunshan1, Si Fengqi1, Bai Delong2, Xie Guanyu2

(1. Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, Southeast University, Nanjing 210096, China; 2. Inner Mongolia Daihai Power Generation Co., Ltd.,Ulanqab 012000, Inner Mongolia Autonomous Region, China)

To solve the problem of abnormal drifts of installation angles existing in the first- and second-stage blades of a SAF36-25-2 two-stage adjustable axial-flow induced-draft fan, Fluent software was applied to research the change rules of fan performance parameters and the interference relation of abnormal blades in the first- and second-stage. Results show that the overall fan performance at an abnormal drift angle of Δβ2=+8° in the second impeller is better than that at Δβ2=-8°. Keeping the Δβ2unchanged, when the abnormal drift angle in the first impeller changes from -12° to +12°, the fan performance increases first and then decreases, and both the fan pressure and efficiency show the most evident deterioration in the whole flow range at Δβ1=-12°, whereas the abnormal blade has the least effect on the fan performance at Δβ1=+8°. With the increment of drift angle, the interference effects of the first-stage abnormal blade on the performance of the second-stage impeller would be enhanced.

axial-flow induced-draft fan; rotor blade; installation angle; performance characteristics

2017-02-28；

2017-05-20

江苏省产学研前瞻性联合研究项目(BY2015070-17)

封 遥(1992—)，男，在读硕士研究生，主要从事叶轮机械及空气动力学方面研究。E-mail: fy_ryan@163.com

TH443

A

1671-086X(2017)06-0383-07