有限域F24上的四阶MDS矩阵的计数

陈国源

（广州大学 数学与信息科学学院，广东 广州 510006）

有限域F24上的四阶MDS矩阵的计数

陈国源

（广州大学 数学与信息科学学院，广东 广州 510006）

本文主要研究了有限域F24上的四阶MDS矩阵的计数. 在有无限制生成的四阶矩阵互不相同的情况下，回归分析了矩阵个数与MDS矩阵平均个数的线性关系，发现两种情况下，二者均呈良好的线性关系，但不作限制可以节省搜索时间，使算法的扩散性能最佳.

有限域；MDS矩阵；计数

随着互联网的普及，信息安全问题也越来越受关注，现代密码技术是解决互联网信息安全的重要技术之一. Shannon在《保密系统的通信理论》[1]中提出：设计现代密码算法需要包含混淆层和扩散层这两个重要的部件. 其中，通常使用几个并置的非线性S盒来构造混淆层. 对于扩散层，则一般利用线性映射实现. 安全性能良好的扩散层可有效抵抗密码分析（如线性分析[2]和差分分析[3]等）.而MDS矩阵[4-6]的分支数最大，扩散性能最佳，可以最大限度地保证在线性和差分分析下的安全性，也因此常被用作对称密码中的线性扩散层，如Rijndael[7]和Square[8]等. 有限域是一种特殊的域，只含有有限个元素，但在密码学领域有着广泛应用. 其中MDS矩阵的生成与检验就可以在有限域中进行. 在有限域中进行运算前，要先对有限域中的元素进行表示. 矩阵的生成就是利用表示后的有限域中的元素构成的矩阵；而矩阵的检验过程就相当于在有限域中的运算. 通过对生成的矩阵进行检验，满足条件的矩阵就是MDS矩阵. 令MDS矩阵作为对称密码中扩散层的线性映射，算法的扩散性能达到最佳.

本文通过有限域[9-10]构造了四阶MDS矩阵，给出其运算法则；进而研究四阶MDS矩阵的计数问题[11-12]，并进行相应的实验统计分析[13].

1 有限域中元素的表示

根据有限域的定义，有限域F2n中只含有2n个元素. 下面使用多项式表示有限域F24中的元素，F24是F2的4次扩张，f(x)=1+x+x4∈F2[x]是不可约的，若α是F2上的15次本原单位根，则其有限域的元素表示如表1所示，而F24中元素的加法为普通的多项式加法，乘法为模f(x)的多项式乘法.

表1 有限域的元素表示

2 四阶MDS矩阵的个数

定理1[14]若矩阵A是一个MDS矩阵，当且仅当矩阵A的所有子方阵都是可逆的，即矩阵A的所有子方阵的行列式均不等于零.

由于样本空间比较大，故没有穷搜有限域F24上的所有四阶矩阵，而是采用随机生成四阶矩阵的方法，再对随机生成的矩阵进行检验，若满足定理1的矩阵就是所求矩阵，即MDS矩阵. 因元素取自有限域F24上的四阶矩阵规模比较大，而且由于随机生成的矩阵的随机性，若只进行一次测试，实验结果误差会比较大，所以这里进行了多次试验（这里取试验次数为T=5），再求平均MDS矩阵的个数的方法，以保证数据结果的稳定性.

2.1 随机生成互不相同的矩阵

本实验对生成的矩阵做了一个小限制——生成的四阶矩阵互不相同，实验数据如表2所示.

表2 MDS矩阵的实验个数统计

观察表2可以发现，当生成1 000个矩阵时，其中约有5个为MDS矩阵；当生成10 000个矩阵时，其中约有42个矩阵是MDS矩阵；当生成100 000个矩阵时，其中约有453个矩阵是MDS矩阵. 通过表2还可以知道：当随机生成的矩阵个数递增时，对应的MDS个数也呈现递增的趋势. 因此对随机生成的矩阵个数和相应得到的平均MDS矩阵个数在进行散点分析. 选取随机生成的矩阵个数为自变量x，MDS矩阵的平均个数为y.利用Matlab软件作散点图，如图1所示.

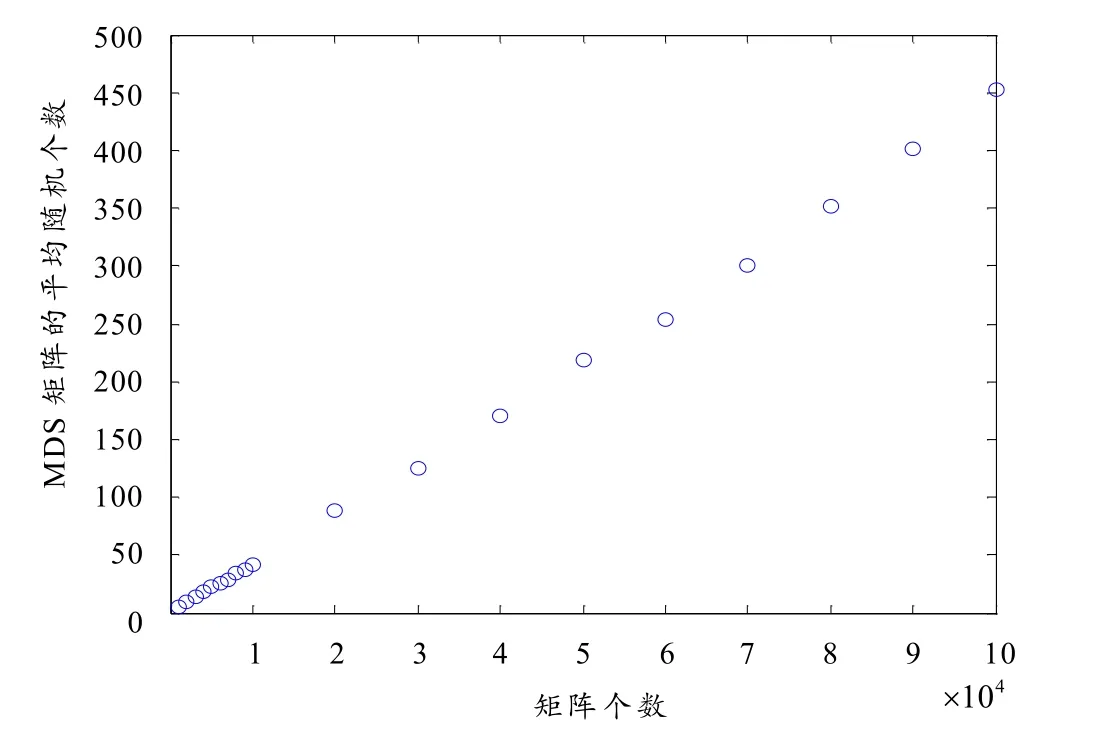
图1 散点图（要求生成互不相同的矩阵）

由散点图可以发现，数据点成条状分布，随机生成的矩阵个数和相应得到的平均MDS矩阵个数有较好的线性相关关系，因此可以用回归直线来近似刻画它们之间的关系. 而通过Matlab软件进行拟合可以得到如下回归直线：

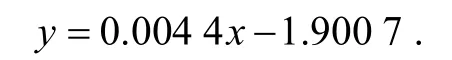
通过计算，R2=0.999 0.R2反映了回归模型拟合数据的效果，R2越接近1，残差平方和越小，表示回归的效果越好. 即该回归直线能很好地描述随机生成的矩阵个数和相应得到的平均MDS矩阵个数之间的关系，故可以用得到的直线进行预测估计元素取自有限域F24上的四阶MDS矩阵的个数.

2.2 随机生成可重复的矩阵

当随机生成互不相同的矩阵的个数较大时，不管是生成过程，还是检验过程，需要付出的时间代价都是非常大的. 为了减少这种代价，需要对检验随机生成互不相同的矩阵作进一步的调整，以寻求在不牺牲时间为代价的前提下而获得较为可靠的结果. 下面将不再要求生成的矩阵互不相同（即随机生成的矩阵是可重复的）的情况进行讨论分析. 通过随机搜索得到的相关数据如表3所示.

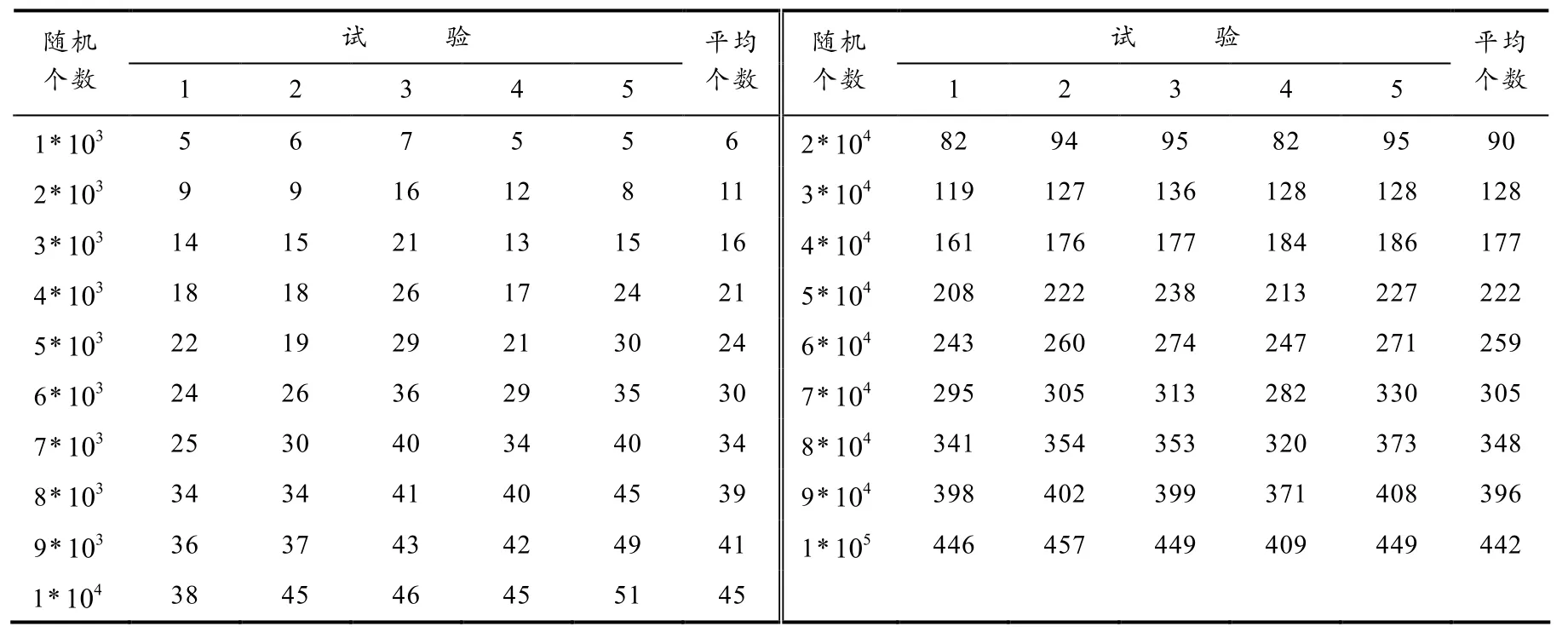
表3 MDS矩阵的实验个数统计

对随机生成的矩阵个数和相应得到的平均MDS矩阵个数在进行散点分析. 选取随机生成的矩阵个数为自变量x，MDS矩阵的平均个数为y. 利用Matlab软件作散点图，如图2所示.

由散点图可以发现，数据点成条状分布，随机生成可重复的矩阵个数和相应得到的平均MDS矩阵个数也有较好的线性相关关系，因此也可以用回归直线来近似刻画它们之间的关系. 同理可得，随机生成可重复的矩阵个数和相应得到的平均MDS矩阵个数的回归直线为：

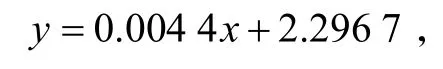
同时也可以得到相应的相关指数R2=0.9998. 这表明了该回归直线能很好地描述随机生成可重复的矩阵个数和相应得到的平均MDS矩阵个数之间的关系.

图2 散点图（随机生成的矩阵可重复）

2.3 结果与讨论

由2.1和2.2的分析可以对上述情况进行数据的拟合，拟合结果如图3.

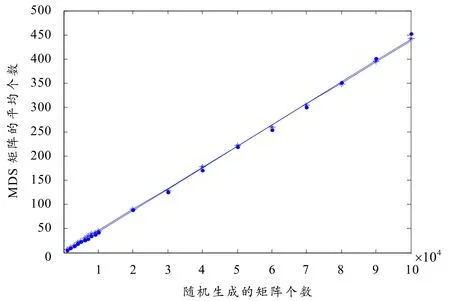
图3 拟合

通过上文和图3分析可得，随机生成的矩阵互不相同或矩阵可重复出现得到的拟合直线的回归系数相等，而回归截距相差并不大. 随着实验数据的不断增加时，两条回归直线近似相等，故对MDS矩阵的统计个数的影响不大. 同时可以得到以下结论：

结论1设矩阵A是有限域F24上随机生成的一个四阶矩阵，则矩阵A为MDS矩阵的概率为

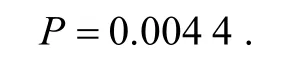
结论2在有限域F24上，四阶的MDS矩阵个数约为0.044*264个.

例1若随机生成106个四阶矩阵，则其中大约会有4 400个为MDS矩阵.通过试验检测的数据如表4所示.

表4 随机生成106个矩阵中的MDS矩阵的个数

由表4，随机生成106个四阶矩阵，可得到4 307个矩阵是MDS矩阵，与理论4 400个相差并不是很大，因此，可利用本文得到的理论概率去估计有限域F24上的四阶MDS矩阵的个数.

3 结束语

本文研究了元素取自有限域F24的MDS矩阵的生成与检验，通过使用Matlab软件进行试验检验，统计满足条件的四阶MDS矩阵的个数，进而解决有限域F24上的四阶MDS矩阵的计数问题. 本文是一个初步的探究，下一步研究可对统计概率的理论证明和算法的改进等，从而提高结果的稳定性和提升运行效率.

[1] SHANNON C E. Communication theory of secrecy systems [J]. Bell System Technical Journal, 2015, 28(4)∶656-715.

[2] BIHAM E, SHAMIR A. Differential cryptanalysis of DES-like cryptosystems [J]. Journal of Cryptology, 1991,4(1)∶ 3-72.

[3] MATSUI M. Linear cryptanalysis method for DES cipher [C]//Advances in Cryptology—EUROCRYPT’93.Berlin Heidelberg∶ Springer, 1993∶ 386-397.

[4] RIJMEN V, DAEMEN J. The cipher SHARK [C]//Proceedings of the Third International Workshop on Fast Software Encryption. London∶ Springer-Ver log, 1996∶ 99-112.

[5] 刘丽辉，裴焘，张祖平. MDS矩阵的生成与应用[J]. 现代通信技术，2014(1)∶ 26-29.

[6] 李鹏飞，李永强. MDS矩阵的构造方法[J]. 网络与信息安全学报，2016, 2(6)∶ 44-53.

[7] DAEMEN J, RIJMEN V. The design of Rijndael∶ AES，the advanced encryption standard [M]. Berlin Heidelberg∶ Springer, 2002.

[8] DAEMEN J, KNUDSEN L R, RIJMEN V. The block cipher square [C]//Pooceedings of the 4th International Workshop on Fast Software Encryption. London∶ Springer-Verlag, 1997∶149-165.

[9] 裴定一，徐祥. 信息安全数学基础[M]. 北京：人民邮电出版社，2007.

[10] 林东岱. 代数学基础与有限域[M]. 北京∶高等教育出版社，2006.

[11] 周旋，张欣，瞿成勤. MDS矩阵的比特变换性质及计数研究[J]. 计算机工程与科学，2010, 32(4)∶ 33-35.

[12] 吴文玲，冯登国，张文涛. 分组密码的设计与分析[M]. 2版. 北京：清华大学出版社，2009.

[13] 刘东华，向良军. 信道编码与MATLAB仿真[M]. 北京：电子工业出版社，2014.

[14] MACWILLIANS F J, SLOANE N J A. The theory of error correction codes [M]. New York∶ North-Holland Publishing Company, 1977.

[责任编辑：韦 韬]

Enumeration of Fourth Order MDS Matrices over the Finite Fields ofF24

CHEN Guo-yuan
(School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China)

The paper mainly researches the enumeration of fourth order MDS matrices overF24. For the different four-order matrices generated under restricted conditions, a regression analysis of the linear relationship between the number of matrices and average number of MDS matrices reveals that the two are in a benign linear relationship, but dispensing with restrictions can save the search time and optimize the diffusion performance of the algorithm.

finite fields; MDS matrices; counting

O156.2；TN918.1

A

1006-7302（2017）04-0011-05

2017-07-10

陈国源（1992—），男，广东珠海人，在读硕士生，主要研究方向为应用数学（密码学）