振动筛系统双Hopf分岔的反控制

张思进+杜伟霞+殷珊

摘 要：振动筛系统是一类非光滑度很高的多参数非线性动力系统，传统的分岔准则无法直接适用，这里采用了新的不依赖于特征值计算的显式分岔临界准则，以实现振动筛系统双Hopf分岔的反控制.首先，根据系统的运动方程得到Poincaré映射在不动点处的线性化矩阵；然后，对系统施加线性反馈控制器，得到受控后的Poincaré映射，根据分岔临界准则求得双Hopf分岔的显式临界条件；最后，通过模态叠加法对两类系统分别进行了数值模拟.结果显示，在相同的系统参数下线性反馈控制器通过调整控制参数，可以有效地实现双Hopf分岔的反控制.双Hopf分岔可以提高一些振动机械的工作效率，具有一定的实际意义.

关键词：双Hopf分岔反控制；非光滑；显式分岔临界准则；线性反馈控制器

中图分类号：O322； TH113 文献标志码：A

Anti-control of Double Hopf Bifurcation of VibrationRating Griddle System

ZHANG Sijin，DU Weixia， YIN Shan

（College of Mechanical and Vehicle Engineering，Hunan University，Changsha 410082，China）

Abstract：The vibrating griddle system is a kind of nonlinear multi-parameter dynamical system with high non-smoothness，and traditional bifurcation criterion cant be applied directly. Therefore，a new explicit bifurcation criterion independent on eigenvalue calculation was adopted to achieve the anti-control of double Hopf bifurcation for vibrating griddle system. Firstly，the Poincaré mapping at the fixed point was obtained according to the motion equation of the system. Then，a linear feedback controller was applied to the system to obtain the controlled Poincaré mapping，and the explicit critical condition of double Hopf bifurcation was obtained according to the bifurcation critical criterion. Finally，numerical simulation of the two types of systems was carried out by the modal superposition method. The results show that the linear feedback controller can effectively achieve the anti-control of double Hopf bifurcation by adjusting the control parameters under the same system parameters. Double Hopf bifurcation can improve the working efficiency of some vibration machinery，so it has certain practical significance.

Key words：double Hopf bifurcation anti-control；non-smooth；explicit critical criterion of bifurcation；linear feedback controller

近几十年来，由于振动筛结构简单、处理能力强、工作可靠，得到了很快的发展，并广泛应用在煤炭、采矿、建筑、冶金等多种行业.对于振动筛的研究基本上是以生产实际为导向，力求提高筛分效率，提高产品质量，降低能源消耗.文献[1-2]采用数值分析与试验相结合的方法对其动态特性和内部应力进行了分析，结果表明振动筛固有频率和工作频率保持在合理范围内可避免共振.文献[3-4]运用多轴疲劳分析的临界平面法对大型直线振动筛进行了疲劳寿命数值分析，运用应力-强度干涉模型对其可靠性进行了预测.文献[5]记录了振动筛的研究进展情况，提出了尽管研究已经进展得很好，但是还有很多未解決的问题，像物料与筛面碰撞中的分岔、混沌等非线性现象.

由于振动筛的强非线性和非光滑性，使得振动筛的动力学行为相当复杂，因此振动筛的分岔和混沌行为成了近年来非线性动力学领域的热门研究课题.白亮亮等[6]对振动筛系统的非线性响应进行了分析，在进行仿真后，发现了其存在Flip分岔、Neimark-Sacker分岔、环面倍化分岔以及Hopf-Hopf分岔，并向混沌演化，提出了当振动筛与物料有相同的振动频率时，物料的分离效果最佳.张永祥等[7]基于Poincaré 映射研究了系统的余维三分岔和非常规的混沌演化过程，在分岔点附近发现了三角形吸引子、“五角星型”、“轮胎型”概周期吸引子.虽然近年来不少

研究者开始研究分岔的反控制[8-13]，但是有关振动筛的分岔反控制研究还是很少，文献[14-15]研究了二自由度振动落砂机周期倍化分岔的反控制.endprint

本文通过振动筛的力学模型，对物料与筛面碰撞中的分岔进行了探究，并把文献[11]提出的反控制理论应用在振动筛上，通过数值计算，得出原系统在线性反馈控制器的作用下通过调节控制参数得到双Hopf分岔解，实现了双Hopf分岔的反控制.对于一些振动系统像落砂机、筛分机、振动棒、搅拌机等，双Hopf分岔产生的环面概周期运动可以提高该类系统的工作效率，比如可以使搅拌机搅拌得更均匀，使筛分机筛分得更快，因此，实现双Hopf分岔的反控制具有一定的实际意义.

1 运动方程以及Poincaré映射

振动筛系统的力学简化模型如图1所示，质量为M1和M2的振子分别由刚度为K1和K2的两个线性弹簧以及阻尼系数为C1和C2的线性阻尼器相连接，振子只在垂直方向上运动，对M1施加简谐激振力Psin（Ωt+τ）.质量块M3在重力作用下从上方落下并与M1产生碰撞，改变速度后以新的初值运动，如此往复.设该模型里的阻尼是Rayleigh型比例阻尼，碰撞恢复系数为R.

振动筛系统的运动微分方程是：

M11+（C1+C2）1-C22+（K1+K2）q1-K2q2=Psin（ΩT+τ），

M22-C21+C22-K2q1+K2q2=0，3=-g.（1）

式中：q1，q2，q3分别是振子M1，M2，M3的位移；M1和M3之间的间隙是e.

将以上微分运动方程无量纲化为：

100m12+2ζ1+c-c-kk12

+1+k-k-kkx1x2=10sin（ωt+τ），3=-l（2）

其中无量纲量为：

m=M2/M1，k=K2/K1，c=C2/C1，

ζ=C1/（2M1ωn1），ωn1=K1/M1，

xi=qiK1/P，ω=ΩM1K1，t=TK1M1，

l=M1gP，δ=eK1/P，γ=M3/M1，

（i=1，2，3）

当q1-q3=e时，即x1-x3=δ，系统将发生碰撞.由碰撞前后系统动量守恒和恢复系数的定义，振子M1与M3碰撞前后的速度关系为：

1-+γ3-=1++γ3+，

1+-3+=-R（1--3-），（3）

式中：1-，1+和3-，3+分别表示振子M1，M3碰撞前后的瞬时速度；R表示碰撞恢复系数.

设振子碰撞前的瞬时为0时刻，则下一次振子碰撞前的瞬时为2nπ/ω，n∈Z.系统周期运动的初始条件是：

x1（0）=x3（0）=x1（2nπ/ω）

=x3（2nπ/ω）=x10，

x2（0）=x2（2nπ/ω）=x20，

2（0）=2（2nπ/ω）=20，

1（0）=1-γR1+γ1（2nπ/ω）+

γ（1+R）1+γ3（2nπ/ω）=10，

3（0）=1+R1+γ1（2nπ/ω）+

γ-R1+γ3（2nπ/ω）=30（4）

下面对系统进行解耦，得到其周期解的表达式.方程（2）可以表示成如下形式：

M+C+Kx=Fsin（ωt+τ），

3=l.（5）

式中：M=[1 0；0 m]，C=2ζK，F=[1；0]，

K=[1+k -k；-k k].

令Ψ表示方程（5）的正则模态矩阵，ω1，ω2表示系统的固有频率，经坐标变换得：

x=Ψξ，ξ=[ξ1 ξ2]T，（6）

将（6）式代入（5）式，解耦得：

[I]+2ζ[Λ]+[Λ]ξ=sin（ωt+τ），

3=-l.（7）

式中：2ζΛ=diag[2ζω21，2ζω22]，=ΨTF，

Λ=diag[ω21，ω22].

由模态叠加法可得方程（7）的通解：

xi=∑2j=1Ψij（e-ηjt（ajcosωdjt+bjsinωdjt）+

Ajsin（ωt+τ）+Bjcos（ωt+τ）），

i=∑2j=1Ψij（e-ηjt（（bjωdjt-ηjaj）cosωdjt-

（ηjbj+ajωdj）sinωdjt）+ωAjcos（ωt+τ）-

Bjω（sin（ωt+τ）），（i=1，2），

x3=C2+C1t-l2t2，

3=C1-lt.（8）

式中：Ψij是正则模态矩阵Ψ的元素；

ηj=ζω2j，ωdj=ω2j-η2j；aj，bj是积分常数，由系统的初始条件和模态参数确定；Aj，Bj是振幅常数：

Aj=ω2j-ω2（ω2j-ω2）2+（2ηjω）2j，

Bj=-2ηjω（ω2j-ω2）2+（2ηjω）2j.（9）

這里j=∑2k=1Ψkjfk0，f10=F1，f20=0.

选择以下截面：

∑={（x1，1，x2，2，x3，3，θ）∈R6×

S1|x1=x3，1=1+，3=3+}，

作为系统的Poincaré截面，其中θ=ωtmod（2π），则X*=（x10，10，x20，20，30，τ）T

表示系统在Poincaré 截面上的周期不动点.参考文献[7]可建立Poincaré 映射：

Xk+1=f（μ，X*）（10）

式中：μ=（ζ，ω）为分岔参数.

Poincaré 映射（10）在不动点X*处的线性化矩阵为：

Df（μ，X*）=f（σμ，ΔX）ΔX|（μ，X*），（11）endprint

式中：ΔX为X的扰动矢量.

2 系统的双Hopf分岔反控制

2.1 反馈控制系统

对系统（2）施加线性反馈控制器：

M+C+Kx+β（-p）+

α（x-xp）=Fsin（ωt+τ），

3=-l（12）

1-+γ3-=1++γ3+，

1+-3+=-R（1--3-）（13）

式中：α和β是线性反馈控制增益矩阵.由于该控制方法并不改变原系统的周期解，所以xp=（x1p，x2p）T和p=（1p，2p）T仍然是原系统的周期解位移和速度.令y=x-xp，=-p，则（12）式可化为：

M*+C*+K*y=

F（sin（ωt+τ）-sin（ωt+τ0））（14）

式中：M*=M，C*=C+β，K*=K+α通过适当的变换可以得到（12）式的通解：

xi=∑2j=1Φij{（e-jt（jcosdjt+jsindjt）+

j[sin（ωt+τ）-sin（ωt+τ0）]+

j[cos（ωt+τ）-cos（ωt+τ0）]}+xip，

i=∑2j=1Φij{（e-jt[（jdjt-jj）cosdjt-

（jj+jdj）sindjt）]+

jω[cos（ωt+τ）-cos（ωt+τ0）]-

jω[sin（ωt+τ）-sin（ωt+τ0）]}+ip，

x3=C4+C3t-l2t2，

3=C3-lt.（15）

式中：Φij是方程（14）的正則模态矩阵；j=ζ2j，dj=2j-2j，j是受控系统的固有频率；j，j，C3，C4，τ是积分常数，由系统的初始条件和周期性条件确定；j，j是振幅常数，由下式求出：

j=2j-ω2（2j-ω2）2+（2jω）2j，

j=-2jω（2j-ω2）2+（2jω）2j，

j=∑2k=1Φkjfk0.（16）

2.2 受控系统的Poincaré 映射

因为该反馈控制方法并不改变原系统的周期解，故选择Poincaré 截面：

σ′={（x1，1，x2，2，x3，3，θ）∈R6×

S|x1=x3，1=1+，3=3+}，

式中：θ=ωtmod（2π）；S=Rmod（2π）；R表示实数.基于原周期解可以建立Poincaré 映射为：

X′k+1=H（μ，ε，Xk），（17）

式中：Xk=（x1k，1k，x2k，2k，3k，τk）T，μ和ε=（k1，k2）分别是分岔参数和控制参数.

2.3 受控系统产生双Hopf分岔的显式临界条件

传统分岔的临界准则，需要在参数空间内逐点取值以求出特征值并验证该特征值是否满足分岔的临界准则，以此来确定控制参数，这样既盲目、具有不确定性又需要计算很长时间.而通过极点配置方法获得的控制参数，其对于控制参数的物理意义、控制鲁棒性和横截条件存在机理不明确问题.所以，本文参考文献[12]推导出不直接依赖于特征值计算的发生双Hopf分岔的显式临界条件，以获得符合条件的控制参数.

设映射在不动点X*=（x10，10，x20，20，30，τ0）T处的线性化矩阵为：

DXH（μ，ε，X*）=H（μ，ε，X*）X*=Q（μ，ε），（18）

其特征多项式有以下形式：

Pμ（λ）=λ6+m1λ5+m2λ4+m3λ3+m4λ2+m5λ+m6，（19）

式中：mi=mi（μ，ε）是与分岔参数μ和控制参数ε有关的实数.

若映射（17）的雅可比矩阵的特征多项式（19）在分岔点处满足如下条件：

（T1） 特征值条件

Pμ0（-1）>0，Pu0（1）>0，

Δ±n-1（μ0）=0，Δ±n-3（μ0）=0，

Δ±j（μ0）>0，

（j=n-2，n-4，…，1（or 2））

（T2）横截条件

2Δ（μ）dμ2μ=μ0≠0，

（T3） 非共振条件

cos（2π/m）≠ψ，ψ=1-Pμ0（1）Δ-32Δ+4，

m=3，4，5，…，

式中：Pμ0（λ），Δ±j（μ0）的具体含义和表达式可参考文献[12].

则映射在分岔点处发生非共振的双Hopf分岔.则可得双Hopf分岔的显式临界条件（具体条件可参考文献[11]）：

1-m6-m4+m6m4+m1m5+m2m6-

m25-m26-m6+m21-m2m26+m6m1m5=0，（20a）

1-m2m1-m3m2-m4m3-m5m4-m6

-m31-m4m1-m5m2-m6m3

-m4-m51-m6m1m2

-m5-m601m1

-m60001=0.（20b）

3 振动筛系统的数值模拟

3.1 原系统的数值模拟

选取振动筛系统的一组参数为：

m=0.18，c=k=0.182，ζ=0.01，

R=064，l=0784，γ=0.16.

使用模态叠加法解耦得到系统的解析解以后直接编程计算，可得质块M1的速度1随着ω变化的分岔图如图2所示：

由图2可以看到系统随着ω的减小发生了分岔，通过MATLAB求得精确分岔点是ω=4.911 1，这里探究分岔点ω=4.911 1附近的动力学行为.endprint

通过计算可以得到该系统线性化矩阵的六个特征值分别为：

λ1，2=0.530 0±0.840 9i，λ3，4=0.031 9±

0.099 94i，

λ5，6=-0.465 8±0.418 3i，

其中|λ1，2|=0.994 0，|λ3，4|=1.000 0，|λ5，6|=0626 0，

可以看出有一對复共轭特征值位于单位圆上，系统发生Hopf分岔，形成拟周期碰振运动.在分岔点ω=4.911 1处原系统的相平面图如图3所示，对应的映射图如图4所示.

当ω=4.9111时，映射图为一吸引不变圈，通过观察这两个图可以看出，质块M1最终趋于稳定的拟周期运动.

3.2 受控系统双Hopf分岔的反控制

选取线性反馈增益矩阵为

α=[k1 -k2；-k2 k1]，β=2ζα，

式中：k1和k2是控制参数.则由以上显式临界条件可以得到控制参数分岔图，如图5所示.

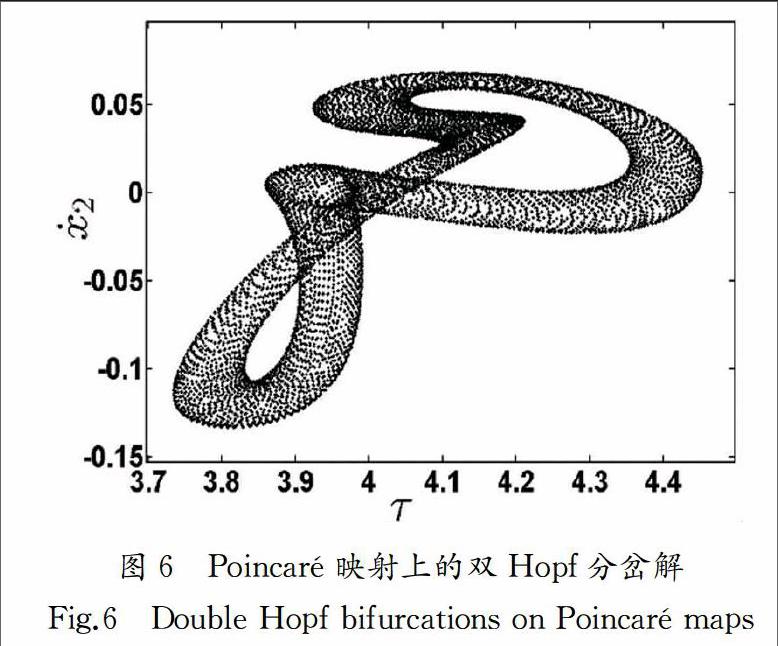
图5中被黑色的粗实线围成的白色区域里的点可以满足条件中的每个不等式，白色区域里的两条细黑实线是由（20a）和（20b）两个等式得到的，通过MATLAB计算出两条直线的交点，取其中一个交点为（0.835 9，0.668 67），在交点附近取一对控制参数（0.937，0.758 76），在该控制增益参数下可得列图6.

可以看出在该控制参数下，映射图6呈现出了“轮胎型”概周期吸引子，得到了原系统的双Hopf分岔解.

以上对分岔点处的动力学进行了分析和分岔反控制，接下来看非分岔点处的分岔反控制效果，在其它系统参数不变的情况下，取ω=4.96同样可以得到6个特征值：

λ1，2=0.538 4±0.835 5i，λ3，4=0.047 5±

0.998 04i，

λ5，6=-0.466 0±0.419 1i，

其中|λ1，2|=0.994 0，|λ3，4|=0.999 1，|λ5，6|=0626 8，可以看出特征值都在单位圆内，原系统处于稳定的周期运动，如图7和图8所示.

同样可得控制参数分岔图，如图9所示.

通过MATLAB计算出两个等式（20a）和（20b）的交点，在其中一个交点附近取一对控制参数（0876 3，0.698 8），在该控制增益参数下可得到图10.

由图可以看出，无论是在分岔点处还是非分岔点处，都可以得到原系统的双Hopf分岔解，同时也体现了显式分岔临界准则的优越性和普适性.

4 结 论

本文建立了振动筛的力学模型，得到分段系统的周期解表达式.通过建立Poincaré 映射，得到映射在不动点处的线性化矩阵，通过分析可知该系统发生了Hopf分岔.然后应用分岔的显式临界准则对原系统进行了双Hopf分岔反控制的分析，通过调节控制增益得到了双Hopf分岔解.该方法的优点就是可以不需要直接计算系统雅克比矩阵的特征值.这一理论结果有助于今后对多自由度振动筛系统的优化设计，也有利于提高振动筛系统的筛分效率，具有一定的实际意义.

参考文献

[1] 吕高常.大型高频振动筛动态特性分析[J].矿山机械，2016，44（6）：58-61.

L Gaochang.Dynamic characteristics analysis on large high-frequency vibrating screen[J].Mining & Processing Equi-pment，2016，44（6）：58-61.（In Chinese）

[2] 赵环帅.大型高频振动筛动态特性及内部应力分布特点分析[J].矿山研究与开发，2013，33（5）：85-89.

ZHAO Huanshuai.Analysis on dynamic behavior and internal stress distribution of large high frequency vibrating screen[J].Mining Research & Development，2013，33（5）：85-89.（In Chinese）

[3] 张则荣，樊智敏，王永岩.大型直线振动筛的疲劳寿命及可靠性分析[J].煤炭学报，2014，39（S1）：257-261.

ZHANG Zerong，FAN Zhimin，WANG Yongyan.Fatigue life and reliability analysis of large linear vibrating screen[J].Journal of China Coal Society，2014，39（S1）：257-261.（In Chinese）

[4] 孙旖.大型振动筛的可靠性研究与应用[J] .矿山机械，2016，44（11）：54-58.

SUN Yi.Reliability study and application of large-scale vibrating screen[J].Mining & Processing Equipment， 2016，44（11）：54-58.（In Chinese）

[5] 陈会征，陈予恕.振动筛分机械相关问题的研究进展[C]//中国力学学会.第十三届全国非线性振动暨第十届全国非线性动力学和运动稳定性学术会议摘要集.中国天津，2011：870-876.

CHEN Huizheng，CHEN Yushu.Research progress of vibration screening machinery related problems[C]// Chinese Society of Mechanics.Thirteenth National Symposium on Nonlinear Vibration and the 10th National Conference on Nonlinear Dynamics and Motion Stability.Tianjing，China，2011：870-876.（In Chinese）endprint

[6] 白亮亮，李万祥，沙世民.直线筛分机系统的非线性响应分析[J] .科学技术与工程，2015，15（35）：36-41.

BAI Liangliang，LI Wanxiang，SHA Shimin.Nonlinear response analysis of linear screening system[J].Science Technology and Engineering，2015，15（35）：36-41.（In Chinese）

[7] 張永祥，孔贵芹，俞建宁.振动筛系统的两类余维三分岔与非常规混沌演化[J].物理学报，2008，57（10）：6182-6187.

ZHANG Yongxiang，KONG Guiqin，YU Jianning.Two codimension -3 bifurcation and non-typical routes to chaos of a shaker system[J].Acta Physica Sinica，2008，57（10）：6182-6187.（In Chinese）

[8] CHEN Z，YU P.Controlling and anti-controlling Hopf bifurcations in discrete maps using polynomial functions[J].Chaos Soltions & Fractals，2005，26（4）：1231-1248.

[9] 刘素华，唐驾时.四维Qi系统零平衡点的Hopf 分岔反控制[J].物理学报，2008，57（10）：6162-6168.

LIU Suhua，TANG Jiashi.Anti-control of Hopf bifurcation at zero equilibrium of 4D Qi system[J].Acta Physica Sinica，2008，57（10）：6162-6168.（In Chinese）

[10]CHENG Z S.Anti-control of Hopf bifurcation for Chens system through washout filters[J].Neurocomputing，2010，73（16）：3139-3146.

[11]伍新，文桂林，徐慧东，等.惯性式冲击振动落砂机周期倍化分岔的反控制[J].固体力学学报，2015，36（1）：28-34.

WU Xin，WEN Guilin，XU Huidong，et al.Anticontrolling period-doubling bifurcation of an inertial impact shaker system[J].Chinese Journal of Solid Mechanics，2015，36（1）.：28-34.（In Chinese）

[12]伍新，文桂林，何丽萍，等.振动落砂机系统的拟周期碰撞设计[J].湖南大学学报：自然科学版，2016，43（4）：38-43.

WU Xin，WEN Guilin，HE Liping，et al.Design of quasi-periodic impact motion of an impact shaker system[J].Journal of Hunan University： Natural Sciences，2016，43（4）：38-43.（In Chinese）

[13]徐慧东，文桂林，伍新，等.三自由度含间隙碰撞振动系统Poincaré 映射 Hopf-Hopf交互分岔的反控制[J].振动工程学报，2015，28（6）：952-959.

XU Huidong，WEN Guilin，WU Xin，et al.Anti-controlling Hopf-Hopf interaction bifurcation on Poincaré map of a three-degree-of-fredom vibro-impact system with clearance[J].Journal of Vibration Enginering，2015，28（6）：952-959.（In Chinese）

[14]WEN G L，CHEN S J，JIM Q T.A new criterion of period-doubling bifurcation in maps and its application to an inertial impact shaker[J].Journal of Sound and Vibration，2008，311（1）：212-223.

[15]伍新，文桂林，徐慧东，等.三自由度含间隙碰撞振动系统Neimark-Sacker分岔的反控制[J].物理学报，2015，64（20）：93-100.

WU Xin，WEN Guilin，XU Huidong，et al.Anti-controlling Neimark-Sacker bifurcation of a three-degree-of-fredom vibration system with clearan-ce[J].Acta Physica Sinica，2015，64（20）：93-100.（In Chinese）endprint