三维全五向编织复合材料的切边效应

刘振国， 黄祥， 亚纪轩， 雷冰， 李小康, 程新

1.北京航空航天大学 航空科学与工程学院， 北京 100083 2.西安航天复合材料研究所， 西安 710025

三维全五向编织复合材料的切边效应

刘振国1,*， 黄祥1， 亚纪轩1， 雷冰1， 李小康1, 程新2

1.北京航空航天大学 航空科学与工程学院， 北京 100083 2.西安航天复合材料研究所， 西安 710025

对切割与未切割的三维全五向(3DF5D)编织复合材料进行了纵向拉伸力学性能研究。首先分别对2种编织角下3种不同情况(未切割、沿厚度方向切边和沿宽度方向切边)的试件进行了力学性能实验，实验结果表明，沿着厚度方向切边使材料的刚度和强度分别下降了约10%和25%；沿着宽度方向切边使材料刚度和强度分别下降了约3%和18%；进一步通过有限元数值模拟对上述实验过程进行了仿真计算，得到了单胞的损伤演化过程、破坏机理以及应力-应变曲线。最后对实验结果和计算结果进行了对比，结果显示二者吻合良好。研究结果表明，三维全五向编织复合材料的编织角越大，拉伸刚度和强度会越小；试件尺寸越大，厚度方向和宽度方向切边的影响越小，并趋于定值。

三维全五向； 编织角； 切边效应； 实验研究； 力学性能

三维编织复合材料是近年来逐渐发展起来的一种新型先进复合材料，具有良好的整体性与可设计性，与传统的层合复合材料相比有着独特优越的力学性能，克服了层合板易分层、抗冲击性能差的缺点[1-2]。常规复合材料是把预浸料按一定角度与顺序进行铺叠或者把纤维束或丝缠绕制成的，纤维形成典型的二维结构。三维编织复合材料是通过纤维束相互交织形成预制件，然后经过固化成型而最终得到的[3]。根据纤维的空间走向特征，可分为三维四向、五向和多向等，其中三维全五向(3DF5D)编织复合材料在内部细观结构上比三维五向编织复合材料轴向纱总数提高了1倍，同时改善了编织纱和轴向纱的直线度，明显增强了该材料的轴向性能[4]。但三维编织复合材料在工程应用中会进行相应的机械加工，且在特定的工作环境下也会发生磨损与烧蚀，对材料的表面纤维结构造成一定的破坏，降低结构的承载能力。

Lu等[5-6]研究了一种针对三维四向编织复合材料的六边形截面纤维束结构单胞模型，并采用有限元方法计算了其弹性模量。Zhang等[7]研究了三维全五向编织复合材料并建立相应的胞元模型，对模型进行了有限元刚度预测，为后续的三维全五向编织复合材料研究奠定了基础。Zeng等[8]研究了单胞内的纤维束和基体的应力分布，并在此基础上对三维编织复合材料失效破坏的全过程非线性应力应变响应进行了模拟，其数值仿真结果与实验结果对比具有较好的一致性。卢子兴和刘振国[9]研究了三维编织复合材料的刚度性能有限元分析模型，对单胞内纤维纱束和树脂基体局部单元细观应力进行计算，初步建立了一个基于经验数据的材料宏观失效准则。Fang等[10-12]建立了八边形纤维束截面的三维四向编织复合材料的几何单胞模型，然后对单胞中的纤维束、基体与界面分别引入相应的初始损伤准则并区分材料不同的破坏模式，对三维四向编织复合材料在单轴拉伸与压缩载荷条件下的渐近损伤演化过程进行了仿真分析。

Macander等[13]研究了切边和未切边三维编织复合材料试件的力学性能。实验结果显示三维四向和五向编织复合材料件的平均拉伸强度分别较未切边的试件下降了将近60%和50%。陈绍杰和梁晶红[14]研究了切割对三维编织复合材料的性能影响，切割后强度下降了接近50%。Li等[15]研究了切割三维四向编织复合材料厚度方向和宽度方向上拉伸、压缩和弯曲的实验对比，由实验得出，宽度方向切割相对厚度方向切割来说，对强度和刚度的影响更小。魏丽梅[16]研究了切边对在单一轴向载荷下沿编织方向的三维编织复合材料实验基础力学性能的影响。实验结果显示，较大编织角的未切边试件的拉伸模量、压缩模量和弯曲模量值比较小编织角的试件分别低约60%、65%和48%。编织角对切边与未切边试件的力学性能均有较大的影响。

目前对三维编织复合材料切边损伤的研究还不完善，仅对三维四向编织复合材料切边做了较为系统的实验研究，尚缺乏对三维全五向编织复合材料切边的理论和实验方面的系统研究。而已有研究表明三维全五向编织方式下复合材料的细观结构更为完善，综合性能更好[17]，而对其切边性能的影响研究，将有利于该材料的推广应用。

本文首先通过对周期性单胞模型施加切边状态下的周期性边界条件[18-23]，将损伤力学和断裂力学的理论引入到单胞力学性能分析中，分别对三维全五向单个单胞及多个单胞组合进行有限元仿真并得到其损伤与破坏过程，从而揭示分析其破坏机理，并进一步得到不同尺寸试件对切边影响的变化规律。最后对三维全五向编织复合材料试件进行纵向拉伸实验，分别比较未切边、沿宽度方向切边和沿厚度方向切边3种情况下力学性能的差异，最终通过对比分析仿真结果和实验结果，验证本文分析方法的合理性和结果的准确性。

1 实验研究

1.1 实验准备

本研究中试件由北京柏瑞鼎科技有限公司提供，所用的三维全五向编织复合材料预成形体采用东丽T700-12K碳纤维应用旋转法三维编织机编织而成，所得的预成形体内的纤维细观结构与传统的四步法工艺完全相同，然后以TDE-85环氧树脂为基体，经树脂传递模塑(Resin Transfer Molding， RTM)工艺固化成型。实验用的试件纤维体积含量均为52%左右，分为3种不同情况(未切边、沿厚度方向切边和沿宽度方向切边)，均包括20° 和40° 两种编织角。各种试件的加工方式如图1所示。

切边方式中U表示不进行切割处理；A为沿厚度方向切两面；B为沿宽度方向切两边。如图1所示,切割厚度参照张超等[24]所提出的一个面胞厚度。

表1为切割后各类试件的尺寸，其中每个种类都有3个试件进行对比参照。图2为方式U和方式A两种编织复合材料试件的表面形貌，从图2 中可以清晰地看到纱束被切断。

图1 切边示意图Fig.1 Schematic diagram of cutting edges

表1 各类试件的尺寸参数以及编号

Table1Dimensionparameterandserialnumberofspecimens

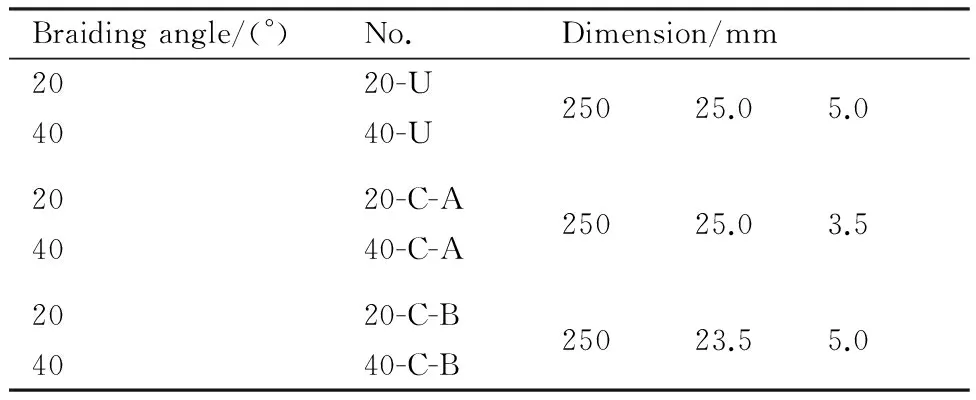
Braidingangle/(°)No.Dimension/mm2020-U4040-U25025.05.02020-C-A4040-C-A25025.03.52020-C-B4040-C-B25023.55.0

图2 方式U和方式A的试件表面Fig.2 Specimen surface of Models U and A

1.2 实验结果

本实验在北京航空航天大学飞行器结构力学实验室的WDW-200E万能试验机上进行，试验机的最大量程为200 kN，在试验过程中，环境温度为20～25 ℃，相对湿度为(46±5)%。拉伸试验参照国家标准GB/T 1447—2005《纤维增强塑料拉伸性能试验方法》[25]实施。

三维全五向编织各类试件纵向拉伸刚度和强度平均计算结果列于表2。表2中的数据显示20-C-A和20-C-B的刚度比20-U分别下降了8.6% 和3.34%，强度分别下降了32.32%和19.48%；40-C-A和40-C-B的刚度比40-U分别下降了10.87%和5.33%，强度分别下降了19.09% 和11.73%。无论对于切边还是未切边的试件，刚度与强度均随着编织角的增大而减小。

图3为三维全五向编织复合材料在3种不同情况下试件的破坏断口图片。由图3中可见，未切割试件的断口平齐，轴向纱全部被沿纵向拉断。编织角为20° 时，轴向纱与编织纱几乎完全是齐根而断，拉伸损伤占主导；编织角为40°时，可以明显地看到纤维束存在横向的破坏，而且存在编织纱被抽拔出的现象。

沿厚度方向切割对三维编织复合材料的拉伸模量与强度有很大的影响。轴向纱与编织纱或者是编织纱与编织纱之间发生了界面脱粘，由于全五向编织复合材料大量轴向纱的存在，试件仍能承受较大的载荷，最终大量轴向纱的破坏导致释放巨大的能量，使得试件断口呈现出爆炸式的蓬松。这是因为切割对纤维的连续性造成了损伤，在受拉伸载荷时，被切割区域附近的纤维束不会发生破坏，而纤维束之间的界面会发生脱粘，在破坏前全部保持很好的线性，表现为脆性断裂。

表2切边后纵向拉伸性能测试平均结果

Table2Averageresultsoflongitudinaltensiletrialaftercut-edge

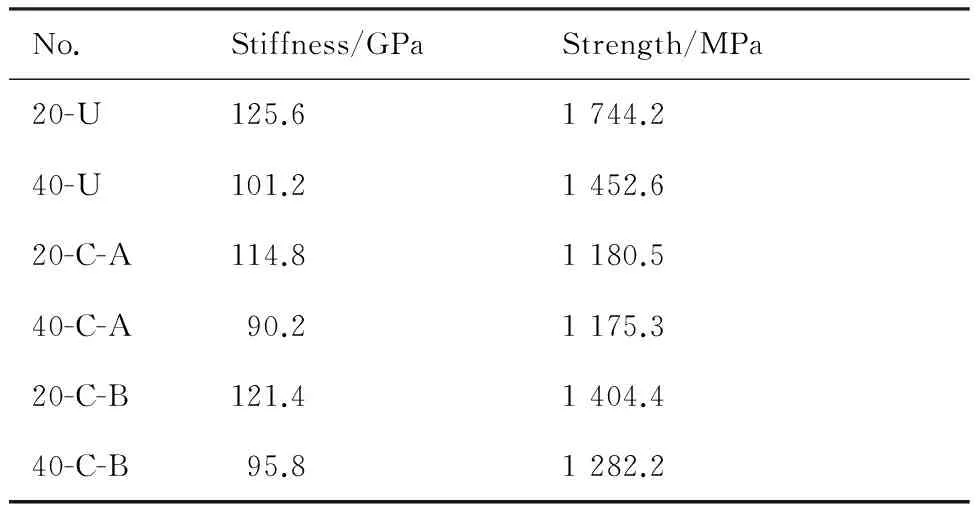
No.Stiffness/GPaStrength/MPa20-U125.61744.240-U101.21452.620-C-A114.81180.540-C-A 90.21175.320-C-B121.41404.440-C-B 95.81282.2

图3 试件破坏断口图片Fig.3 Image of destruction of specimen

沿宽度方向切割时，对三维编织复合材料性能影响不大，虽然试件在两边被切断，但是纤维在其他两个方向上还具有很强的连续性。所以在试件的两边会发现由于纤维切断引起的界面脱粘导致的纤维束被抽拔出来的现象，但是在试件中间断口基本是平齐的。

2 数值模拟

2.1 几何单胞建模

由于三维全五向编织复合材料内部细观结构呈周期性，在此，根据实验观察结果，参考现有的三维编织复合材料内部单胞几何模型进行建模[26-27]，通过给定纱线的基本参数以及编织角，可以在CATIA中构建出三维全五向单胞的几何模型，如图4所示，单胞模型由编织纱、轴向纱与树脂3部分构成。

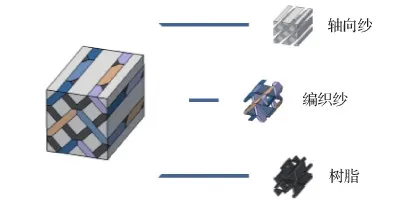
图4 三维全五向编织复合材料的几何单胞模型 Fig.4 Periodic repeated cell model of 3DF5D braided composites

2.2 周期性边界条件

在对单胞进行计算时，需合理地施加周期性边界条件才能准确地计算材料的细观材料性能，图5为切边方向和单元胞体示意图,其中T和N分别表示单胞的厚度方向和宽度方向。

对于未切割的三维编织复合材料的损伤演化模拟分析，由于其在X、Y、Z这3个方向上都具有周期性，所以在单胞的3个对面都施加相应的边界条件，如式(1)所示。

(1)

式中：U、V、W分别为X、Y、Z这3个方向上的位移分量。

图5 切边方向和单元胞体示意图Fig.5 Schematic diagram of cutting direction and unit cell

对于切割后的试件，材料内单胞的周期性受到破坏，在材料内部Y方向上胞体不具有周期性，X与Z方向上仍然具备周期性，所以在施加边界条件时只需要对具有周期性的两个对面：BCGF与ADHE、ABCD与EFGH，施加周期性边界条件,如式(2)所示。

(2)

2.3 纤维束损伤模型

编织结构中的纱束一般可以看做是单向加强的横观各向同性材料，纤维束的破坏准则采用Hashin[28]三维空间应力破坏准则(L、T、Z方向如图6 所示)。

纵向(L方向)拉伸破坏：

(3)

(4)

式中：DL、DT和DZ为纤维纱束3个材料主方向上的损伤状态变量；ni为损伤张量的主方向矢量；⊗为不同主方向上矢量的张量积。

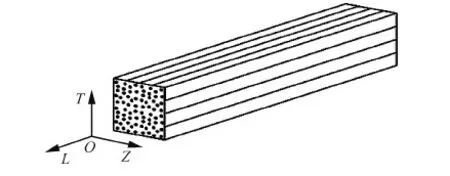
图6 纤维束的L、 T、Z坐标方向Fig.6 L, T, Z coordinate directions of fiber bundle

引入损伤状态变量之后，材料在产生损伤之后的有效应力张量σ*就可以通过弹性应力张量σ表示出来，即

M(D)∶σ

(5)

式中：I为3阶单位张量；σ为弹性应力张量；M(D)为依赖损伤张量D的损伤效应因子。

纤维束3个方向上损伤变量的主值为

(6)

式中：dLt、dTt和dZt分别为L、T和Z方向上的纵向损伤变量；dLc、dTc和dZc分别为L、T和Z方向上的横向损伤变量。

2.4 树脂损伤模型

树脂基体为各向同性材料，对其采用理想的弹塑性本构模型，当应力达到树脂基体的屈服破坏应力σm后，不需要增加任何载荷，变形就能自由增加。

对于树脂基体的屈服准则采用von Mises准则，其具体形式为

(7)

式中：σ1、σ2和σ3分别为X、Y和Z方向上的应力；τ12、τ23和τ31分别为XY、YZ和ZX方向上的切应力。

当树脂发生塑性破坏后，其刚度降为0。

2.5 界面损伤模型

为了考虑纱线基体界面相性能对三维全五向编织复合材料整体力学行为的影响，引入界面相单元COHESIVE，单元编号为COH3D6，这种界面单元的力学性能根据Traction-Separation界面层理论来描述。

在线弹性阶段界面层本构关系可以表示为

(8)

式中：tn、tt、ts为三维界面单元的法向应力与2个切向的剪应力分量；δn、δt、δs为3个方向的位移分量；Knn、Ktt、Kss分别为界面层法向和2个切向的刚度系数。

界面选取二次应力准则作为界面初始损伤准则，即

(9)

式中:σn、σs和σt分别为法向和2个切向的应力分量；N、Ss、St为界面法向强度与2个方向的切向强度，且

(10)

同纤维纱束和基体的损伤演化模式类似，应力达到初始破坏准则之后，界面刚度性能开始进入退化状态，其具体损伤刚度矩阵可以表示为

K(d)=

(11)

式中：dc为引入的界面损伤状态变量。

模型中纤维纱束和固化树脂材料分别为T700-12K碳纤维和TDE-85环氧树脂，纤维和树脂的材料性能如表3所示。

表3T700-12K碳纤维和TDE-85环氧树脂的力学性能

Table3MechanicalpropertiesofT700-12KcarbonfiberandTDE-85epoxyresin

ParameterofcarbonfiberValueParameterofresinValueLongitudinaltensilestiffness/GPa230Stiffness/GPa3.5Transversetensilestiffness/GPa40Strength/MPa80Poissonratio0.26Poissonratio0.35Longitudinalshearstiffness/GPa24Transverseshearstiffness/GPa14.3Longitudinaltensilestrength/MPa4900

2.6 纵向拉伸应力应变

通过采用数值模拟仿真，得到单胞的应力-应变曲线和纵向拉伸应力应变云图。

编织角为20° 和40° 时，试件在拉伸载荷下的应力-应变曲线如图7所示(SIM为仿真结果，EXP为实验结果)。

编织角为20° 时，未切割的三维全五向编织复合材料试件在拉伸载荷下的损伤演化过程如图8 所示。

图7 试件拉伸应力-应变曲线Fig.7 Tensile stress-strain curves of specimens

观察未切边试件实验断口图片，可知损伤和破坏的原因是轴向纱主要承担着纵向载荷，在应变较小时，轴向纱损伤区域并不大，随着应变的增加，轴向纱的纵向损伤逐渐扩展；编织纱的纵向损伤产生于应变ε=1.09%处，主要位于编织纱交错接触区域的附近，随着应力的增加损伤区域沿着编织纱与轴向纱的接触面拓展，最终编织纱的主要纵向损伤区域与轴向纱的损伤严重区域连通在一起。编织纱的横向损伤与轴向纱的横向损伤拓展规律类似，主要出现在编织纱纵向损伤区域；对界面破坏而言，界面结合良好，破坏区域不大。对比实验断口图片也可以看到，试件断口平齐，几乎没有纤维束被拔出。

编织角为20° 时，在拉伸载荷作用下，三维全五向编织复合材料试件沿厚度方向切边时(20-C-A 模型)的损伤演化过程如图9所示。

编织角为20° 时，轴向纱在靠近被切割表面处出现纵向损伤，随着应变的增加，损伤先在被切割表面区域拓展，然后向模型的内部延伸，轴向纱首先出现纵向损伤，随后发生了横向损伤；编织纱的纵向损伤产生在切割表面处，随着载荷的增加，表面处的损伤向模型内部拓展；对于界面的损伤，出现得较早，产生在被切割的两个表面处而且处于两个编织纱交错接触位置的附近，随着应力的增加，该处的损伤缓慢地向单胞内部界面拓展，而且内部编织纱交错位置处的界面也会发生损伤。对比实验断口图片，断口呈现炸开状，看不到明显的断口，而且大量的界面发生脱粘，最后轴向纱产生纵向破坏导致试件的断裂。

在编织角为20° 沿宽度方向切边时(20-C-B模型)，三维全五向编织复合材料试件在宽度方向上为多个内胞的模型，在拉伸载荷下的损伤演化过程如图10所示。

编织角为20° 时，沿宽度方向切边试件轴向纱的初始损伤位置在切割处，随着载荷的增加，纵向损伤向内部拓展，轴向纱的横向损伤与前2种情况类似，出现在已发生纵向损伤的区域；编织纱的损伤区域出现在轴向纱损伤位置附近的切割处，随着应力增加编织纱沿轴向纱损伤区域拓展，编织纱的轴向损伤产生于纵向损伤之后；界面损伤出现较早，位于切割处编织纱相互交错位置处，随着应力的增加其损伤拓展缓慢，当轴向纱与编织纱出现损伤后，与其接触的界面会迅速产生损伤，而且沿着编织纱与轴向纱损伤区域迅速拓展。实验断口图片显示试件两边的轴向纱与编织纱散开，界面发生脱粘，试件中部的断口平齐，说明轴向纱与编织纱由于拉伸载荷而发生破坏，仿真结果与实验结果吻合得较好。

三维全五向编织仿真结果与实验结果的比较如表4所示。由表4可以看出，数值仿真结果与实验结果的最大偏差在10%以内，较为吻合，初步验证了三维全五向编织复合材料细观强度计算方法的正确性。

分析结果表明：轴向纱纵向的损伤演化形式起到了决定性的作用；对于编织纱而言，编织角较小时，编织纱的损伤主要为纵向损伤，编织角较大时，横向损伤逐渐占主要地位；对于未切割的情况，随着编织角的增大，纱线之间界面的应力水平不断提高，因此大编织角的界面损伤失效面积相对于小编织角情况显著增加；对于进行切割后的情况，界面与树脂的损伤首先产生于被切割位置，随着应变的增加，界面的损伤会逐渐向模型内部拓展。

Note: LDF——Longitudinal Damage Factor.图8 20° 编织角未切边试件的损伤演化过程图Fig.8 Damage evolution of uncut-edge sample under 20° braiding angle

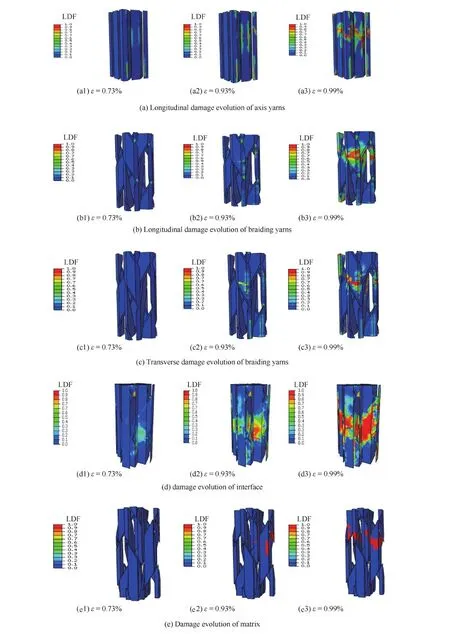
图9 20° 编织角沿厚度方向切边后的损伤演化图Fig.9 Damage evolution of 20-C-A model

图10 20° 编织角沿宽度方向切边后的损伤演化图Fig.10 Damage evolution of 20-C-B model

表4 仿真结果与实验结果比较Table 4 Comparison of simulation and experiment results

No.Stiffness/GPaExperimentSimulationStiffnessrelativeerror/%Strength/MPaExperimentSimulationStrengthrelativeerror/%20-U125.6130.54.01744.21621.37.120-C-A114.8116.21.81180.51078.88.620-C-B121.4126.85.01404.41341.24.640-U101.2 98.33.01452.61421.72.140-C-A 90.2 96.24.41175.31134.63.440-C-B 95.8 97.32.11282.21195.26.8

未切边与切边后编织结构主要区别为：未切边编织结构表面由面胞组成，面胞纱束连续，载荷可以有效传递；切边后对编织结构造成了损伤，载荷无法通过表面进行传递，因此承载能力大大下降。

2.7 多单胞情况下的仿真

由于在上文中已经验证了在仅有一个单胞情况下仿真结果的正确性，为了模拟和说明实际结构件的尺寸对不同切边方式的影响，对厚度比较大的情况进行预测分析，对有1、2、3、6个单胞的情况进行仿真对比，如：20-C-A-2表示编织角为20°、切边方式为沿厚度方向和2个单胞的情况。

以20° 编织角为例，图11为模型有不同数量单胞时，仿真计算得到的试件在拉伸载荷下的应力-应变曲线。

有多个单胞时材料的拉伸强度和刚度如图12 所示。

图11 仿真得到的多单胞材料的应力-应变曲线 Fig.11 Stress-strain curves of multicellular material by simulation

图12 多单胞材料的强度和刚度柱状图 Fig.12 Histograms of stiffness and strength of multicellular materials

根据以上仿真结果可知，对材料切割后，初始时纤维束为轴向纱损伤，随着载荷的增加，损伤从外部向内部拓展。在多单胞情况下，随着内胞个数的增加，切边位置仍在初始缺陷发生的位置，但内胞数所占比例变大，面胞所占材料的比例相对减小，表面损伤对整体性能影响减小，切边后整体纵向性能有所提升。因此可减小面胞所占比例来减小切边对材料性能的影响。

随着结构件尺寸增加，切边效应影响减小，可提出以下建议改善切边影响：采用多向编织来增强材料的切边性能，增大纤维体积含量；增加受力方向上纱线的比例。

3 结 论

做了三维全五向编织复合材料的标准试件切边实验和仿真计算研究，基于实验与仿真的力学性能结果，研究了不同切边方式对三维全五向编织复合材料力学性能的影响。预测了单胞的纵向拉伸模量和极限强度，分析了细观组分损伤失效机理，结论如下：

1) 三维全五向编织复合材料在承受纵向拉伸载荷时，轴向纱的纵向损伤演化形式起到了决定性的作用；编织角较小时，编织纱的损伤主要为纵向损伤，编织角较大时，横向损伤逐渐占主要地位，同时编织角越大，复合材料的拉伸模量和强度越小。

2) 三维全五向编织复合材料在纵向拉伸载荷作用下，纱线之间交错处出现了明显的应力集中现象。同时随着编织角的增大，纱线之间界面的应力水平不断提高。对于进行切割后的情况，界面与树脂的损伤首先产生于被切割位置，随着应变的增加，界面的损伤逐渐向模型内部拓展。

3) 基于单个单胞的仿真方法的正确性，对多单胞(大尺寸)的情况进行了分析，结果显示结构件的尺寸越大，局部切边对于整体性能的影响越小。

4) 对比三维全五向编织复合材料的仿真与实验结果，材料应力-应变曲线的数值模拟结果与实验结果都接近于线性且吻合良好，这说明本文建立的三维全五向编织复合材料模型对于材料渐进损伤失效分析是适用的，具有工程实用价值。

[1] 杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1): 1-12.

DU S Y. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica, 2007, 24(1): 1-12 (in Chinese).

[2] 卢子兴, 杨振宇, 李仲平. 三维编织复合材料力学行为研究进展[J]. 复合材料学报, 2004, 21(2): 1-7.

LU Z X, YANG Z Y, LI Z P. Development of investgation into mechanical behavior of three dimensional braded composites[J]. Acta Materiae Compositae Sinica, 2004, 21(2): 1-7 (in Chinese).

[3] 吴德隆, 沈怀荣. 纺织结构复合材料的力学性能研究[J]. 力学进展, 2001, 31(4): 583-591.

WU D L, SHEN H R. The study of mechanical properties of textile structural composites[J]. Advances in Mechanics, 2001, 31(4): 583-591 (in Chinese).

[4] 刘振国. 三维全五向编织预制件的概念[J]. 材料工程, 2008(S1): 305-312.

LIU Z G. Concept of three-dimentional all five-directionnal braided preforms[J]. Journal of Materials Engineering, 2008(S1): 305-312 (in Chinese).

[5] LU D S, LU J L, CHEN L, et al. Finite element analysis of mechanical properties of 3D four-directional rectangular braided composites Part 1: Microgeometry and 3D finite element model[J]. Applied Composite Materials, 2010, 17(4): 373-387.

[6] LU D S, FANG D N, LU Z X, et al. Finite element analysis of mechanical properties of 3D four-directional rectangular braided composites—Part 2: Validation of the 3D finite element model[J]. Applied Composite Materials, 2010, 17(4): 389-404.

[7] ZHANG F, LIU Z G, WU Z , et al. A new scheme and microstructural model for 3D full 5-directional braided composites[J]. Chinese Journal of Aeronautics, 2010, 23(1): 61-67.

[8] ZENG T, FANG D N, MA L, et al. Predicting the nonlinear response and failure of 3D braided composites[J]. Materials Letters, 2004, 58(26): 3237-3241.

[9] 卢子兴, 刘振国. 三维编织复合材料强度的数值预报[J]. 北京航空航天大学学报, 2002, 28(5): 563-565.

LU Z X, LIU Z G. Numerical prediction of strength for 3D braided composites[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(5): 563-565 (in Chinese).

[10] FANG G D, LIANG J,WANG B L. Progressive damage and nonlinear analysis of 3D four-directional braided composites under unidirectional tension[J]. Composite Structures, 2009, 89(1): 126-133.

[11] FANG G D, LIANG J, WANG Y, et al. The effect of yarn distortion on the mechanical properties of 3D four-directional braided composites[J]. Composites Part A: Applied Science and Manufacturing, 2009, 40(4): 343-350.

[12] FANG G D, LIANG J, WANG B L, et al. Effect of interface properties on mechanical behavior of 3D four-directional braided composites with large braid angle subjected to uniaxial tension[J]. Applied Composite Materials, 2010, 18(5): 449-465.

[13] MACANDER A B, CRANE R M, CAMPONESCHI E T. Fabrication and mechanical properties of multidimensionally (XD) braided composite materials[J]. ASTM STP, 1986, 873: 422-445.

[14] 陈绍杰, 梁晶红. 三维编织复合材料结构的发展与应用[J]. 航空制造工程, 1994(4): 33-35.

CHEN S J, LIANG J H. Development and application of 3D braided composite materials[J]. Aviation Manufacture Engineering, 1994(4): 33-35 (in Chinese).

[15] LI J L, JIAO Y, SUN Y, et al. Experimental investigation of cut-edge effect on mechanical properties of three-dimensional braided composites[J]. Materials and Design, 2007, 28(9): 2417-2424.

[16] 魏丽梅. 切边对三维纺织复合材料力学性能的影响[D]. 天津: 天津工业大学, 2005: 12-19.

WEI L M, The effect of cut-edge on mechanical properties of three-dimensional braiding composites[D]. Tianjin: Tianjin Polytechnic University, 2005: 12-19 (in Chinese).

[17] ZHANG F, LIU Z G, WU Z, et al. A new scheme and microstructural model for 3D full 5-directional braided composites[J]. Chinese Journal of Aeronautics, 2010, 23(1): 61-67.

[18] XIA Z, ZHANG Y, ELLYIN F, et al. A unified periodical boundary conditions for representative volume elements of composites and applications[J]. International Journal of Solids and Structures, 2003, 40(8): 1907-1921.

[19] XIA Z, ZHOU C, YONG Q, et al. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites[J]. International Journal of Solids and Structures, 2006, 43(2): 266-278.

[20] LI S. Boundary conditions for unit cells from periodic microstructures and their implications[J]. Composites Science and Technology, 2008, 68(9): 1962-1974.

[21] HARPER L T, QIAN C, TURNER T A, et al. Representative volume elements for discontinuous carbon fibre composites—Part 1: Boundary conditions[J]. Composites Science and Technology, 2012, 72(2): 225-234.

[22] HARPER L T, QIAN C, TURNER T A, et al. Representative volume elements for discontinuous carbon fibre composites—Part 2: Determining the critical size[J]. Composites Science and Technology, 2012, 72(2): 204-210.

[23] LI S, WONGSTO A. Unit cells for micromechanical analyses of particle-reinforced composites[J]. Mechanics of Materials, 2004, 36(7): 543-572.

[24] 张超, 许希武, 严雪. 三维五向及全五向编织复合材料的三单胞结构模型[J]. 南京航空航天大学学报，2013, 45(2): 171-178.

ZHANG C, XU X W, YAN X. Three unit-cell structure models of 3-D five-directional and full five-directional braided composite[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(2): 171-178 (in Chinese).

[25] 李艳华, 邬友英, 胡中永, 等.纤维增强塑料拉伸性能试验方法: GB/T 1447—2005[S]. 北京: 中国标准出版社, 2005: 1-11.

LI Y H, WU Y Y, HU Z Y, et al. Fiber-reinforced plastic composites—Determination of tensile properties: GB/T 1447—2005[S]. Beijing: Standards Press of China, 2005: 1-11 (in Chinese).

[26] ZHENG X T, YE T Q. Microstructure analysis of 4-step three-dimensional braided composite[J]. Chinese Journal of Aeronautics, 2003, 16(3): 142-150.

[27] LIU Z G, ZHANG H G, LU Z X, et al. Investigation on the thermal conductivity of 3-dimensional and 4-directional braided composites[J]. Chinese Journal of Aeronautics, 2007, 20(4): 327-331.

[28] HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics, 1980, 47(2): 329-334.

(责任编辑： 徐晓)

URL：www.cnki.net/kcms/detail/11.1929.V.20170512.1058.002.html

*Correspondingauthor.E-mail:liuzg@buaa.edu.cn

Cut-edgeeffectofthree-dimensionalfullfive-directionalbraidedcomposites

LIUZhenguo1,*,HUANGXiang1,YAJixuan1,LEIBing1,LIXiaokang1,CHENGXin2

1.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China2.Xi’anAerospaceCompositesResearchInstitute,Xi’an710025,China

Experimentalresearchoncut-edgeanduncut-edgeeffectsofthemechanicalperformanceofthree-DimensionalFullfive-Directional(3DF5D)braidedcompositesisconducted.Thespecimensincludetwodifferentbraidinganglesandthreedifferentcuttingways(uncut-edge,cutalongthethicknessdirectionandcutalongthewidthdirection).Themechanicalperformancesofthespecimensareobtainedandstudiedtogettheconclusionofthecut-edgeinfluence.Itisfoundthatforthespecimencutalongthethicknessdirection,thereisapproximately10%reductioninaveragestiffnessand25%reductioninaveragestrength,comparedwithspecimenswithoutcut-edge;whileforthespecimencutalongthewidthdirection,thestiffnessandstrengthdecreaseby3%and18%,respectively.Theprogressivedamageandfailureprocessofmesoscopicbraidedstructuresareinvestigatedbasedontherepeatedunitcells,andthenthestress-straincurveofthespecimenisobtained.Goodagreementisobtainedbetweenthenumericalandexperimentalresults.Resultsshowthatthetensilestiffnessandstrengthdecreasewiththeincreaseofthebraidingangle.Thecut-edgeeffectontheperformanceoffull5-directionalbraidedcompositesperformanceweakensandcomesclosetoaconstantwiththeincreaseofinnercells.

3DF5D;braidingangle;cut-edgeeffect;experimentalstudy;mechanicalproperty

2016-10-25；Revised2016-11-14；Accepted2017-04-25；Publishedonline2017-05-121058

2016-10-25；退修日期2016-11-14；录用日期2017-04-25； < class="emphasis_bold">网络出版时间

时间：2017-05-121058

www.cnki.net/kcms/detail/11.1929.V.20170512.1058.002.html

.E-mailliuzg@buaa.edu.cn

刘振国, 黄祥, 亚纪轩, 等. 三维全五向编织复合材料的切边效应J. 航空学报,2017,38(8):220885.LIUZG,HUANGX,YAJX,etal.Cut-edgeeffectofthree-dimensionalfullfive-directionalbraidedcompositesJ.ActaAeronauticaetAstronauticaSinica,2017,38(8):220885.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.220885

V258+.3; TB332

A

1000-6893(2017)08-220885-12